《數學分析》課程中融入數學文化的教學策略研究

張玉新，丁恒飛

(天水師范學院 數學與統計學院,甘肅 天水 741001)

從中學跨入大學校門,大多數學生對學習數學感到壓力巨大，學不懂,從而導致學習的積極性不高,甚至產生轉專業,厭學和退學的情況.這是因為大學階段的數學課程學習所需要的方法和思維方式與中學截然不同,跨度很大，其難度有質的飛越.大學階段的數學課程其特點是知識結構與體系完整,推理嚴密.在通常的教學過程中,由于受傳統教學方式，課時及其教師水平與層次,教材編寫和考試考核方式的影響,教師對數學概念的來龍去脈、思想和方法的形成過程以及數學教學中體現數學文化元素成份的內容重視程度不高,只是一味地給學生灌輸數學概念和定理,重點關注理論性的結果.《數學分析》是數學與應用數學專業的專業核心基礎課,是學習《常微分方程》《復變函數》《實變函數》與《泛函分析》等后繼課程的基礎，學生一入學就接觸這門課程,且課程開設的時間最長,一般達到三學期.如果教師能在《數學分析》課程的教學過程中,以數學文化為背景和驅動,穿插一些數學史、數學思想與方法、數學模型等數學文化的元素,可以提高學生學習數學的興趣和課堂教學效果,使學生進一步了解數學的內涵、本質和價值,有助于學生數學技能和人文素質的養成.

1 數學文化的含義

20世紀60年代,美國學者懷爾德[1]首次提出了“數學是一種文化”的觀點,之后在國內外掀起了對數學文化進行討論和研究的熱潮.1980年,紐約大學庫朗數學研究所教授莫里斯·克萊因在《西方文化中的數學》一書自序中寫道：“在西方文明中,數學一直是一種主要的文化力量.幾乎每個人都知道,數學在工程設計中具有極其重要的實用價值.最為重要的是,作為一種寶貴的、無可比擬的人類成就,數學在使人賞心悅目和提供審美價值方面,至少可與其他任何一種文化門類相媲美”[2].2005年,著名的數學家李大潛院士在《大學數學》課程報告論壇上,曾指出：“數學是一種先進的文化,是人類文明的重要基礎.它的產生和發展在人類文明的進程中起著重要的推動作用,占有舉足輕重的地位”[3].隨后,眾多的學者提出了數學文化的含義,如黃秦安先生對數學文化的理解為：“以數學科學為核心, 以數學的思想、精神、方法、內容等所輻射的相關文化領域為有機組成部分的一個具有特定功能的動態系統”[4].南開大學著名學者顧沛老師則對數學文化作了更為詳細的闡述：數學文化是指數學思想、精神、方法、觀點,以及他們的形成和發展.更廣泛地說,除上述內涵外,還包含數學家、數學史、數學美、數學教育、數學發展中的人文成分、數學與社會的聯系、數學與各種文化的關系等等[5].盡管對數學文化的描述和理解不盡相同,但將數學作為一種文化已成為當下數學界同仁達成的共識.

通過以上學者和專家對數學文化的闡述,可以深刻認識到數學文化有廣義與狹義之分.從廣義方面來講, 數學文化指的是數學家、教育家以及在數學發展過程中所有的人文成分,數學同各個文化之間的關系.從狹義方面來講,數學文化就是指數學中所蘊含的思想、精神以及方法[6].相對于數學知識而言,數學文化所包含的內容更加豐富,內涵更加深刻,它是對數學知識與思想,數學能力與素質的高度概括和體現.

2 數學教學中滲透數學文化的重要性

2.1 可以激發學生進取心與愛國情懷

在中學階段,由于高考“指揮棒”的作用,學生的主要目標是高考,高考考什么學生就學習什么,學習往往是被動的.進入大學階段,由于就業等因素的影響,學生對大學數學學習的目標是茫然的,再加上中學數學和大學數學的思維形式不同,出現了學生對學習數學的消極態度.如果在《數學分析》教學中,教師在課堂中適當引入一些著名數學家故事,介紹他們在遇到一些棘手問題時,是如何面對和解決的,這樣可以增強學生克服困難的決心和信心,進一步激發學生學習熱情.比如著名數學家張益唐,他在2013年第一次成功證明了弱版本的孿生素數猜想.張益唐是真的能潛下心來搞科研的人，作出巨大數學貢獻的他已接近60歲,之前只是個默默無聞的講師,為潛心研究數學,他幾乎把自己與世隔絕,他妹妹曾在網上發尋人啟事尋找哥哥.此外,在講數列極限這一節,會提到《莊子——天下篇》中一句話“一尺之錘,日取其半,萬世不竭”[7],這就是極限概念的雛形,可見中國古代思想家的智慧.再進一步聯想到現當代著名數學家陳省身先生,他晚年致力于推進中國數學的發展,在母校南開大學創立了陳省身數學研究所,并于2002年促成了四年一度的國際數學家大會在中國北京召開(系首次在發展中國家召開).陳先生培養了包括廖山濤、吳文俊、丘成桐、鄭紹遠,李偉光等一大批著名的數學家.其中,丘成桐是取得國際數學聯盟菲爾茲獎的第一個華人,也是繼陳省身之后第二個獲沃爾夫獎的華人.通過這些真實的例子可以很好地激發學生的愛國情懷，增強民族自信心.

2.2 可以提高教師自身數學文化素養

“教師要有一桶水,才能給學生一碗水”,這是教育界的一句傳統名言.隨著社會的進步和科技的發展,高等教育也在飛速發展,如果僅僅停留在一碗水與一桶水上,已不能適應社會和高等教育發展的需求.如今的教育,如今的教師,如果只追求“一桶水”,顯然已經不行,現在已經到了“教師要有一桶水,還應指給學生一條河；教師就是一條河,要引導學生奔大海”的這種態勢.教師必須追求和提高自己的專業發展,教師之“水”應該是一條溪流,一條能有泉水不斷補充進來的孜孜不倦的溪流.如果要在教學活動過程中融入數學文化的成分,必須提前對教學內容進行選取,了解哪些數學知識蘊藏豐富的數學文化,哪些數學知識蘊含豐富的數學價值觀,哪些數學知識能夠具備文化傳遞功能,通過這種思考和學習,教師自身的文化素養一定會提高.

2.3 可以培養學生的探索與創新能力

探索和創新能力是民族進步的靈魂、經濟競爭的核心.當今社會的競爭,與其說是人才的競爭,不如說是人的創造力的競爭.在科學技術飛速發展的今天,創新意識和創新能力越來越成為一個國家國際競爭力和國際地位的最重要的決定因素.當代大學生作為人類歷史文化傳承和發揚的主要群體,培養他們的探索精神和創新能力是非常有必要的.比如在《數學分析》課程教學過程中,講到微積分時,適當引入分數階微積分,引導學生會查閱資料,進一步分析它們的異同,可以得到一些有用的結論.再比如講到Gamma函數時,引導學生探索它的一些基本性質及其相關等式,并能做進一步證明,如果能成功證明一些,這樣會增強學生對數學學習的信心,慢慢也會培養學生的探索與創新能力.

3 教學中滲透數學文化的方式與策略

3.1 在課堂中引入相關的數學史知識

《數學分析》課程中數學術語繁多,大多都有相關的歷史背景.比如對于微積分一詞,可以引入它的發展歷程.公元前3世紀,古希臘的數學家、力學家阿基米德在研究解決拋物線下的弓形面積、球和球冠面積、螺線下的面積和旋轉雙曲線所得的體積問題中就隱含著近代積分的思想.公元前7世紀,古希臘科學家、哲學家泰勒斯在對球的面積、體積和長度等問題的研究中也蘊含有微積分思想.中國古代數學家,三國時期的劉徽曾在割圓術及求體積問題的設想中也產生過積分學的萌芽思想.到了17世紀,許多著名的數學家、天文學家、物理學家,如法國的費馬、笛卡爾、羅伯瓦、笛沙格，英國的巴羅、瓦里士，德國的開普勒，意大利的卡瓦列利為解決實際問題需要,也產生了微積分的思想,為微積分的創立做出了貢獻.17世紀下半葉,在前人工作的基礎上,英國數學家和物理學家牛頓與德國數學家萊布尼茨分別獨自完成了微積分的初步創立工作，他們的最大功績是把兩個貌似毫不相關的問題：切線問題(微分學的中心問題)和求積問題(積分學的中心問題)緊密聯系在一起.

歷史上,關于微積分的成果歸屬和優先權問題,曾在數學界引起了一場長時間的大爭論.這場爭論的重要性不在于誰勝誰負的問題,而是使數學家分成兩派.一派是英國數學家,捍衛牛頓；另一派是歐洲大陸數學家,尤其是伯努利兄弟,支持萊布尼茨.兩派相互對立甚至敵對.后經查證表明,雖然牛頓工作的大部分是在萊布尼茲之前做的,但是,萊布尼茲是微積分主要思想的獨立發明人[8].直到19世紀初,法國科學學院的科學家以柯西為首,對微積分的理論進行了認真研究,建立了極限理論.后來又經過德國數學家維爾斯特拉斯進一步地嚴格化,使極限理論成為了微積分的堅定基礎,才使微積分進一步的發展壯大.引入這些數學史知識,不僅提高了學生的學習興趣,也對學生的人文素養的提高大有裨益.

3.2 用數學方法去解決實際問題

在課堂中引入一些實際的問題,嘗試用數學的方法去解決,這樣既可以增強學生的動手能力,又可以激發他們對數學產生濃厚的興趣.比如有這樣一道實際問題：

例1一無人機在海拔高度為3 km的高空,以200 km/h的速度水平飛行到天水南郭寺景區上空進行風景攝影(景區內海拔高度在1.2～1.7 km之間),試求該無人機至景區上空時攝影機轉動的角速度.

在學完函數的導數及其相關變化率之后,問題可以迎刃而解.下面給出詳細過程：假設無人機與景區正上空水平距離為x(km),OA與OB之間的夾角為θ，如圖1所示.

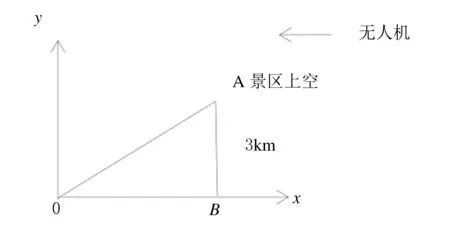
圖1 例1示意圖

則

且角速度為

因此，無人機飛至景區上空時角速度為

3.3 將哲學觀點“特殊與一般”貫穿在課堂

哲學中特殊與一般是相對的概念和范疇,它們具有辯證統一的關系.從唯物主義的角度來講,事物的一般與特殊是客觀存在的,均為現實世界中事物與現象所固有的.從認識論的角度來講,認識任何事物,不僅要認識它的普遍性,同時還要重視其特殊性.實際上,任何事物都是共性與個性的統一體.《數學分析》的教學過程中,教師要充分挖掘課本中蘊含的哲學觀點“特殊與一般”的數學內容,如果能將其貫穿在課堂的過程中,不僅能讓學生加深對數學概念的理解,還能將他們的認識提高到一個更高的層次,拓寬了知識面,也培養了良好的思考習慣.

下面通過兩個例子來說明課堂中如何體現“特殊與一般”這種哲學觀點的數學素材.

例2比如在講Gamma函數時,得到其具有如下遞推性質：

Γ(s+1)=sΓ(s)=s(s-1)…(s-n)Γ(s-n).

如果s取正整數n+1,則上式變為

由此就會發現,Gamma函數實際上就是階乘的推廣.

例3比如在講函數的導數時,由一階公式：

二階公式：

再結合數學歸納法,得到函數f(x)的高階導數公式：

如果將自然數n推廣到一般的正實數α,就得到如下左Grunwall-Liouvill分數階導數[9]：

如果利用向前差分,也可以類似得到右Grunwall-Liouvill分數階導數定義,這就說明分數階導數就是一般的整數階導數的推廣和延伸.再進一步，可以告訴同學們分數階導數能夠對復雜環境中所涉及的歷史記憶性和空間全域相關性等反常現象提供更為深刻全面的闡釋,由它發展起來的分數階微分方程成為描述各類復雜力學與物理行為的重要工具之一,已經受到越來越多學者的關注.若以以上的例子為切入點,可以使學生接觸到當代數學的前沿理論和研究的熱點問題,從而拓寬了學生的知識面,提高了學生學習數學的能力.

3.4 巧將某些數學概念和古詩詞相聯系

文學側重于形象思維,而數學更側重于邏輯思維,前者是感性的代表,而后者是理性的代表.文學與數學之間的關系就像太極八卦圖,感性和理性之間需要達到均衡.因此,在《數學分析》的教學過程中,如果能將文學的成分融入課堂,不僅能加深學生對數學概念的記憶和理解,增強學習的趣味性和主動性,而且利于塑造健全的人格和品行.下面通過兩個例子來說明如何巧妙地將古詩詞和一些數學概念相結合.

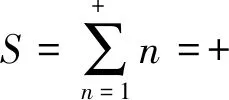
一片兩片三四片,五六七八九十片,千片萬片無數片,飛入梅花總不見.

這里用n代表雪花的數量,用求和表示雪花在飛入梅花的過程,最后的結果+∞則體現的是雪花最終消融的結局.

例5在講到整數階導數時,可以通過引導學生查閱相關資料,歸納出分數階導數常見的一些定義,如選取如下的左右Riemann-Liouville 分數階導數[9]：

而這也可以和唐代文學家、詩人,初唐詩文革新代表人物陳子昂的名作《登幽州臺歌》：“前不見古人,后不見來者.念天地之悠悠,獨愴然而涕下”相聯系.若以x代表當前的時間節點,則左Riemann-Liouville導數的積分區間(-∞,x]，可以對應“前不見古人”這句,而右Riemann-Liouville導數積分區間[x,+∞)，可以對應“后不見來者”這句.

4 結語

《數學分析》是數學與應用數學專業的核心基礎課程,數學概念抽象且技巧性強,使得學生在學習過程中很難適應.而對于肩負人類歷史繼承和文化傳承的當代大學生來說,從大學一年級的《數學分析》課程中就融入數學文化,不僅能開闊他們的視野,讓他們感悟數學的魅力,領會數學的思想,提高學習的積極性,而且可以造就他們開拓進取、求真務實的創新精神和良好品格,適應時代發展,實現自身價值.