基于R軟件的醫學統計學案例教學

陳超 潘海燕

摘? 要：R軟件具有強大的統計分析功能，將R軟件作為輔助教學手段引入醫學統計學課程的教學過程，能幫助學生加深對統計學理論知識的直觀理解，提升教學質量，增強教學效果。以t檢驗這一章節為例，通過實際教學中的案例探討進一步說明R軟件輔助教學的優勢。

關鍵詞：R軟件;醫學統計學;教學

中圖分類號：G642 文獻標志碼：A? ? ? ? ?文章編號：2096-000X（2021）02-0100-04

Abstract： R software has powerful statistical analysis functions. Using R software as an auxiliary teaching method into the teaching process of medical statistics courses can help students deepen their intuitive understanding of statistical theoretical knowledge， improve teaching quality， and enhance teaching effects. Taking the t-test as an example， the advantages of R software-assisted teaching are further explained through case studies in actual teaching.

Keywords： R software; medical statistics; teaching

醫學統計學是多數醫學專業的基礎必修課程之一，該課程涉及方法學理論知識較多，計算量大，是學生覺得難度較大的幾門課程之一。如何通過教學改革增強教學效果，提高教學效率，促使學生更好掌握統計學理論知識，是醫學院校統計學教師時常思考的一個問題。該課程要求理論實踐相結合，需要利用計算機輔助手段開展教學，在此前教學中，實習課常用SPSS軟件對數據進行分析。然而在課堂教學中，一些特殊要求SPSS軟件并不能給出滿意的呈現。本研究以提高教學效果和學生的學習效率為根本出發點，在教學過程中引入R軟件輔助教學，結合教學實際，運用任務驅動的方法，讓學生更好地理解掌握統計學理論知識。

目前已有很多成功將R軟件運用到教學過程當中的案例，沈新娣[1]和安麗霞等[2]分別在大學數學和概率論與數理統計課程引入R軟件輔助教學;劉君娥[3]在統計學課程進行實踐。將R軟件運用到醫學統計學教學實踐當中是一個合適且值得推薦的方法。本研究將以t檢驗這一章節作為例子進行詳細說明。

一、R軟件簡介

R軟件是一項主要由奧克蘭大學的Robert Gentleman和Ross Ihaka開發的統計計算系統，它提供了一個開源的統計編程環境，并且有一套完整的數據處理、計算和制圖軟件系統[4]。R軟件最大優點是用戶能夠使用全球所有優秀的統計軟件包，并且提供數據處理環境。基于R軟件的開放軟件包，在教學環節可以直接調用函數實現計算功能，十分方便。另外，教師若有新思路講解知識點，R軟件可以通過修改程序語句展示教學過程中需要的過程或結果，滿足教學過程的需要，有助于學生直觀理解。

二、醫學統計學課程的教學現狀

醫學統計學課程是高等醫學院校大多數專業的重要基礎課程之一，對學生解決實際問題能力的培養和后續課程的學習起著重要的作用。目前，醫科院校醫學統計學課程教學過程中，重實踐輕理論的趨勢愈發明顯，這跟專業特點有關。大多數醫學專業的學生沒有學習過概率論與數理統計課程，統計基礎理論知識缺乏，導致學生對醫學統計學課程的一些理論知識理解困難，進而對課程失去興趣。如何幫助學生更好理解理論知識是教師在教學過程當中需要解決的一個問題。

陸守曾[5]指出目前醫學統計學整個學科的一個特點是：基礎理論與實際應用密切相關，但前者多處于弱勢。重視實踐而忽視理論會導致學生知其然而不知其所以然。比如很多學生學完該課程知道當P<0.05拒絕原假設，卻不明白為何P<0.05等價于樣本落入拒絕域。在課堂教學中加強學生對理論知識的理解尤為重要。

三、R軟件在t檢驗章節的具體應用

（一）隨機模擬說明Z檢驗不適用于總體方差未知且樣本量較小的情況

例1.當總體方差未知且樣本量較小時，令樣本方差代替總體方差，若采用Z檢驗，即Z=■-？滋0/S■，當|Z|>1.96或P<0.05，在α=0.05水平下拒絕原假設。采用Monte Carlo隨機模擬，運用R軟件計算I型錯誤。程序如下：

n<-5? ? ? ? ? ? ? ? ? ?#樣本量為5

miu<-1;delta<-1? ? ? ? ? #均值為1，標準差為1

n1<-0

for（i in 1：100000）? ? ? ? #重復運行{}內語句100000次

{

x<-rnorm（n，miu，delta）? #隨機產生5個x

mx<-mean（x）? ? ? ? ?#計算樣本均值

d<-var（x）? ? ? ? ? ? #計算樣本方差

p<-1-2*abs（pnorm（（mx-miu）/（d/n）^0.5）-0.5） #計算P值

if（p<0.05）n1<-n1+1? ? #若拒絕原假設，結論出錯次數+1

}

zerror<-n1/100000? ? ? ?#計算I型錯誤

zerror? ? ? ? ? ? ? ? ?#輸出I型錯誤

運行該程序，輸出結果為0.12，說明α=0.05，n=5，總體方差未知時，采用Z檢驗的I型錯誤率是0.12，所以在該條件下，Z檢驗不適用，需要考慮新的統計分析方法。

（二）比較總體方差已知與未知的區別

態分布更“扁”的分布，稱為t分布。R程序如下：

set.seed（11）

n<-5? ? ? ? ? ? ? ? ?#每次抽樣為5

time<-30? ? ? ? ? ? ?#重復抽樣30次

x<-matrix（rep（0，n*time），time，n）

mx<-vector（）; s<-vector（）

for（i in 1：time）

{

x[i，]<-rnorm（n，2，4）? ? ? #均值為2，標準差為4的總體中抽取5個樣本

mx[i]<-mean（x[i，]）? ? ? #計算5個樣本的均值

s[i]<-sd（x[i，]）? ? ? ? ?#計算5個樣本的標準差

}

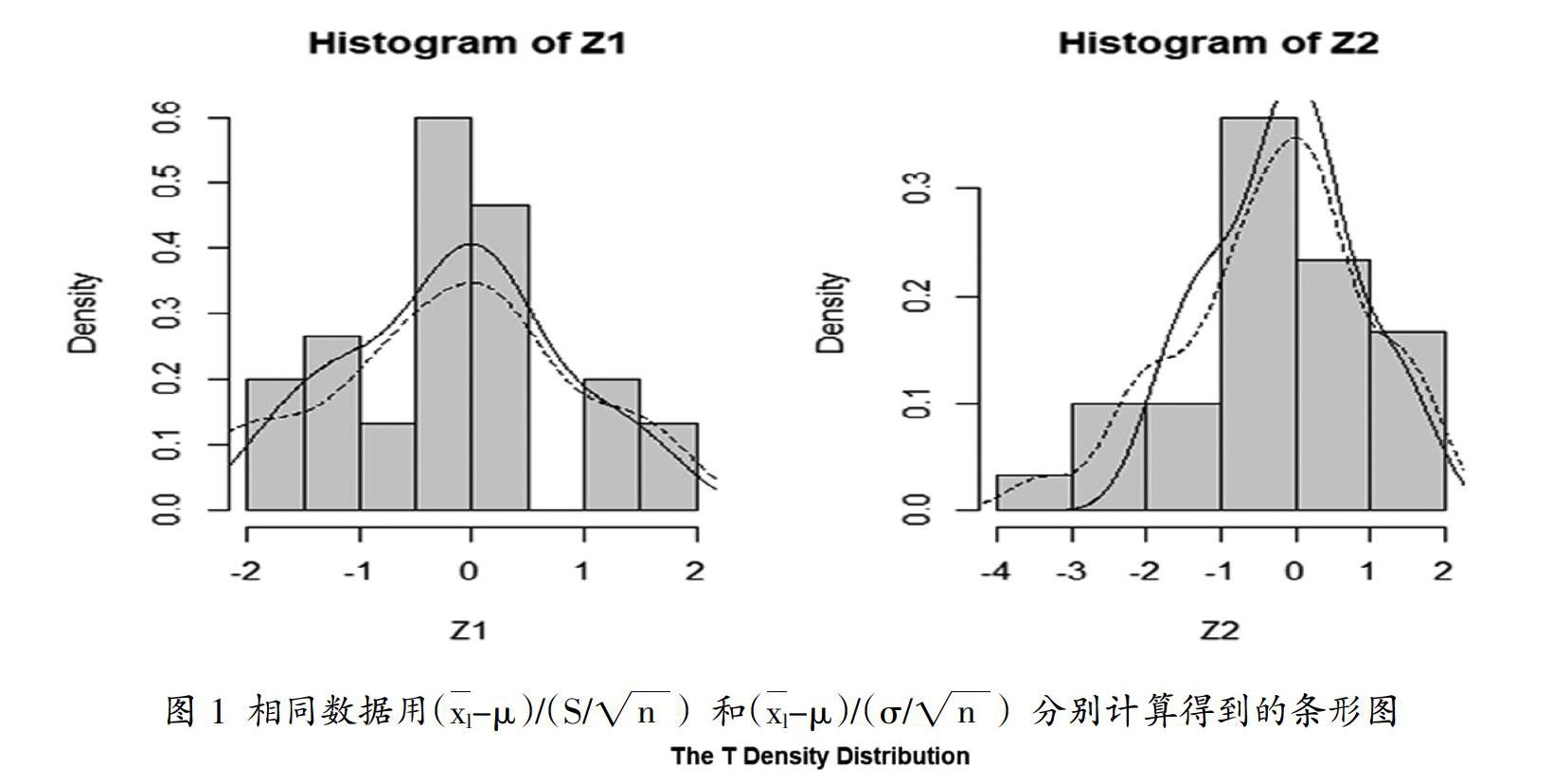
Z1<-（mx-2）/（4/n^0.5）? ?#總體方差已知，計算（xl-？滋）/（？滓/■）

Z2<-（mx-2）/（s/n^0.5）? ?#樣本方差代替總體方差，計算（xl-？滋）/（S/■）

par（mfrow=c（1，2））

hist（Z1， freq=F）? ?#Z1直方圖

lines（density（Z1）， col="red"）? ?#實線畫Z1的密度函數曲線

lines（density（Z2）， col="blue"）? ?#虛線畫Z2的密度函數曲線

hist（Z2， freq=F）? ?#Z2直方圖

lines（density（Z1）， col="red"）? ?#實線畫Z1的密度函數曲線

lines（density（Z2）， col="blue"）? ?#虛線畫Z2的密度函數曲線

圖1左右圖分別為根據樣本計算得到

（三）R軟件協助探索t分布的特點

例3. 講解t分布的特點。在R軟件中，輸入以下程序，通過修改自由度df的取值，可觀察不同自由度的t分布密度曲線，讓學生探索t分布密度函數曲線與自由度的關系以及t分布與標準正態分布的關系。

df1<-2 #設置自由度為2

df2<-5 #設置自由度為5

x<-seq（-5，5，length.out=1000）;? ?y<-dt（x，1，0）

plot（x，y，lty=1，xlim=c（-5，5），ylim=c（0，0.45），type='l'，xaxs="i"，yaxs="i"， ylab='density'，xlab=''，main="The T Density Distribution"） #實線畫自由度為1的t分布密度函數

lines（x，dt（x，df1，0），lty=2） #自由度為2的t分布密度函數

lines（x，dt（x，df2，0），lty=3） #自由度為5的t分布密度函數

lines（x，dnorm（x），lty=4） #標準正態分布密度函數

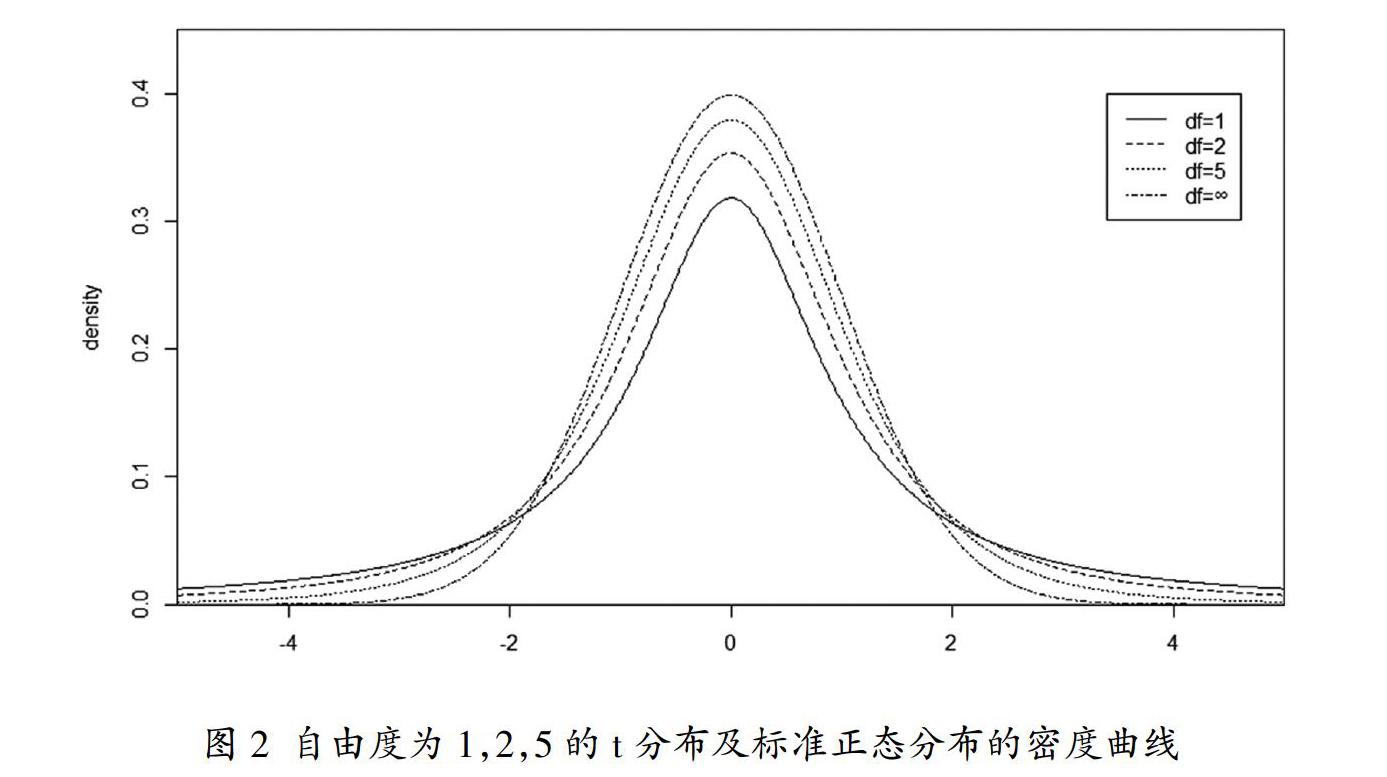
legend（3.4，0.4，c（"df=1"，"df=2"，"df=5"，"df=∞"）， lty=1：4）

圖2讓學生直觀了解到t分布的密度函數曲線關于x=0對稱，形狀和自由度有關，在接近0處比標準正態分布小，遠離0處比標準正態分布大，且自由度越大越接近標準正態分布。課堂教學中可以通過修改df1和df2的取值向學生呈現不同自由度的t分布密度函數曲線。當自由度大于50時，t分布密度函數曲線和標準正態分布函數曲線差距很小。

（四）R軟件比較Z檢驗和t檢驗原假設，當|A|>2.776，t檢驗拒絕原假設。Z檢驗拒絕原假設的可能性較大，犯I型錯誤率較大。兩者比較程序如下：

n<-5? ? ? ? ? ?#樣本量，分別輸入5，50，500

miu<-1;delta<-1? ? ? ? ?#均值為1，標準差為1

z1<-0;t1<-0

for（i in 1：100000）

{

x<-rnorm（n，miu，delta）? ? ?#隨機產生5個值

mx<-mean（x）? ? ? ? ? ? #求x得均值

s<-var（x）? ? ? ? ? ? ? ? #求x得方差

A<-（mx-1）/（s/n）^0.5? ? ? ?#計算統計量

t<-qt（0.975，n-1）? ? ? ? ? #計算t界值

z<-qnorm（0.975）? ? ? ? ?#計算Z界值

if（abs（A）>=t）t1<-t1+1? ? ?#判斷是否拒絕原假設

if（abs（A）>=z）z1<-z1+1? ? #拒絕則犯錯次數+1

}

terror<-t1/100000? ? ? ? ? #t檢驗錯誤率

zerror<-z1/100000? ? ? ? ?#Z檢驗錯誤率

terror; zerror

n=5，50，500時，輸出結果分別為（0.05，0.12），（0.05，0.055），（0.05，0.05），即t檢驗I型錯誤率為0.05，Z檢驗的錯誤率隨著樣本量的增加逐漸接近0.05。說明t檢驗的結果比Z檢驗結果更加精確，大樣本情況下可以用Z檢驗。

（五）R軟件協助計算t檢驗的P值

例5：計算出t值之后，根據自由度df和顯著性水平α，計算t界值：雙側檢驗用語句qt（1-α/2，df），單側上界用qt（1-α，df），下界用qt（α，df），其中α為顯著性水平，df為t分布的自由度。程序如下：

alpha<-0.05? ? ? # α=0.05

n<-10? ? ? ? ? ?#樣本數為10

df<-n-1? ? ? ? ? #自由度

qt（1-alpha/2，df）? ?#雙側t界值

qt（1-alpha，df）? ? ?#單側t界值

將t值與t界值進行比較可得出結果，或直接求P值，程序如下：

n<-10? ? ? ? ? ? #樣本數

t<-1.833? ? ? ? ? #計算得到的t值

p<-pt（t，n-1）

twop<-1-2*abs（p-0.5）

onep<-2*twop

twop? ? ? ? ? ? ?#雙側P值

onep? ? ? ? ? ? ?#單側P值

四、結束語

醫學專業的學生概率統計的知識基礎不扎實，剛接觸t檢驗這一章節，對知識點的理解比較吃力，尤其是分位點函數、累計分布函數這些專業概念，導致對理論知識難以理解。本研究針對該特點，通過在課堂中引入R軟件協助教學，從問題出發，借助R軟件讓學生直觀理解抽象的理論知識，引導學生思考探索，提高教學質量。

引入R軟件輔助教學，既能運行程序語句輔助案例講解，加深學生對知識點的理解，又能簡單快速計算結果，提高學生運用統計知識解決實際問題的能力，并且能將理論知識和實際操作聯系起來，大大提高學習效果，幫助學生更好地學習t檢驗。

參考文獻：

[1]沈新娣.基于R軟件的數學實驗在大學數學教學中的應用初探[J].衛生職業教育，2018，36（06）：77-79.

[2]安麗霞，盧丑麗，燕揚.初探R軟件在獨立院校概率論與數理統計教學中的應用[J].大學教育，2018（09）：102-104.

[3]劉君娥.R軟件在統計學教學中的應用——以因子分析模

型為例[J].廣西科技師范學院學報，2019，34（03）：149-152.

[4]薛毅.統計建模與R軟件[M].北京：清華大學出版社，2007.

[5]陸守曾.對醫學統計學應用現狀的四點看法[J].中國衛生統計，2010，27（02）：114-115.