數學結構化教學的學材開發與學程設計
——以“分數的意義”的教學為例

孫 謙

開展數學結構化教學，教師應致力于尋找知識之間的連接點，將碎片化的知識連成線、織成網、筑成塊、構成體，讓學生整體感悟學習內容、學習進程，建構自己整體的思維體系和認知結構。這種動態建構的過程，是教師基于對課程與課標的理解以及對學理的分析和學情的調研，著力將教材改編為學材，即教師根據自己對知識結構與學生認知結構的專業化理解，設計連接學生認知經驗的“真實”情境，引導學生發現數學問題，找到相關聯的數學元素，從而建構起自己的認識結構。

一、組織基于真實情境的學習過程，聚焦數學本質

《義務教育數學課程標準（2011年版）》明確指出：為了幫助學生真正理解數學知識，教師應注重數學知識與學生生活經驗的聯系、與學生學科知識的聯系，組織學生開展實驗、操作、嘗試等活動，引導學生進行觀察、分析，抽象概括。教師應努力挖掘隱藏于生活中的學習素材，并引導學生通過現實生活素材理解數學，同時將所學的數學內容應用于現實生活。數學結構化教學特別強調從“真實”情境中來，到“真實”問題中去，基于對學生學習和生活經驗的了解和分析，整合教材資源，創新設計教學活動和學習過程。

例如：教學蘇教版下“分數的意義”時，首先，教師以學生真實的生活情境——測量黑板的長度引入，將生活與數學有機聯系起來，延展開去，聚焦測量的本質——數與量的產生，開啟了學生對數的發展過程的整體認識；其次，轉向生活中常見的分數形態——面積的均分，從顯而易見的可視化表征中抽象出用分數表達平均分的實質；再次，引導學生經歷測量的過程，感受分數作為一種“數”，與學過的整數、小數一樣，不僅可以表示量的多少、數的大小，還可以表示一些計數單位不斷累加的結果；最后，從另一種角度看待面積均分產生的分數，深入挖掘分數表示“率”的又一深刻內涵。整個過程前后呼應，于“變”中求“不變”，轉換連續而自然，抓住分數不同方面的意義，既有聯系又有區別，讓學生真實而深刻地感受到分數產生的必要性和必然性。

二、開發動靜結合的學習材料，突破學習難點

“分數的意義”建構過程中重要的一點，是引導學生認識到分數作為一種“數”的實質。也就是說，它與其他數一樣，都能在數射線上找到自己的位置。張奠宙先生曾多次強調在數射線上對分數作幾何解釋的重要性。然而，數射線的抽象程度較高，學生不易掌握，如何設計易于學生操作和理解的學材，幫助學生突破這一學習難點呢？不少研究都表明，從細長的條形塊這一幾何模型出發，逐漸抽象出數射線，更加符合學生的認知發展特點。

基于此，教師設計了一根一米長的軟尺，利用這個學材，組織學生開展了一系列“做中學”的活動，如量一量、圈一圈、比一比等。首先，引導學生用軟米尺測量黑板的長度，從中感悟到分數產生的必然性。然后，用軟米尺圈出一個圓，動線成面，化直為曲，將面積均分與計量單位均分聯系起來。無論是長條軟米尺的均分還是圓的均分，都可以看成是對現實存在的“物”的均分，這是分數的重要意義之一。軟米尺和圓中扇形的色塊一一對應，可以讓學生感受到分數的不同表征形式之間的轉換和聯系。最后，教師帶領學生利用軟米尺測量窗戶的長度，化曲為直，讓學生親眼見證比1小的數和比1大的數都可以用分數表示，整數與分數可以進行轉化。軟米尺自然與數射線融通，變成了一個可以無限延展的數射線。在引導學生認識分數的多層含義的過程中，可靜可動的學材發揮了巨大的作用。

三、呈現元素聯結的變式材料，開闊數學視野

數學概念的結構化教學主要通過元素的聯結來實現。這就要求教師深刻把握概念的本質內涵和豐富外延，不斷分解和重組學習材料，變化表征形式，讓原本孤立無關的材料變成聯系緊密的變式材料，達到”橫看成嶺側成峰“的效果，最終促進學生自主建構概念?！胺謹档囊饬x”之所以成為學生學習的一個難點，其中一個重要的原因，就是雖然分數問題通過分割操作可能轉化為整數問題，但與整數不同，分數是一個表示兩個量倍比關系的相對量，或者說是一個比例，這種認知沖突有時會對學生的學習產生負遷移。對學生來說，分割計數產生分數是易于理解的，分數表示兩個量之間的倍比關系是較難理解的。在教學中，教師要注意從學生已有的利于他們理解的經驗出發，靈活變換，螺旋上升，提高學生對概念的整體認知。教師可以將學生熟悉的正方形和人民幣作為研究對象，不斷變換表征形式（如下頁圖1），拓展學生的思維，激發其對于分數表示倍比關系的思考，深化其對概念的認識。

師：現在變成了這樣（1 元、2 元、5 元、10 元人民幣各一張），你還能看出分數嗎？

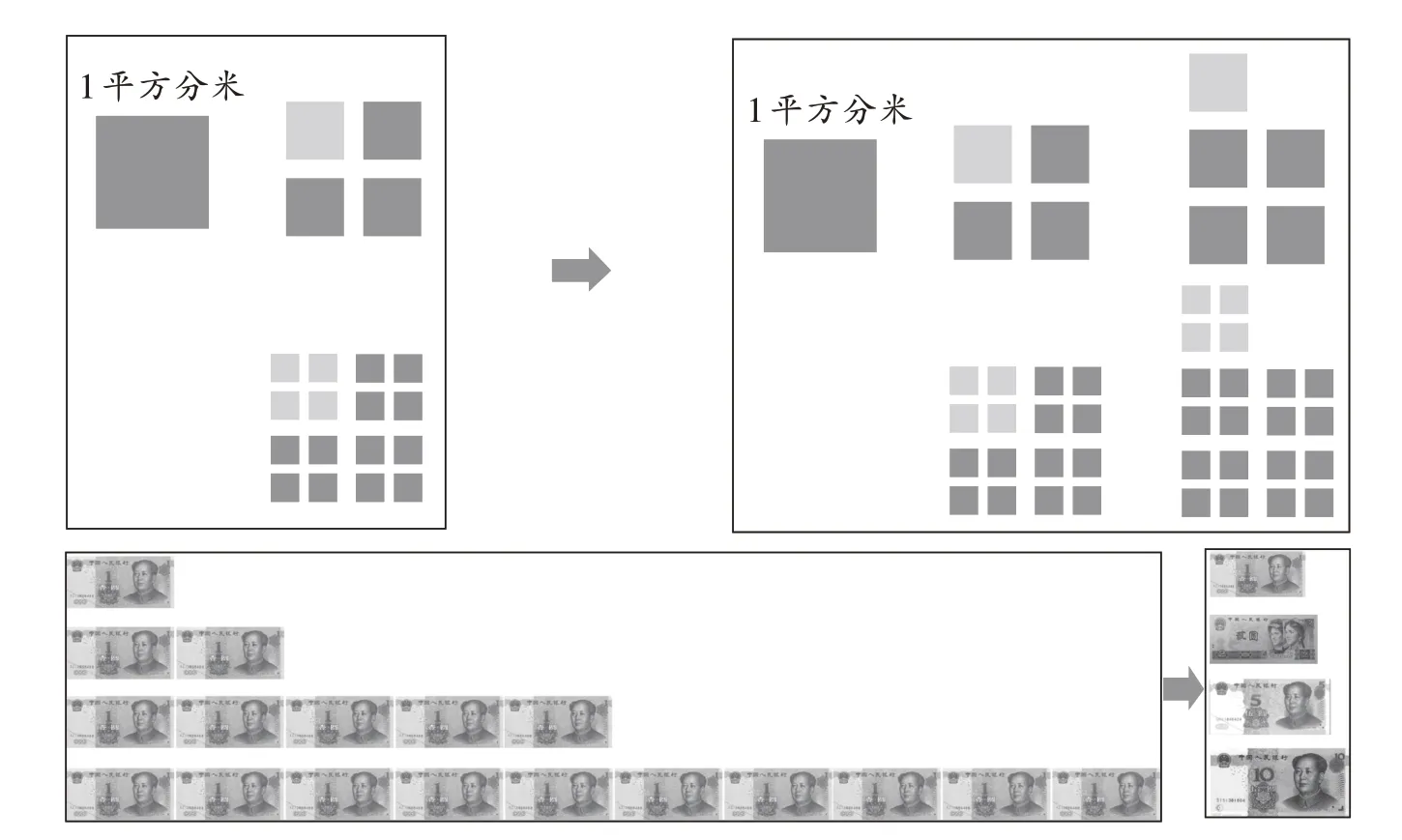
圖1 以正方形和人民幣為例探究“分數的意義”

一些學生臉上露出了困惑的表情。

以上以“分數的意義”的教學為例，分析了結構化教學中學材開發和學程設計的實施要點——在“真實”情境中，注重運用多元表征，創新應用模型，引導學生開展合作探究，實現實際意義的關聯建構，發展抽象、推理、模型等綜合能力，完善認知結構，在想象、修正、反思中提高認知水平，在對話、操作、合作中促進心智發展。