數學結構化教學的學評調節
——以“分數的意義”的教學為例

周 萍

《義務教育數學課程標準（2011 年版）》指出：學習評價的主要目的是全面了解學生數學學習的過程和結果，激勵學生學習和改進教師教學。在數學結構化教學中，學評調節的作用，就是反饋學生結構化學習的效果，為學生持續、深入地開展結構化學習提供清晰的線路圖和風向標。我們倡導采用表現性評價，考查學生能否在真實或模擬的生活情境和數學情境中，運用先前獲得的數學知識經驗，用整體關聯的思想去解決新的問題。本文以蘇教版五下“分數的意義”一課的教學為例，通過對比測評的方式，展現學生結構化學習目標的達成情況及其認知結構的發展變化情況，反饋教學過程中可供調節的學習節點，為教師更好地開展結構化教學提供依據。

一、測評題的設計及發放

在數學結構化教學中，教師設計測評問題要基于整體關聯的思想，緊扣知識核心，呈現出綜合性強、開放度高的特點，還要便于學生思考探索與理解表達。基于此，本課的測評題設計如圖1所示。

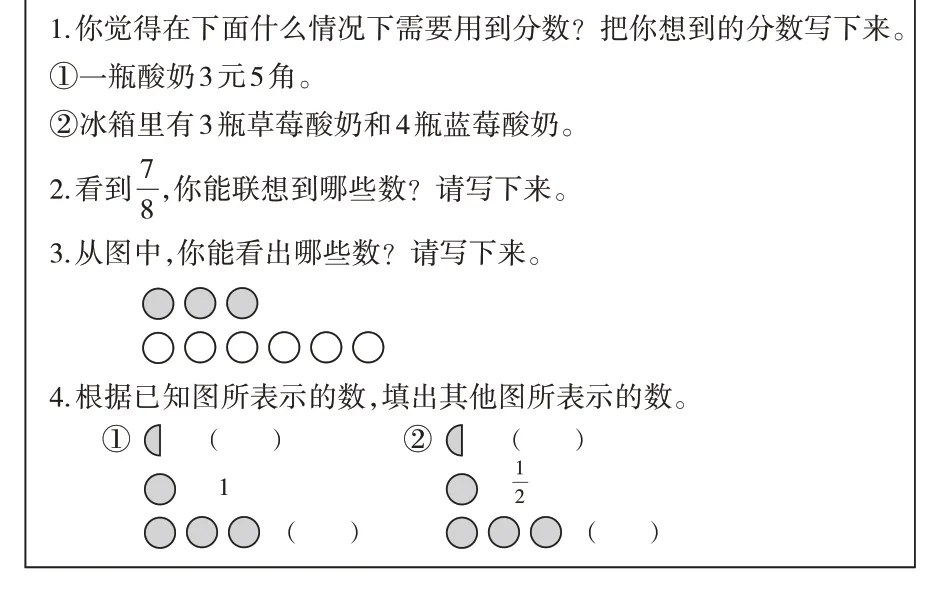
圖1 “分數的意義”測評題

為了不占用學生較多時間，又能得到每道題的反饋數據，全班48 位學生被分為4 組，1 組完成1題，每位學生在課前及課后5分鐘內各測試一次。本次對比測試每題樣本數課前、課后均為12份。

二、測評結果及發現

在對比測評完成后，教師對學生的完成情況進行數據統計及分析，發現如下：

其一，學生使用分數表達數量及數量關系的人數占比提升明顯。第1 題的兩個情境并非一定要用分數來表達，課前用分數表達的學生占40%，課后達到91.7%。

其三，面對以不同表征形式呈現的問題，學生理解表達起來差異較大。相較于以文字表征的第1 題，學生從不同角度理解以圖形表征的第3 題的人數更多。第2 題以算術模型呈現數量關系，從學生的回答可以看出，他們思考的視角不夠開闊，與第3題相比，反差比較大。

三、測評給我們的啟示

（一）追根溯源：學習層階的推進路徑

1.連續經驗，驅動學習發生。

學生在“量而有余”的情境中調動原有的知識經驗，對分數進行解釋并建立分數單位與長度單位的對應關系，既是分數意義學習的基礎，也便于學生在之后的學習中將分數看成分數單位累加的結果，實現經驗、認知與方法的連續溝通，讓學習真正發生。

2.關聯意義，發展認知結構。

在尋找、回顧、創造、概括分數的過程中，學生體會到語言表征的抽象概括性及核心概念間的勾連。在軟米尺上找分數、數分數，觀察由尺延伸形成的數射線模型，學生得以跳出“部分—整體”關系，從分數單位累加的角度理解分數，為假分數的建立做好解釋，并在分數與整數之間建立起聯結。在這一環節，學生的認知結構初步形成。

3.循環活動，實現內化遷移。

學生在活動中進一步理解分數的意義，在表達“部分—整體”關系時從數量比走向份數比，再從“部分—整體”關系走向同類量間的關系，并在自主定義單位“1”及以分數單位表示分數的過程中，鋪墊了分數與除法的關系，學生從不同角度，對“一個量占另一個量多大份額”的分數本質有了深入理解，有助于知識的內化遷移。在這一環節，學生實現了對分數意義的整體認識，認知結構得以完善。

（二）精益求精：學評調節的節點展現

1.合理匹配學材與目標，讓學習更符合學生的認知邏輯。

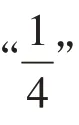
（圖2）

2.關注表征及重新表征，促進學生整體性認知結構的建立。

測評反映出學生對圖形表征的內容理解得更全面，對文字表征不夠敏感。這主要是因為圖形表征更直觀，有利于學生把握對象的全貌和本質。教師在呈現文字表征時，不妨借助數形結合，引導學生充分理解、多元表達，幫助他們更好地建立整體性認知結構。

3.聚焦核心概念理解，讓學生對模糊認知正確歸因。

測評中一些學生對分數的認知有些模糊，錯誤呈現出一定的延續性——有較大可能會在學習假分數、分數乘法等內容時繼續出現。在后續的教學中，教師要注意引導學生充分調用本課所學，讓“分數的意義”這一核心概念的正確理解成為后續知識的生長點。

在上述實踐中，筆者體會到課堂觀察的點面結合及測評題的科學設計是客觀、科學評價的保證。總之，筆者對小學數學結構化教學的學評調節的研究還處于初級階段，還有待進一步研究與探索。