HPM視角下的初中數學單元整體復習教學

余立海　栗小妮

【摘 要】研究者利用14世紀意大利的一個關于土地分配的法律案例設計圓的基本性質復習教學，引導學生利用角平分線的性質、三角形的兩邊之和大于第三邊、同一直角三角形中斜邊大于直角邊等知識對原法律案例進行解釋，通過對原法律案例進行問題變式，讓學生綜合運用與圓的基本性質有關的知識解決問題，提升了數學建模的意識與能力，并整體性復習初中階段與圓相關的知識。

【關鍵詞】圓的基本性質;數學史;數學建模

【作者簡介】余立海，杭州市蕭山區南陽初級中學數學教師;栗小妮，教育學博士，上海市長寧區教育學院教研員。

【基金項目】上海高校“立德樹人”人文社會科學重點研究基地之數學教育教學研究基地研究項目——數學課程與教學中落實立德樹人根本任務的研究（A8）

在全國積極深化義務教育課程改革，落實立德樹人根本任務之際，研究適合改革需要的課堂教學刻不容緩。然而，筆者經調查發現，當前已有的復習課教學大部分以“練習+講評”為主[1]，課堂教學乏味且低效。很多教師對課程標準、教材以及試題缺乏研究，直接將教輔資料的內容作為上課的主要內容。還有的教師因為復習課時間緊，往往采用一講到底或邊做邊講的模式，學生沒有思考和表達的機會。復習課的教學目的之一是將碎片化的知識體系化，而有的教師因為找不到合適的線索把要復習的知識串聯起來，所以只能讓學生重復操練，學生往往不清楚自己解決了什么問題。究其原因，主要是教師未能提供相對真實并可供解決的問題背景。

整體教學以知識的相互關聯性、整體性與學習者的參與性為原則[2]，倡導情境式的、問題定向的、案例式的、社會性的和內在驅動的教學方式，利用講練結合、支架式生成與建模等策略使學生獲得有意義的學習[3]。而復習課就是要幫助學生建構知識之間的聯系，形成對知識的整體理解，在建立知識之間的聯系的過程中，領悟數學的思想方法，在應用知識解決問題的過程中，積累數學活動經驗[4]。所以，筆者嘗試利用中世紀一個典型的法律案例進行單元整體復習教學設計，讓學生參與到有意義的情境任務中，通過問題解決，建構和完善相關知識體系。

一、歷史素材

1355年，意大利法律教授巴托魯斯（Bartolus）討論過一個關于淤積地分割的案例：如圖1，具有公共邊界OC的甲、乙兩塊土地的主人都想獲得洪水過后所產生的一塊肥沃的淤積地OAB（其中甲、乙兩塊土地與淤積地接壤的邊界為不規則曲線AOB，河岸線AB也為不規則曲線），雙方該如何分割淤積地呢？

有人建議延長已有的分割線CO將淤積地進行分割，但這樣的分割方式可能會引發爭端。巴托魯斯教授意識到要公正合理地解決這樣的問題非常重要。他發現早在公元160年的羅馬法律著作中就有類似的問題出現，法律著作中雖然沒有給出實際的解決方案，但給出了一個一般性的分割原則。淤積地是由于河水沖刷原有的土地而形成的，那么分割的原則就是“沖刷誰的地形成的歸誰”。基于這樣的原則，巴托魯斯教授給出了淤積地分割的方案：淤積地中的任何區域，離誰家原有土地更近，就歸屬誰家。

巴托魯斯教授將這一原則應用于不同的幾何情境中。如若邊界線AOB是一條線段，那么，分割線就是過點O作垂直于AB的線段;若邊界線AOB構成一個角（如圖2），那么，分割線就是∠AOB的角平分線;若邊界線AOB構成圓弧，則分割線是圓心與點O的連線。

荷蘭學者馮馬楠（Jvan Maanen）認為，將類似這樣的生活中的真實問題融入課堂，可以實現數學和其他學科的融合，如本案例可以實現數學和法律的融合，讓學生用數學的方法解決法律問題，體會數學的應用價值。這樣的分割原則，在一些國家的法律中現在也依然在用[5]。

“圓的基本性質”是浙教版數學九年級上冊第3章的教學內容。學習圓的基本性質對于學生邏輯推理能力的培養，數學思想方法的形成都有著重要的價值。基于以上原因，筆者利用上述法律案例設計問題串，對圓的基本性質復習課進行教學設計，并擬訂以下教學目標。

（1）能對本法律問題發表自己的觀點，知道問題的歷史解決方案，并知道法律問題的解決需要滿足公平、公正和可操作的原則。

（2）能通過建立數學模型，根據圓的基本性質和相關知識解決該問題的延伸問題串，培養學生分析問題和解決問題的能力。

（3）在問題解決過程中，體會數學的應用價值。

二、教學設計與實施

（一）情境引入

教師將原法律案例進行了改編（將分割線OA、OB分別改成了線段[6]），如圖2，并在上課前一天發放學習單，讓學生自行設計分割方案。

課上，教師投影部分學生的分配方案，然后讓對應的學生說明自己設計的分配方案的依據，教師在學生表達自己的觀點后與其他學生一起進行評價。

師：根據收集上來的統計情況，同學們的分配方案主要有平均分配、補差分配、按比例分配、按分割線分配等，其中大部分同學都是按分割線分配，可見大家都喜歡從數學的角度來思考問題。老師選了一些比較典型的分割線分配方案，請同學們自己來說一說這樣分配的依據。

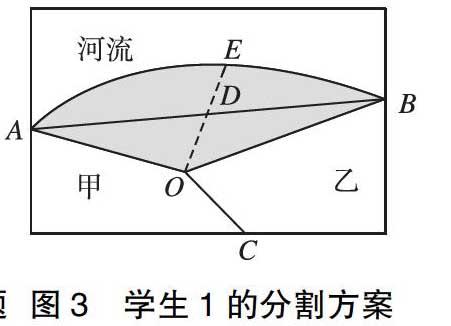
生1：我想盡量平均分配，方法是連接AB，取AB中點D，連接OD并延長至河岸線交于點E，OE為分割線（如圖3）。

師：這位同學表述非常規范，用了“盡量”平均，因為他這樣操作并不一定能平均。

生2：我也是想盡量平分面積，方法是取河岸線AB的中點C，連接OC即為分割線。

師：這位同學也用了“盡量”平分，因為他這樣操作也并不一定能平分，而且不規則曲線AB的中點很難找到。

生3：我是想盡量按比例分，方法是過點O作一條分割線使得Sa∶Sb=S甲∶S乙。

師：由于不規則，這位同學的分割線也很難準確得到。

生4：我是想盡量平分面積，方法是連接AB，作AB的中垂線，中垂線與河岸和邊界的交點連線作為分割線（如圖4）。

師：這位同學也想平分這塊淤積地的面積，但這樣的操作也無法真正平均分配。

師：聽了同學們的講解，我發現大多數同學都希望平均分配，都希望公平、公正地解決這個問題，但具體的操作和同學們所想的依據并不完全符合，而按比例分配可能會造成多的越多，少的越少的情況，也無法得到甲、乙雙方的認可，而且操作起來也非常困難，那么當初這個問題又是如何解決的呢？我們一起來看一下。

教師先出示巴托魯斯教授的分配依據——就近，并說明此依據當初得到了甲、乙雙方的一致認可，然后介紹在這樣的依據下的具體操作，并提出新的問題。

師：巴托魯斯教授這樣操作為什么符合離誰原有土地邊界近就歸誰這個依據呢？

生：他利用角平分線的性質，角平分線上的點到角兩邊的距離相等。

師：那為什么角平分線右邊的點離乙的邊界OB更近呢？

生：假設任意取點P，先向兩個邊界作垂線段，記作PM、PN，量取后進行比較即可。

師：你說的方法能解決點P，但其余的點呢？我們都靠量取的話這個工作能做得完嗎？

生：如圖5，我們可以記PM與角平分線的交點為C，過點C再作OB的垂線，與OB交于點M′，由角平分線的性質可得CM=CM′，所以根據三角形兩邊之和大于第三邊，以及在同一三角形中，斜邊大于直角邊可以得到PM=PC+CM=PC+CM′>PM′>PN。

師：同學們借助數學知識科學地解釋了點P離分界線OB比較近，由于點P的任意性我們可以說明角平分線右側的點都離分界線OB比較近，反之也可以用同樣的方法去說明左側的點離分界線OA比較近，這樣就能解釋他的操作是符合當時的分配依據的。

（二）情境再創

因為本節課的目標是復習圓的基本性質，而且學生之前的分割方案中已涉及圓的相關性質，所以教師采用對學生分割方案通過情境再創的方式進行問題設計，這樣既可以縮短理解新問題的時間，又可以提高學生的學習興趣。

問題1：如圖6，在學生做法的基礎上，連接AB，分別作AB與OB的垂直平分線，并交于點D，若此時淤積地的法定分割線恰為OD的一部分，判斷原邊界線OA和OB的數量關系。

生1：如圖6，過點D作AO的垂線交AO于點M，因為DN⊥BO，且DO是角平分線，則由角平分線的性質定理可得到DM=DN，作圖可知點D是△ABO的外接圓圓心，所以根據圓心角定理的逆定理可以直接得出AO=BO。

生2：由DO是角平分線，則∠AOD=∠BOD，又因為點D是△ABO的外接圓圓心，所以根據圓周角定理的推論——同圓或等圓中，相等的圓周角所對的弧相等，可以得到與弧AO和弧BO度數互補的弧相等，則AO=BO，再根據圓心角定理逆定理可以得到AO=BO。

生3：還可以先證明△DOM≌△DON，得到MO=NO，然后由垂徑定理得到AO=2MO，又由條件知BO=2NO，得到AO=BO。

師：很好，同學們用到了圓周角定理的推論、圓心角定理逆定理、垂徑定理以及三角形全等等數學知識證明AO=BO。

（三）問題遷移

在不改變分割規則的前提下，教師通過改編原始圖形設計問題，讓學生在解決問題的過程中，進一步復習圓的相關性質。

問題2：如圖7，邊界線AOB為長度80米的線段，且河岸線為一段半徑為50米的圓弧，則淤積地的法定分割線如何畫？[6]

圖7

生：只要過點O作AB的垂線交弧AB于點H，OH即為所求分割線，其實還是角平分線，只是現在是一個平角而已。

師：非常好，這位同學不僅給出了分割線，還解釋了原因。那這個法定分割線OH的長度可求嗎？

生1：會隨著O點位置的改變而改變，只有點O確定才可求。

師：那我們選一個特殊的位置，比如中點，然后試著計算它的長度。

生2：如圖8，延長HO，由HO是弦AB的中垂線，根據找圓心的方法可知圓弧AB所在圓的圓心一定在射線HO上，假設為點D，連接BD，由勾股定理可得DO=30米，則HO=20米。

師：那如果不是中點，而是AO∶BO=1∶3，還可以求嗎？

生3：如圖9，在原來的基礎上假設有一點O′滿足AO′∶BO′=1∶3，再構造一個由半徑、半弦、弦心距組成的Rt△DMH′，和剛才一樣利用勾股定理就可以求解。

師：非常好，從方法上來看，在知道半徑和弦長的情況下，只要知道AO∶BO的值，就可以求出此時分割線OH的長度，請同學們課后思考AO∶BO=1∶n時的情況。

（四）變式深化

在不改變分割規則的前提下，教師在問題2的基礎上，進一步改編原始圖形，將邊界線改為圓弧，讓學生尋找解決問題的方案。

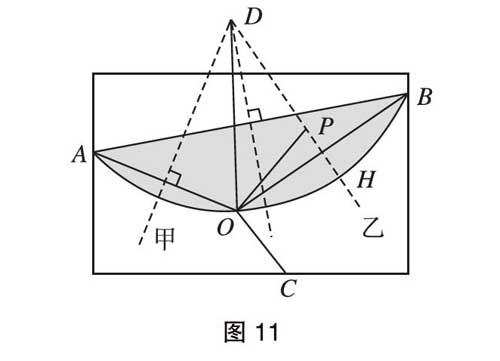
問題3：如圖10，若邊界線AOB為圓弧，該如何分配淤積地？[6]

師：如果我們繼續改變邊界線和河岸線的形狀，若邊界線AOB為圓弧，則按照剛才的分配依據，你能不能把分割線畫出來？

生1：如圖11，在淤積地區域任意找個點P，那么從圖中點P的位置可以猜想點P與邊界AO的最近的點就是點O，即PO的長，而點P與邊界BO最近的點是過圓心D時直線DP與邊界BO的交點H，即PH的長，目測PH

師：誰能借助已學的數學知識用推理的方式解釋PH

生2：根據三角形中任意兩邊之和大于第三邊得PD+PO>OD=DH=PD+PH，即PH

師：也就是說，淤積地中任意一個點與圓心D連接的直線與邊界線的交點在哪家邊界上就離哪家的邊界近，這樣就能解釋為什么分割線是DO上的一段。

（五）回顧總結

在該教學環節，教師引導學生從以下幾個方面進行總結。

（1）一個原則。淤積地分割問題的解決原則是對雙方都公平、公正，即雙方都認可的分配方案且具有可操作性。從最初的淤積地分割到教師改編的問題2、問題3都遵循了一個基本準則——就近。

（2）一塊知識。本節課利用淤積地分割問題整體復習了與圓的性質有關的知識。在分配方案的解決過程中，主要運用以下數學知識：①角平分線上的點到角兩邊的距離相等;②三角形的兩邊之和大于第三邊;③直角三角形的斜邊大于直角邊。在問題1的解決過程中，主要復習的數學知識有：①不在同一直線上的三點確定一個圓;②圓心角逆定理——在同圓或等圓中，相等的弦心距所對的弦相等;③圓周角定理的推論——同圓或等圓中，相等的圓周角所對的弧相等;④圓心角逆定理——在同圓或等圓中，相等的弧所對的弦相等;⑤全等三角形的判定方法（AAS）;⑥垂徑定理——垂直于弦的直徑平分弦，并且平分弦所對的兩條弧。

問題2和問題3都對原情境進行了改編，增加了學生的思維難度，考查學生綜合利用知識的能力。問題2主要運用的數學知識包括垂徑定理推論，即垂直于弦（弦非直徑）并平分弦的直線過圓心，以及與圓有關的計算;問題3在新的情境下尋找分配方案，本質上是圓內一點到圓周的最短路徑問題，學生需通過仔細審題，將現實問題抽象為數學問題后再尋求解決方法。

（3）一種思想。基于歷史上的法律問題設計問題串，用數學知識來分析和解決現實問題。在不同的情境下，用數學方法來解釋“就近”原則，體現了數學的模型思想和應用價值，讓學生學會用數學的眼光看待世界，用數學知識解決現實問題，用數學語言描述現實世界。

三、學生反饋

課后，筆者收集了該班25名學生對于本節課的反饋信息。對于“通過這節課，你體會到了學習數學有哪些價值？”這個問題，有18名學生提到了可以利用數學知識解決生活中的實際問題;有6名學生提到了學習數學可以幫助思維更有邏輯性;有1名學生提到了可以用類似的方法解決其他的問題。由此可以看出，數學史融入數學課堂能使學生更深刻地體會到數學的廣泛應用性和嚴謹性。

對于“你認為要解決本節課所遇到的法律問題應遵循怎樣的原則？”這個問題，96的學生提出應遵循公平、公正、可操作的分配原則，由此可以說明，數學史融入課堂教學對學生學習是有意義的。

對于“這節課你印象最深的是什么？為什么？”這個問題，有8名學生提到了用數學知識解決法律問題，認為學習數學知識有實際應用價值;7名學生提到了一題多解，認為問題1的解法多種多樣，很有意思，也讓他們知道解題思路的多樣性;7名學生提到了主要用到了圓的基本性質解決問題，復習了圓的基本性質;3名學生提到了各種分配方案。

四、教學反思

本節課利用淤積地分割問題設計問題串，一方面讓學生在解決問題的過程中整體性復習與圓的性質有關的知識，另一方面，通過問題的不斷改編和層層深入研究，讓學生在不同情境下基于“就近”原則，給出了不同數學解釋，讓學生體會數學的應用價值。

本節課對淤積地分割問題的研究主要可以分為三個階段。第一階段，無原則嘗試分割。課前教師利用學生學習單展示問題，讓學生設計分配方案。課上展示方案，激發學生的學習興趣，讓學生有機會表達自己的觀點，大部分學生的分配分案都是基于自己對問題的理解并用數學知識進行了初步的分割操作，但分割存在無原則或者不好操作的問題。第二階段，初步嘗試按“就近”原則分割。教師展示了歷史上巴托魯斯教授給出的分割原則，并讓學生利用所學知識進行分割，并給出解釋，學生初步用數學的方法解釋“就近”原則，通過教師的設問，初步復習了與圓的性質有關的知識。第三階段，不同情境下的“就近”解讀。問題2和問題3是將淤積地的形狀改變后，讓學生重新用數學的方法解讀已有的分割原則，體會不同情境下“就近”的不同數學解釋，進一步用數學的語言描述現實問題。在將現實問題抽象為數學問題解決的過程中，利用與圓的性質有關的知識解決問題。

不同情境下的分割方案均隱藏著統一的“就近”原則，讓學生體會到解決法律問題時對于公平、公正要求的數學解釋。在利用數學知識解決問題時，讓學生感受到嚴謹的數學精神，感受到做人做事要講“道理”，彰顯了德育之效。

參考文獻：

[1]陳建國.開發教材為素材，演繹復習更精彩：浙教版數學九上《圓的基本性質》復習課教學設計[J].數學教學，2019（6）：6-13.

[2]王海青.論整體主義教學[J].全球教育展望，2019（4）：34-44.

[3]馮銳，劉麗麗.整體論視閾下的教學設計探討[J].開放教育研究，2009（4）：69-73.

[4]丁福珍.整體觀指導下的初中函數單元總復習實踐研究[J].數學通報，2020（4）：47-51.

[5]VAN MAANEN J.Teaching geometry to 11 year old “medieval lawyers”[J].The Mathematical Gazette，1992（475）：37-45.

[6]汪曉勤.一個中世紀法律問題的解決方案和數學教育價值[J].中學數學月刊，2020（1）：42-44.

（責任編輯：陸順演）