永磁輔助同步磁阻電機交直軸電感參數(shù)分析
肖 勇, 陳 彬, 李 霞, 史進飛, 王 杜, 李 瑩
(1.廣東省高速節(jié)能電機系統(tǒng)企業(yè)重點實驗室,廣東 珠海 519070;2.珠海格力電器股份有限公司,廣東 珠海 519070)
0 引 言
永磁輔助同步磁阻電機[1-2]在轉子內放置永磁體,電機的交直軸磁路不對稱,由此產生的磁阻轉矩能否得到充分的利用,與電機的交直軸電感參數(shù)密切相關。因此,在電機設計初期,通過仿真手段精確計算電機的交直軸電感參數(shù)具有重要意義。
目前,相關文獻對永磁電機交直軸電感參數(shù)的計算和仿真方法進行了多方面研究。文獻[3]在瞬態(tài)場中采用增量法計算得到了電機交直軸電感隨電角度的變化曲線。文獻[4-5]利用可計及電樞磁動勢所產生的諧波漏感的繞組函數(shù)法量化分析了分數(shù)槽集中繞組永磁同步電機電感參數(shù)。文獻[6]為減小有限元計算工作量,采用在特定轉子位置下計算電樞繞組交直軸電感的方法。文獻[7-8]采用靜態(tài)場法分析了交直軸電感隨交直軸電流的變化規(guī)律。文獻[9]采用解析法通過公式推導分析了雙繞組永磁同步電機不同嵌線方式對電感的影響。文獻[10]采用集中參數(shù)法研究了飽和對永磁同步電機交軸電感的影響。文獻[11]在非線性B-H數(shù)學模型的基礎上,提出一種新的集總參數(shù)法,以評估內置式永磁同步電機的非線性磁行為。文獻[12]在不同工況下采用保存相對磁導率不變的方法來計算交直軸自感及其交叉耦合電感參數(shù)。
本文以一臺6.8 kW永磁輔助同步磁阻電機為研究對象,采用等效交直軸法、靜態(tài)場法、瞬態(tài)場法和凍結磁導率法進行了電機交直軸電感參數(shù)的仿真計算;試制樣機,并采用伏安法測試了電機電感參數(shù),將仿真結果和實驗結果進行對比,驗證了各仿真方法的準確性。
1 電機模型
以一臺6.8 kW的永磁輔助同步磁阻電機為研究對象,樣機的有限元分析模型如圖1所示。電機主要設計參數(shù)如表1所示。
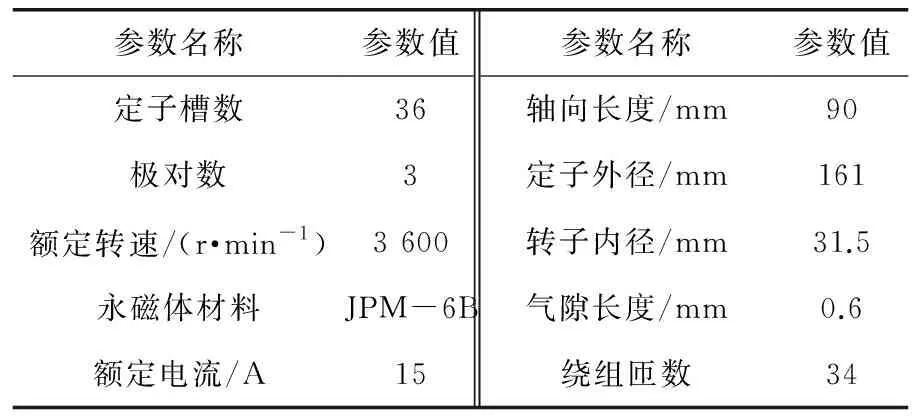
表1 電機參數(shù)
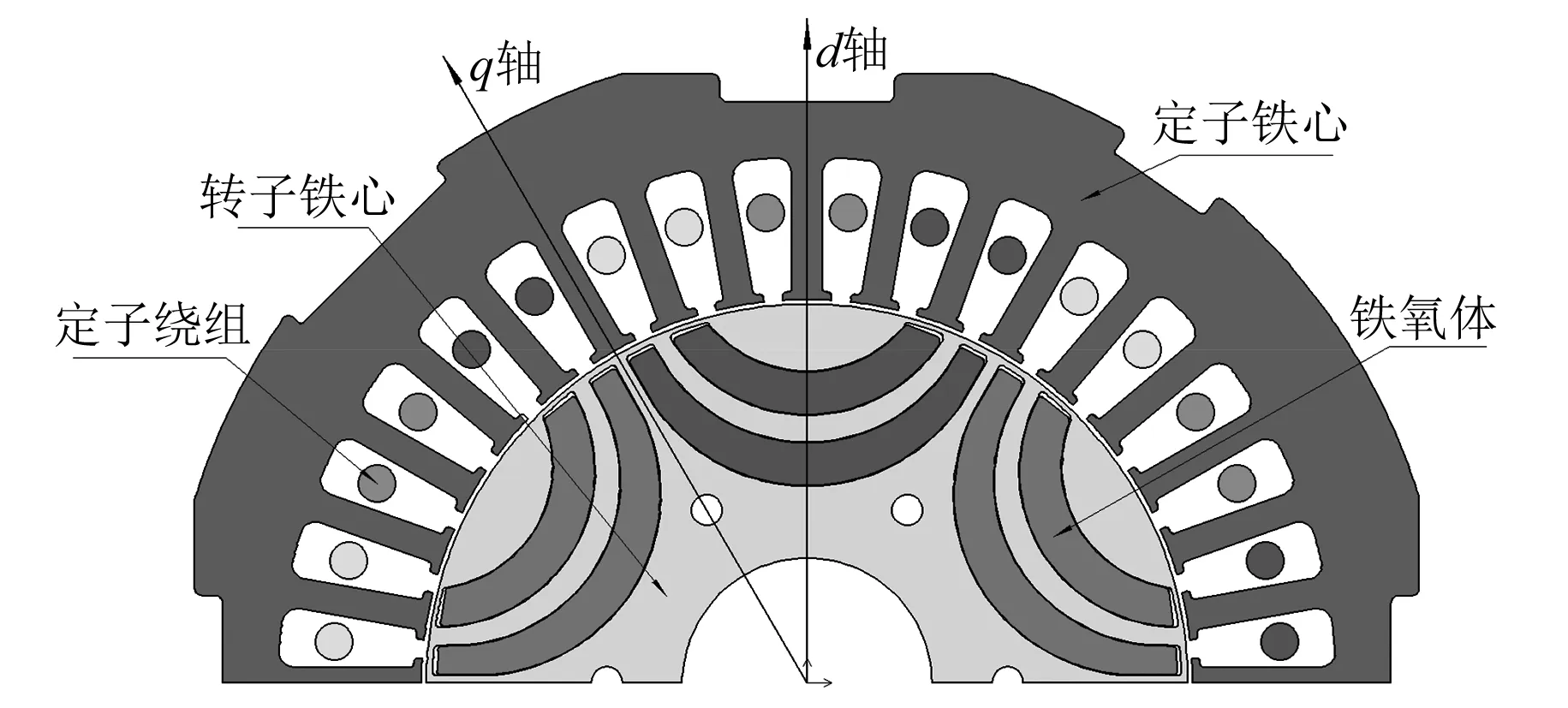
圖1 電機模型
2 等效交直軸法
2.1 等效交直軸法的原理
等效交直軸法是將電機的運行狀態(tài)分解為等
效直軸狀態(tài)和等效交軸狀態(tài)兩種狀態(tài)。等效直軸狀態(tài)即定子磁場方向與轉子磁場方向相同,此時直軸電感的計算公式為
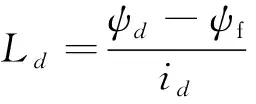
(1)
定子磁場方向與轉子磁場方向垂直時即為等效交軸狀態(tài),此時交軸電感的計算公式為
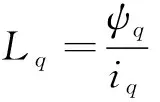
(2)
式中:Ld、Lq為直軸和交軸電感;ψd、ψq為直軸和交軸磁鏈;id、iq為直軸和交軸電流;ψf為永磁體磁鏈。
2.2 等效交直軸法的計算結果
采用等效交直軸法計算得到的不同電流下的交直軸電感如圖2所示。額定電流下電機磁力線和磁密分布如圖3所示。額定電流15 A時,Ld=3.48 mH,Lq=10.85 mH。

圖3 額定電流下電機磁力線和磁密分布
隨著電流的增大,電機飽和程度增加。由圖2可知,交直軸電感值均隨電流增大而減小,其中直軸電感從3.56 mH降至3.45 mH,下降幅度為3.15%;交軸電感從15.96 mH降至8.74 mH,下降幅度為45.22%。交軸電感的變化幅度大于直軸電感,交軸電感對電機的飽和更加敏感。
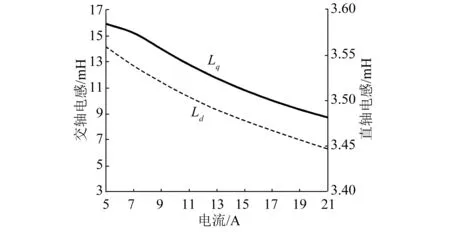
圖2 等效交直軸法電感計算結果
采用等效交直軸法求得的交直軸電感是在弱磁角度為90°或270°以及180°狀態(tài)下,繞組只有交軸磁場分量或直軸磁場分量,未考慮交直軸電流的交叉耦合作用對電感的影響。
3 靜態(tài)場法
3.1 靜態(tài)場法的原理
三相ABC坐標系下,電機的電感矩陣由三相繞組的自感及三相繞組之間的互感構成[13],即:

(3)
要得到交直軸電感參數(shù)的計算公式,需將三相ABC坐標系下的電感矩陣變換到dq坐標系下,變換公式可由定子三相磁鏈的3s-2r變換得出:
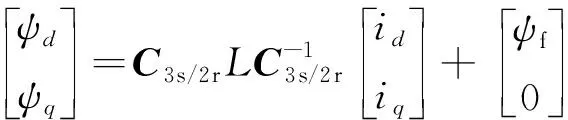
(4)
式中:C3s/2r為三相坐標到旋轉正交坐標變換矩陣。
又因為在dq坐標系下有:
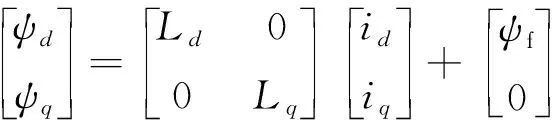
(5)
所以有:
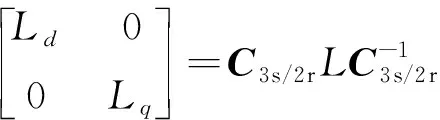
(6)
由式(6)可得直交軸電感的計算公式為
式中:θ為直軸與A相繞組軸線之間的夾角。
3.2 靜態(tài)場法的計算結果
采用靜態(tài)場法計算得到的電機交直軸電感參數(shù)如圖4所示。由圖4可知,隨著電流角的增大,直軸電感減小,交軸電感增大。在額定電流15 A下,交直軸電感的平均值Ld= 4.70 mH,Lq=14.46 mH。
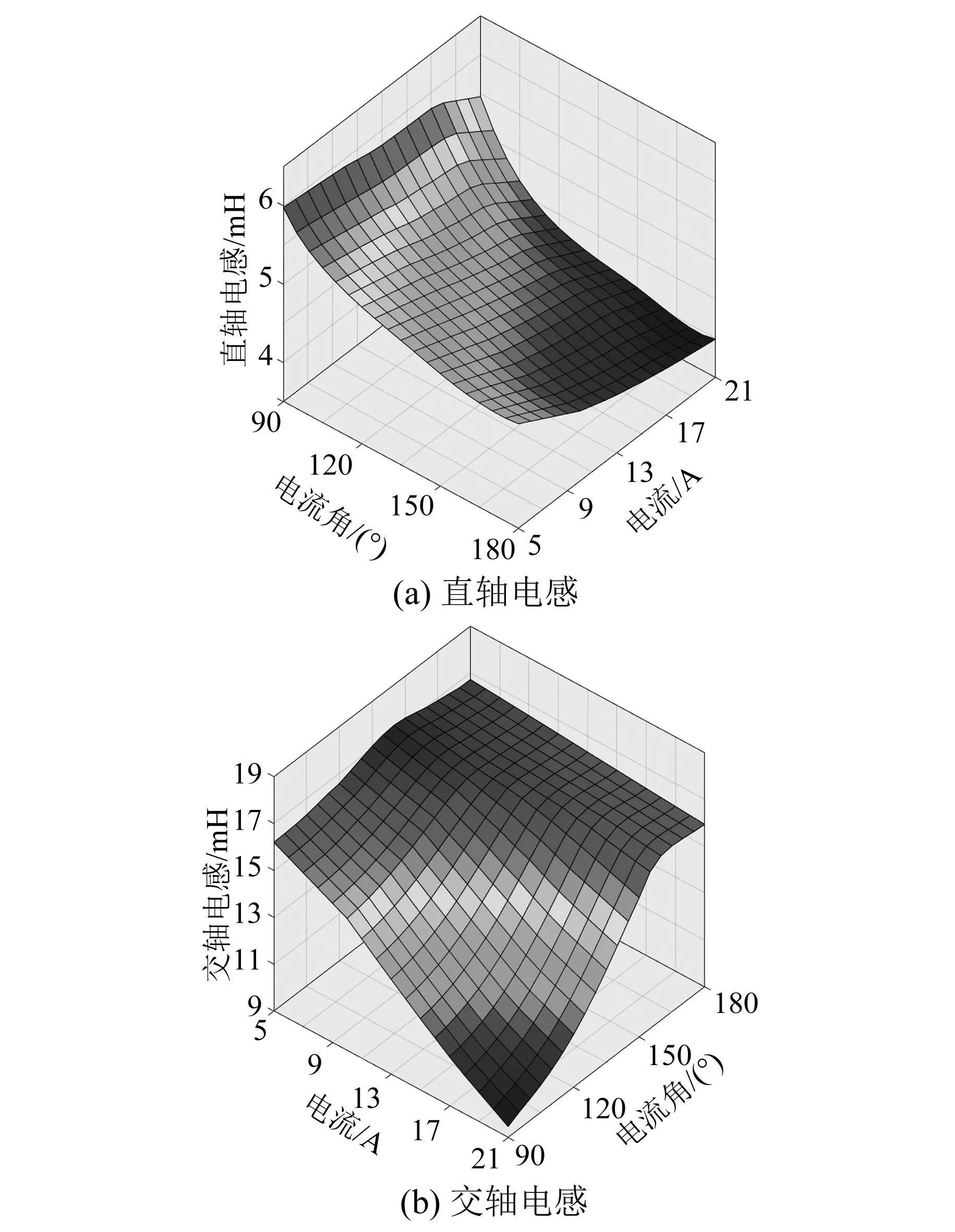
圖4 靜態(tài)場法電感計算結果
固定電流角,分析在只加載直軸電流和只加載交軸電流情況下,交直軸電感變化情況。只加載直軸電流時(電流角為180°),隨著電流的增大,直軸電感從4.84 mH降至3.99 mH,下降幅度為17.56%;交軸電感從16.71 mH降至15.93 mH,下降幅度為4.70%。可以發(fā)現(xiàn),直軸電流的變化對直軸電感的影響更大。
只加載交軸電流時(電流角為90°),隨著電流的增大,直軸電感從5.98 mH降至5.46 mH,下降幅度為8.62%;交軸電感從16.2 mH降至9.47 mH,下降幅度為41.55%。可以發(fā)現(xiàn),交軸電流的變化對交軸電感的影響更大。
4 瞬態(tài)場法
4.1 瞬態(tài)場法的原理
三相電流從ABC坐標到dq坐標的轉換公式為
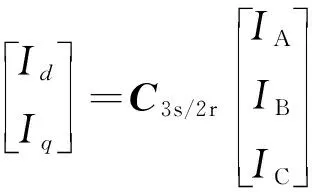
(9)
該公式對三相磁鏈也同樣適用。
在瞬態(tài)場下,給三相繞組施加電流激勵源,可計算得到電機的三相磁鏈值,經(jīng)式(9)變換至dq坐標后得到電機的交直軸磁鏈和交直軸電流,按式(1)和式(2)可計算得到電機的交直軸電感值。
4.2 瞬態(tài)場法的計算結果
圖5所示為瞬態(tài)場法計算得到的額定電流下電機交直軸電感結果。由圖5可知,隨著轉子位置角的變化,交直軸電感均呈現(xiàn)周期性變化,其中直軸電感最大值為3.48 mH,最小值為3.25 mH,變化幅度為6.66%,取平均值為3.35 mH;交軸電感最大值為10.96 mH,最小值為10.62 mH,變化幅度為3.12%,取平均值為10.79 mH。不同電流下計算得到的交直軸電感值如表2所示。
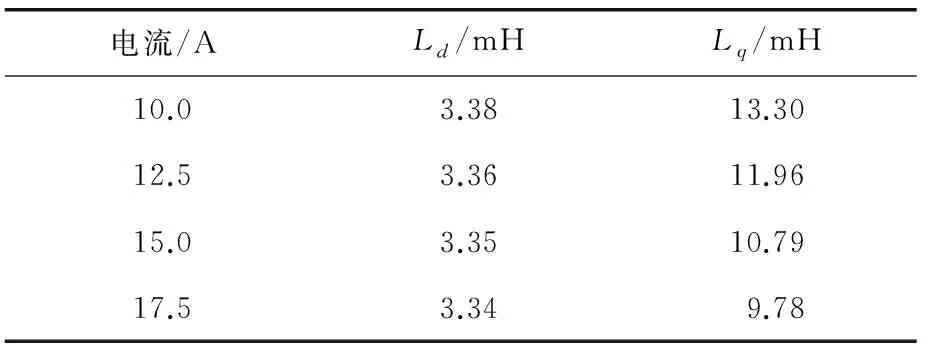
表2 不同電流下交直軸電感計算結果
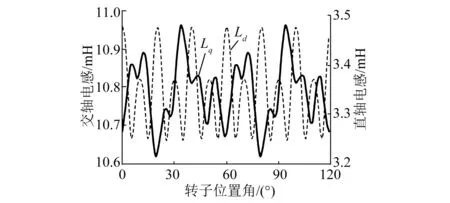
圖5 瞬態(tài)場法電感計算結果
5 凍結磁導率法
5.1 凍結磁導率法的原理
永磁輔助同步磁阻電機運行時,電機內存在由繞組產生的電樞磁場和永磁體產生的永磁磁場。傳統(tǒng)磁鏈模型忽略了交直軸磁路間的交叉耦合作用與磁路飽和作用,認為交直軸磁場正交。為計及磁鏈交叉耦合作用和磁路飽和作用,永磁輔助同步磁阻電機的交直軸磁鏈可以表示為:
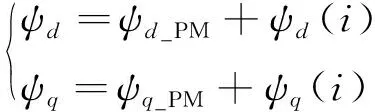
(10)
式中:ψd_PM、ψq_PM、ψd(i)、ψq(i)分別為永磁體和電樞電流產生的交直軸磁鏈。
根據(jù)式(10)可計算得到電機的交直軸電感,計算公式為
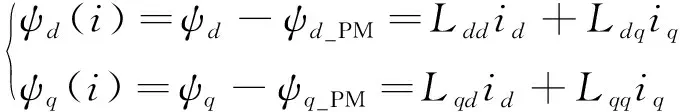
(11)
式中:Ldd、Lqq、id、iq分別為交直軸自感和電流;Ldq為交直軸互感。
根據(jù)式(11)計算電感參數(shù)考慮了交直軸磁路間的交叉耦合作用和磁路飽和作用,該方法需采用凍結磁導率技術[14-15]進行仿真。凍結磁導率技術的原理如圖6所示,具體為:首先仿真負載磁場(A點)得到負載時的磁導率μall,并且將該值存儲在各個單元的數(shù)據(jù)中;然后利用該磁導率分別分析只有永磁體激勵的磁場B(FP,PM)(D點)和只有電流激勵的磁場B(FP,i)(E點),計算得到單獨激勵源下的磁鏈,進而計算得到交直軸電感。
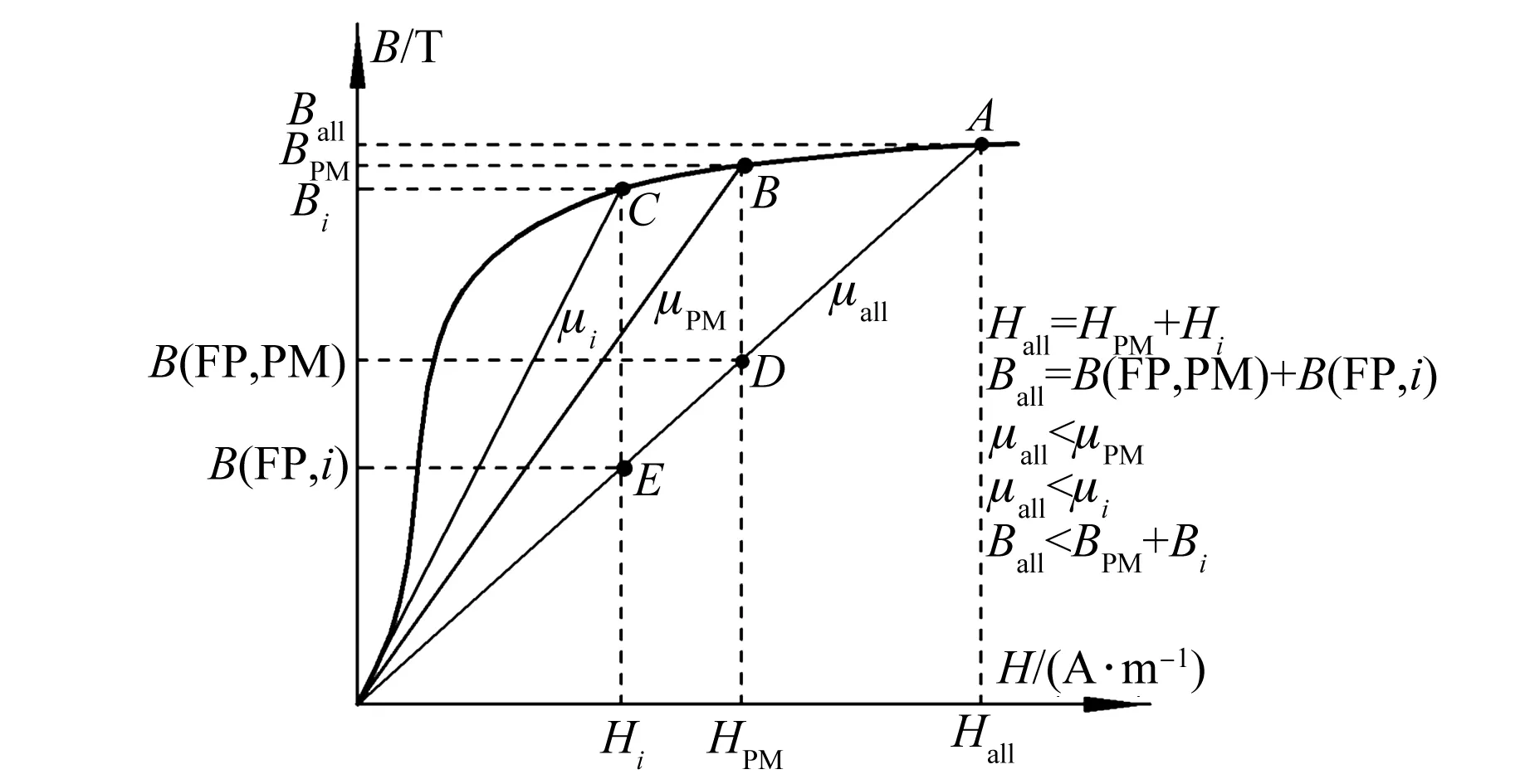
圖6 凍結磁導率技術原理
5.2 凍結磁導率法的計算結果
圖7所示為不同電流下電機相對磁導率云圖,可見電機飽和程度受電流的影響比較大,尤其在定子上更為明顯。圖8所示為凍結磁導率法計算得到的不同電流下的交直軸電感。隨著電流的增大,受電機飽和程度影響,交直軸電感隨轉子位置角的波動幅度增大。額定電流下的交直軸電感值Ld=3.78 mH,Lq=10.48 mH。
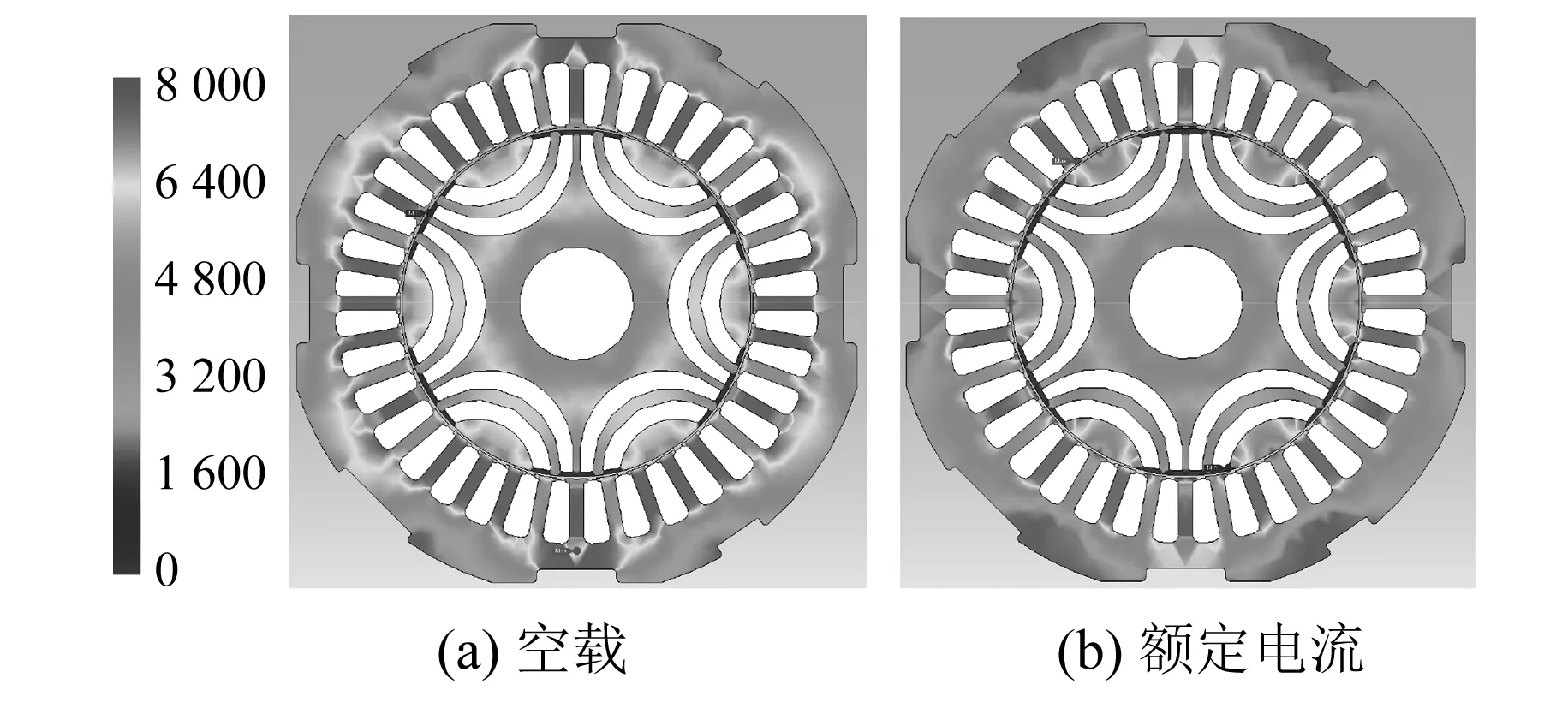
圖7 不同電流下電機相對磁導率云圖
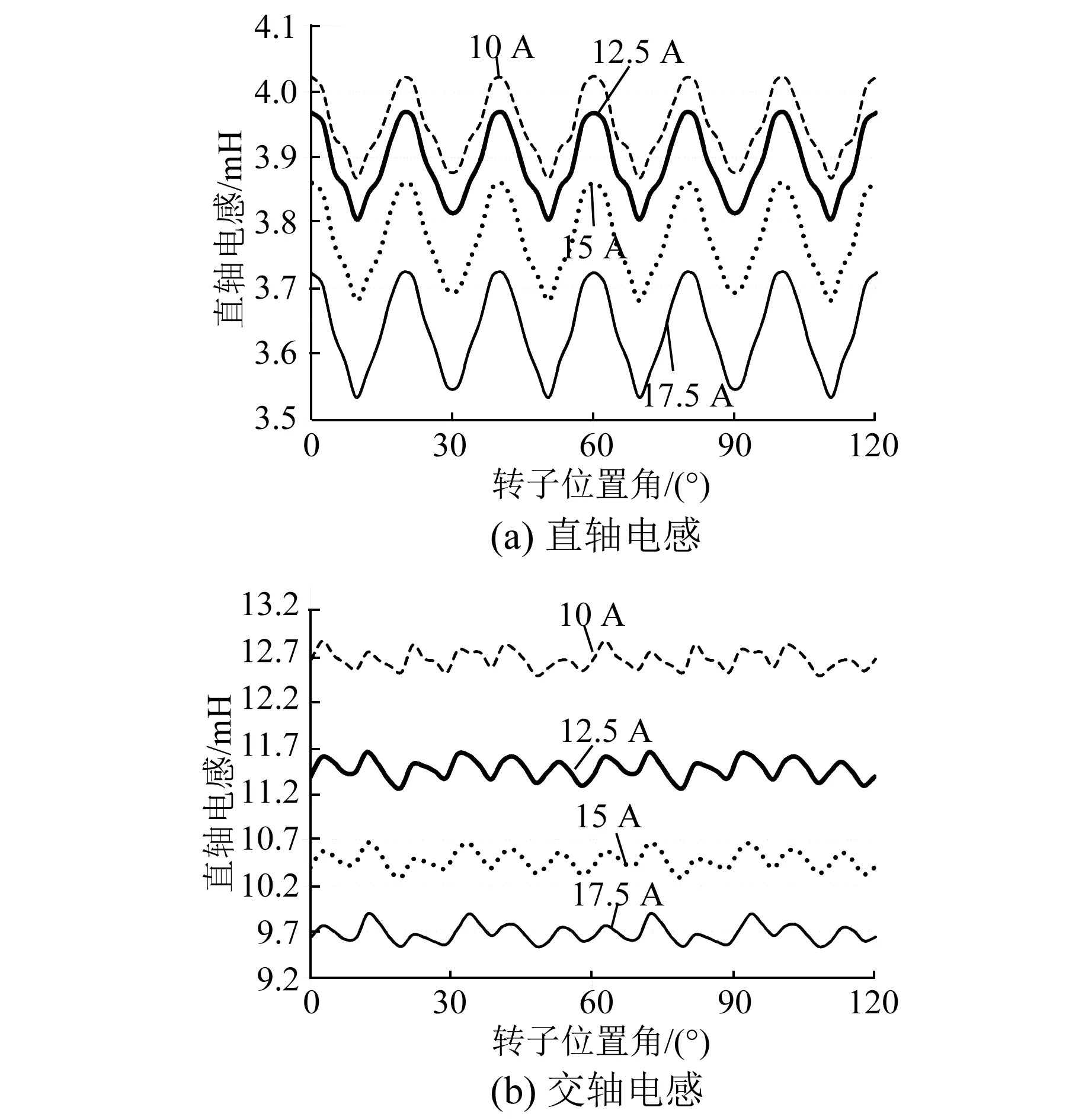
圖8 凍結磁導率法電感計算結果
6 試驗對比
試制樣機并采用伏安法測試了樣機電感參數(shù)。圖9所示為樣機定轉子組件。將等效交直軸法、靜態(tài)場法、瞬態(tài)場法和凍結磁導率法的計算結果與實測結果進行對比,誤差如表3所示,其中凍結磁導率法計算結果與實測結果的誤差最小,且電機飽和程度越高誤差越小,采用凍結磁導率法的計算結果更為準確。

圖9 樣機定轉子組件
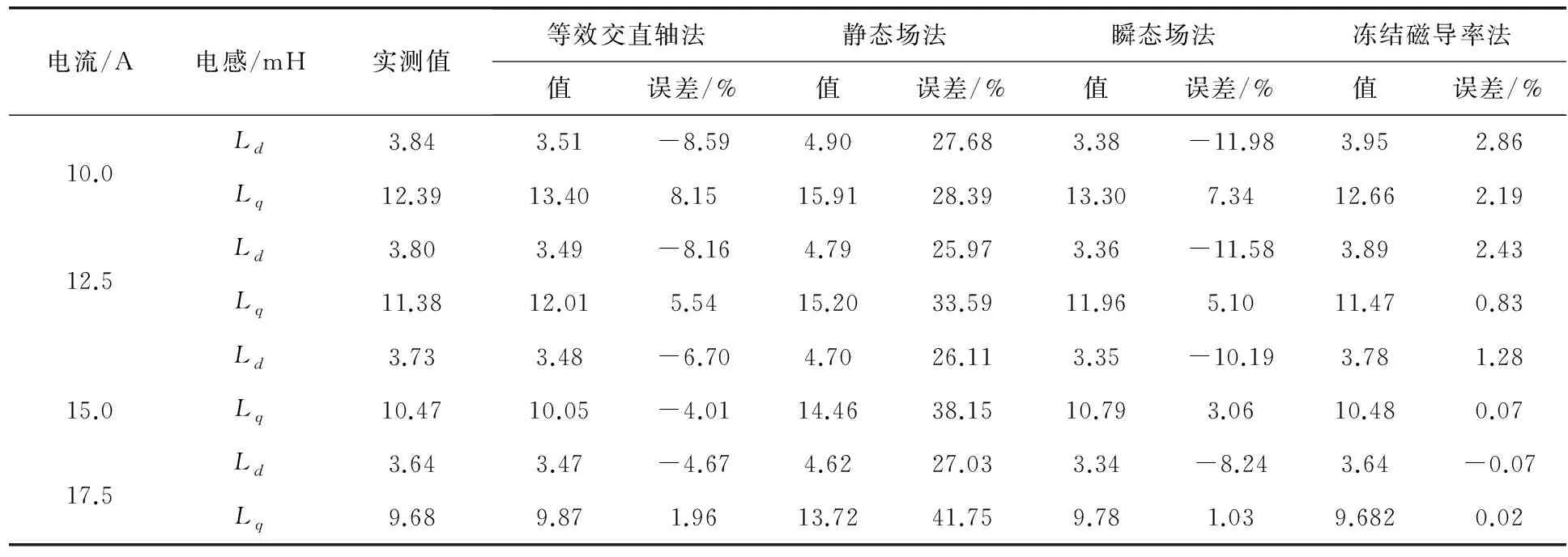
表3 交直軸電感計算結果對比
7 結 語
本文以一臺6.8 kW的永磁輔助同步磁阻電機為研究對象,針對交直軸電感參數(shù)的仿真方法——等效交直軸法、靜態(tài)場法、瞬態(tài)場法、凍結磁導率法,進行了原理介紹和結果對比,結論如下:
(1) 靜態(tài)場法的計算結果與實測結果誤差較大(25%以上),該方法不可取。
(2) 等效交直軸法和瞬態(tài)場法的誤差較靜態(tài)場法小,且隨著電流的增大,誤差呈減小趨勢;對比等效交直軸法和瞬態(tài)場法,采用等效交直軸法計算直軸電感的誤差相對較小,采用瞬態(tài)場法計算交軸電感的誤差相對較小。
(3) 凍結磁導率法計算結果與實測結果的誤差最小且均在3%以內。采用凍結磁導率法計算交直軸電感參數(shù)更為可靠,且該方法更適合電機飽和程度較高時的電感計算。

