悟“數”想“形”，歸“本”求“真”
——一堂“二次函數與一元二次方程”新授課的教學設計與反思

江蘇省太倉市第一中學 (215400) 朱建良

探索數學的本質是數學教學的真諦，學生經歷探究過程，感悟知識的發現發生過程，揭示數學本質才是數學教學的靈魂所在.在日常教學中，教師應回歸教材，在理解教材的基礎上，精心設計問題情境，基于學生的思維而生成拓展新問題，通過剖析問題本質，喚醒學生辯證認識“數”與“形”的內在聯系，通過變式問題引導學生自覺探究思辨，生成經驗.本文筆者結合教學案例談談新授課中嘗試引導學生感悟問題本質，獲得認知數學方法的一些理解，以求拋磚引玉.

1.教學分析

1.1 教材解析

教學內容為蘇科版九年級上冊§5.4 二次函數與一元二次方程(第1課時)，§5.1-5.3所學的二次函數是初中數學教學的重難點，本課時借助二次函數圖像解決一元二次方程求根問題，其方法比較抽象，要求學生積累抽象函數本質特征所需的知識和經驗，要求會用數形結合的方法解決問題，本節課揭示了方程、函數、不等式之間的內在聯系，為后階段高中數學學習起著承前啟后的橋梁作用.

1.2 學情分析

九年級學生接受能力強，思維活躍，具備了一定的數學探究活動經歷，學生已經掌握了不同類型的方程的解法及其應用，掌握了研究函數的圖像和性質以及函數的應用的一般方法，有較強的推理分析能力，為順利完成本課學習打下了扎實的基礎.從學生有待于提高的知識和技能來看，嘗試通過探索函數與方程關系，感受“對立統一”的唯物辯證法，通過由圖像求方程的根的探索活動，培養學生“數形結合”探討問題的研究能力.

1.3 教學目標

(1)理解二次函數與x軸交點的個數與一元二次方程的根的個數之間的關系；

(2)能夠根據二次函數的圖像與x軸的交點情況判斷相應的一元二次方程根的情況；

(3)理解二次函數、一元二次方程之間的相互聯系，用對立統一的辯證觀點體會數形結合思想的應用.

1.4 教學重點

應用一元二次方程根的判斷式及求根公式，對二次函數圖像進行再研究，并結合二次函數圖像加以記憶，基于通過“形”的視角，理解二次函數和一元二次方程的內在聯系，學會從二次函數圖像深度理解一元二次方程根的幾何特征.

2.教學設計簡析

2.1 知識連接點處，明晰概念

教育價值是教學設計的靈魂，也是教學邏輯的起點，提出一次函數與一元一次方程的辨析反思問題.在困惑思辨中，引導學生產生疑問，產生認知沖突，提出的問題從字母x表示的意義入手，問題驅動思考，直擊數學本質，即函數研究變量x與y的對應關系，方程研究未知與已知量之間的相等關系，求方程解.

(2)一次函數y=kx+b(k≠0)、關于x的一元一次方程kx+b=0(k≠0)分別建立了哪些量之間的關系？它們各自考慮問題的出發點有什么不同？

(3)一次函數與一元一次方程存在什么聯系？

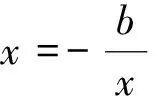
教后反思：一次函數中x表示未知數，函數刻畫的是變量x、y的變化規律，方程尋求的是相等關系下未知數與已知量之間的數量關系，即方程的解，在概念辨析中挖掘研究對象的問題價值，尊重學生的認知，圍繞學習目標，關注了思維價值.問題1低起點、緩坡度，較好地體現了函數、方程與不等式之間的關系 ,突出了新課程注重基礎、關注聯系與綜合的特點.

2.2 經驗連接點處，經歷轉化

通過類比，巧妙過渡，順理成章地運用解決一次函數與一元一次方程數形結合的方法，分別研究二次函數y=x2-2x-3，y=x2-2x+1，y=x2-2x+2圖象與x軸交點坐標與分別相對應的一元二次方程x2-2x-3=0，x2-2x+1=0，x2-2x+2=0的根的情況，從學生已有的認知，活動經驗出發，化復雜為簡單，化未知為已知，用數形結合的經驗即利用拋物線與x軸交點的個數來判定相對應的一元二次方程解的情況，從整體關聯的視角認識一元二次方程與二次函數聯系.

問題2 分別在三個平面直角坐標系中，畫出二次函數y=x2-2x-3、y=x2-2x+1、y=x2-2x+2的圖像.觀察思考：

(1)分別判斷一元二次方程x2-2x-3=0、x2-2x+1=0、x2-2x+2=0根的情況？

(2)你能利用圖像解析一元二次方程的根的不同情況嗎？

(3)二次函數y=ax2+bx+c(a≠0)的圖像和x軸交點的坐標與關于x的一元二次方程ax2+bx+c=0(a≠0)的根有什么關系？

解析：(1)分別計算根的判別式△；(2)鑒別關注拋物線與x軸交點的個數；(3)當△>0時，分別對應該一元二次方程有兩個不相等的實數根，當△=0時，有兩個相等的實數根，當△<0時，沒有實數根.

教后反思：判斷一元二次方程根的情況，引導學生怎么想到利用圖像法判斷？為什么要這樣？一定要這樣嗎？有方法層面比較后的思考嗎？引導學生自主建構增強學生的應用意識,，同時把數形結合思想反映得淋漓盡致，數學課堂知識、方法、結構如下圖.

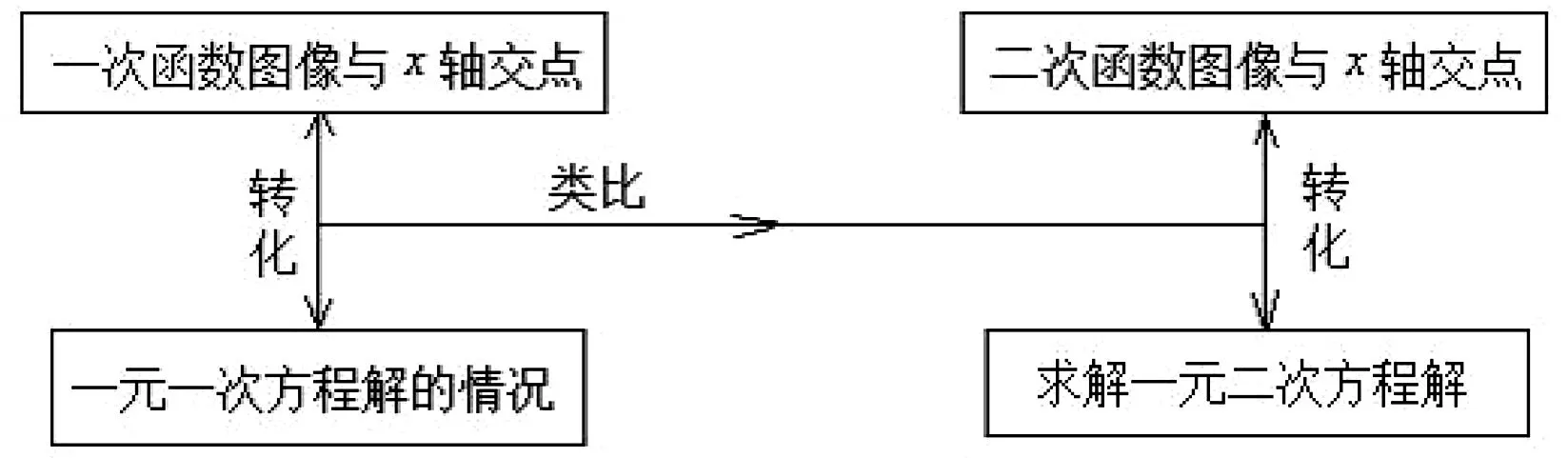
2.3數形結合，優化思維

看“形”思“數”，見“數”想“形”.把握學生思維的切入點，啟發學生自己畫出拋物線并觀察思考，如何確定二次函數y值的非負性，關鍵取決于對y=ax2+bx+c中的系數a的符號判定，及△=b2-4ac的值，在分類討論中，真正理解一元二次方程根的幾何意義，實質就是以“數”化“形”，嘗試從函數內部特征挖掘出有價值的新問題，揭示出函數、方程之間的聯系.

問題3 已知二次函數y=ax2+bx+c(a≠0)及其分別對應的圖像如圖1，圖2，圖3，對稱軸為直線x=3.

圖1 圖2 圖3

(1)觀察三個圖像，設y=0，分別觀察拋物線上縱坐標為0的點在哪里？你能解關于x的一元二次方程ax2+bx+c=0嗎？如圖3，若關于x的一元二次方程ax2+bx+c-m=0有兩個不相等的實數根，求m的取值范圍？

(2)類比上述問題，請提出新問題探究討論.

解析：當x=3時，ymax=-1，即m<-1，也可轉化為ax2+bx+c=m，研究拋物線y=ax2+bx+c與直線y=m的交點入手，研究交點坐標的意義，也可通過平移拋物線y=ax2+bx+c-m的角度討論m的取值范圍.此問題也可變式為：關于x的一元二次方程ax2+bx+c-m=0有實數解，求m的最大值？

教學反思：讀懂圖中有效信息，展開對比式訓練, 拉近點狀知識間的距離, 尋找不同問題之間的內在聯系，讓學生感悟研究問題的方法不變，從函數、方程、不等式的角度，在自然的探究活動中體會到其中內涵，這種由淺入深、由易到難,，循序漸進的設計中，學生整體感受了其內在聯系，“類比“和“抽象”的思想也得到了自然滲透.

2.4 沉淀思維，提煉方法

變式問題，螺旋式遞進，設計拋物線y=x2-4x+k+2與x軸交點問題的變化，引發學生思考，依據條件，嘗試構造圖形，由“形”的直觀變為“數”的嚴密，巧妙轉化，探求結論，以“數”化“形”，以“形”變“數”相結合，關注在探究活動中生成的問題，聚焦在解決問題時學生產生的疑惑.

問題4 已知二次函數y=x2-4x+k+2，若該二次函數的圖像與x軸有公共點，求k的取值范圍？

此題易解且有如下變形：

變式1k為何值時，該二次函數的圖像與坐標軸有兩個交點？

變式2k為何值時，該二次函數的圖像與x軸兩交點間的距離為2？

變式3k為何值時，該二次函數圖像頂點到x軸的距離為2？

拓展1 若二次函數y=x2-4x+k+2的值恒大于零，求k的取值范圍？

拓展2k為何值時，拋物線y=x2-4x+k+2與直線y=x-1只有一個交點？

教學反思：由拋物線y=x2-4x+k+2與x軸的交點問題的討論拓展到該拋物線與直線y=x-1交點問題的研究，再次強化逐步分解問題，關注解決問題的方法策略，即拋物線與x軸有無交點，怎樣通過交點問題研究一元二次方程的解，讓學生的數學理解逐步深刻，由低價思維走向高階思維，思維訓練拾級而上.

2.5 延伸探究，鞏固提升

深度學習是一個由薄到厚，再由厚到薄的再創造過程，在明晰求解一元二次方程解的基礎上，類比相關概念，尋找解決問題的突破口，正確理解拋物線與x軸交點所對應的一元二次方程解的內在聯系.

問題5(1)函數y=ax2+bx+c(a≠0)與y=x的圖像如圖4所示，以下結論正確的是：①b2-4c>0；②b+c+1=0；③ 3b+c+6=0；④ 當1

圖4

(2)已知點A(1,1)在二次函數y=x2-2ax+b的圖像上.

①用含a的代數式表示b；②如果該二次函數的圖像與x軸只有一個交點，求這個二次函數的圖像的頂點坐標.

解析：(1)③、④；(2)①b=2a，(2)②y=x2-2ax+2a，當a=0時，y=x2，頂點(0,0)，△=4a2-8a=0，當a=2時，y=x2-4x+4，頂點(2,0).

教學反思：通過延伸探究，整合函數知識體系，強化對方程求解問題表征的理解.充分利用拋物線、直線的性質和幾何意義，把“形”正確表示成“數”的形式，然后進行推理計算，優化重組原有知識結構.

3.教學反思

3.1從溯源開始，揭示本質

本課例從分析函數圖像上特殊點對應的坐標特征入手，從學生已有的函數認知水平出發，由淺入深，由表及里，尋求一元二次方程的解，類比抽象出一般方法，引導學生深刻理解由函數圖像生成求方程根的方法，領悟二次函數圖像與x軸交點的結構關系本質，問題設計層次感強，探究路徑清晰，既重視了數學知識階段學習的梳理與歸納，也注重了學生數學思維的啟發和點撥，突出了崇尚嚴謹推理和理性思考的精神風貌.

3.2從“雙基”向“四基”轉變，引領探究過程

義務教育課程目標強化了課堂學習要發展學生的能力性目標，本課例的問題設計從一次函數與一元一次方程的聯系類比到二次函數與一元二次方程的聯系，在學生認知困惑處設疑問難，深刻理解二次函數圖像和性質.梳理特殊點的坐標與方程解的對應關系，探究出函數、方程、不等式三者之間的內在聯系，問題的設計遵循啟發性原則，讓學生經歷數學知識的發展、發生過程，在有效探究活動中，讓學生深刻體會一般與特殊，數形結合，轉化等數學思想，抽絲剝繭般的問題串驅動學生綜合所學的知識去理解函數思想、方程思想，并分析和解決問題，由此提升學生的數學素養.

3.3從“理解教學”入手，有效銜接“教”與“學”

本課例關注了教學內容“數”與“形”相融的特點，關注學生對函數圖像的認知現實，注重學生的自主探究與教師引導的相互滲透和互相促進，基于拋物線與x軸交點形態設計問題，通過平移拋物線變化交點坐標位置，深化問題，拓展思維空間，引導學生學會自主探究二次函數圖像與x軸交點的幾何特征，學會轉化，學會從“數”與“形”的視角深刻理解二次函數與一元二次方程之間的橫向聯系，掌握從函數圖像的視角去解決求方程解的方法.深刻理解感悟一元二次方程的根可能出現不同情況的原因，并提煉出關于一元二次方程的根可能出現情況的幾何形態的解釋，教學設計循序漸進，問題引領下的“學”更具研究性和發展性，提升了學生的研究能力.

本課例以數學知識的發展過程和學生認知發展的心理過程為主線，構建了過程性的探究活動，學生在建構數學知識的過程中學會發現和分析問題，學生在思考、交流、發現、理解中剖析問題本質，學會了借助形的幾何直觀性來刻畫闡述數之間的某種數量關系，深刻理解了“以形助數”或“以數解形”的內涵，使復雜問題簡單化，抽象問題具體化，開拓了學生的思維視野.