2-UPS/RPR并聯機構運動學分析

周毅鈞,陳建鵬,李特奇

(安徽理工大學 機械工程學院，安徽 淮南 232001)

2R1T少自由度并聯機構由運動副與各個構件組成，其結構較為簡單，因此具有載荷比高、誤差小、精度高、動力充足等優點，且相對傳統串聯機構更有效，結構更緊湊，適用于工業生產、產品分揀等領域。針對2R1T少自由度機構,趙傳森等提出了一種2-RPU/RPS并聯機構,并求出其工作空間與奇異位形；李清等提出了一種SPR+UPS+UPR非對稱并聯機構，并利用三維動態法求解其工作空間；楊路等提出了一種2-UPS/RRP機構，并分析其運動學性能；王新宇等提出了一種2-PSR/UPU并聯機構，并進行實例分析；張志良等提出一種3-PSP空間并聯機構，并利用位置正逆解求其空間位置。研究提出的2-UPS/RPR并聯機構可以用于貼碼的噴涂。傳統貼碼噴涂由于其結構的限制，只適用于噴涂固定表面以及位置不變的產品，而本機構具有兩轉動一平移3個自由度，可適用于曲面等非平面產品的光滑噴涂。

1 機構的結構分析

1.1 機構描述

2-UPS/RPR并聯機構由定平臺、動平臺、虎克副、移動副、球副、轉動副組成，定平臺與動平臺之間通過兩條UPS支鏈和一條RPR支鏈連接。UPS支鏈自下而上依次為虎克副(U)、移動副(P)、球副(S)。以第一條支鏈為例，虎克副(U)與定平臺之間成一定的夾角，定平臺與虎克副(U)相連，虎克副(U)上方連接一個方向向上的移動副(P)，移動副(P)上連接一個球副(S)，球副(S)與動平臺相連。定平臺是底邊邊長為2a,頂角為90°的等腰直角三角形。動平臺是底邊邊長為2b的等腰直角三角形(b并聯機構的模型圖如圖1所示。由圖1可知，并聯機構共有3條支鏈，其中底邊兩條支鏈為相同的UPS支鏈，頂邊為RPR支鏈，RPR支鏈中兩個R副空間位置相互垂直。為了方便分析該機構的正反解，規定定平臺左端頂點為

A

，逆時針分布得到

A

、

A

；動平臺左端頂點為

B

，逆時針分布得到

B

、

B

。其中，

A

、

A

、

A

分別為

U

、

U

、

R

的質心點；

B

、

B

、

B

分別為

S

、

S

、

R

的質心點。以定平臺底邊中心為定坐標系原點建立坐標系

o

-

xyz

，

x

軸與定平臺底邊重合，

x

軸方向指向第二條支鏈底端

U

的質心處，

z

軸方向與定平臺方向垂直，

y

軸方向由右手螺旋定則確定；以動平臺底邊中心為動坐標系原點建立坐標系

o

-

x

y

z

,

x

軸與動平臺底邊重合，方向指向第二條支鏈頂端

S

的質心處，

z

軸方向與動平臺方向垂直，

y

軸與動平臺高重合，方向指向動平臺頂點，

x

軸根據右手螺旋定則確定。2-UPS/RPR機構簡圖如圖2所示。

圖1 2-UPS/RPR機構模型圖2 2-UPS/RPR機構簡圖

1.2 自由度運算

給定螺旋

$

=(

L

,

M

,

N

;

P

,

Q

,

R

)與螺旋

$

=(

L

,

M

,

N

;

P

,

Q

,

R

),則兩螺旋的互易積表示為：

$

○

$

=

L

P

+

M

Q

+

N

R

+

L

P

+

M

Q

+

N

R

,

(1)

若兩螺旋的互易積為0，則兩螺旋互為反螺旋。在并聯機構中，各分支運動螺旋數目與其對應的約束螺旋數目之和為6。對于2-UPS/RPR并聯機構，先求得3條支鏈的運動螺旋系，然后根據互易積理論可得到與其對應的約束螺旋系，接著將3條支鏈的約束螺旋系合并后得到動平臺的約束螺旋系，最后對其求反螺旋系，從而得到動平臺的運動螺旋系。

第一條UPS支鏈共有6個運動螺旋，組成的運動螺旋系可表示為：

(2)

式中，

l

、

m

、

n

中的

ij

表示第

i

條支鏈的第

j

個運動副;

l

表示該運動副位置矢量的方向余弦;

X

1、

Y

1、

Z

1為

$

的位置矢量。從式(2)中還可看出，UPS支鏈的6個運動螺旋線性無關，因此該運動螺旋系不存在與之對應的約束螺旋系，即該支鏈對動平臺無約束力與約束力偶。第二條支鏈的構型與第一條支鏈構型相同，且相對于機構幾何中心點呈對稱分布，因此第二條支鏈也無約束螺旋系。

第三條RPR支鏈在定坐標系中的運動螺旋為：

(3)

根據互易積公式，RPR支鏈的約束螺旋系有3個約束螺旋：

(4)

根據3條支鏈的約束螺旋系得到動平臺的運動螺旋系為：

(5)

如果機構中運動螺旋數目超過6，則超出部分為并聯冗余約束，所以過去常用的Grübler-Kutzbach(以下簡稱G-K)公式無法對所有機構求得正確的結果，因此對G-K公式加以修正,修正后G-K公式如式(6)所示。

(6)

式中,

dof

為機構自由度；

m

為剛體自由度;

N

為構件數量(定平臺也看作為一個構件)；

J

為關節的數目；

f

為第

i

個關節的自由度數;

ζ

為機構中全部過約束的總數;

υ

表示并聯冗余約束;本機構屬于單環機構，因此無并聯冗余。對于2-UPS/RPR并聯機構，

m

與

λ

之和為6，公共約束

λ

=0，即

m

=6-

λ

=6，構件數量

N

=11，關節數目

J

=12。其中轉動副的自由度為1，移動副的自由度為1?；⒖烁钡淖杂啥葹?，冗余自由度

υ

=0，過約束自由度

ζ

=0。將其代入修正的G-K公式可得：

dof

=6×(11-12-1)+(6×2+3)+0-0=3，

由G-K公式計算得出2-UPS/RPR并聯機構的自由度為3，與螺旋理論計算出的結果一致。

2 機構的運動分析

2.1 位置反解

在動平臺位姿確定后求其他構件運動狀態為位置反解。將動平臺中心點的位置設為

P

，因機構只能繞

x

、

y

軸轉動，沿

z

軸移動，所以3個姿態角中繞

z

軸轉動的角度

γ

為0，設繞

x

軸轉動的角度為

α

，繞

y

軸轉動的角度為

β

，根據以上參數可求得支鏈上的3個驅動副的位移距離。

(7)

將動坐標系原點

O

表示為定坐標系中的坐標矢量

P

：

P

=(

x

,

y

,

z

),

(8)

(9)

式中,

s

表示

sin

；

c

表示

cos

。動平臺在固定坐標系中的坐標矢量為

OB

，將

OA

與

OB

的矢量差長度設為

l

，可得：

(10)

l

=|

OB

-

OA

|,

(11)

代入計算得：

(12)

2.2 位置正解

位置正解即根據驅動值求解動平臺中心點位置參數，該方法是位置反解的一種逆運用。本例為一般構型，采用方法為數值分析法，將位置反解方程式整理得到動平臺坐標系原點位置的求解方程：

(13)

該方程為多元非齊次線性方程，常規求根公式無法求得該方程的解析解，但該方程在單根附近平方收斂，因此采用牛頓-拉夫遜迭代法對函數進行更新迭代，從而求得近似解，牛頓迭代公式如下：

(14)

已知3個移動副伸縮量

l

、

l

、

l

，初始向量

T

，經過不斷更新迭代后得到最終向量

T

，同時計算得到3條支鏈移動副移動的距離，該方法可求得動平臺最終的位姿變化。

3 速度雅可比矩陣分析

選取并聯機構3條支鏈的移動副作為驅動向動平臺輸入速度，輸出速度由雅可比矩陣來映射到動平臺上。將位置逆解分別對

α

、

β

、

z

求一階導數，求得的參數代入雅可比矩陣中，雅可比矩陣

J

為：

(15)

其中,

(16)

對位置逆解方程兩側同時求導并加以整理得到：

(17)

4 運動學仿真

為了分析2-UPS/RPR機構在輸入3個驅動函數下動平臺變化的規律，在3條支鏈上的3個移動副設置驅動函數進行驅動，驅動函數如下：

(18)

設定仿真時間為30 s,步數為500，機構開始運動后得到動平臺運動仿真曲線云圖。位移、角速度、速度、加速度變化曲線圖分別如圖3、圖4、圖5、圖6所示。由圖3、圖4可知，Adams仿真云圖呈周期性變化，周期為12.5 s，動平臺在

x

軸方向位移變化較小，角速度變化較大；在

y

軸方向位移變化較大，角速度變化較小。由圖5、圖6可知，動平臺在

z

軸方向速度與加速度變化高于

x

軸、

y

軸。因為

z

軸為移動，另外兩軸為轉動，而移動副行程較長，從位置反解中也能體現出角度變化率比桿長變化率小?？傮w來看，動平臺參數變化曲線光滑連續，中間無斷點與突變，表明機構能平穩運行。綜上，2-UPS/RPR并聯機構的運動性能良好。

圖3 位移變化曲線圖

圖4 角速度變化曲線圖

圖5 速度變化曲線圖

圖6 加速度變化曲線圖

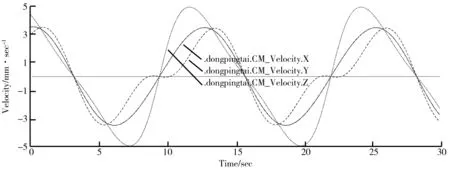
5 結論

基于螺旋理論求得2-UPS/RPR并聯機構存在繞

x

軸、

y

軸轉動與沿

z

軸移動自由度，表明該機構可調節不同角度對不規則曲面產品進行噴涂。運用封閉矢量法與坐標轉換法求得并聯機構反解方程與正解方程，對其運用微分法求得雅可比矩陣，從而得到其運動學特性。利用Adams動態仿真得出機構的運動變化曲線圖，從曲線良好的運動學性能可看出該機構在進行噴涂工作時平穩流暢，具有一定的實用價值。