基于網絡視角的國際銀行間市場波動性溢出效應研究

宋琴 方文 甘珂

摘? ?要：本文選取2007年3月—2020年6月美元、歐元、英鎊、日元和人民幣三個月LIBOR-OIS和SHIBOR-OIS數據，運用VARMA-AGARCH模型，采用網絡拓撲分析法，研究美國、歐元區、英國、中國以及日本銀行間市場波動性溢出效應，并構建波動性溢出指數。研究發現：國際銀行間市場存在顯著的波動性溢出效應，條件波動率不僅受到自身市場前期沖擊和波動影響，還會受到其他市場干擾;金融危機和新冠肺炎疫情暴發期間，國際銀行間市場波動性溢出效應均顯著增強，并呈現動態特征;美國對其他經濟體銀行間市場波動性溢出最大，且在危機時期急劇上升，因此，中國銀行間市場監管要防范境外市場風險跨區域傳遞，尤其是美國市場波動的輸入性沖擊。

關鍵詞：國際銀行間市場;VARMA-AGARCH模型;波動性溢出矩陣

中圖分類號：F830.3? 文獻標識碼：A? 文章編號：1674-2265（2021）06-0070-08

DOI：10.19647/j.cnki.37-1462/f.2021.06.009

一、引言

現代金融系統呈現出復雜的網絡特征，傳統的“太大而不能倒”的原則，逐步轉向 “太關聯而不能倒”的理念。在開放經濟中，市場沖擊通過金融傳染，傳導至不同國家，易形成“發生—傳導—再傳導”循環。從20世紀的大蕭條到2008年的全球金融危機，以銀行為代表的金融機構在金融風險傳染過程中發揮的作用，尤其是波動性溢出效應更是越來越受到理論界和實務界廣泛關注。

在中國金融體系中，銀行是主導機構，銀行間市場是核心的基礎市場。劉沖和盤宇章（2013）[1]認為銀行間市場和實體行業存在雙向反饋機制，并且會影響實體經濟的健康發展。《中國金融監管報告2018》認為中國金融體系的系統性風險主要來自三個根源：一是來自中國宏觀經濟周期性或結構性變化對金融體系產生的系統性沖擊;二是來自金融體系內部的自身演化和逐步累積的風險;三是來自中國經濟金融體系之外的外部風險溢出，主要是國際金融市場的影響。近年來，中國金融市場開放程度逐步擴大，銀行間市場與其他經濟體聯系愈發緊密。金融風險跨區域傳遞以及境外市場的波動性溢出會對本國市場產生沖擊，對中國金融監管提出新要求。

因此，本文依據SDR貨幣籃子選取原則，對由美國、歐元區、英國、中國、日本等經濟體所組成的國際銀行間市場進行實證研究。在此基礎上，運用VARMA-AGARCH模型研究各國市場的波動性溢出效應，并采用網絡拓撲分析法構建波動性溢出指數，來衡量銀行間市場的波動性溢出程度，以正確評估中國在全球風險傳遞鏈中的角色和地位。同時，本文還分析以新冠肺炎疫情為代表的突發性公共衛生事件對國際銀行間市場波動性溢出效應的影響，從而為主動應對外部沖擊、保持金融穩定與安全提供重要的參考依據。

二、文獻綜述

經濟全球化使得全球金融市場的關聯愈發緊密，世界各國逐漸重視跨境市場的風險傳染效應。Dornbusch等（2000）[2]認為金融風險傳染是由金融市場關聯性所導致的傳染，通常指單一國家金融市場沖擊基于市場之間的聯系向其他國家傳遞的現象。Forbes和Rigobon（2002）[3]在總結了前人對亞洲金融危機時期股票市場的研究后，將金融風險傳染效應定義為在市場劇烈動蕩時期跨市場的相關性明顯增強的過程。世界銀行將金融風險傳染分為廣義傳染、嚴格傳染和十分嚴格傳染三個層次。廣義傳染指單一市場波動會傳遞至其他市場，從而引發系統性風險，即波動性溢出效應，該效應無論在經濟危機時期還是經濟平穩時期均存在，也是在跨境風險防范中最需要注意的部分。

2008年金融危機之后，越來越多的學者注重對波動性溢出效應的研究，進而為建立完善的風險預警機制提供思路。張兵等（2010）[4]等通過對中美股票市場聯動性的研究發現，在QDII實施之后，美國股市對中國股市的開盤價和收盤價均有顯著的引導作用。 Balli等（2015）[5]對2000—2013年美國、歐洲、日本等發達經濟體股票市場對亞洲、中東、北美等區域20個新興國家股票市場溢出效應進行研究，發現發達經濟體對新興市場存在顯著的溢出效應，尤其是美國的溢出占據主導地位。此外，溢出效應的程度受到兩國之間貿易規模、投資規模以及地理距離等因素的影響。

除了股票市場之外，銀行間市場也具有波動性溢出特征，Ribeiro和Curto （2017）[6]以LIBOR-OIS利差作為代理變量，采用多元GARCH模型，研究發現美國、歐元區、英國、瑞士以及日本等發達經濟體銀行間貨幣市場之間存在顯著的相關性和波動性溢出效應，并且呈現非對稱的特征，即負向沖擊的影響顯著大于正向沖擊。對于銀行間市場的波動性溢出渠道，Allen和Gale（2000）[7]研究認為金融風險會通過銀行間的債權債務關系進行傳遞，并且完全的債務結構網絡比非完全的債務結構網絡在應對外部沖擊時更加富有彈性;而后Allen等（2009）[8]研究發現，當銀行間市場面臨的異質不確定性和總量不確定性無法進行對沖時，整個市場的波動率顯著上升。近年來，學者們認為，銀行間市場的波動性溢出主要通過信用違約和共同資產的持有等兩類渠道進行傳遞，銀行間同業市場網絡的暴露會顯著地增加違約風險和共同資產風險的傳染（Caccioli等，2014;Glasserman和Young，2015;Greenwood等，2015;Babus，2016）[9-12]。Roncoroni等（2019）[13]則進行了進一步總結，將銀行間市場的風險傳染渠道分為直接渠道和間接渠道。直接渠道指的是銀行間的雙邊聯系，如銀行間貸款網絡、互相持有對方有價證券等，當某一家銀行或非銀金融機構發生債務違約時，會使得與之具有直接聯系的金融機構受到沖擊，資產負債表發生惡化;間接渠道指的是銀行面臨共同的潛在風險暴露，主要可以分為資產價格波動和信息溢出效應，由于銀行持有共同的資產，當資產價格發生劇烈波動時，風險會在銀行間迅速傳遞。此外，Roncoroni（2019）[13]還發現信息不對稱會進一步加劇負面消息對銀行間市場造成的沖擊。基于以上分析，本文提出以下假設：

假設1：國際銀行間市場具有金融風險傳染的特征，存在波動性溢出效應。

波動性溢出并不是一成不變的，而是隨著時間的變化呈現出動態的特征。Diebold和Yilamz（2009）[14]通過多元GARCH模型得到美國股票市場、債券市場、外匯市場以及大宗商品市場的條件波動率序列，并運用VAR模型下的方差分解構建波動性溢出矩陣，結果發現金融危機之前各市場間波動性溢出相對平穩，而金融危機爆發期間波動性溢出顯著增強。Mensi等（2018）[15]以MSCI全球股票市場指數作為代理變量，對全球股票市場間的波動性溢出效應進行研究，并采用滾動窗口回歸對該效應進行了動態分析，結果表明，在金融危機期間波動性溢出效應顯著增強，并且美國市場為凈的波動性溢出國，其余經濟體均為風險承受者。楊子暉和周穎剛（2018）[16]采用隱含波動率作為未來市場實際波動的代理變量，借助“有向無環圖技術方法”和網絡拓撲分析方法對全球金融風險溢出的動態演變進行分析，結果發現在金融市場劇烈動蕩時期，全球各個金融市場的波動性溢出效應顯著增強，使得系統性金融風險迅速積聚。趙瓊和郭程翔（2019）[17]利用BEKK-GARCH 模型對英國脫歐前后英鎊與主要貨幣之間的波動性及其溢出效應進行研究，發現英國脫歐前，英鎊與歐元、瑞士法郎以及人民幣之間存在較強的因果關系和相互波動關系;然而在脫歐后，英鎊與人民幣之間不存在格蘭杰因果關系，人民幣與歐元、瑞士法郎之間的波動溢出關系在減弱。新冠肺炎疫情的暴發，吸引了人們對國際金融風險跨境溢出效應的關注，錢東平（2020）[18]運用網絡分析法研究了在新冠肺炎疫情“黑天鵝”事件影響下的國際金融風險傳染特征，結果表明新冠肺炎疫情的暴發使得金融風險的跨市場傳染明顯加劇，同時存在著聚集現象。疫情暴發所引發的波動性溢出具有結構性特征，會從多個渠道對市場的正常運行產生沖擊（吳振宇等，2020）[19]。方意和賈妍妍（2020）[20]對新冠肺炎疫情沖擊下外匯市場的波動性溢出效應進行了研究，發現在疫情期間新興市場國家的波動性溢出明顯上升，并且隨著每日確診病例的增加，風險水平持續攀升。劉精山（2021）[21]運用TVP-VAR-SV模型研究了疫情對我國金融市場的動態沖擊，發現波動性溢出具有明顯的異質性、時變性以及區域聚集性。基于上述分析，本文提出如下假設：

假設2：不同經濟體的波動性溢出程度不同，且呈現出時變、動態的特征。

假設3：金融危機以及新冠肺炎疫情等“黑天鵝”事件的沖擊，會使得波動性溢出程度急劇上升。

三、樣本、數據與實證模型

（一）數據說明

現有文獻主要采用三個月LIBOR-OIS指標作為銀行間市場流動性風險的代理變量。利差增大意味著銀行間普遍缺乏信心、惜貸情緒趨高，銀行間市場流動性緊張。因此，本文選取三個月美元、歐元、英鎊、日元LIBOR-OIS分別作為美國、歐元區、英國以及日本銀行間市場流動性風險的代理變量。由于國內缺乏相應的OIS利率數據，本文參照美國芝加哥商品交易所三個月美元隔夜指數互換期貨設計原理計算人民幣OIS利率，計算公式如下：

[OIS=i=1n（1+di360×ri100）-1×360D×100] （1）

其中，[D]表示參考期內實際天數，[di]表示相鄰兩個交易日之間的間隔天數，[n]表示參考期內實際交易天數。[ri]是用于計算的標的利率，本文選取隔夜SHIBOR作為計算人民幣OIS利率的計算標的，在此基礎上計算三個月SHIBOR-OIS利差，衡量我國銀行間市場流動性風險。

依據數據的可獲得性，本文所選取的樣本區間為2007年3月1日—2020年6月22日，數據來源于彭博數據庫和萬得數據庫。

（二）VARMA-AGARCH模型

以多元GARCH模型為代表的計量方法對研究不同市場間關系提供極大的技術支持。Bollerslev （1990）[22]提出的CCC-GARCH模型可用來分析多個序列間的相關性，設定形式如下：

[yt=E（ytFt-1）+εt]

[εt=Dtηt]? ? ? （2）

[Var（εtFt-1）=Ht=DtΓDt]

其中，[Ft]為到[t]期為止的所有信息集;[ηt=（η1t，…，ηmt）]是標準化殘差序列;[Dt=dingh121t，…，h12mt]

是一個對角陣，對角線上的元素為各個市場擾動項的條件標準差，并隨時間變化而變化;[Γ=ρij]是一個對稱的恒定的條件相關系數矩陣，即[ρij=ρji]，且[ρij>0]。假定[hit]服從GRGARCH（r，s）形式：

[hit=ωi+l=1rαilε2it-1+l=1Sβilhit-1]? （3）

CCC-GARCH模型只考慮各時間序列間相關性，并未分析各序列間波動率的相互作用。VARMA-GARCH模型則設定單一市場的條件波動率，除了與自身市場的前期沖擊和前期波動率相關，也會受到其他市場的前期沖擊以及前期條件波動率的影響。模型設定如下所示：

[Φ（L）（yt-μ）=Ψ（L）εt]

[εt=Dtηt]

[ht=w+l=1rAlεt-1+l=1sBlht-1]

[Φ（L）=Im-Φ1L-…-ΦpLp]，[Ψ（L）=Im-Ψ1L-…-ΨqLq]為滯后算子多項式，[w]是常數向量，[ε=（ε21t，…，ε2mt）]、[ε=（ε21t，…，ε2mt）]、[ht=（h1t，…，hmt）]、[A1（l=1，…，r）]和[B1（l=1，…，s）] 為[m×m]的系數矩陣，分別代表ARCH效應和GARCH效應。波動性溢出效應可通過跨市場擾動項和條件波動率系數來體現，考慮到正負市場沖擊對條件波動率存在非對稱影響， VARMA-AGARCH模型對條件方差方程做出如下改進：

[ht=w+l=1rAlεt-1+l=1rClI（ηt-1）εt-1+l=1sB1ht-1]? （4）

其中，[I（ηt）=diang（I（ηit））] 是一個示性函數，即：

[I（ηit）=1，? if εit<00，? if εit≥0]? ?（5）

[Cl]是[m×m]的系數矩陣，如果回歸結果在統計上顯著，那么正負沖擊對條件波動率存在非對稱特征。

（三）波動性溢出矩陣

為進一步明確國際銀行間市場的相互作用，本文依據Diebold和Yilmaz （2009）[14]提出的網絡拓撲分析方法，在預測誤差方差分解基礎上構建波動性溢出矩陣。Matthias和Gisler （2015）[23]嘗試將協方差加入VAR模型的輸入值，并與只將方差作為輸入值的結果進行對比，發現波動性溢出指數顯著提高，說明考慮各市場對整個銀行間系統的聯合作用至關重要。因此，本文VAR輸入變量為VARMA-AGARCH模型估計的方差和協方差，并基于預測誤差方差分解，構造波動性溢出矩陣（見表1）。

在該溢出矩陣中，第一行變量為波動性溢出的輸出方，第一列表示波動性溢出的吸收方。運用預測誤差方差分解，本文將第[j]個變量的正交化沖擊對第[i]個變量向前H期預測均方誤差的貢獻比例定義為[j]市場對[i]市場的波動性溢出，即：

[Si←j=h=0H-1a2h，ijh=0H-1trace（AhA'h）×100]? （6）

[h=0H-1a2h，ij]表示因市場[j]的沖擊而引發市場[i]波動在預測期為H的誤差方差，[h=0H-1trace（AhA'h）]為H期的總體預測誤差方差。[Si←j]表示由市場[j]的波動沖擊而導致市場[i]變動的比重，[Sj←i]為市場[i]的擾動導致市場[j]變動的比重，因此，可以有效地從兩兩對應的角度衡量市場之間的波動溢出強度。“OUT”所在行元素表示各列非對角線上元素的和，衡量某一市場對其他市場波動性溢出效應;“IN”所在列的元素表示各行非對角線上元素的和，衡量其他市場對某一市場的波動性溢出，即該市場的波動性吸收;兩者相減則可表示某一市場凈波動性溢出效應。在此基礎上，對“OUT”所在行元素或者“IN”所在列元素加總并求平均值，計算波動性溢出指數，有效衡量整個系統波動性溢出效應。

四、實證分析

（一）描述性分析

表2報告了變量的描述性統計特征，其中，美元（US）、歐元（EUR）、英鎊（UK）、日元（JPN）分別為三個月的LIBOR-OIS，人民幣（CHN）為三個月SHIBOR-OIS，單位為基點，即萬分之一。結果顯示，樣本數據的極差和標準差均較大（尤其是中國、英國和美國），說明國際銀行間市場波動劇烈。JB統計量的值顯著異于零，樣本時間序列不服從正態分布的假設，可考慮采用GARCH族模型進行實證分析。

（二）平穩性檢驗和ARCH效應檢驗

由于ADF檢驗和PP檢驗易犯第二類錯誤，檢驗功效相對較低。本文采取KPSS平穩性檢驗，該檢驗原假設為“時間序列平穩”。本文依據序貫t規則確定平穩性檢驗的滯后階數，結果顯示序列非平穩。對所有數據進行一階差分處理之后，都通過了平穩性檢驗。差分后數據存在明顯的波動性聚集現象（見圖1），且在金融危機、歐債危機以及新冠肺炎疫情暴發期間均存在劇烈波動。另外，本文采取ARCH-LM異方差檢驗（見表3），結果顯示存在條件異方差，可采用GARCH族模型進行分析。

（三）國際銀行間市場波動性溢出效應分析

本文采用VARMA-AGARCH模型研究國際銀行間市場的波動性溢出效應，根據AIC和SIC信息準則，將均值方程設置為ARMA（1，1）的形式，ARCH項和GARCH項的滯后階數均設定為1，即對于VARMA-AGARCH模型[p=q=r=s=1]。由于篇幅限制，表4僅列示方差方程估計結果。其中，ARCH項系數和GARCH項系數在統計上是顯著的，說明市場波動率會受到自身市場前期沖擊和條件波動率的影響。我國銀行間市場波動除了受到自身沖擊和前期波動影響，還會受到美國、歐元區、英國以及日本銀行間市場短期和長期波動影響。可見，金融一體化不僅加速了國際資本的跨境流動，而且增強了金融風險的傳染效應。此外，參數[γ]均在1%的水平下顯著，說明負的市場沖擊對市場波動的影響大于正的市場沖擊，即市場沖擊存在非對稱性的特征。在金融市場劇烈動蕩時期，我國與其他國家（地區）銀行間市場的波動性溢出效應顯著增強。

通過VARMA-AGARCH模型證實了美國、歐元區、英國、中國以及日本等銀行間市場存在波動性溢出效應，但對于溢出的方向和溢出的程度無法作出具體判斷。因此，本文參照第三部分提到的方法構建波動性溢出矩陣，用VARMA-AGARCH模型得到的方差和協方差作為VAR輸入值，依據信息準則，VAR滯后長度選為2，預測窗寬定為10天。具體結果如表5所示。

全樣本期間，整個國際銀行間市場波動性溢出總效應為86.30%。在由中國、美國、歐元區、英國以及日本所構成的國際銀行間系統中，美國波動性溢出最大，達到490.90%，對英國和日本的溢出尤為明顯。美元是全球最重要的儲備貨幣，借助美元霸權，美國金融市場對其他經濟體的金融市場有著重大影響。歐元區波動性溢出僅次于美國，高達388.94%。在歐債危機期間LIBOR-OIS利差一度擴大到100bp左右，整個國際銀行間市場流動性空前緊張。英國波動性溢出排在第三位，達到100.89%。近年來，英國脫歐進程的跌宕起伏給全球銀行間市場帶來了極大的不確定性。日本的波動性溢出為45.13%，略高于中國。但是，考慮到協方差序列后，美國和中國共同的波動性溢出達到61.70%，甚至高于美國和歐元區的共同溢出。2010年，我國GDP總量超過日本成為世界第二大經濟體。隨著“一帶一路”倡議的不斷推進以及金融市場擴大開放，中國經濟對全球經濟影響持續擴大。從“NS”列來看，美國、歐元區、英國的凈波動性溢出是正的，說明當前國際銀行間市場的重心仍然在歐美地區。

（四）危機期間波動性溢出效應分析

已有文獻研究發現，在危機期間金融市場的波動性溢出程度明顯高于市場平穩時期，并且本文在VARMA-AGARCH的實證結果中也發現市場沖擊對波動性溢出的影響存在非對稱性，即負的市場沖擊對市場波動的影響大于正的沖擊。因此，本文分別對金融危機期間以及新冠肺炎疫情暴發階段國際銀行間市場的波動性溢出網絡進行分析，并與全樣本結果進行對比①。金融危機區間為 2007年8月9日危機初次顯現到2008年9月15日雷曼兄弟申請破產危機達到高潮，新冠肺炎疫情區間為2020年1月1日至6月22日，具體結果見表6。

金融危機期間，國際銀行間市場波動性溢出總效應高達89.18%，相對于全樣本，該值明顯提高，且美國的波動性溢出達到了830.35%，遠高于全樣本的490.90%，說明市場風險迅速從美國傳導至其他經濟體，使全球銀行間市場陷入低迷。金融危機以美國為中心跨境擴散，對其他經濟體的市場穩定造成強烈沖擊，美國對我國銀行間市場的溢出也上升到33.88%，遠高于全樣本期間的5.54%。因此，在全球市場動蕩時期，中國監管當局應重點注意美國市場異常波動，防止市場風險通過國際銀行間市場傳導至國內。

新冠肺炎疫情的暴發對全球經濟造成了重大影響。在疫情暴發期間，國際銀行間市場波動性溢出指數高達93.92%，明顯高于全樣本的86.30%，甚至超過了金融危機時期。美國的波動性溢出較全樣本期間急劇上升，達到了822.05%，略低于金融危機期間的830.35%。以新冠肺炎疫情為代表的全球性突發公共衛生事件在短期對市場的沖擊不亞于金融危機。我國在疫情期間溢出更是上升到第二位，達到165.58%。如果在對疫情的防控以及政策應對上不夠及時，則有可能進一步惡化市場。金融機構業務不可避免受到沖擊，貸款逾期率和不良率上升以及債券違約事件增加，導致流動性風險和信用違約風險積聚，企業破產風險急劇增高。因此，各國紛紛開始向市場注入“無限流動性”。

波動性溢出效應在金融危機和新冠肺炎疫情時期大幅增強，一方面，是因為突發性的危機事件使得各銀行間市場出現惜貸情緒，造成整個市場流動性的缺失;另一方面，則是因為這類“黑天鵝”事件激發了投資者的恐慌情緒，進一步演化為對資產的拋售，導致其價格暴跌，如疫情期間美股在3月9日、3月12日、3月16日、3月18日短短10天內出現四次熔斷。

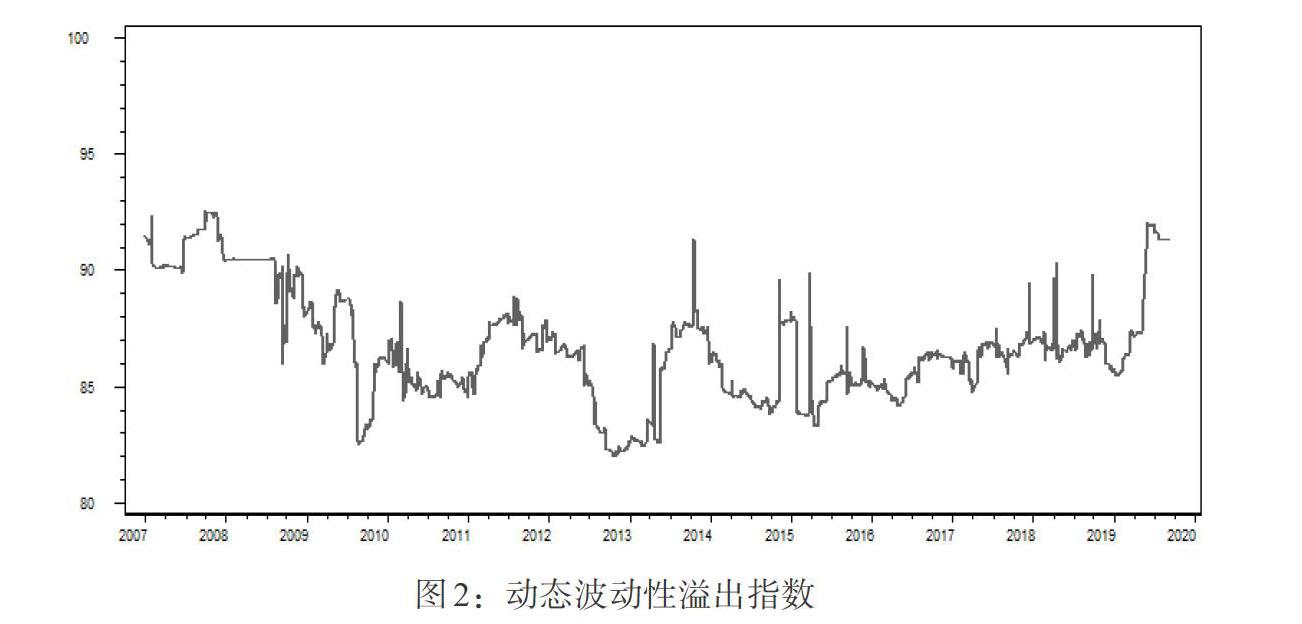
為了分析整個樣本期間波動性溢出效應的動態特征，研究市場危機與波動性溢出程度的關系，本文參考Ribeiro（2017）[6]的研究方法，以200天為滾動窗口，對VAR（2）模型重新進行估計，并依據預測誤差方差分解，計算動態波動性溢出指數（見圖2）。從圖2可以發現，在金融危機期間整個市場的溢出效應顯著增強，且在2008年中期發生劇烈波動，而后隨著各國紛紛采取相應的救市措施，溢出有所下降，但歐債危機爆發后又有所上升。2014—2015年全球股市發生劇烈動蕩，國際銀行間市場也遭受相應沖擊，波動性溢出指數一度超過90%。2019年第二季度至今，市場的波動性溢出指數持續上升，國際銀行間市場風險溢價急劇上漲，波動性溢出效應顯著增強。原因在于，2019年我國與美國的貿易摩擦給全球經濟帶來巨大的不確定性;新冠肺炎疫情使得原本不確定的經濟在短期內遭受劇烈沖擊，全球性危機的征兆初步浮現。

五、結論

隨著中國金融開放的程度不斷提高，銀行間市場與其他經濟體的聯系愈發緊密，本國市場的穩定性易受到國際市場沖擊。由實證結果可知，國際銀行間市場存在顯著的波動性溢出效應，且美國是整個市場中最大的風險輸出方和全球金融風險中心。全球性金融危機和突發公共衛生事件等負面沖擊會使得波動性溢出急劇上升。波動性溢出指數呈現動態特征，在市場風險溢價上升時顯著增強。因此，中國監管當局應強化銀行資產負債管理，提高銀行間市場風險管理水平，實時捕捉美國銀行間市場動態規律，完善國際銀行間市場風險預警機制，有效遏制銀行間市場的跨境傳導，健全金融協調監管機制，及時采取有效措施應對突發公共衛生事件等“黑天鵝”所引起的負面沖擊，防止因金融市場震蕩而產生系統性風險。

注：

①由于篇幅限制，本文僅列示了部分結果。

參考文獻：

[1]劉沖， 盤宇章. 銀行間市場與金融穩定——理論與證據 [J].金融研究，2013，（12）.

[2]Dornbusch R，Park Y C，Classens S. 2000. Contagion：Understanding How It Spreads [J].World Bank Research Observer，15（2）.

[3]Forbes K J，Rigobon R. 2002. No Contagion，Only Independence：Measuring Stock Market Comovements [J].The Journal of Finance，57（5）.

[4]張兵，范致鎮，李心丹.中美股票市場的聯動性研究[J].經濟研究，2010，45（11）.

[5]Balli F，Hajhoj H R，Basher S A，Ghassan H B. 2015. An Analysis of Returns and Volatility Spillovers and Their Determinants in Emerging Asian and Middle Eastern Countries [J].International Review of Economics and Finance，39（2）.

[6]Ribeiro P P，Curto D C. 2017. Volatility Spillover Effects in Interbank Money Markets [J].Review of World Economics，153（9）.

[7]Allen F，Gale D. 2000. Financial Contagion [J].The Journal of Political Economy，108（1）.

[8]Allen F，Carletti E，Gale D. 2009. Interbank Market Liquidity and Central Bank Intervention [J].Journal of Monetary Economics， 56（1）.

[9]Caccioli F，Shrestha M，Moore C，Farmer J D. 2014. Stability Analysis of Financial Contagion due to Overlapping Portfolios [J].Journal of Banking & Finance，46（3）.

[10]Glassrman P，Young H P. 2015. How Likely is Contagion in Financial Networks？ [J].Journal of Baking & Finance，50（1）.

[11]Greenwood R，Landier A，Thesmar A. 2015. Vulnerable Banks [J].Journal of Financial Economics，115（3）.

[12]Babus A. 2016. The Formation of Financial Networks [J].The Rand Journal of Economics，47（2）.

[13]Roncoroni A，Battiston S，D'Errico M，et al. 2019. Interconnected Banks and Systemically Important Exposures[R].ECB Working Paper，No. 2331.

[14]Diebold F X，Yilmaz K. 2009. Measuring Financial Asset Return and Volatility Spillovers，with Application to Global Equity Markets [J].Economic Journal，119（2）.

[15]Mensi W，Boubaker F Z，Al-Yahyaee K H，Kang S H. 2018. Dynamic Volatility Spillovers and Connectedness Between Global，Regional，and GIPSI Stock Markets [J].Finance Research Letters，25（3）.

[16]楊子暉，周穎剛.全球系統性金融風險溢出與外部沖擊 [J].中國社會科學，2018，（12）.

[17]趙瓊，郭程翔.英國脫歐前后英鎊與主要貨幣之間的波動性及其溢出效應研究 [J].經濟問題，2019，（11）.

[18]錢東平.新冠肺炎疫情加劇了國際金融風險傳染嗎？ [J].當代金融研究，2020，（5）.

[19]吳振宇，朱鴻鳴，朱俊生.新冠肺炎疫情對金融運行的影響及政策建議 [J].經濟縱橫，2020，（3）.

[20]方意，賈妍妍.新冠肺炎疫情沖擊下全球外匯市場風險傳染與中國金融風險防控 [J].當代經濟科學，2021，（1）.

[21]劉精山.新冠肺炎疫情沖擊背景下金融風險的傳導與防范研究——基于金融壓力視角的實證分析 [J].華北金融，2021，（1）.

[22]Bollerslev T. 1990. Modelling the Coherence in Short-run Nominal Exchange Rate：A Multivariate Generalized ARCH Approach [J].Review of Economics and Statistics，72（3）.

[23]Matthias R F，Gilser I M. 2015. A Variance Spillover Analysis Without Covariances：What do We Miss？ [J]. Journal of International Money and Finance，51（3）.

Research on the Volatility Spillover Effects Among the International Interbank Market from the Perspective of Network

Song Qin/Fang Wen/Gan Ke

（School of Economics and Business Administration，Central China Normal University，Wuhan? ?430079，Hubei，China）

Abstract：This paper selects the three-month LIBOR-OIS and SHIBOR-OIS data of USD，EUR，GBP，JPY and RMB from March 2007 to June 2020，and uses the VARMA-AGARCH model and network topology analysis to study the volatility spillover effects in the interbank markets of US，Eurozone，UK，China and Japan. And the volatility spillover indices are also constructed. It is found that： there are significant volatility spillover effects in the international interbank market，where conditional volatility is affected not only by prior shocks and volatility in its own market，but also by disturbances of other markets;volatility spillover effects in international interbank markets increased significantly during both the financial crisis and the outbreak of COVID-19，showing dynamic characteristics; the volatility spillover from the U.S. to the interbank market in other economies is the largest and rises sharply in times of crisis，so China's interbank market supervision should guard against cross-regional transmission of foreign market risks，especially the imported shocks from U.S. market volatility.

Key Words：international interbank market，VARMA-AGARCH model，volatility spillover matrix