高中數(shù)學(xué)三角函數(shù)最值問(wèn)題分析

楊克林

(福建省漳浦第一中學(xué) 363200)

三角函數(shù)習(xí)題類(lèi)型靈活多變，解題的思路也有所不同.其中運(yùn)用三角函數(shù)性質(zhì)、運(yùn)用輔助角、運(yùn)用均值不等式以及換元法是解題中較為常用的方法.教師授課中為使學(xué)生掌握不同方法的具體應(yīng)用，使其更好地把握解題中的相關(guān)細(xì)節(jié)，應(yīng)注重為學(xué)生做好解題示范.

一、運(yùn)用三角函數(shù)性質(zhì)求最值

運(yùn)用三角函數(shù)性質(zhì)求最值的思路為：其一，靈活運(yùn)用相關(guān)的誘導(dǎo)公式等將函數(shù)表達(dá)式整理成y=Asin(ωx+φ)+h(或y=Acos(ωx+φ)+h)的形式；其二，根據(jù)已知條件找到ωx+φ的取值范圍；其三，聯(lián)想所學(xué)的三角函數(shù)單調(diào)性知識(shí)，在給定的定義域中求出最值.

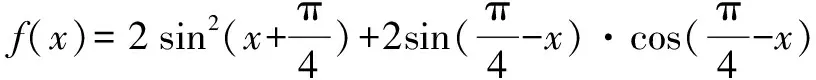
題目給出的函數(shù)f(x)的表達(dá)式較為復(fù)雜，解答該題時(shí)的第一印象便是先使用誘導(dǎo)公式、兩角和差公式、降冪公式、輔助角公式等將函數(shù)f(x)的表達(dá)式化簡(jiǎn)成類(lèi)似“y=Asin(ωx+φ)+h”的形式.而后根據(jù)給出的定義域區(qū)間，采用整體思想結(jié)合三角函數(shù)圖象，分析其在對(duì)應(yīng)區(qū)間上的單調(diào)性，求出函數(shù)最小值即可.

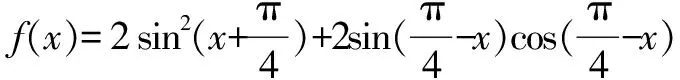
=sin2x+cos2x+1

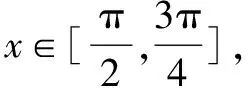
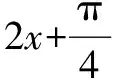
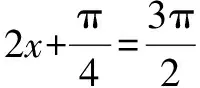
二、運(yùn)用輔助角求最值

運(yùn)用輔助角求最值應(yīng)牢記輔助角構(gòu)造公式，尤其應(yīng)明確引入的角度與條件之間的內(nèi)在關(guān)聯(lián)，通過(guò)運(yùn)用已知條件求解出未知參數(shù)，而后運(yùn)用三角函數(shù)的邊界性確定最終結(jié)果.

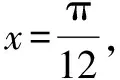
題目中函數(shù)f(x)的表達(dá)式并不復(fù)雜.根據(jù)經(jīng)驗(yàn)，需要引入輔助角θ進(jìn)行化簡(jiǎn)，化陌生為熟悉.同時(shí)，結(jié)合已知條件中函數(shù)對(duì)稱(chēng)軸以及三角函數(shù)圖象特點(diǎn)，確定對(duì)稱(chēng)軸的表達(dá)式，而后將已知條件代入，計(jì)算出ω的值.最后利用輔助角之間的關(guān)系，求出a的值，問(wèn)題便可迎刃而解.

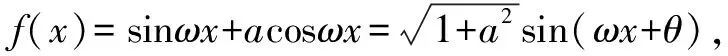
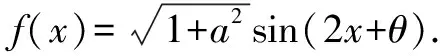
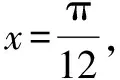
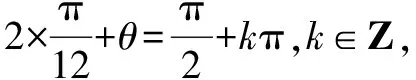
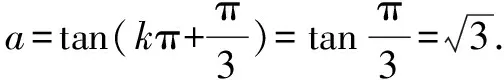
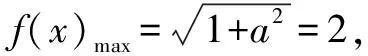
三、運(yùn)用均值不等式求最值

均值不等式常用于求解三角函數(shù)最值.為保證解題結(jié)果的正確性，運(yùn)用均值不等式時(shí)應(yīng)注意把握參數(shù)的取值范圍，牢記均值不等式成立的條件，尤其針對(duì)無(wú)法使用均值不等式的習(xí)題， 應(yīng)注重結(jié)合已知條件對(duì)相關(guān)的角度進(jìn)行拆分，湊成能夠運(yùn)用均值不等式的形式.當(dāng)然等號(hào)成立的條件應(yīng)保證參數(shù)能夠取到.

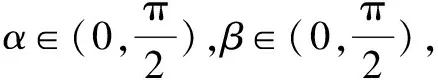
習(xí)題題干簡(jiǎn)潔，認(rèn)真分析已知條件以及要求解的問(wèn)題，可知需要對(duì)角進(jìn)行合理的拆分，以便更好地借助兩角和與差的三角函數(shù)知識(shí)進(jìn)行化簡(jiǎn).同時(shí)，積極聯(lián)系所學(xué)，巧妙地運(yùn)用兩個(gè)角度的值配湊出對(duì)應(yīng)的均值不等式，求出cosβ的最小值，尤其要注重分析均值不等式等號(hào)成立的條件，保證推理的嚴(yán)謹(jǐn)性.

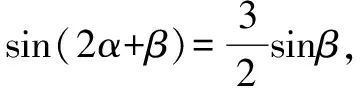
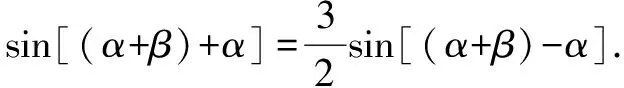
所以sin(α+β)cosα+cos(α+β)sinα

整理,得sin(α+β)cosα=5cos(α+β)sinα.

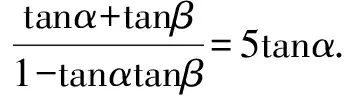
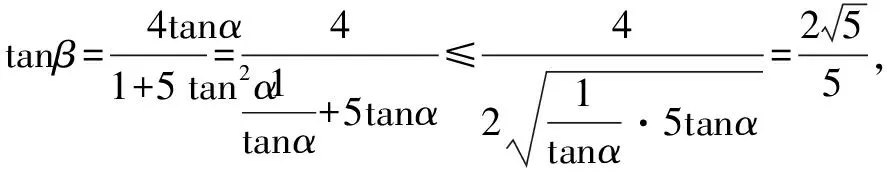
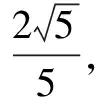
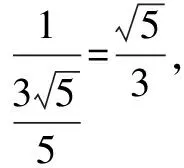
四、運(yùn)用換元法求最值

運(yùn)用換元法求解三角函數(shù)最值具有一定的技巧，求解時(shí)需要先對(duì)已知條件進(jìn)行轉(zhuǎn)化，而后進(jìn)行合理地?fù)Q元.當(dāng)然換元前后參數(shù)的取值范圍不能發(fā)生變化.而后聯(lián)系所學(xué)的函數(shù)知識(shí)求出最值.

例4已知A,B,C為銳角ΔABC的三個(gè)內(nèi)角，且滿(mǎn)足tanB+tanC=2tanBtanC，則tanAtanBtanC的最小值為( ).

A.2 B.4 C.6 D.8

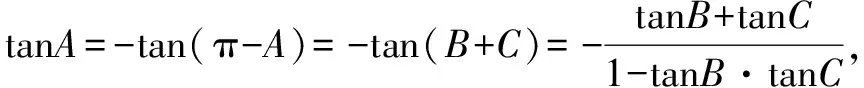
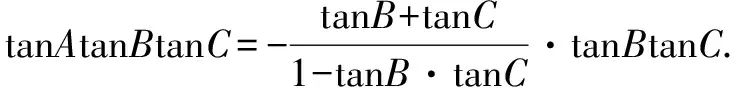
又因?yàn)閠anB+tanC=2tanBtanC，

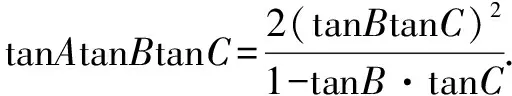
令t=tanBtanC，因?yàn)锳,B,C均為銳角，因此tanA>0，tanB>0，tanC>0.

所以1-tanBtanC<0，則t>1.

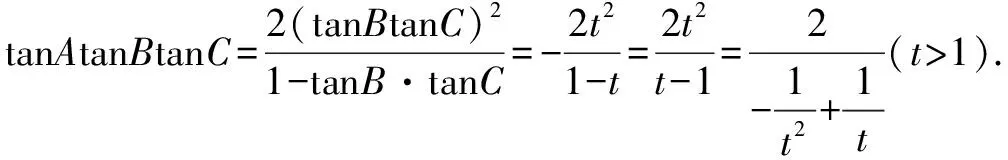
故tanAtanBtanC≥8，其最小值為8，此時(shí)t=2，故選D.

三角函數(shù)最值問(wèn)題在高考中的出現(xiàn)頻率較高，考查的知識(shí)點(diǎn)較多，解題思路靈活多變.解題時(shí)只有找到正確的思路，才能高效地加以解答，因此教師授課中為提高學(xué)生解答三角函數(shù)最值問(wèn)題的能力，應(yīng)結(jié)合自身教學(xué)經(jīng)驗(yàn)，為學(xué)生講解經(jīng)典習(xí)題，并與學(xué)生一起分析解題思路，展示具體的解題過(guò)程，在學(xué)生頭腦中留下深刻印象.同時(shí)課堂上注重預(yù)留一定的空白，鼓勵(lì)學(xué)生做好聽(tīng)課總結(jié)，對(duì)相關(guān)題型分門(mén)別類(lèi)，認(rèn)真分析相關(guān)的解題思路，在平時(shí)的訓(xùn)練中加以靈活運(yùn)用，實(shí)現(xiàn)解題能力更好的提升.