一道數列證明題的解題微探

朱衛中 吳 凱

(浙江省湖州市菱湖中學 313018)

一、原題再現

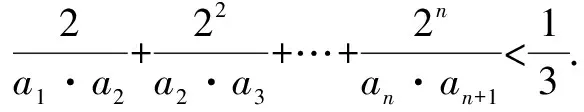
二、典型錯解分析

以上兩個錯解已經初步具備了放縮思想，但還未能達到題目的要求，那么，如何處理才能實現正確的解答，一起來看下面四個角度的思考.

三、四個角度的解法探究

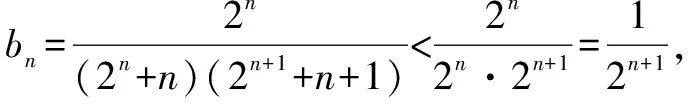
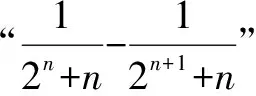
點評注意考慮分子特征形成放縮.

點評本解法采用了“化繁為簡”的策略，過程更加清楚簡便，放縮恰到好處，在處理“裂項”時也需注意“同構”的問題.

四、教學感悟

《普通高中數學課程標準(2017年版2020年修訂)》明確指出：“高中數學教學以發展學生數學學科核心素養為導向，啟發學生思考，引導學生把握數學內容的本質，凸顯數學的內在邏輯和思想方法.”因此，在數列的解題教學中，教師可關注以下三點：

首先，放縮問題是近幾年高考的常考題，將數列求和、不等式證明有機融合，這類考題能充分檢測考生的數學核心素養，有效鑒別考生的解題能力，它是受命題者青睞的題型之一，因此，數列放縮證明問題是高考備考復習的重點內容，在教學中需要增加教學課時，重視解題訓練.