高中數學解題中分類討論思想的有效應用

翟陽琴

(江蘇省南通市海門第一中學 226100)

基于數學視角來看，有些問題結論不是唯一確定的，或者在解題中不能以統一的形式來研究，或者部分已知量是字母形式，字母取值不同所得結果也不同.這時應根據題目的特點和要求分成若干類，轉化成若干個小問題來解決，即為分類討論思想的應用.在高中數學解題教學中，教師需依據題目情況指引學生有效應用分類討論思想，提高他們的解題效率.

一、分類討論思想有效應用于集合解題

集合作為高中數學教學中的入門級內容，也是高中生最先接觸的數學知識，雖然學習起來難度不是特別大，運算過程也不是過于繁瑣，不過在平常考試與高考中都屬于必考類題型，占據著一定的分值比例，解決好集合類的題目能顯著增強他們學習數學的自信.在高中數學集合解題教學中，教師需引領學生對集合與集合及集合與元素間的關系作分類處理，部分集合問題則存在參數，他們均需準確分類后計算，從而得出正確答案，以免遺漏或多余.

例1同時滿足(1)集合M?{1，2，3，4，5}；(2)如果a∈M，則(6-a)∈M的非空集合M有多少個？且寫出這些集合.

解析本道題需按照集合M中元素個數進行分類討論，①當M中只有1個元素時，如果3∈M，則6-a=6-3=3∈M，所以M={3}；②當M中有2個元素時，滿足條件的M有2個，分別為M={1，5}，M={2，4}；③當M中有3個元素時，滿足條件的M有2個，即為M={1，3，5}，M={2，3，4}；④當M中有4個元素時，滿足條件的M只有1個，M={1，2，4，5}；⑤當M中有5個元素時，滿足條件的M也只有1個，M={1，2，3，4，5}，綜合起來適合條件的集合M一共有7個.

隨后教師可設計一些同類題目展開變式訓練，讓學生繼續運用分類討論思想解題.

該題結合集合運算主要考查分類討論思想的應用，學生需把握好分類的依據是集合的性質，即無序性、互異性與確定性，他們無需計算，只需確保思維完整即可.

二、分類討論思想有效應用于函數解題

函數不僅是高中數學知識體系中的重點，也是難點與常考點，屬于數學考試中常見的一類題目，也是學生感到異常頭疼的數學問題，他們在解題中經常出現錯誤，難以準確把握各種情況，容易導致答案不完整，或范圍過大.因此，在高中數學函數解題教學中，教師需指導學生科學合理地應用分類討論思想，使其認真閱讀題干信息，觀察是否存在變量或特殊要求，根據實際情況展開分類討論.

例2已知函數f(x)=cos2x+asinx-a2+2a+5，有最大值2，求實數a的的值.

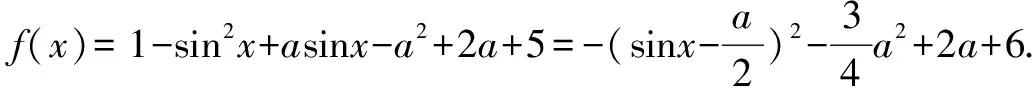
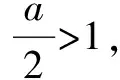
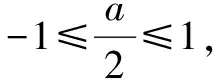
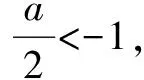
上述案例，教師指導學生應用分類討論思想解答函數類題目時，不僅需對函數自身進行分類，還要討論相應的參數，使其順利找到題目的本質，提升正確率的同時加快解題速度.

三、分類討論思想有效應用于幾何解題

在整個高中數學知識體系中，幾何也占據著較為重要的地位，雖然學生對平面幾何有所了解，但是高中階段以研究立體幾何為主，涉及到的知識點還較多，相應的題目難度系數也更高，他們很難順暢解題.高中數學教師在立體幾何解題教學中，可以引導學生有效應用分類討論思想，先依據題干信息確定題目類型，再根據關鍵信息展開深入分析，探討每一種可能性的存在，最后逐個列舉出來，以免遺漏掉任何一種情況，從而讓他們得出完整答案.

例3已知線段AB和平面α平行，平面α的斜線A1A，B1B和平面α所對的角分別是30°與60°，且∠A1AB=∠B1BA=90°，AB=a，A1B1=b(b>a)，求線段AB和平面α的距離.

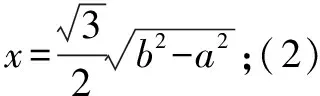
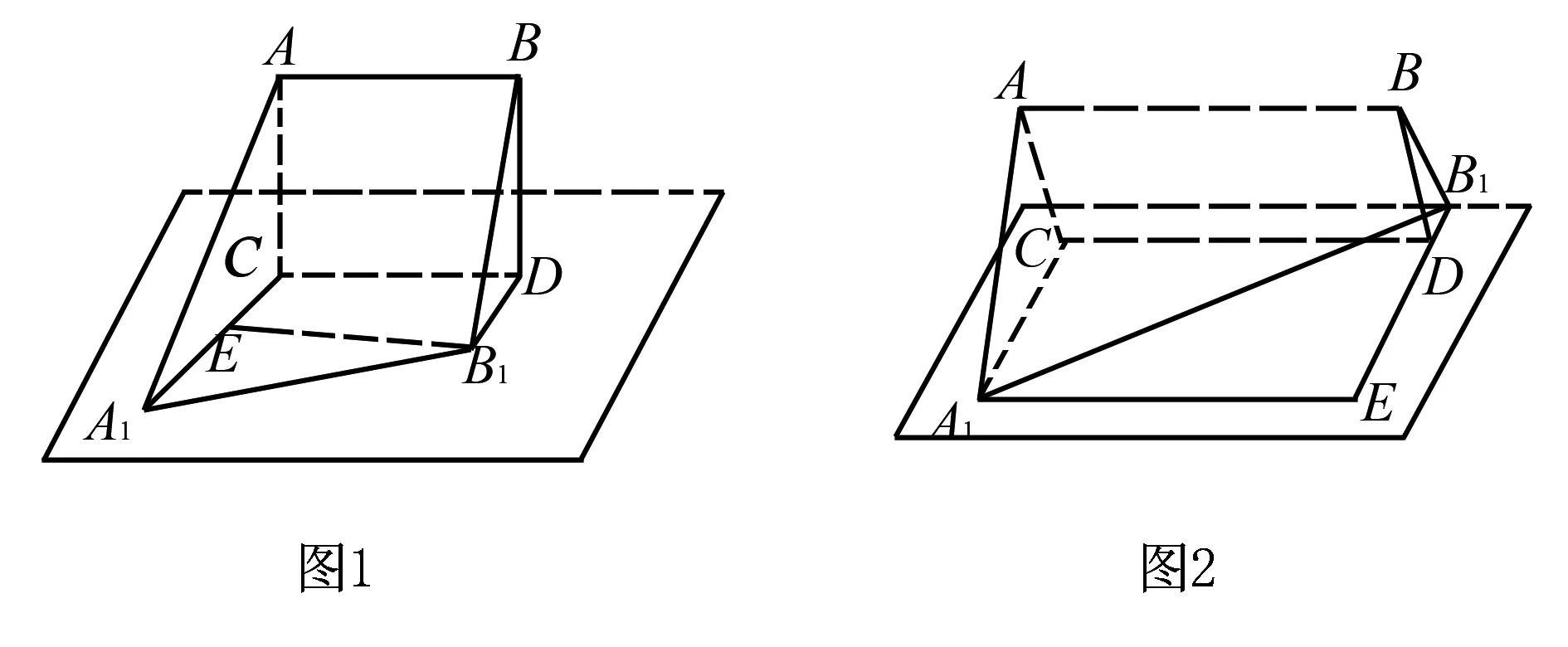
針對上述案例，在解決立體幾何類的題目中，點、線、面是組成幾何圖形的三個基本要素，當這三者的位置關系不確定時，就要對每種情況進行分類討論求解，防止漏解.

四、分類討論思想有效應用于數列解題

高中數學教學中涉及到的數列都是有一定規律的數列，即為等差數列和等比數列，數列類的題目雖然難度一般，但是通常涉及到變量和未知量，要想解決數列難題，分類討論思想同樣適用.在高中數學數列解題教學中，應用分類討論思想可解決數量關系、周期性等問題，具有降低題目難度系數的效果，當學生處理數列問題時，教師應當指引他們有效應用分類討論思想，結合題干信息仔細分類與討論，由此簡化解題過程，使其提高解題速度.

例4已知數列1，2x，3x2，4x3…，求它的前n項和.

解析由于題目中沒有明確指出該數列的類型，所以教師應當提醒學生分類討論，提醒他們考慮到x=0這一特殊情況.

先設Sn=1+2x+3x2+4x3…+nxn-1，再分類討論:

(1)當x=0時，a1=1，a2=2x=0，a3=3x2=0，…，an=nxn-1=0，所以Sn=1+0+0+…+0=1；

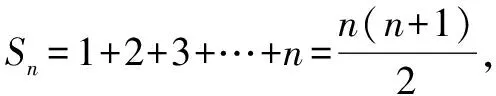
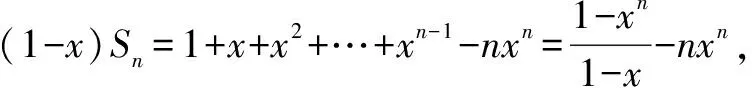
綜合起來，通過對x三種情況的分類討論，最終得到完整的答案.

在上述案例中，當遇到數列問題中存在不確定因素時，教師就要指導學生打破固有思維定勢開放性地思考，盡可能考慮到更多、更全的方面，借此培養他們嚴謹的數學解題思維.

在高中數學解題教學中，分類討論思想有著相當重要的作用，教師需把握好機會，實時將分類討論思想融入到解題教學中，幫助學生在解題中形成良好的分類討論意識，使其有效應用分類討論思想解題，進而提高他們的解題準確度.