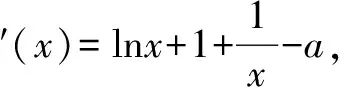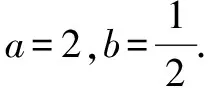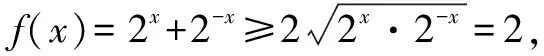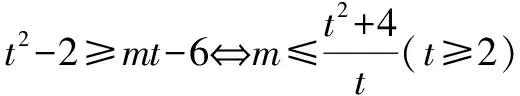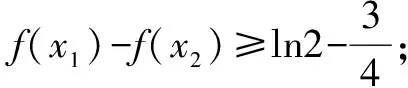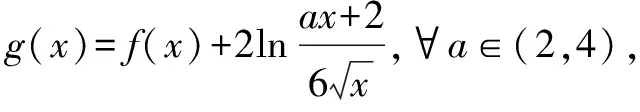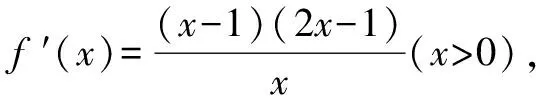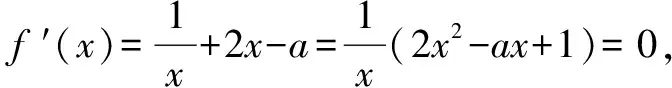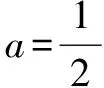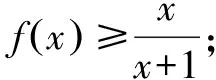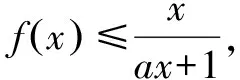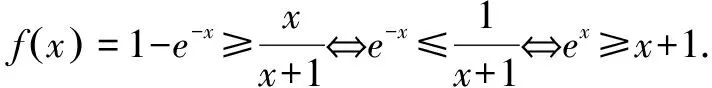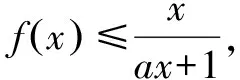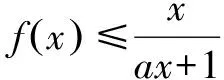一類恒成立問題的一個必要條件及其應用

2021-08-19 05:22:20高群安

數理化解題研究 2021年13期

關鍵詞：解題利用

高群安

(湖北省襄州一中 441104)

定理1設f(x)是定義域內的可導函數，則f(x)≥f(a)在區間[a,b)恒成立的必要條件是f′(a)≥0；f(x)≤f(a)在區間[a,b)恒成立的必要條件是f′(a)≤0.

證明(用反證法)f(x)是可導函數，則f(x)≥f(a)在區間[a,b)恒成立?f′(a)≥0，否則,若f′(x)<0，由連續函數的性質,必存在區間[a，m](m

定理2設f(x)是可導函數，則f(x)≥f(b)在區間(a,b]恒成立的必要條件是f′(b)≤0；f(x)≤f(b)在區間(a,b]恒成立的必要條件是f′(b)≥0.

定理3設f(x)是定義域內的可導函數，f(a)=f′(a)=0,則f(x)≥0在區間[a,b)恒成立的必要條件是f″(a)≥0.

上述定理還可以進一步推廣，運用上述定理解決相關數學問題可以縮小目標范圍，優化解題過程，精簡解答程序，提高解題效率！

例1(2016年高考全國Ⅱ卷·文科20題)已知函數f(x)=(x+1)lnx-a(x-1).

(1)當a=4時，求曲線y=f(x)在(1,f(1))處的切線方程；

(2)若當x∈(1,+∞)時，f(x)>0,求a的取值范圍.

解析(1)易求得曲線y=f(x)在(1,f(1))處的切線方程是y=-2x+2.

點評運用定理，求得參數范圍，再做充分性驗證，簡化了求解過程！

例2(江蘇高考題) 已知函數f(x)=ax+bx(a>0,b>0,a≠1,b≠1).

(2)若01，函數g(x)=f(x)-2有且只有1個零點，求ab的值.

(2)若01，則由f(0)=2，得g(0)=0.當x→-∞時，g(x)→+∞;當x→+∞時，g(x)→+∞.

因為函數g(x)=f(x)-2有且只有1個零點0，所以當x∈(0,+∞)時，g(x)>0?g′(0)≥0;當x∈(-∞,0)時，g(x)>0?g′(0)≤0.故g′(0)=lna+lnb=0?ab=1.

點評解答的第二問，利用極限思想勾畫出了函數g(x)圖象的大致框架.通過數形結合，并利用定理導出g′(0)=0是解答的精妙之筆！當然也可以由可導函數在極值點處的導數為0得g′(0)=0.

例3(2017春·南開區校級月考)已知函數f(x)=lnx+x2-ax(a∈R).

(1)a=3時，求f(x)的單調區間；

本解答通過運算、轉化，巧妙運用本節定理求出了參數范圍.

圖1

例4(2017年高考題)已知函數f(x)=x3+3ax2+3x+1.

(2)若x∈[2,+∞)時，f(x)≥0，求a的取值范圍.

圖2

(1)設a>0,討論y=f(x)的單調性;

(2)若對任意的x∈(0,1),恒有f(x)>1,求a的取值范圍.

(2) 因為f(0)=1, 所以對任意的x∈(0,1),恒有f(x)>1的必要條件是f′(0)=2-a≥0，即a≤2;反之，當x∈(0,1),a≤2時，由(1)知，當0≤a≤2時,f′(x)>0;當a<0時，拋物線g(x)=ax2+2-a的開口向下，g(0)=2-a≥0,g(1)=2,所以x∈(0,1)時，f′(x)>0，所以f(x)在(0,1)上單調遞增, 對任意的x∈(0,1),恒有f(x)>1.所以對任意的x∈(0,1),恒有f(x)>1的a的取值范圍是(-∞,2].

點評解答第(1)問時，注意到了定義域對單調區間的限制；第(2)問，先由必要條件求出a≤2,再利用(1)證明a≤2時，不等式恒成立，簡化了運算過程.

例6 (全國高考題)設函數f(x)=(x+1)ln(x+1).若對所有的x≥0,都有f(x)≥ax成立，求實數a的取值范圍.

解析由題設對所有的x≥0,都有f(x)≥ax?g(x)=(x+1)ln(x+1)-ax≥0恒成立,而g(0)=0,g′(x)=ln(x+1)+1-a, 由本節定理知：g(x)≥0恒成立的必要條件是g′(0)=1-a≥0，即a≤1;反之，當a≤1，x>0時，g′(x)>0,所以g(x)在[0,+∞)單調遞增，所以g(x)≥0，即f(x)≥ax恒成立.

綜上，實數a的取值范圍是(-∞,1].

點評本解答通過構造函數，運用定理，迅速求得參數范圍.

圖3

例7 (2010年新課標全國卷·理21)設函數f(x)=ex-1-x-ax2.

(1)若a=0,求f(x)的單調區間;

(2)若當x≥0時，f(x)≥0，求a的取值范圍.

解析(1)當a=0時，f(x)=ex-1-x,f′(x)=ex-1.如圖3,可知f(x)在(-∞,0)上單調遞減，在(0,+∞)上單調遞增.

點評本解答利用了定理3不等式恒成立的必要條件，求出a的范圍，再作充分性檢驗，優化了解答程序，提高了解題效率.

圖4

例8(2010年大綱全國卷·文21)設函數f(x)=x(ex-1)-ax2.

(2)若當x≥0時，f(x)≥0，求a的取值范圍.

f′(x)的符號如圖4,f(x)在(-∞,-1)，(0,+∞)上單調遞增，在(-1，0)上單調遞減.

(2)因為f(x)=x(ex-1-ax)，所以“當x≥0時,f(x)≥0”?“當x≥0時，g(x)=ex-1-ax≥0”.因為g(0)=0，g′(x)=ex-a，所以當x≥0時，g(x)=ex-1-ax≥0恒成立的必要條件是g′(0)=1-a≥0，即a≤1;反之，當a≤1時，g′(x)≥0，得g(x)在[0,+∞)上單調遞增，所以g(x)≥g(0)=0.

綜上，當x≥0時，f(x)≥0恒成立的a的取值范圍是(-∞,1].

點評本問題(1)利用導函數的圖象直觀，是判斷函數單調性的快捷方法；問題(2)經過等價轉化，再利用本節定理，簡化了解答程序.