速記巧用三角函數誘導公式

宋朝暉

(新疆喀什第六中學 844000)

高一數學《三角函數》一章，學生感覺內容龐雜，知識點眾多，知識間關系錯綜復雜，難以掌握.還有一個大難題：公式多.學生準確記憶、正確運用有一定的難度.問題最典型的是三角函數誘導公式這一節，很多教師在教授時，都要求學生先背公式，再強行套用公式，勉強完成計算.從心理學角度來說，當一個知識沒有被學習者完全理解，對它的記憶是不穩定的.因為不理解，一方面會在使用過程中過于拘謹，表現出僵化教條；另一方面隨著學習的推進、新知識的不斷涌現，會出現記憶偏差，使得計算錯誤不斷.死記硬背的辛苦，記憶不準確，導致解題失敗，消減了學生學習數學的興趣，打擊了學生的自信心.因此，如何讓學生脫離記憶公式的痛苦，輕松快速地記住，并靈活應用誘導公式，就成為了一線教師的一項課題.

一、透徹理解誘導公式的推導過程

新課標下，三角函數概念是在單位圓中定義的.為此，誘導公式的推導，是借助單位圓，利用“角的終邊的對稱關系”來進行的.初學時，經歷直觀形象的推導過程有助于學生理解記憶公式.如圖1，角α終邊交單位圓于點P(x,y)，由對稱關系知，角 2kπ+α，π-α，π+α，-α的終邊與單位圓交點為P1(x,y),P2(-x,y),P3(-x,-y),P4(x,-y).

進而，由任意角三角函數定義可得4組公式：

記憶口訣：函數名不變，符號看象限.

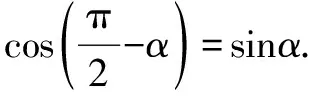
記憶口訣：函數名稱變，符號看象限.

只要理解到位，結合這兩個坐標圖去記憶誘導公式組，不失是一種快捷方法.

二、記憶方法對比

1.口訣記憶法

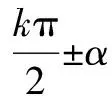
口訣說起來簡單，但學生在應用時，還是常常有人不知所措，不會用.調查發現，是學生不明白口訣的真正含義所致.于是將公式直觀化，列在坐標系中，演變出如下記憶法.

2.圖象記憶法

在圖2,3中，能夠直觀地看到各形式的角應處的象限，確定符號很方便，很準確.學生有了這個圖，誘導公式計算化簡問題的準確率大大地提高了.

三、巧用誘導公式快速計算

簡單的誘導公式計算題學生都能夠看著圖計算正確，但遇到復雜些、綜合性強的計算，學生還會敗下陣來.如教材上的這道題：

例1 化簡

即使是熟記口訣,熟悉圖象的學生，也往往顧此失彼、錯誤不斷.究其原因，如何準確看待這些角，以及化簡時使用誘導公式的先后順序，都影響著結果.

教材上思路是“負化正，正化銳”，把每個因式先統一成誘導公式中的某一形式，再套用誘導公式往下計算.如sin(-π-α)=sin[-(π+α)]=-sin(π+α)=sinα.這種做法，連續多次使用誘導公式，中間環節多，自然增加了學生計算的失誤率.

遇到這類題，我教學生這樣處理：如圖5，先畫一個直角坐標系，再把特殊的軸線角標記在對應軸線上，并記住在x軸上則“名不變，符號看象限”，在y軸上則“名稱變，符號看象限”.這樣原本要多次用誘導公式化簡的，只需用一次即完成，大大縮減中間環節.

sin(3π-α)=sinα;sin(-π-α)=sinα;

于是依靠坐標軸，一步就到位.

此法使學生既快又準地得出結果，體驗到解題的樂趣.這樣對誘導公式進行靈活拓展處理，每一個式子都可以直接用誘導公式口訣化簡，大大減輕了計算量，提高了準確率.

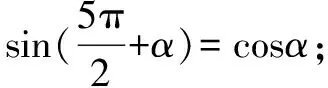
sin(α-2π)=sin(-2π+α)=sinα;

cos(2π-α)=cosα.

于是可以口算，原式=sin2α.

再看兩個模考或高考例子：

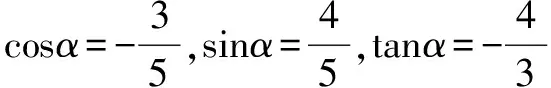
此題后面部分的化簡避不開誘導公式的使用，掌握了巧記方法，則可輕松完成.

分析由題意知，函數y=ax+1+2的圖象過定點A(-1,3),則tanα=-3.

誘導公式在三角函數有關計算中應用廣泛.苦于對繁多的誘導公式記憶不準，學生解三角函數題，難以圓滿.巧妙利用畫坐標系來記憶公式組，既準確，又方便，還快捷.相比機械的“口訣記憶法”，圖象法記憶形象直觀，經歷的中間過程更少、失誤率更低.其中也體現了數形結合、等價轉化等重要思想的應用.