一道自主招生試題的解法探究與變式

賀鳳梅

(新疆伊犁鞏留縣高級中學 835400)

近期，在高三復習課過程中,筆者多次見到與2017年清華大學能力測試第12題同類型的試題，呈現形式多以選擇題或填空題為主.我嘗試著用此題訓練所教的學生，效果極不理想，很多同學幾乎沒有任何頭緒.這種現象引起了筆者的關注，并由此展開了對此題解法的探究，以期達到拋磚引玉的效果.

一、題目呈現

題目(2017年清華大學能力測試第12題)已知實數x,y滿足5x2-y2-4xy=5，則2x2+y2的最小值為( ).

二、總體分析

這道題條件看似簡單，在二元二次的條件下求二次目標函數的最值，但從學生實際解答來看，想要得出正確的結果并不容易.很多同學由于不得要領，一頭霧水，不知從何處著手解答此題.事實上,此題解答的方法有很多種.例如采用配方法，借助三角換元來解決，這是最常規的方法；仔細分析此題，發現等式的左邊可以進行因式分解，而且可以分解成兩個一次因式的積的形式，也可以以此作為解題的突破口；對于這類題，判別式法也是一個常見方法.下面我們從不同的視角來探究此題.

三、解法探究

視角1 依托配方法和三角換元作答.

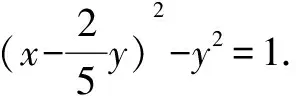
整理,得(25z+33)t2+40t+50-25z=0.

評注通過以上求解過程不難看出，運算過程相當繁瑣，計算量大.分析此題發現，將已知條件左邊進行配方可得平方差關系，這種形式對于一般學生，三角換元不易實現(超出了課程標準，本質是不作要求的同角三角函數平方關系)，而且計算過程相當繁瑣.因此，我們需要另辟蹊徑，以期達到簡便運算，快速正確求解的效果.

視角2 通過普通換元，借助基本不等式作答.

解法2 將5x2-y2-4xy=5的左邊進行因式分解，得(5x+y)(x-y)=5.

設5x+y=a,x-y=b,則有ab=5(a≠0,b≠0).

①

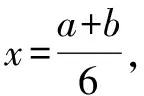
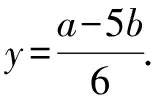
將①②③代入2x2+y2中，

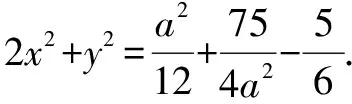
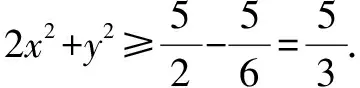
評注解法2通過因式分解后換元，將整理好的式子代入目標函數，消元得到關于a的分式函數，借助于均值不等式得出結果，本解法消元很巧妙.

針對解法2中a,b的關系，可以進一步作消元處理：

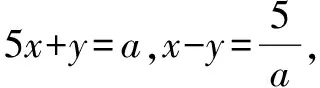
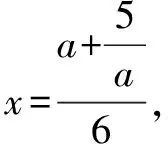
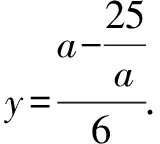
將④⑤代入2x2+y2中，化簡整理，得

下同解法2.

視角3 利用導數作答.

解法4 結合解法2，化簡整理,得

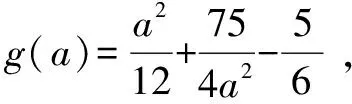
由g′(a)=0，解得a2=15.

當a2∈(0,15)時，g′(a)<0 ,

當a2∈(15,+∞)時，g′(a)>0 ,

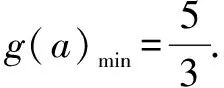
評注利用導數求函數的最值問題是非常實用和重要的方法.大家在平常的教學中，遇到求最值的問題，不妨利用導數求解試試看，一般都能得解.充分展現導數求解最值問題的魅力.

視角4 利用三角換元，借助基本不等式作答.

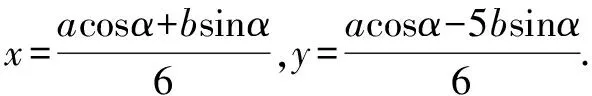
代入2x2+y2，整理并求解,得

由基本不等式,得

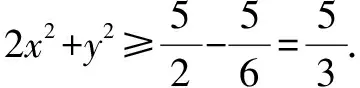
評注本解法中定值absinαcosα=5，提示我們向基本不等式方向尋找突破口，這是一種解題能力.

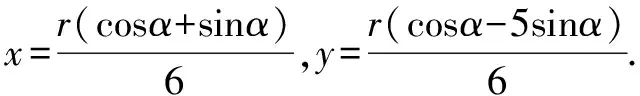
代入2x2+y2中，整理并求解,得

下同解法5.

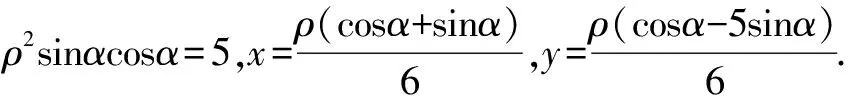
下同解法5.

評注解法5,6,7本質上是相通的，我們期望這些訓練讓學生的知識融會貫通，在比較中發現知識間的聯系.

視角5 巧用三角換元，借助輔助角公式作答.

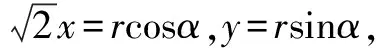
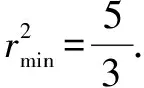
評注輔助角公式在三角函數求最值時也經常出現，當然更多的時候是以配湊特殊的角的形式呈現.教學中，我們一定要給學生講清其本質.只要學生理解了公式的內涵，才能達到靈活應用的目的.

視角6直接用極坐標換元，借助于判別式作答.

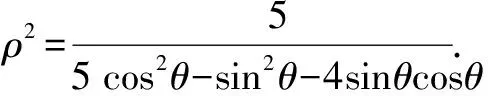
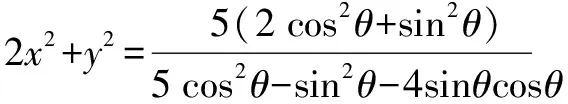
進一步換元，令2x2+y2=z，tanθ=t，化簡,得

(5+z)t2+4zt+(10-5z)=0.

由Δ=(4z)2-4(5+z)(10-5z)≥0，

得9z2+15z-50≥0，(3z-5)(3z+10)≥0.

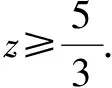
評注此解法以所要求解的結論為出發點，借助三角換元和二次函數的判別式來解決，解法相對比較新穎，可以在教學中適當展示，拓寬學生的視野和解題思路.

四、追根溯源

此題與2011年全國Ⅱ卷理科第16題有很大的相關性.

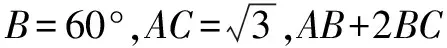
求解展示從略，有興趣的讀者可以自行查閱.

本題無論從一般換元法，還是從三角換元法入手，甚或導數法、極坐標換元法等，均可以順利解答，只是求解過程或簡單或繁瑣.當然本文所研究試題的一個顯著特點在于已知條件的左邊可以進行因式分解，所以解決起來更加便捷.

五、變式訓練

變式1 若正數a,b,c滿足(a+c)(b+c)=2，則a+2b+3c的最小值是____.(答案：4)

說明本道題的已知條件呈現的是兩個一次因式的乘積，并且是定值，明顯降低了難度，利用三角換元或極坐標換元均可以順利解決.

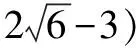
說明此題可以嘗試直接利用極坐標換元法；如果大家可以進行適當配湊(x+1)(y+2)=6，就可以利用變式1的解法求解得出結果.

變式3正數x,y滿足x2+2xy+4y2=6，求x2+4y2的取值范圍.(答案:[4,12])

說明本題不能進行因式分解，因此要考慮采用配湊法，利用三角換元解決；或直接利用極坐標換元來求解.

六、教學反思

對于一道典型題，哪怕是一道小題,我們也不能小覷.這道題可以說是小題雖小,卻能以小見大,內涵豐富.因此我們一定要弄清題目本質，還要根據不同的形式進行適當地變式訓練，通過分析選擇合適的解題方法.以期達到做一題，通一類，會一片的目的.同時，高中數學課程要以發展學生為本，啟發學生思考，引導學生把握數學知識的本質.因此，我們不能就題講題,停留在淺層次，而是要深入探討，而且還要善于總結同類問題的共性，找到此類問題的解決策略，將所學知識進行系統化.