實施單元整合重構(gòu) 實現(xiàn)數(shù)學(xué)深度理解

溫展鉅

（廣東省深圳市寶安區(qū)共樂小學(xué)）

北京師范大學(xué)劉月霞、郭華在《深度學(xué)習(xí)：走向核心素養(yǎng)》一書中指出：“深度學(xué)習(xí)，是指在教師引領(lǐng)下，學(xué)生圍繞著具有挑戰(zhàn)性的學(xué)習(xí)主題，全身心參與、體驗成功、獲得發(fā)展的有意義的學(xué)習(xí)過程。深度學(xué)習(xí)過程著眼于學(xué)生對所學(xué)內(nèi)容的整體理解，促進學(xué)生的知識建構(gòu)和方法遷移。”北師版《義務(wù)教育教科書·數(shù)學(xué)》五年級下冊“分數(shù)的再認識”單元內(nèi)容包含了整體“1”的再認識、分數(shù)單位、真假分數(shù)、帶分數(shù)、分數(shù)與除法的關(guān)系等知識，雖然對分數(shù)進行了“較全面”的再認識，但這些知識點之間的內(nèi)在聯(lián)系不夠緊密，不利于學(xué)生在學(xué)習(xí)的過程中進行“整體認識”。我在教學(xué)這一單元時，將“分數(shù)與除法的關(guān)系”與“真假分數(shù)的認識”以及“帶分數(shù)與假分數(shù)的互化”進行整合重構(gòu)，將這幾個知識點放在同一教學(xué)情境中，讓學(xué)生經(jīng)歷“操作、分類、辨析”等數(shù)學(xué)活動，體驗知識發(fā)生、發(fā)展的過程，充分感悟知識之間的內(nèi)在關(guān)聯(lián)。

一、動態(tài)情境，整合貫通

數(shù)學(xué)教學(xué)強調(diào)學(xué)生對知識的“再發(fā)現(xiàn)”與“再創(chuàng)造”，而數(shù)學(xué)情境則是數(shù)學(xué)知識“再發(fā)生”和“再創(chuàng)造”的重要載體。北師版教材中，設(shè)計了“分餅”與“分數(shù)與除法”兩部分內(nèi)容，包括“帶分數(shù)、真分數(shù)、假分數(shù)”和“分數(shù)與除法的關(guān)系、帶分數(shù)與假分數(shù)的互化”。教材中有兩個情境，前面是“分餅”，后面是“分蛋糕”，前一節(jié)學(xué)習(xí)帶分數(shù)和假分數(shù)等概念，后一節(jié)進行帶分數(shù)和假分數(shù)的互化，在認知上容易產(chǎn)生割裂。

教學(xué)實踐中，我把“分餅”的情境進行了擴充，以“唐僧師徒取經(jīng)途中化緣”的故事，動態(tài)化地呈現(xiàn)出對不同餅數(shù)進行平均分的題組，引導(dǎo)學(xué)生從整數(shù)的等分除法，過渡到分數(shù)的除法，將分數(shù)除法與整數(shù)除法打通。

師：話說唐僧師徒四人前往西天取經(jīng)，路上經(jīng)歷了各種磨難，就連每天吃飯都不容易。他們化緣得到的食物有時候多，有時候少，但他們師徒總是平均分配食物。這一天，化緣得到8張餅，分給師徒4人，平均每人得多少張餅？

生：總數(shù)是8張餅，平均分成4份，求每份數(shù)，8÷4=2（張）。

師：總數(shù)除以份數(shù)等于每份數(shù)，所以列式8÷4=2。

師：如果只有4張餅，平均分給4個人，平均每人分得多少張餅？

生：4÷4=1（張）。

師：如果只有1張餅，平均分給4個人，平均每人分得多少張餅？

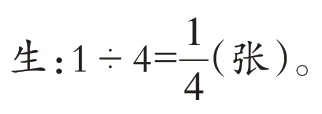
師：如果有5 張餅，平均分給4 個人，平均每人分得多少張餅？

生：5÷4=1（張）……1（張）每人分得1張餅多。

生：5÷4=1.25（張）。

在數(shù)的認識中，自然數(shù)的認識是在數(shù)的基礎(chǔ)上建立的，分數(shù)的認識是在分的基礎(chǔ)上建立的，而平均分又與除法有著緊密聯(lián)系。因此，在本課“唐僧師徒分餅”的情境中，學(xué)生借助“平均分”的熟悉模型，從整數(shù)除法過渡到了小數(shù)除法、分數(shù)除法。分得的結(jié)果從整數(shù)張到不能用整數(shù)表示，也不能用真分數(shù)表示，從而引出了學(xué)習(xí)帶分數(shù)、假分數(shù)的必要性。在這個認識過程中，不僅能分出帶分數(shù)和真假分數(shù)，還能在分的過程中發(fā)現(xiàn)分數(shù)與除法的關(guān)系，達到整合貫通的目的。同時，“平均分餅的情境”還能讓學(xué)生體會到團隊合作的重要性。此外，“艱難的取經(jīng)生活”和“虔誠的求學(xué)精神”也是對學(xué)生進行思想教育的好素材。

二、多元表征，深度理解

在前面學(xué)習(xí)的過程中，都是對真分數(shù)進行認識，把一個整體平均分成若干份，其中的一份或幾份是幾分之一或幾分之幾，而從本課開始出現(xiàn)了分子比分母大的情況，這是本課學(xué)習(xí)中的一個難點。因此，我利用操作“分餅“這一環(huán)節(jié)，讓學(xué)生建立了比一張餅再多張的表象，引導(dǎo)他們從感觀上開始認識帶分數(shù)。

師：前面我們學(xué)習(xí)過用小數(shù)表示，這節(jié)課我們一起研究用分數(shù)表示。現(xiàn)在給每個小組5 個圓片代表5 張餅，平均分成4 份，看看每份是幾張餅？請大家動手分一分。（學(xué)生小組討論、操作）

小組1：先拿出4 張餅，每人分得1 張餅；剩下一張餅再平均分成4份，每人再分得其中的1份。合起來就是1 張餅，再多張餅。（5 人小組上臺演示，1 人負責(zé)邊分邊講解）

師：大家的分法主要有兩種，一種是把每張餅都平均分成4份，每人分得每張餅的有5張餅 ，每人就分得5個就是張餅。

另一種是先分4 張，每人分得1 整張餅，再把剩下的1 張餅平均分，每人再分得張，合起來是 1 張餅再多張餅 ，可以用來表示。這里的1 表示1整張餅表示張餅表示的意思。讀作：一又四分之一，像這樣的分數(shù)叫做帶分數(shù)。你知道它為什么叫做帶分數(shù)嗎？

生：帶有整數(shù)的分數(shù)。

師：對，帶分數(shù)就是帶有整數(shù)的分數(shù)。左邊是整數(shù)部分，右邊是分數(shù)部分。它們的分法不同，得到的結(jié)果相同嗎？（指著

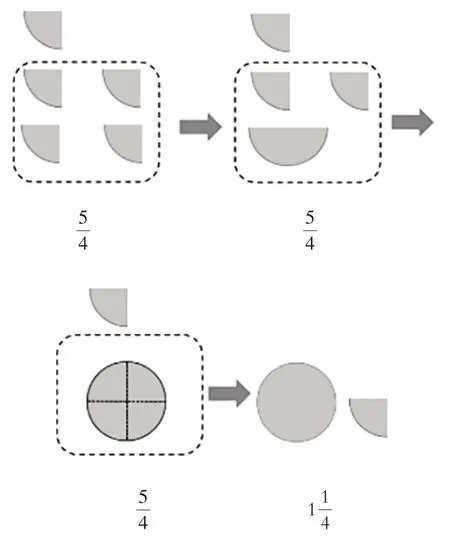
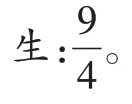
師：這是怎么得到的呢？

師：為什么要2×4＋1？

本課是在認識“真分數(shù)”“假分數(shù)”的概念前，借助“分餅”的操作過程，用不同的分法得到大小相等的兩種結(jié)果“張餅和張餅”。雖然分法不同，但學(xué)生親自參與了分的過程，自然知道兩個分數(shù)的大小相等。借助學(xué)具的操作和PPT 的演示，學(xué)生聚焦帶分數(shù)和假分數(shù)的本質(zhì)聯(lián)系是5個其中的4個可以拼成一整張餅，也就是帶分數(shù)的整數(shù)部分1，剩下就對應(yīng)的分數(shù)部分將帶分數(shù)化為假分數(shù)則是把整數(shù)部分的餅分成與分數(shù)部分相同單位的若干份，再相加。

學(xué)生在觀察、思辨的過程中，結(jié)合操作表征、圖象表征、語言表征等多種表征方式對假分數(shù)和帶分數(shù)的本質(zhì)進行深度理解，逐步建構(gòu)出帶分數(shù)與假分數(shù)互化的算理，并總結(jié)出了簡便的算法。

三、整體把握，有效建模

師：回顧分餅的過程，4÷4=1 張餅，能不能把1張餅也寫成分數(shù)呢？

師：請同學(xué)們仔細觀察我們剛才通過分餅得到的除法算式和商。你發(fā)現(xiàn)了什么？

生：除數(shù)就是分數(shù)的分母。

師：誰能明白他的發(fā)現(xiàn)？

生：被除數(shù)就是分數(shù)的分子，商就是分得的張數(shù)。

（PPT 出示，全班觀察：除法的被除數(shù)相當(dāng)于分數(shù)的分子，除數(shù)相當(dāng)于分數(shù)的分母，除號相當(dāng)于分數(shù)線，這就是分數(shù)和除法的關(guān)系）

師：A張餅平均分給B個人呢？每人分得幾張？

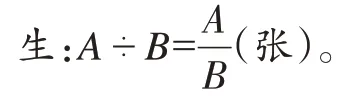
師：要滿足什么條件？

生：B不能為0，因為除數(shù)不能為0。

分數(shù)與除法的關(guān)系是連接分數(shù)意義與等分除法意義的重要規(guī)律，也是分數(shù)、整數(shù)、小數(shù)三者之間轉(zhuǎn)換的橋梁。因此，在數(shù)量上要給學(xué)生提供豐富的材料，讓他們充分體驗、感受并利用不完全歸納的方法發(fā)現(xiàn)分數(shù)與除法之間的關(guān)系。同時，在材料的類型上要包含能分出整數(shù)的、能分出分數(shù)（小數(shù)）的情況，分數(shù)中還要包含真分數(shù)和假分數(shù)。只有在類型全面的材料中，才能讓學(xué)生把學(xué)習(xí)過的關(guān)于平均分的所有除法都納入到發(fā)現(xiàn)的規(guī)律之中，從而打通了整數(shù)除法、小數(shù)除法與分數(shù)除法的聯(lián)系，進而理解了本節(jié)中分得的商，可以在整數(shù)、小數(shù)、分數(shù)之間的相互轉(zhuǎn)換，達到對分數(shù)意義的整體認識。

四、多維辨析，提升思維

北師版教材采用舉例的方式得出真、假分數(shù)的概念。學(xué)生能很快得出真分數(shù)和假分數(shù)這兩個名稱，通過教師的引導(dǎo)，也能發(fā)現(xiàn)真分數(shù)的分子和分母之間的關(guān)系以及真假分數(shù)的大小關(guān)系，但對帶分數(shù)、真分數(shù)、假分數(shù)這三個概念以及它們之間的關(guān)系區(qū)別不夠清晰。

新課教學(xué)前，學(xué)生對分數(shù)的認識不是一張白紙，有的學(xué)生在平時生活中已對真假分數(shù)有了一定的認識。課前訪談中我發(fā)現(xiàn)，有些學(xué)生只是知道真假分數(shù)的名稱，部分學(xué)生雖知道真假分數(shù)的分子和分母的大小關(guān)系，但對真分數(shù)、假分數(shù)及帶分數(shù)的分類不清晰。因此，本課需要讓學(xué)生通過對不同類型的分數(shù)進行分類、辨析，借助符號化的理解和表達，對三類分數(shù)進行深層辨析。

師：仔細觀察這些分數(shù)的特征，把下面分數(shù)進行分類，并說一說你是怎樣想的？

生：分為真分數(shù)和假分數(shù)。

師：哪些是真分數(shù)呢？

師：分子小于分母的分數(shù)叫做真分數(shù)，分子等于或大于分母的分數(shù)叫做假分數(shù)。

師：從形式上還可以把帶有整數(shù)部分的分數(shù)分為一類，不帶整數(shù)的分數(shù)分為一類。能不能把也按分子和分母的大小來分？它屬于真分數(shù)還是假分數(shù)。

生：當(dāng)a大于或等于b時是假分數(shù)，當(dāng)a小于b時是真分數(shù)。

生：當(dāng)a大于b時當(dāng)a 等于 b 時當(dāng)a小于b時

師：真分數(shù)小于1，假分數(shù)大于或等于1。

思維的獨立性意味著不為情境的暗示所左右，不人云亦云，不盲從附和，嚴格地估計思維材料和精細地檢查思維過程。思維的獨立性是批判性思維的重要特點。在本課中，我首先讓學(xué)生對課中所得出的各種不同類型的分數(shù)按不同的標準進行分類，通過分數(shù)讓學(xué)生觀察不同類型分數(shù)的特征，并在真分數(shù)假分數(shù)的分類中打破學(xué)生原有的淺層認識“帶分數(shù)不屬于假分數(shù)和真分數(shù)”，重構(gòu)對分數(shù)的分類，達到對分數(shù)分類的全面認識，培養(yǎng)了學(xué)生的批判思維能力。

本節(jié)課通過對分數(shù)與除法、真假分數(shù)帶分數(shù)等知識的整合重構(gòu)，創(chuàng)設(shè)動態(tài)化情境，促進了學(xué)生整體把握、深度理解，培養(yǎng)了批判性思維。