淺談中學數學中的探究性學習

見濤

摘要：自1909 年杜威提出探究性學習方法以來，這種全新的學習方法逐步得到世界各國教育學家的認同，最終成為世界上最具影響力的學習方法之一。本文對探究性學習的概念和起源進行了簡要的敘述，對如何實施探究性學習進行了詳細的論述，并提出了一些思考。

關鍵詞：中學數學? 探究性學習? 實驗

對于“探究性學習”，筆者認為可以這樣理解：“探”即為在沒有目標也就是心中沒底的情況下前進;“究”即為心中有一定的目的，但不知道達到這一目的要走哪條路。綜合起來就是，學生不知道怎樣摸著石頭到達河對岸。作為老師，職責就是合理地引導學生，給予學生一定的提醒和幫助，讓他們在主動“摸著石頭”的同時按照合理的方法自己發現到達“河對岸的路”。

一、探究性學習

探究性學習即學生選取某個問題作為突破點，通過各種探究活動獲得知識。探究的問題其實是開放性問題，往往所需知識覆蓋面比較廣，其綜合性探究問題較強，解答過程靈活多樣，大部分時候需要用到學科知識的基本技能、基礎知識和基本方法等，創造性思維過程也必不可缺。因此，一定要在平時注重培養和鍛煉學生的思維能力。學生在研究未知問題時會想到很多假設，這是找到解決辦法的重要途徑。

二、探究性學習的起源

美國教育家杜威是世界上最早提出在學校中使用探究性學習方法的教育者。在1909年，杜威在一次發言中表示，作為一種更有價值的學習方式，科學思考應該被教育者予以足夠的重視。杜威作為實用主義教育學家，他認為教育要從兒童的需要和興趣出發，讓興趣成為最好的老師，主動學會科學研究的過程或方法。

三、創設有利于學生開展探究性學習的良好情境

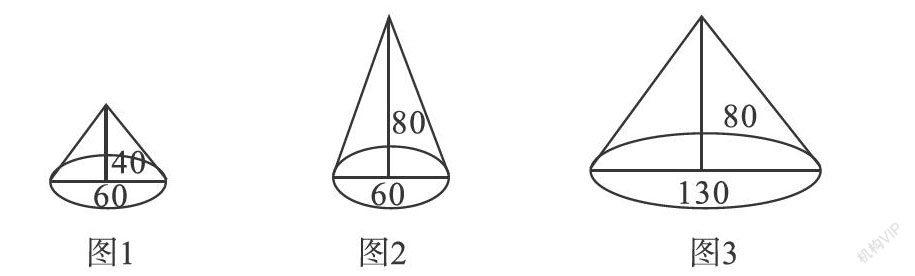
數學教學活動的進行要注重學生當下的學情，了解學生已有的知識和技能，為學生提供必要的學習交流機會。比如在圓錐體積公式的教學中，可以讓學生先觀察，發現不同，發揮自身思維的特點，找到圖形面積不同后，再讓學生互相討論由圖1如何變成圖2以及由圖1如何變成圖3。

向學生提問：“圓錐體積有沒有變化？它們的體積變化跟哪些因素有關呢？”因此，怎樣計算圓錐的體積就成為學生自主探究的主要目標。

（一）讓自主探究成為學生實踐活動的主旋律

《普通高中數學課程標準》重點指出：“學生的學習活動應該遵循學生的身心發展規律以及知識的可接受能力來規劃。”在日常的課堂教學中，教師要創設有利于開展探究性學習的條件，讓學生盡可能多地解決具有引導性的問題，培養學生獨立思考能力，以達到提高學生的自主探究能力的目的。

在教學中不僅僅可以借助外部力量以激發學生的濃厚學習興趣，還可以結合問題與圖形之間的關系引起學生的學習興趣，讓學生自發地去研究、去思考，最后掌握知識。利用數學問題模型開展教學活動，如在學習立體幾何的時候，剛接觸立體圖形的學生們可能還不能理解抽象的空間物體，這時候老師可以引導學生觀察課本、水杯、粉筆等常見物體，數一數它們有幾個面、幾條邊，它們從側面、正面、上面觀察是什么樣的平面圖形等。利用可見的物體，將其與所需要學習的數學知識結合起來，讓同學能更清晰地了解數學知識，體現了數學中常用的數形結合的思想。

（二）讓學生自主探究問題的答案

積極調動學生自主探究問題，培養學生運用知識的靈活性，使其敢于挑戰和解決陌生的問題。

例：已知sn是等比數列的前n項和，s9是s3與s6的等差中項，求證：a2，a8，a5成等差數列。

解：因為s3，s6，s9成等差數列，所以s3+s6=2s9且q≠1

則

a1（1-q3）1-q+a1（1-q6）1-q=2a1（1-q9）1-q

計算得：

1+q3=2q6

a2+a5=2a8

所以a2，a8，a5成等差數列。

四、探究性學習實例

在講解“三角形全等判定知識”時，上課之前先精心準備一些器材，用一個大家熟悉的生活現象創設問題情境，引起學生的興趣，從而引入新課。接著讓學生做實驗，具體過程如下。

（一）課題提出

1.指導學生

用剪刀在紙上剪出兩個全等三角形：以一個三角形作為模板，剪出的另一個三角形與原三角形是全等的。

2.引入課題

提問：我們知道用剪刀可以剪出兩個全等三角形，那么能不能用數學的方法，也就是所學的尺規作圖的方法作出一個三角形與原三角形全等呢？

（二）現象觀察

引導學生猜想：要作出兩個三角形全等需要幾個條件？

提問：如果只給出一條邊、一個角或者兩條邊、兩個角能不能作出一個三角形與原三角形全等？

（1）指導學生操作;

（2）學生報告操作結果;

（3）老師黑板演示。

（三）深入探究

在上面所給出的條件中，為什么都不能作出一個三角形與原三角形全等？如作出全等三角形還需要哪些條件？

淺談中學數學中的探究性學習

2021年7月下 第21期 （總第85期）

（四）原理討論

三角形是由三個角和三條邊組成的，如果只知道其中一個角或兩個角，不能夠確定三角形的邊，同樣如果只知道其中的一條邊或兩條邊，也不能確定三角形的角。

引導學生分析討論：要增加什么條件？

得出結論：知道了兩個角相等，如果再知道它們的夾邊相等，則可以作出一個三角形與原三角形全等。

追問：如果知道有兩條邊和一個角相等，能不能作出一個三角形與原三角形全等呢？

（五）學生討論并動手操作

得出結論：不一定能夠畫出一個三角性與原三角形全等，具體可分為以下兩種情況：

1.如果是知道兩邊和其中一邊的對角與原三角形全等，就不能作出一個三角形與原三角形全等。

如上圖，雖然知道了AB=A′B′，BC=B′C′，∠A=∠A′，但是我們也能作出另一條邊B′D與BC相等，顯然△ABC與△A′B′D是不全等的。

2.如果知道兩邊和它們的夾角與原三角形全等，則能作出一個三角形與原三角形全等。在多媒體上用尺規作圖的方法演示。

（六）總結本節課所學的三角形判定定理

（1）如果有兩個角及其夾角與原三角形相等，則三角形全等。

（2）如果有兩條邊及其夾角與原三角形相等，則三角形全等。

注：在（2）中，如果知道兩邊和其中一邊的對角相等，則不能夠判定兩個三角形全等。

綜上所述，探究性學習就是要充分調動學生的積極性和主動性，讓學生在產生問題，有了求知欲后探討、合作交流，在老師的指導下，自主得出問題的答案。這種學習模式要求師生互動，以教材為抓手，探索未知，解答謎題。

參考文獻：

[1]陸璟.研究性學習及基本特征[J].教育發展研究，2009（10）.

[2]中華人民共和國教育部.普通高中數學課程標準[M].北京：人民教育出版社，2003.