Arduino安全遞歸調用

樂萬德， 劉舟洲， 曹敬馨， 初建杰

（1.西安航空學院計算機學院，西安710077；2.西北工業大學工業設計與人機功效工信部重點實驗室，西安710072）

0 引 言

作為一款便捷靈活的開源電子原型平臺，Arduino得到了廣泛的應用，比如汽車并線輔助系統［1］、智能防盜系統［2］，制作機械書畫手臂［3］、智能盆栽養護瓶［4］等。Arduino在高校創新創業教育中也發揮著越來越重要的作用，不僅用于案例教學［5］，參與競賽活動［6］，還用于實驗調試［7］、實驗室管理［8］等，也有學者研究其生態擴充［9］。

遞歸算法在數學和計算機領域都占據著十分重要的地位。在計算機領域，遞歸函數由于邱奇-圖靈定理顯示出重要意義［10］，邱奇-圖靈論題告訴我們一切可計算過程都可以用圖靈機模擬，1935年丘奇論題提出著名的“算法可計算函數都是遞歸函數”。同時遞歸函數是C語言等計算機編程中的一個重點和難點，國內外對于遞歸函數的教學進行了廣泛的研究。Rinderknecht［11］在廣泛研究遞歸在編程語言中出現及被程序員采用的歷史之后，提出了遞歸的課程方法。文獻［12-14］中對C語言中遞歸函數的教學方法、教學設計、微課等教學形式進行了探討。

與某些單片機有限支持甚至不支持遞歸調用不同，Arduino支持遞歸調用。而前述文獻雖然分別對于Arduino與遞歸進行了廣泛的研究，但Arduino內存有限，遞歸算法在Arduio系統中棧溢出隱患問題鮮有研究。本文旨在探索Arduino安全遞歸調用，以期進一步釋放Arduino應用潛能。

1 實驗環境

本文實驗硬件為目前廣泛應用的Arduino UNO R3。作為Arduino平臺的參考標準模板，UNO的處理器核心ATmega328，具有14路數字輸入／輸出口（其中6路可作為PWM輸出）、6路模擬輸入、SRAM 2 KB［15］。Arduino板通過USB與筆記本電腦相連。軟件開發平臺為Arduino IDE 1.8.9。

2 問題引入

在Arduino IDE輸入圖1所示代碼，編譯、下載到Arduino UNO后，在PC端打開串口監視窗口。

圖1 不安全的Arduino遞歸調用

如圖1（a）所示，在串口監視窗口可以看到，在Arduino UNO里用遞歸調用算法可以求出sum（1，2，…，500）的正確結果為125 250，沒有發生棧溢出。

作為對比，把上面的代碼稍作修改，即把上面else分支中return n＋sum（n－1）語句改為：

unsigned long temp＝sum（n－1）；

return n＋temp；

重新編譯、下載，在圖1（b）中串口監視窗口中顯示異常，沒有得到期望的結果，顯然發生了遞歸棧溢出。

由此可見，Arduino UNO在編譯時對遞歸調用在某些場景做了優化，使遞歸調用棧可以重復利用，從而避免棧溢出，但不是所有遞歸都進行了優化。因此，有必要對Arduino遞歸調用進行研究，以便對Arduino進行安全遞歸調用。

3 安全遞歸實驗設計

安全遞歸調用要解決兩個基本問題，一是要設計出正確的遞歸算法；二是要防止遞歸調用棧溢出。

3.1 遞歸算法

遞歸算法具有兩個明顯的特點：①一個更大規模的問題可以轉換成一個規模更小的同樣問題的求解，即問題的遞推性。②當一個問題轉換到某個規模足夠小的問題時有確定的解，即問題的收斂性，也即遞推終止條件。

以階乘為例，要求n！，可以把問題轉換成n*（n－1）！，即只需要求出（n－1）！這就是遞推關系，即特點一。遞推到足夠小比如1！為1是確定的，第2個特點即遞歸終止條件滿足。

一旦識別出上述兩個特點，不難編寫出遞歸程序，通常只需要將上述兩個條件映射為遞歸程序判斷結構的兩個分支。

3.2 遞歸棧溢出

遞歸算法需要注意的第2個問題是遞歸棧溢出的問題，即本文研究的重點。遞歸調用本質上是函數調用，涉及到函數參數及函數返回地址等壓棧。遞歸調用層數過多，棧地址與堆地址就會發生碰撞，也叫棧溢出。棧溢出會導致程序工作異常，需要避免。Arduino UNO的RAM內存空間只有2 KB，在掌握遞歸算法的基礎上，更要關注遞歸棧溢出問題。

3.3 實驗原理

3.3.1 AVR遞歸調用棧

Arduino UNO采用AVR ATMega328作為芯片平臺。AVR芯片的SRAM存儲示意圖如圖2所示。主要包括靜態數據區、堆空間和棧空間。其中靜態數據區和堆空間占據著低地址空間，且自下而上生長。而棧空間占據著高地址空間，且自上而下生長，主要應用于快速便捷地保存臨時數據、局部變量和中斷調用或子程序調用的返回地址。棧在系統程序的設計和運行中起著非常重要的作用，只要程序中使用了中斷和子程序調用，就必須在SRAM空間建立棧空間，并正確地設置棧指針寄存器SP。

圖2 Arduino SRAM中的存儲示意圖

當執行PUSH指令，1 byte的數據被壓入棧，棧指針（SP中的數據）將自動減1；當執行子程序調用指令CALL或CPU響應中斷時，硬件會自動把返回地址（16位數據）壓入棧中，同時將棧指針自動減2；反之，當執行POP指令，從棧頂部彈出1 byte的數據，棧指針將自動加1；當執行從子程序返回或從中斷返回指令時，返回地址將從棧頂部彈出，棧指針自動加2。

由于AVR的棧是向下增長的，即新數據進入棧時棧頂指針的數據將減小，所以隨著棧空間和堆空間的增長，剩余內存會不斷減小，甚至內存耗盡，發生棧溢出。

3.3.2 安全遞歸調用算法

如果在每次遞歸調用之前都能清楚地知道剩余內存的情況和本次遞歸調用所需內存，就可以有效防止內存耗盡及棧溢出情況。關于Arduino剩余動態內存的查看，可參考文獻［16］，本文采用圖3所示的算法來探測并規避遞歸調用棧溢出。

圖3 Arduino剩余內存探測

圖3所示的算法實現為函數，命名為availableMemory。在程序研發或者debug過程中，將availableMemory函數置于遞歸函數中，如果遞歸調用深度過深，內存可能耗盡，availableMemory返回的內存就會接近0。當剩余內存小于單次遞歸調用所需的內存，則告警并記錄遞歸調用最大深度后安全返回。

Arduino安全遞歸調用算法如圖4所示。在算法中設置一個遞歸調用狀態參數State，初始化State為1，表示遞歸狀態正常。每次遞歸調用時通過availableMemory計算剩余內存，如果剩余內存小于預設閾值，則將State變量設置為0，表示遞歸有棧溢出風險，即遞歸狀態異常。每次遞歸調用時先查看State，只有當State為1才進行進一步的包括遞歸調用在內的后續操作，這樣就妥善處理了棧溢出異常。最小閾值M1可以設置為每次遞歸調用需要消耗的內存。因為每次遞歸調用的壓棧過程都是從高地址向低地址順序壓棧的，對于單次遞歸調用所消耗的內存M1，可以就兩次遞歸調用同一個變量的內存地址相減得到。

圖4 Arduino安全遞歸調用算法流程圖

4 Arduino典型遞歸實驗

4.1 Arduino階加遞歸實驗

常見的入門遞歸實例是求階乘，隨著n的增加，階乘的結果迅速變大，容易造成存放其結果的數據類型越界。為了實驗Arduino的遞歸支持能力，本文將乘改為加，設計了一個用遞歸算法實現從1～n求和的遞歸程序，稱之為階加。階加的遞推公式及終止條件如下：

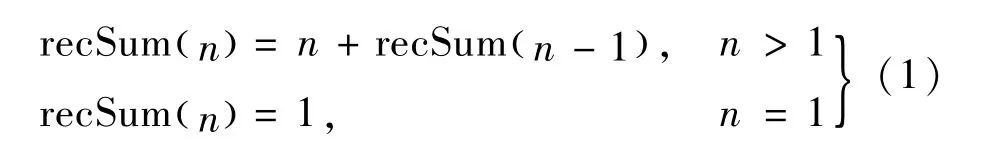
階加的遞歸調用算法與階乘的遞歸調用算法類似，以n＝4為例，其遞歸調用棧入棧出棧如圖5所示。遞歸算法中，recSum（4）需要做函數調用，其參數及函數返回地址入棧，同理recSum（3）、recSum（2）、recSum（1）也需做遞歸調用并依次入棧，此時入棧全部結束，遞歸調用棧如圖5（a）所示。

圖5 n為4時階加遞歸調用棧分析

recSum（1）＝1為遞歸終止條件，函數返回并出棧，此時recSum（2）＝2＋1也為已知，recSum（2）函數返回并出棧，同理recSum（3），recSum（4）依次返回并出棧，此時棧空間為空，如圖5（b）所示。

由圖5可見，如果參數n足夠大，recSum（n）遞歸調用時可能發生棧溢出。此時應該結束遞歸調用安全返回，并給出遞歸調用的最大深度提示。

用本文安全遞歸調用算法運行結果如圖6所示。圖6（a）是參數為300時程序運行的部分結果，當n逐層遞歸減到90時，剩余內存為15 bytes，本次遞歸調用后剩余內存已經不能繼續進行本次遞歸調用了，給出錯誤提示，并給出根據本次計算得到的最大遞歸深度為211。圖6（b）為按提示的最大遞歸深度211，計算1＋2＋…＋211的結果為22 366，計算結果正確。

圖6 階加Arduino安全遞歸調用運行結果

4.2 Arduino斐波那契數列遞歸實驗

斐波那契數列又稱黃金分割數列、兔子數列，由數學家萊昂納多·斐波那契（Leonardoda Fibonacci）提出，具有很多有趣的性質和應用。其遞推公式可由下式表示：

與階加相比，斐波那契數列遞歸算法略顯復雜。主要的不同是，第n項的值不僅僅與第n－1項有關，還與第n－2項有關。其遞歸調用棧的入棧、出棧的關系也更為復雜。以4項斐波那契為例，對應式（2）的遞歸調用的出棧入棧如圖7所示，更多項數的出棧入棧關系類似。

圖7（a）中為了求Fib（4），需要進行遞歸調用，所以需要將參數n＝4及其函數返回地址入棧，同理當n＝3，n＝2時繼續遞歸調用并將對應參數和函數返回地址壓棧，因為Fib（2）＝1為已知，可以直接返回，第1輪壓棧結束。圖7（b）中Fib（2）返回彈棧后Fib（3）＝1＋Fib（1），Fib（3）不能繼續彈棧，第1輪彈棧結束。圖7（c）、（d），圖7（e）、（f）分別進行第2、第3輪入棧出棧，分析類似，不再贅述。

圖7 n為4時斐波那契遞歸調用棧分析

由圖7可以看出，如果參數n足夠大，在某輪入棧時，可能發生棧溢出，此時應該結束遞歸調用返回，并給出遞歸調用的最大深度提示。

用本文安全遞歸調用算法運行結果如圖8所示。圖8（a）是參數為300時程序運行的部分結果，當n逐層遞歸減到161時，剩余內存為23 bytes，本次遞歸調用后剩余內存已經不能繼續進行本次遞歸調用了，給出錯誤提示，并給出根據本次計算得到的最大遞歸深度為140。圖8（b）為按提示的最大遞歸深度140，遞歸調用正常。

圖8 斐波那契Arduino安全遞歸調用運行結果

4.3 Arduino漢諾塔遞歸實驗

漢諾塔問題是遞歸算法處理的經典問題。其問題可以描述為：初始狀態下A座上有n個盤子，盤子大小不等，大的在下，小的在上。要求把這n個盤子從A座移到C座，但規定每次只允許移動一個盤，且在移動過程中在3個座上都始終保持大盤在下，小盤在上。在移動過程中可以利用B座。

這是一個非數值解問題，也蘊含著遞推關系，雖然不容易用遞推公式，但可用下面的流程圖來表達這種遞推關系。Hannoi（n，x，y，z）中n為盤子的數量，x、y、z為座子變量，取值可能為A、B、C座中的一個。表示將n個盤子從x座移動到z座上，y座可以作為中轉。當盤子的數量n＞1時，需要將n－1個盤子先從x座移到y座上（通過z座中轉），然后將x座上剩余的一個盤子移動到z座上，最后將n－1個盤子從y座移到z座上（通過x座中轉）。如果n＝1，則滿足遞歸終止條件，直接將這1個盤子從x座移到z座上。

由圖9可見，漢諾塔的遞歸調用從n階到n－1階的過程中具有兩次遞歸調用，因此其入棧出棧也比較復雜，以3個盤子的漢諾塔遞歸調用為例，分析其入棧出棧關系如圖10所示。更多項數的出棧入棧關系類似。

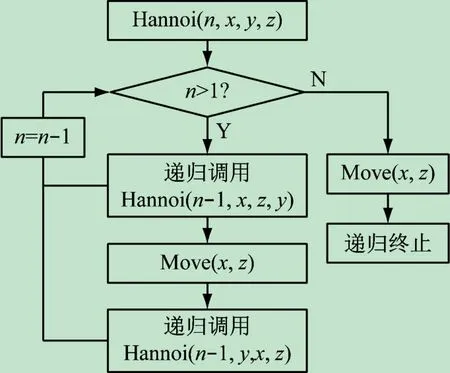
圖9 漢諾塔遞歸調用算法

圖10 n為3時漢諾塔遞歸調用棧分析

用本文安全遞歸調用算法運行結果如圖11所示。圖11（a）為參數為300時程序運行的部分結果，當n逐層遞歸減到148時，剩余內存為16 bytes，本次遞歸調用后剩余內存已經不能繼續進行本次遞歸調用了，給出錯誤提示，并給出根據本次計算得到的最大遞歸深度為153。圖11（b）為按提示的最大遞歸深度153，遞歸調用正常。

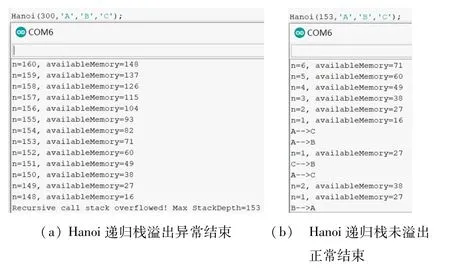
圖11 漢諾塔Arduino安全遞歸調用運行結果

5 結 語

為了防止遞歸調用棧溢出帶來的災難性后果，本文為Arduino遞歸調用設計了防溢出的遞歸調用算法。無論是在簡單階乘（階加）遞歸調用，還是在相對復雜的斐波那契數列、漢諾塔遞歸調用中，算法都穩定可靠。在Arduino實踐中，為安全遞歸調用提供了保障，為Arduino創新應用提供更豐富的手段。