城市管道泄漏次聲波傳播影響機制模擬分析

郝永梅， 姚 強， 蔣軍成， 邢志祥， 許 寧

（1.常州大學環境與安全工程學院，江蘇常州213164；2.常州港華燃氣有限公司，江蘇常州213161）

0 引 言

城市管網輸送系統運行安全及泄漏問題直接影響城市運行安全。近年來，全國主要城市管網泄漏事故頻發，給城市安全發展帶來威脅。由于管道泄漏對管道運行參數幾乎沒有影響，信號特征不明顯，尤其在嘈雜的城市中，難以被及時檢測發現［1］。而城市管網多敷設于人口集中區域，穿越建筑物，一旦發生火災爆炸，人員、財產損失大，社會影響惡劣。因此，研究管道泄漏技術，及時檢測發現管道泄漏對城市安全發展及社會穩定都具有重要意義。

城市管網泄漏引發的振動與噪聲處于同一頻帶，因此管道泄漏檢測的難點在于如何從城市特有的復雜環境噪聲中提取有用的泄漏信號［2］。次聲波法檢測技術具有檢測成本低、傳播距離長、易識別等優點［3］，國內外目前已在管道泄漏檢測、地震、火山預測等方面有著初步應用。于海濤等［4］通過對管道次聲波泄漏監測系統優化設計，提高次聲波泄漏監測系統的定位精度和抗干擾能力，實現了對3 mm泄漏點的可靠檢測和定位；朱衛東等［5］通過對長輸管道和海底管道的管道泄漏次聲波監測系統開發，實現了50 km系統監測距離內低誤報率、低漏報率，可以監測3 mm孔徑的泄漏，定位誤差可達±20 m以內；武偉強等［6］利用基于硬件的雙傳感器檢測方法，利用次聲波對輸油管道泄漏的檢測與定位；闞玲玲等［7］基于聲學和流體學等相關理論，研究天然氣管道發生泄漏時次聲波產生的機理及信號特點和采集方法，得到了天然氣管道泄漏檢測系統的軟、硬件設計方案。Blom等［8］提出了一種改進的Bayes區域次聲定位算法，描述定位源的后驗密度函數的精度；Matoza等［9］提出了一種基于地震傳感器和次聲傳感器采集信號相位相關和相干性的分析方法，實現火山的預測，但對于研究火山持續噴發過程中次聲波的特征還未深入探索；Dragomiretskiyk等［10］針對次聲波信號精度不高的問題，提出VMD算法來提高次聲信號的處理方法和精度；Cannata等［11］用小波變換相干聯合分析方法證明了地震和火山噴發的預測是可行的，但實驗精度還需要進一步提高。

以上研究不同程度對次聲波信號及其應用進行探索，促進了次聲波檢測技術的發展，但在管道泄漏檢測方面，尤其是針對城市管道泄漏次聲波信號的傳播機制的研究很少，缺乏準確全面的研究。本文基于流體力學和聲學原理，通過使用COMSOL軟件進行模擬，利用有限元法和流體力學計算公式，以聲壓級作為次聲波能量的衡量標準對城市管道次聲波泄漏信號的傳播因素及其影響機制展開研究。

1 泄漏次聲波傳播影響因素及作用機理

次聲波是由機械振動產生的頻率小于20 Hz的極低頻機械波，具有傳播距離長、穿透能力強和衰減小的特點。其中頻率低于10 Hz的次聲信號適用于管道泄漏監測，有利于管道泄漏信號的監測和接收［12］。次聲波的傳播能量和速度在管道中傳播易受諸多因素影響，主要影響因素有泄漏孔徑、馬赫數、管道壓力和介質。

1.1 泄漏孔徑對次聲波傳播的影響

管道泄漏孔徑對次聲波傳播的影響較大。PCCP水管泄漏試驗［13］表明，隨著泄漏孔徑的增大，次聲波所屬的低頻段受泄漏孔徑的影響更明顯，傳播平面波，且出現了駐波的波腹與波節。

王黎宏［14］認為基于次聲波傳感的泄漏檢測技術可以在一定運行壓力的油氣管道上進行應用，檢測距離與管道運行破壞孔徑的大小有關，在其他條件都不變的條件下，聲壓波動值以及聲壓級隨泄漏孔徑的增大而增大。

1.2 壓力對次聲波傳播的影響

管道壓力對次聲波的傳播有著重要影響，在其他條件一定時，管道的壓力越大，單位時間流體泄漏量越大。管道壓力對次聲波傳播影響可通過對管道的流動方程和水平管道流動模型韋茅斯方程簡化來表達，摩擦因數增大，導致泄漏孔處的振動加強，再由次聲波的產生機理可知，振動會產生聲波。振動加強也就產生了能量更大的聲波［15］。壓力對次聲波傳播的影響可由下式表達：

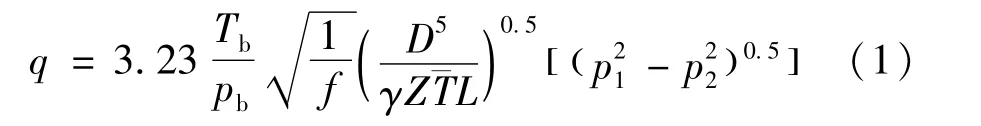
式中：q指流體流速，m／s；Tb是溫度，K；pb是壓力，MPa；f是摩擦因數；γ是氣體重力，N；Z是氣體壓縮系數；ˉT是氣體平均溫度，K；L是管道長度，mm；D是管道管徑，mm；p1是進口段壓力，MPa；p2是出口段壓力，MPa。

本文采用有限元法分析計算，運用簡化的雷諾平均納維-斯托克斯描述管道網絡中流體的運動，并對速度和壓力場取時間平均值［16］。聲壓級計算公式可由下式表達：

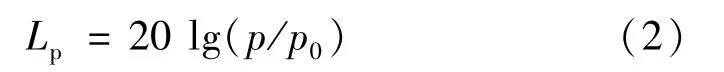
式中：Lp為聲壓級大小，dB；p為聲壓，MPa；p0為基準聲壓，MPa。

1.3 介質對次聲波傳播的影響

介質密度次聲波的傳播速度隨著介質密度的變化和氣體壓縮系數的變化而變化，且流體介質的密度越大，振動頻率也越大，從而增大次聲波的能量。介質對次聲波傳播的影響可由下式表達：

式中：Q為單極源強度，1／s2；ρ0為流體介質密度，kg／m3；m為偶極源，N／m3；ω為角頻率，rad／s；c為次聲波在介質中的傳播速度，m／s。

1.4 馬赫數對次聲波傳播的影響

馬赫數可以用來表征流體可壓縮程度。氣體泄漏所產生的馬赫數與氣體管道泄漏孔處的靜態壓力有一定的關系［17］。天然氣管道的初始壓力對管道泄漏孔處的靜態壓力有著決定性的作用。馬赫數對次聲波傳播的影響可由下式表達：

式中：u是天然氣管道泄漏孔附近的氣體流動速度，m／s；Ma表示馬赫數；k表示天然氣的等熵指數，在常溫下可近似為定值1.29；T′表示管道泄漏孔附近溫度，K。

2 數值模擬

根據城市管道特點，結合試驗管道，設計仿真模擬管道規格為φ63 mm×4.7 mm，長10.16 m，管道材質為PE管，距離管道進氣段4.5 m處設置一個泄漏孔模擬單孔泄漏，距離進氣段和出氣段4.5 m處分別設置泄漏孔模擬雙孔泄漏情況。

對流體速度、無壁面滑移以及壓力設置，設置出口面、入口面，其余為壁。初始流速為7 m／s；溫度為293.15 K，下方為壓力出口，設置其為管道內壓；考慮管道邊界層，選擇剪切銳邊處理，平滑地過渡到其內部網格，進行4次迭代，處理最大單元深度為6 mm。采用非結構化的幾種不同形狀相結合進行區域劃分。本文對泄漏孔及鄰近區域采用密度盒加密處理，保證計算結果的收斂性。壁處理采取壁函數方式，出口則采用抑制回流，同時考慮重力影響。管道泄漏模擬見圖1。

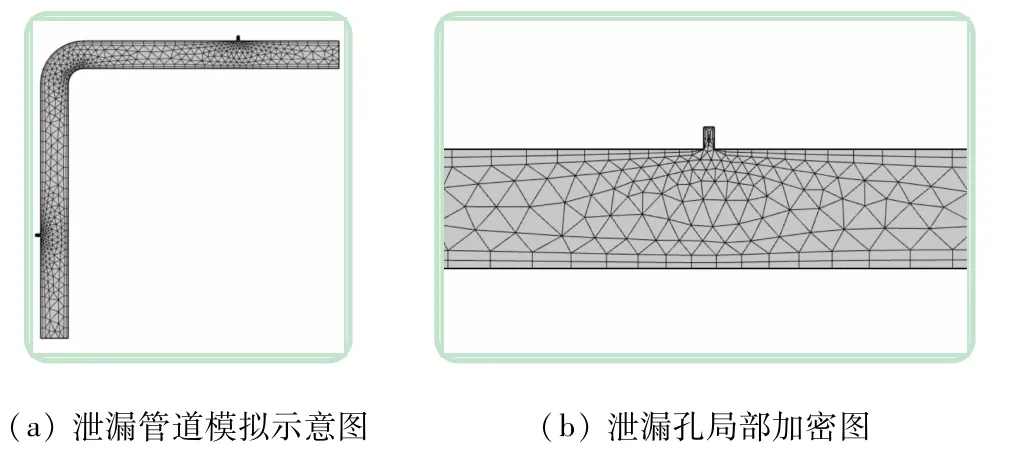
圖1 管道泄漏模擬圖

3 泄漏次聲波傳播影響因素模擬

3.1 泄漏孔徑對次聲波傳播的影響

本實驗模擬單孔、雙孔泄漏管道，管道介質為空氣，壓力設置為0.1 MPa。泄漏孔徑分別設置1、3、5、9 mm。實驗模擬結果如圖2所示。

圖2 不同泄漏孔徑聲壓級變化圖

3.2 壓力對次聲波傳播的影響

根據城市中低壓管道實際壓力，管道介質為空氣，分別在管道壓力0.01、0.1、0.3 MPa下，用2 mm小孔泄漏和7 mm中孔泄漏進行模擬比較。部分模擬結果如圖3所示。

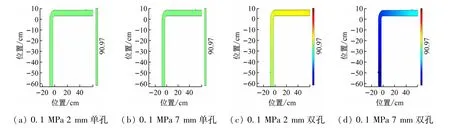
圖3 不同壓力下聲壓級變化圖

3.3 不同介質對次聲波傳播的影響

管道介質為水，分別在管道壓力0.01、0.1、0.3 MPa下，通過2 mm小孔泄漏和7 mm中孔泄漏情況與介質為空氣時管道泄漏情況進行對比研究。部分模擬結果如圖4所示。

圖4 不同介質中聲壓級變化圖

3.4 馬赫數對次聲波傳播的影響

管道介質為空氣，分別在0.1、0.2、0.3 Ma下，對于2和7 mm單、雙孔泄漏進行研究。部分模擬結果如圖5所示。

圖5 不同馬赫數下聲壓級變化圖

4 模擬結果分析

（1）泄漏孔徑對次聲波傳播影響規律。單、雙孔泄漏聲壓級數值隨著孔徑的增大總體呈增大趨勢；單孔泄漏管道孔徑＜3 mm時，聲壓級數值變化比較平緩，當繼續增大泄漏孔孔徑，聲壓級數值變化呈增大趨勢；雙孔泄漏管道孔徑＜3 mm時，聲壓級變化呈增大趨勢，當繼續增大泄漏孔孔徑，聲壓級增大的趨勢明顯減緩［見圖6（a）］。

（2）壓力對次聲波傳播影響規律。小、中孔泄漏聲壓級數值隨管道壓力的增大總體呈增大趨勢；中孔泄漏聲壓級數值大于小孔泄漏聲壓級數值。單孔泄漏實驗中，不同壓力下，泄漏管道聲壓級數值總體呈增大趨勢，但變化比較平緩，聲波的特征頻率無太大變化；雙孔泄漏實驗中，不同壓力下，泄漏管道聲壓級數值總體呈增大趨勢，且變化幅度較明顯［見圖6（b）］。

（3）介質對次聲波傳播影響規律。單孔泄漏模擬中，在流體為水的管道中，當管道壓力較小時，泄漏管道聲壓級數值增長幅度較平緩，當管道壓力大于0.1 MPa時，聲壓級數值變化幅度較明顯。而當管內流體為空氣時，當管道壓力較小時，泄漏管道聲壓級數值變化幅度較明顯，當管道壓力大于0.1 MPa時，聲壓級數值增長幅度放緩。當流體為空氣時，次聲波信號傳播受壓力的影響較大；管道內介質變化對次聲波傳播能量的影響不明顯；次聲波在介質為水的管道比介質為空氣的管道傳播信號強［見圖6（c）］。

（4）Ma對次聲波傳播影響規律。單、雙孔泄漏時聲壓級數值隨著Ma的增大總體呈增大趨勢。單孔泄漏管道中，孔徑較小，Ma＜0.2時，聲壓級增長幅度較平緩，當繼續增大Ma，聲壓級增大幅度較快；當孔徑較大，Ma＜0.2時，聲壓級增長幅度較快，當繼續增大Ma，聲壓級增大幅度放緩。雙孔泄漏管道中，聲壓級變化幅度隨Ma增大呈加快趨勢。在單孔泄漏實驗中，Ma大小的變化對次聲波傳播的影響較明顯；雙孔泄漏實驗中，Ma變化對聲壓級影響較小；特征頻率隨Ma的增大呈增大的趨勢［見圖6（d）］。

圖6 聲壓級數值圖

5 結 語

本文基于計算流體力學和聲學理論，采用有限元法分析計算，使用COMSOL軟件對管道進行模擬和實驗，研究管道次聲波泄漏信號的傳播能量與影響因素之間的關系得出以下結論：

（1）管道泄漏孔徑越大，采集到的次聲波泄漏信號強度越大。由此得出管道泄漏孔徑對次聲波傳播的影響呈正相關；小孔泄漏聲壓級的值總體上小于中孔泄漏聲壓級的值；雙孔泄漏比單孔泄漏更易受次聲波傳播影響因素的影響。

（2）管道內的壓力大小對次聲波傳播的影響相對較小；次聲波泄漏信號在水管道中的傳播能量比在空氣管道中傳播能量更大；次聲波信號的強度和特征頻率隨著Ma的增大呈增大趨勢。

（3）在軟件模擬研究中也發現，管道彎頭、三通等管道對研究次聲波傳播機制帶來了困難。因此，今后可進一步找出管道彎頭、三通對次聲波影響的規律，從而消除管道彎頭、三通等對研究次聲波傳播機制帶來的干擾。