基于Matlab/Simulink的PI調(diào)節(jié)器建模分析與限幅特性仿真研究
張厚升, 朱勝杰, 邢雪寧, 杜欽君, 趙艷雷
(山東理工大學(xué)電氣與電子工程學(xué)院,山東淄博255000)
0 引 言
對于自動控制系統(tǒng)來說,系統(tǒng)的穩(wěn)態(tài)精度和動態(tài)性能指標(biāo)常常是互相矛盾的[1-2],依據(jù)自動控制理論,要解決這個矛盾,必須設(shè)計合適的動態(tài)校正裝置,用來改造系統(tǒng)。動態(tài)校正的方法較多,對于一個自動控制系統(tǒng)來說,能夠符合要求的校正方案也不是唯一的。在自動控制系統(tǒng)中,對于帶電力電子變換器的直流閉環(huán)調(diào)速系統(tǒng)[3-4],傳遞函數(shù)階次比較低,一般采用PI調(diào)節(jié)器[5-8]就能完成系統(tǒng)動態(tài)校正的任務(wù)。
許多初學(xué)習(xí)者對于PI調(diào)節(jié)器的特性理解不夠深入,尤其是在采用Simulink進行自動控制系統(tǒng)建模仿真的時候[9-10],調(diào)試的過程中出現(xiàn)問題最多的也是PI調(diào)節(jié)器,甚至得不到正確的仿真波形。通常,利用Matlab/Simulink對PI調(diào)節(jié)器進行建模有幾種不同的形式[11-12],比較常見的一種是基于PI調(diào)節(jié)器傳遞函數(shù)建立的仿真模型,另一種是帶積分限幅的PI調(diào)節(jié)器仿真模型,對于這些不同的仿真模型,很少有人去關(guān)心其特性,只是根據(jù)PI調(diào)節(jié)器建立相應(yīng)的系統(tǒng)仿真模型并進行仿真,仿真結(jié)果有時候會存在一些問題,卻找不到原因。本文旨在對采用PI調(diào)節(jié)器傳遞函數(shù)仿真模型和帶積分限幅的PI調(diào)節(jié)器仿真模型進行特性分析與建模仿真,研究其性能上的差異,以便使用者在進行自動控制系統(tǒng)Simulink仿真建模時選擇合適的PI調(diào)節(jié)器模型及其參數(shù)。
1 PI調(diào)節(jié)器的傳遞函數(shù)與特性分析
依據(jù)控制理論的相關(guān)知識,比例控制具有控制的快速性,但只能實現(xiàn)系統(tǒng)的有靜差調(diào)節(jié);積分控制可以實現(xiàn)系統(tǒng)的無靜差控制,但系統(tǒng)的快速性卻較差,如果要實現(xiàn)系統(tǒng)的穩(wěn)態(tài)精度高,同時又要實現(xiàn)動態(tài)響應(yīng)快,可以把比例和積分兩種控制結(jié)合起來[1-2],即采用PI調(diào)節(jié)器,實現(xiàn)系統(tǒng)的無靜差快速調(diào)節(jié)[13]。
PI調(diào)節(jié)器的輸出由比例和積分兩個部分疊加而成,其輸入-輸出的關(guān)系可以描述為
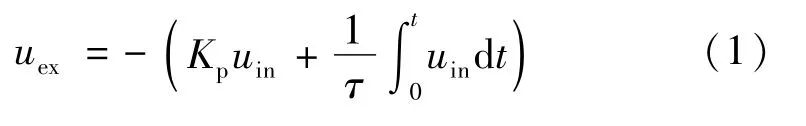
式中:Kp為PI調(diào)節(jié)器的比例放大系數(shù);τ為PI調(diào)節(jié)器的積分時間常數(shù)。
PI調(diào)節(jié)器的傳遞函數(shù)可以表示為[1-2]:
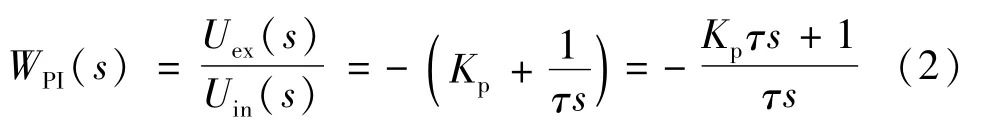
如果令Ti=Kpτ,則PI調(diào)節(jié)器的傳遞函數(shù)也可以表示為
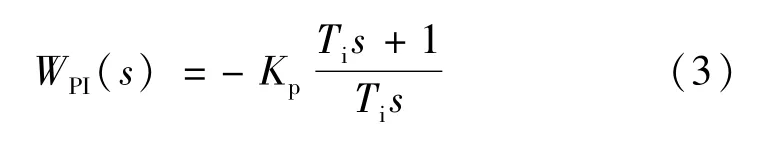
或者
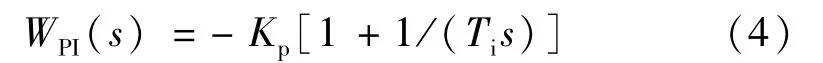
式中,Ti是微分項中的超前時間常數(shù)。這里需要注意,Ti和積分時間常數(shù)τ的物理意義是不同的。
依據(jù)式(3)、(4),可以用Simulink建立兩種不同的PI調(diào)節(jié)器仿真模型,但是這兩種仿真模型的效果是不一樣的,后文將會展開深入研究。
采用模擬控制時,在自動控制系統(tǒng)中,常用的PI調(diào)節(jié)器可以用運算放大器來實現(xiàn),如圖1所示(采用數(shù)字控制時的基本原理類似,本文以模擬控制為主進行分析)。圖中uin和uex分別為PI調(diào)節(jié)器輸入電壓和輸出電壓,在圖1中,由于運算放大器的反相作用,uin和uex的極性是相反的(圖中所示的極性表明調(diào)節(jié)器的輸入信號和輸出信號是反相的)。電阻Rbal為平衡電阻,接在運算放大器的同相輸入端,通常其值的大小為運算放大器反相輸入端各電阻的并聯(lián)值。依據(jù)運算放大器的輸入-輸出關(guān)系,可以得到
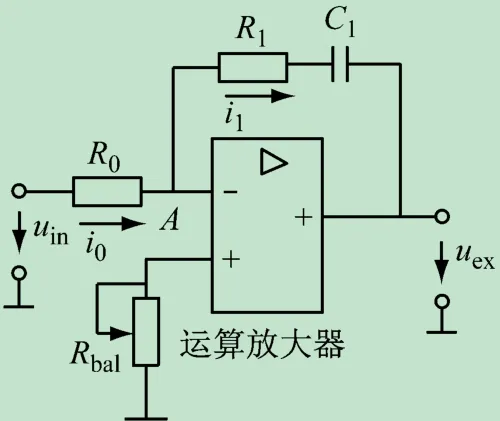
圖1 PI調(diào)節(jié)器電路原理圖
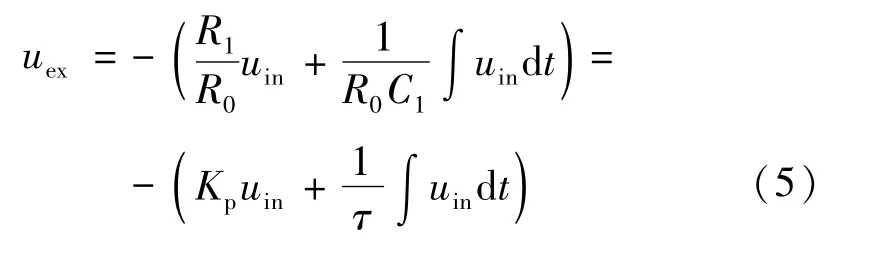
式中:Kp=R1/R0;τ=R0C1。
在零初始狀態(tài)和方波輸入電壓uin下,PI調(diào)節(jié)器的輸出電壓uex的時間特性如圖2所示。當(dāng)t=0時突加輸入電壓uin,由于比例部分的作用,輸出量uex立即響應(yīng),馬上跳變?yōu)閡ex(t)=-Kpuin,實現(xiàn)了系統(tǒng)的快速響應(yīng);之后uex(t)按照積分規(guī)律增長,uex=-[Kpuin+(uin/τ)t],在t=t1時,輸入電壓uin突變?yōu)榱悖瑄in=0,uex=(uin/τ)t1,PI調(diào)節(jié)器的積分調(diào)節(jié)作用使其后級的電力電子變換器輸出穩(wěn)態(tài)電壓,足以克服系統(tǒng)的負載電流壓降[2-4],實現(xiàn)系統(tǒng)的穩(wěn)態(tài)轉(zhuǎn)速(或者其他變量)無靜差調(diào)節(jié)。
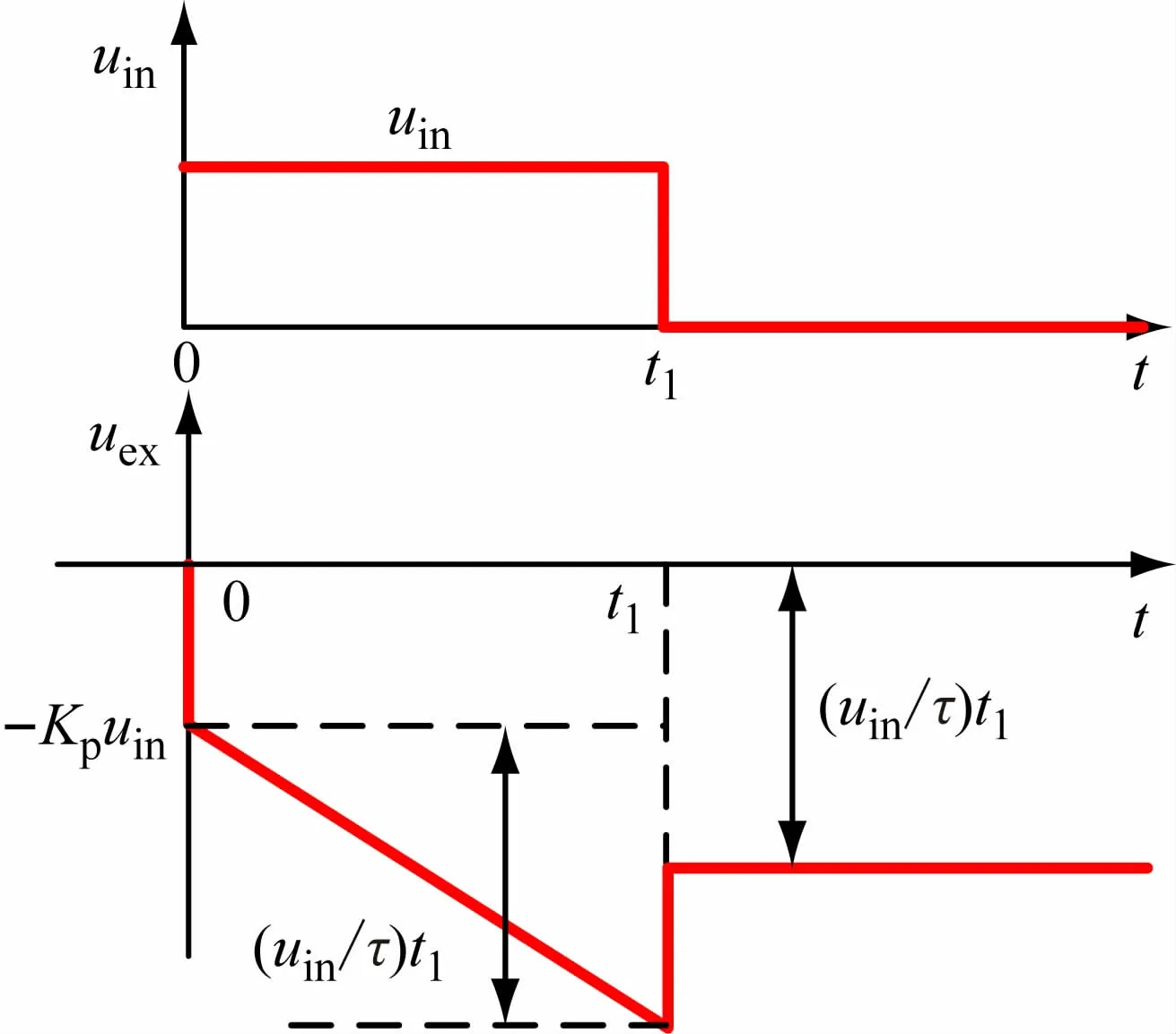
圖2 PI調(diào)節(jié)器的輸入-輸出特性
結(jié)合圖1,從圖2的特性圖上也可以看出PI作用的物理意義。由于系統(tǒng)處于零初始狀態(tài),突加輸入電壓uin時,對于電容C1來說,由于電容兩端的電壓不能突變,相當(dāng)于兩端瞬時短路,此時PI調(diào)節(jié)器相當(dāng)于一個單純的反相比例放大器,所以輸出電壓會立即跳變到uex=-Kpuin,保證了系統(tǒng)的快速響應(yīng)。此后,電容C1被充電,輸出電壓uex開始積分,其數(shù)值線性增長。由圖2可見,如果輸入電壓uin一直存在或者輸入電壓uin的值比較大(該值決定了積分的斜率),電容C1就不斷被充電,不斷進行積分,直到輸出電壓uex達到運算放大器的限幅值-uexm為止,此時就稱運算放大器飽和。為保證線性放大作用并保護系統(tǒng)各環(huán)節(jié),對具有積分作用的運算放大器設(shè)置輸出電壓限幅是非常必要的。在實際的轉(zhuǎn)速閉環(huán)控制系統(tǒng)中,當(dāng)轉(zhuǎn)速上升到給定值時,PI調(diào)節(jié)器的輸入電壓uin=0,此時積分過程也就停止了。對于圖2而言,在PI調(diào)節(jié)器的調(diào)節(jié)過程中,如果不考慮運算放大的飽和作用,在t=t1時,輸入電壓uin=0,此時PI調(diào)節(jié)器失去比例放大作用,因此系統(tǒng)的輸出電壓會有所降落,系統(tǒng)成為積分器維持電容C1上的電壓輸出,亦即積分電壓值輸出uex=-(uin/τ)t1。
如果采用數(shù)字控制,可將式(1)或者式(5)的時域方程離散化為差分方程,用數(shù)字PI算法實現(xiàn),但是其物理意義還是一樣的,在此就不再贅述。
由此可見,PI調(diào)節(jié)器綜合了比例控制和積分控制兩種控制規(guī)律的優(yōu)點,揚長避短,互相補充,可以實現(xiàn)系統(tǒng)的動態(tài)快速控制和穩(wěn)態(tài)無靜差控制。在閉環(huán)調(diào)速控制系統(tǒng)中,負載的擾動會引起輸入偏差電壓Δun的變化,圖3給出了PI調(diào)節(jié)器的輸入輸出的動態(tài)過程,不妨假設(shè)閉環(huán)調(diào)速系統(tǒng)的輸入偏差電壓Δun的波形如圖3所示,采用PI調(diào)節(jié)器的輸出電壓uc的波形③由兩部分疊加而成,即與輸入偏差電壓Δun成正比的波形①,輸入偏差電壓Δun的積分波形②,由此可見,控制電壓uc既具有快速響應(yīng)的性能,又足以消除系統(tǒng)的靜差[2],除此之外,PI調(diào)節(jié)器還是提高系統(tǒng)穩(wěn)定性的校正裝置,因而PI調(diào)節(jié)器在調(diào)速系統(tǒng)[3-4,14]和其他控制系統(tǒng)中得到了極為廣泛的應(yīng)用。
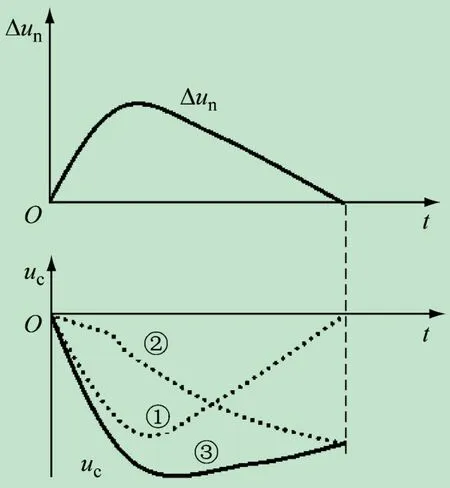
圖3 閉環(huán)系統(tǒng)中PI調(diào)節(jié)器的輸入和輸出動態(tài)調(diào)節(jié)過程
2 PI調(diào)節(jié)器的Simulink建模與性能研究
在自動控制系統(tǒng)中,PI調(diào)節(jié)器的傳遞函數(shù)既可以用Matlab語句表達,也可以用Simulink的傳遞函數(shù)模塊和比例模塊、積分模塊表達,使用Simulink模塊不僅方便,而且可以反映調(diào)節(jié)器的輸出限幅作用,但按照式(3)用Simulink傳遞函數(shù)模塊和按照式(4)用比例積分模塊建立的仿真模型的性能和效果是不一樣的,下邊分別進行研究。
2.1 PI調(diào)節(jié)器傳遞函數(shù)模型
依據(jù)式(3)用Simulink傳遞函數(shù)模塊建立的PI調(diào)節(jié)器的仿真模型如圖4所示。
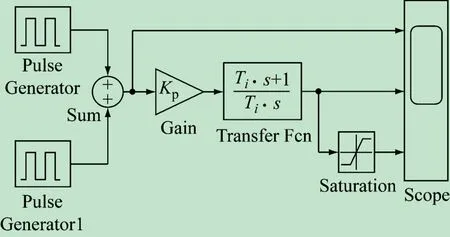
圖4 PI調(diào)節(jié)器傳遞函數(shù)Simulink仿真模型
模型中用放大模塊Gain和傳遞函數(shù)模塊Transfer Fcn組成PI調(diào)節(jié)器的傳遞函數(shù)形式[11-12]。放大模塊Gain的放大倍數(shù)為Kp,利用傳遞函數(shù)模塊Transfer Fcn來設(shè)置PI調(diào)節(jié)器的積分時間常數(shù),兩個脈沖模塊Pulse Generator和Pulse Generator1經(jīng)過信號求和模塊Sum產(chǎn)生脈沖寬度可以調(diào)整的輸入信號,作為PI調(diào)節(jié)器的輸入源,以此觀察PI調(diào)節(jié)器在偏差輸入信號下的動態(tài)響應(yīng)。Saturation模塊用來設(shè)置限制PI調(diào)節(jié)器的輸出電壓幅值,用示波器Scope觀察PI調(diào)節(jié)器在有、無限幅作用情況下的輸出電壓的波形,并分別與PI調(diào)節(jié)器的輸入信號進行比較。
系統(tǒng)的仿真參數(shù)見表1,選擇ode45算法,仿真時間設(shè)為2個周期(6 s),仿真結(jié)果如圖5所示。

表1 PI調(diào)節(jié)器傳遞函數(shù)模型的仿真參數(shù)
圖5(a)為PI調(diào)節(jié)器的輸入信號波形,圖5(b)為PI調(diào)節(jié)器無限幅的輸出波形,圖5(c)為PI調(diào)節(jié)器經(jīng)過限幅后的輸出波形,由圖5(a)、(b)可見,在輸入信號脈沖值為“-1 V”的時間段內(nèi)(t=0~0.6 s),由于比例放大系數(shù)Kp=2,因此PI調(diào)節(jié)器的輸出在t=0時從2 V開始在積分作用下線性增長;在輸入信號脈沖值為“0 V”的時間段內(nèi)(t=0.6~1.5 s),PI調(diào)節(jié)器的輸出維持t=0.6 s的輸出值20 V不變;在輸入信號脈沖值為“1 V”的時間段內(nèi)(t=1.5~2.1 s),由于輸入信號變負,積分器開始反相積分,PI調(diào)節(jié)器的輸出值開始降低。在t=2.1 s時,輸入信號再次變?yōu)?,此時PI調(diào)節(jié)器輸出維持不變。由圖5(a)、(c)可見,如果PI調(diào)節(jié)器的輸出增加了限幅環(huán)節(jié),那么PI調(diào)節(jié)器的輸出幅值就會被限制在設(shè)定值±10 V之間。
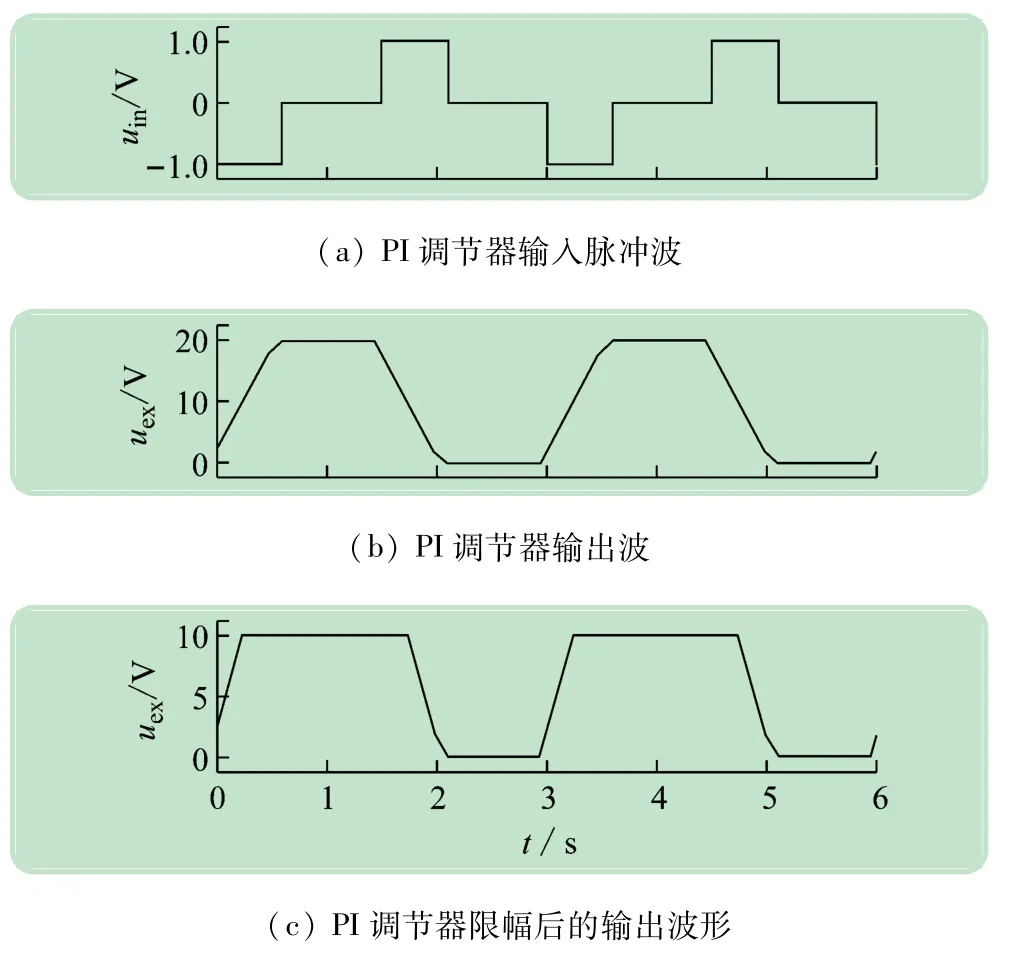
圖5 PI調(diào)節(jié)器傳遞函數(shù)模型的仿真波形
由圖5可知,PI調(diào)節(jié)器在正或者負的輸入信號作用下,其輸出信號也隨之增加或者減少;當(dāng)輸入信號變?yōu)? V時,PI調(diào)節(jié)器能維持前一時刻輸入變?yōu)? V時的輸出值,該輸出電壓值與積分的時間(脈沖寬度)密切相關(guān)。一般情況下,自動控制系統(tǒng)都是采用PI調(diào)節(jié)器來消除系統(tǒng)的誤差,在系統(tǒng)輸出產(chǎn)生誤差時,PI調(diào)節(jié)器能立即產(chǎn)生可消除誤差的控制信號。從圖5所示的輸出波形上也可以看出,在系統(tǒng)存在誤差時,也就是PI調(diào)節(jié)器存在輸入電壓信號時,PI調(diào)節(jié)器能夠迅速按照積分規(guī)律產(chǎn)生輸出控制信號,在這里,PI調(diào)節(jié)器的積分時間常數(shù)Ti影響輸出控制信號上升或者下降的斜率(積分曲線的斜率),而且能夠在誤差為0(輸入電壓為0)時,保持之前PI調(diào)節(jié)器的輸出狀態(tài),PI調(diào)節(jié)器的比例系數(shù)Kp抬高了PI調(diào)節(jié)器的輸出信號值,起著迅速加快調(diào)節(jié)的作用。
對于圖4所示的Simulink仿真模型而言,PI調(diào)節(jié)器的輸出信號是隨著積分時間而增長的,積分時間越長,PI調(diào)節(jié)器的輸出值也就越高,這與實際的PI調(diào)節(jié)器的工作情況是不相符的。這也是許多研究者建模時所容易忽略的一個問題,導(dǎo)致在采用該模型進行建模仿真時,得不出正確的結(jié)果。對于實際的PI調(diào)節(jié)器而言,不論是模擬的PI調(diào)節(jié)器,還是數(shù)字式的PI調(diào)節(jié)器,都會對積分環(huán)節(jié)加上幅值限制環(huán)節(jié)[8-10],使其輸出不能隨時間無限制的增長。從圖5的仿真波形中可以看出,模型中的限幅模塊限制了調(diào)節(jié)器的輸出,但是在輸出限幅時,調(diào)節(jié)器的積分作用還在繼續(xù)起作用,從而使得系統(tǒng)在出現(xiàn)負偏差信號的時候,限幅輸出信號的下降時間要滯后于負偏差信號。從圖5(b)、(c)可以看出,在t=1.5 s時,無限幅PI調(diào)節(jié)器的輸出信號值從20 V開始下降,但是有限幅環(huán)節(jié)的PI調(diào)節(jié)器輸出信號卻是在t=1.75 s時開始從10 V下降,這也是容易造成自動控制系統(tǒng)超調(diào)的原因[15-16]。
2.2 帶積分限幅的PI調(diào)節(jié)器模型
帶積分限幅的實用PI調(diào)節(jié)器仿真模型按照式(4)在Simulink中搭建,式中的積分環(huán)節(jié)使用Integrator模塊來實現(xiàn)[6],該Integrator模塊可以限制積分輸出的最大值,用Integrator模塊搭建的PI調(diào)節(jié)器的模型如圖6所示。圖中,可由增益模塊Gain1設(shè)置PI調(diào)節(jié)器的比例放大系數(shù)Kp,增益模塊Gain3用來設(shè)置PI調(diào)節(jié)器的積分時間系數(shù)Ki(Ki=1/Ti),積分器Integrator模塊的限幅值可以設(shè)置成運算放大器的飽和輸出值,在仿真模型中設(shè)置成了±15 V,對于其他環(huán)節(jié)的參數(shù),和前面圖4的參數(shù)基本相同,對該模型進行仿真,所得到的帶積分限幅的PI調(diào)節(jié)器的仿真波形如圖7所示。圖7(a)是PI調(diào)節(jié)器的輸入電壓仿真波形,圖7(b)是經(jīng)過比例放大2倍后的運算放大器輸出波形,圖7(c)是積分器Integrator模塊飽和限幅之后的仿真波形,圖7(d)是限幅之后的PI調(diào)節(jié)器的輸出仿真波形。由圖7(c)、(d)中可見,由于積分器設(shè)置了±15 V限幅值,PI調(diào)節(jié)器設(shè)置了±10 V限幅值,PI調(diào)節(jié)器的輸出限幅值小于積分器的輸出限幅值,因此,輸入電壓信號在1.5 s由0 V變成負值之時,積分調(diào)節(jié)器的輸出值立即開始從正的限幅值+15 V下降,但對于PI調(diào)節(jié)器來說,其輸出值卻是在1.6 s的時候開始從正的限幅值+10 V下降,這兩個仿真波形之間存在著0.1 s的時間延時,這相當(dāng)于由運算放大器組成的帶輸出限幅環(huán)節(jié)的PI調(diào)節(jié)器的退飽和延時。如果將積分調(diào)節(jié)器的限幅值和PI調(diào)節(jié)器的輸出限幅值都設(shè)置成+10 V,那么圖7(c)、(d)的仿真波形將會完全一致,不會存在時間延遲。所以,在數(shù)字PI調(diào)節(jié)器中,為了減小閉環(huán)調(diào)節(jié)系統(tǒng)的退飽和超調(diào)量,通常取積分器的限幅值和PI調(diào)節(jié)器的輸出限幅值相同。
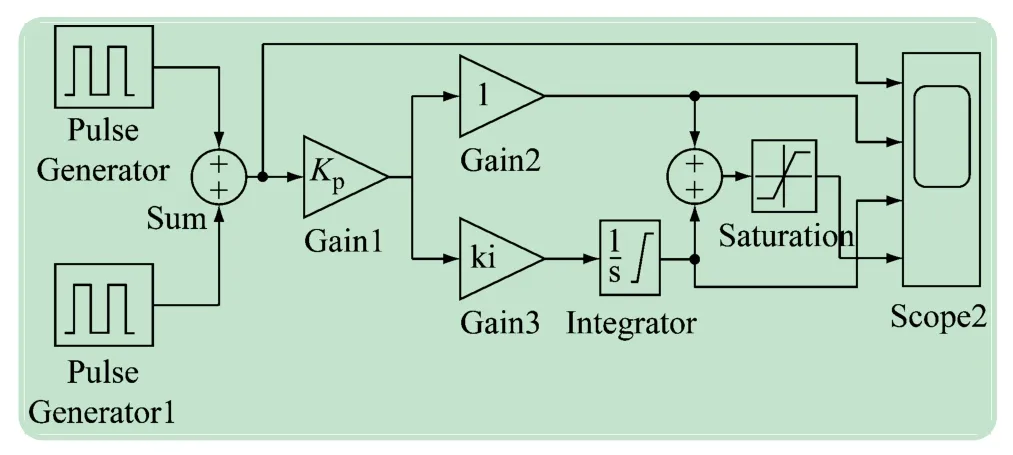
圖6 帶積分限幅的實用PI調(diào)節(jié)器仿真模型
比較圖5和圖7可知,在輸入脈沖信號完全相同的情況下,對于帶積分限幅的PI調(diào)節(jié)器模型和無積分限幅作用的PI調(diào)節(jié)器傳遞函數(shù)模型來說,其輸出是不同的,對系統(tǒng)的影響也是不一樣的。尤其是對于自動控制系統(tǒng)來說,在進行系統(tǒng)建模的時候,PI調(diào)節(jié)器采用帶積分限幅的PI調(diào)節(jié)器模型是非常重要的。為了使用上的方便,可以將該模型封裝為一個PI控制器子系統(tǒng),使用的時候直接作為一個分支模塊使用就行了,只需要修改其相應(yīng)的Kp、Ki、積分限幅值、PI調(diào)節(jié)器限幅值等幾個參數(shù)即可。這樣在將其應(yīng)用到規(guī)模較大的復(fù)雜系統(tǒng)時會使得模型變得更加簡潔。
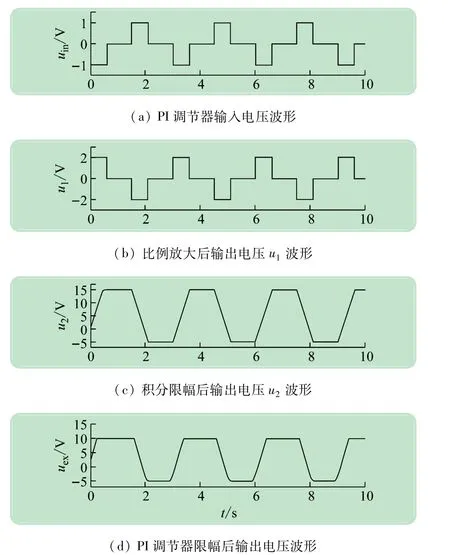
圖7 實用PI調(diào)節(jié)器模型的仿真波形
3 PI調(diào)節(jié)器輸入輸出特性的驗證
采用帶積分限幅的PI調(diào)節(jié)器模型也可以對PI調(diào)節(jié)器的輸入-輸出特性進行驗證,調(diào)整兩個Pulse脈沖,可以將PI調(diào)節(jié)器的輸入脈沖信號調(diào)整為正的方波電壓信號,如圖8(a)所示,在整個動態(tài)調(diào)節(jié)過程中,設(shè)置PI調(diào)節(jié)器一直處于不飽和狀態(tài),由圖8(c)可見,在0~4 s時間段內(nèi),積分器從0開始反相線性積分,到4 s時,輸入脈沖信號變?yōu)?,積分器停止積分,并維持在-3.2 V。從圖8(d)可以看出,t=0 s時,PI調(diào)節(jié)器的輸出就變?yōu)? V,也就是說此時只有比例部分起快速調(diào)節(jié)作用,隨后PI調(diào)節(jié)器的輸出反相線性上升,直至t=4 s時,輸出電壓信號達到-7.08 V。t=4 s時,PI調(diào)節(jié)器的輸入電壓信號變?yōu)? V,對于比例放大部分,已經(jīng)失去了放大作用,此時PI調(diào)節(jié)器靠積分器的輸出來維持系統(tǒng)需要的穩(wěn)態(tài)輸出信號,因此,在t=4 s時,PI調(diào)節(jié)器的輸出信號由-7.08 V升至-3.2 V。從而也驗證了PI調(diào)節(jié)器在方波輸入電壓信號下的輸入-輸出特性。
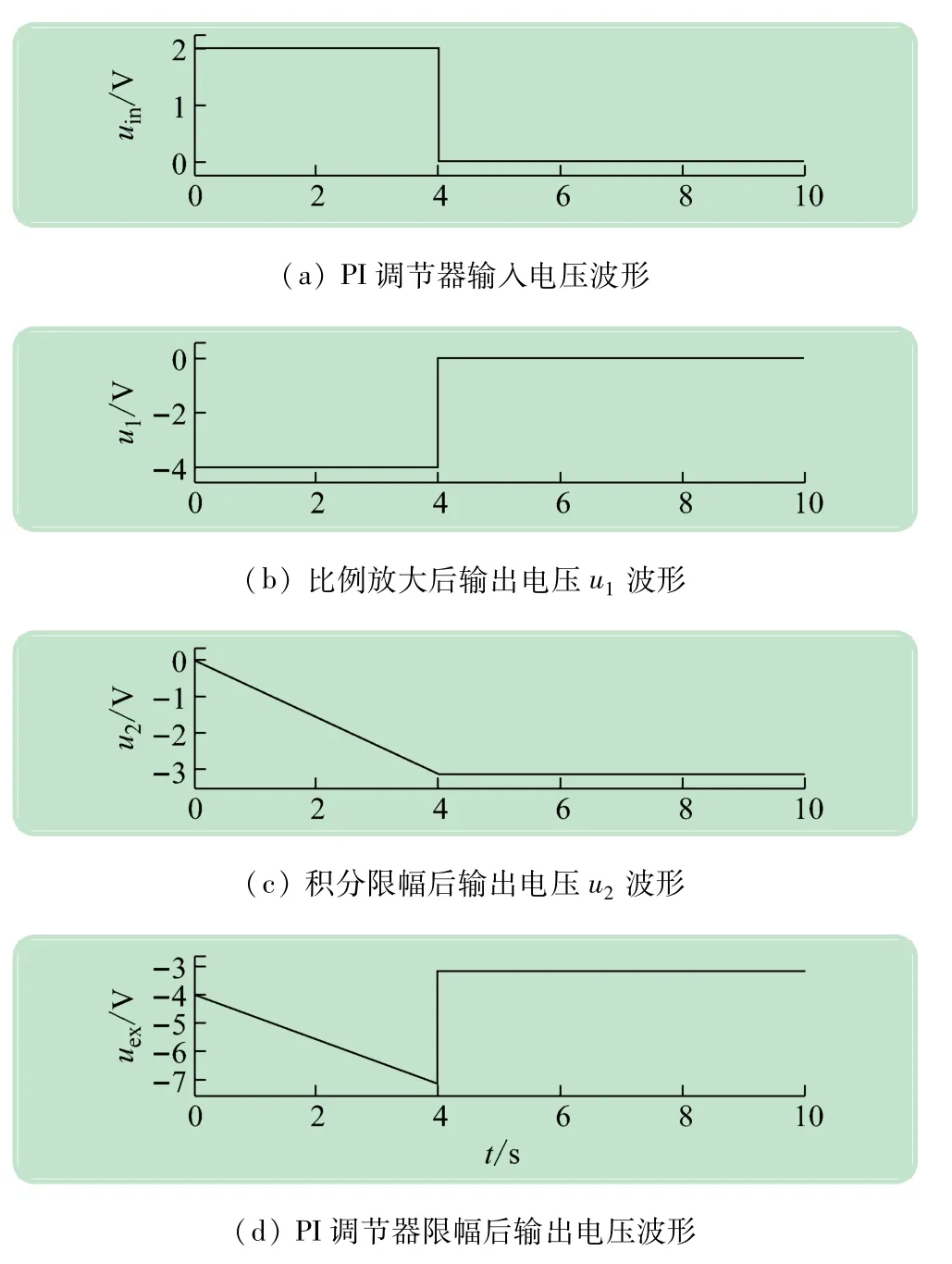
圖8 方波電壓輸入信號下PI調(diào)節(jié)器的輸入輸出特性仿真
4 結(jié) 語
PI調(diào)節(jié)器是自動控制系統(tǒng)設(shè)計時的一個重要環(huán)節(jié),尤其是在建模仿真分析的時候,PI調(diào)節(jié)器仿真模型構(gòu)建的好壞將會直接影響自動控制系統(tǒng)的性能,因此建立合理的PI調(diào)節(jié)的仿真模型至關(guān)重要。本文在分析PI調(diào)節(jié)器的組成及輸入輸出特性的基礎(chǔ)上,研究了其Simulink仿真模型,得出以下結(jié)論。
(1)PI調(diào)節(jié)器可以用式(3)、(4)兩種不同的傳遞函數(shù)表示,可以依據(jù)這兩個公式分別建立PI調(diào)節(jié)器的仿真模型。
(2)依據(jù)式(3),利用Simulink的傳遞函數(shù)模塊建立的PI調(diào)節(jié)器仿真模型,無積分限幅作用,只能對整個PI調(diào)節(jié)器的輸出進行限幅,使得系統(tǒng)在出現(xiàn)負偏差信號的時候,限幅輸出信號的下降時間要滯后于負偏差信號,容易導(dǎo)致自動控制系統(tǒng)超調(diào),與實際PI調(diào)節(jié)器的工作狀態(tài)存在一定的差異。因此不建議在構(gòu)建自動控制系統(tǒng)仿真模型時采用該PI調(diào)節(jié)器仿真模型。
(3)按照式(4),利用Simulink的比例和積分模塊建立的帶積分限幅的PI調(diào)節(jié)器仿真模型,與實際PI調(diào)節(jié)器性能相符,可以靈活的設(shè)置積分器和PI調(diào)節(jié)器的限幅值,能夠有效減小閉環(huán)調(diào)節(jié)系統(tǒng)的退飽和超調(diào)量。為了使用上的方便,可以將其封裝為一個子系統(tǒng)進行使用。
(4)利用帶積分限幅的PI調(diào)節(jié)器仿真模型可以有效的驗證PI調(diào)節(jié)器在方波輸入信號作用下的輸入輸出特性。

