希帕索斯悖論與無理數

林革

說到希帕索斯悖論，首先要提到的是畢達哥拉斯學派和畢達哥拉斯定理.

畢達哥拉斯是一位與孔子、釋迦牟尼幾乎同時代的古希臘著名數學家和哲學家. 他創辦了一個著名的學派——畢達哥拉斯學派，其宗旨是“萬物皆數”.

畢達哥拉斯學派認為：世界上的萬事萬物都可以用數來表示，一切事物都由數構成. 無論什么事物，大到天體，小到塵埃，都有一定的長短、高低、大小、輕重等數量，沒有數量的事物是不存在的. 總之，一切事物都必須而且只能通過數得到解釋，宇宙的本質和規律就是數的和諧，也就是說，宇宙間的一切現象都能歸結為整數或整數之比. 顯然“萬物皆數”中的數就是有理數.

畢達哥拉斯定理就是著名的勾股定理，即直角三角形斜邊的平方等于兩直角邊平方之和. 據說畢達哥拉斯發現這個定理有一段有趣的淵源.

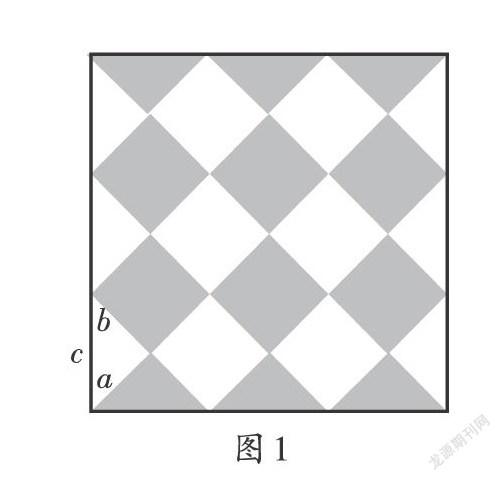
有一次，畢達哥拉斯被邀請到朋友家做客，客人們高談闊論，他卻一言不發，靜靜地坐在那里. 他本來就是一個沉默寡言、不愛湊熱鬧的人，平時除了思考數學問題和別人溝通交談外，沒有任何別的事情能讓他多費口舌. 畢達哥拉斯一直低頭看地上鋪的花磚（花磚形狀如圖1），屋里沒人感到奇怪.

花磚上的圖形有正方形和三角形，黑白相間且有規律地排列著，這好像沒什么特別的，可畢達哥拉斯竟被這個司空見慣的圖案吸引住了. 他幾乎忘記了自己是來做客的，竟彎下腰去，在靠邊的花磚上算了起來.

畢達哥拉斯在直角三角形的一條直角邊上寫上a，另一條直角邊上寫上b，在斜邊上寫上c（如圖1）. 以a為邊的正方形面積a2恰好等于兩個灰色三角形面積的和，以b為邊的正方形面積b2恰好等于兩個白色三角形面積的和，以c為邊的正方形面積c2恰好等于兩個灰色三角形與兩個白色三角形面積的和，即c2 = a2 + b2. 由此，畢達哥拉斯得出結論：以c為邊的大正方形面積等于以a或b為邊的兩個小正方形面積的和.

畢達哥拉斯和他的門徒在給出這條定理的證明后欣喜若狂，宰了100頭牛，舉辦了盛大的“百牛宴”以示慶賀. 因此，勾股定理也被稱為“百牛定理”.

不過，具有諷刺意味的是，畢達哥拉斯定理的發現和證明導致畢達哥拉斯學派的宗旨被動搖了.

畢達哥拉斯學派中的一個青年弟子希帕索斯，在研究正方形的對角線時發現，這條對角線既不能用整數表示，也不能用整數之比（分數）表示. 因為，如果能用整數或整數之比表示，則必然帶來不可克服的矛盾. 具體推導如下：

假設正方形的邊長為1，如圖2，

則根據勾股定理可知斜邊w2 = 12 + 12 = 2，這個w一定不是整數，

因為12 = 1，22 = 4，

而12 < w2 < 22，

又因為1和2是兩個連續的自然數，

所以w只能是夾在1和2之間的分數.

假設這個分數為[mn]，

必須說明該分數是既約分數（m，n已經約去了所有的公因數），

可得結論：m，n之中至少有一個奇數（若兩者都是偶數，則存在公因數2，這與前提假設矛盾）.

∵[m2n2] = 2， ∴m2 = 2n2.

又∵2n2為偶數，∴ m2為偶數，

如果m為奇數，那么m可以表示成2p + 1，

則m2 = （2p + 1）2=4（p2 + p） + 1也是奇數，這與上面得到的m2為偶數矛盾.

∴m必為偶數.

又∵m，n二者中至少有一個奇數，m必為偶數，

∴n必為奇數.

m為偶數，可設 m=2p，即m2=4p2=2n2，得n2=2p2，

也就是說n2為偶數，則n必為偶數. 這又與上面得到的n必為奇數矛盾.

不難看出，同一個數n既是奇數又是偶數.

但是我們都知道，一個數要么是奇數，要么是偶數，不能既是奇數又是偶數.

因此，以上循環必然產生矛盾，人們把這種循環稱為希帕索斯悖論.

推導過程之所以出現矛盾的結論，無外乎以下兩種原因：一種是前提錯誤，一種是推導過程錯誤. 以上的推導過程中使用了兩個前提：一個是畢達哥拉斯學派“一切現象可歸結為整數或整數之比”的信念，另一個就是畢達哥拉斯定理. 然而，由二者都推出了矛盾.

顯然，上述推導過程毫無差錯，那么問題只能出在前提上. 畢達哥拉斯定理是已證明為正確的定律，這樣只能說明畢達哥拉斯學派的信念不成立. 希帕索斯悖論的發現如同一聲晴天霹靂，動搖了畢達哥拉斯學派整個信念大廈的基礎，引起了學派極大的恐慌，以至于希帕索斯最終為了真理付出了生命的代價.

然而“青山遮不住，畢竟東流去”，人們又發現了其他不能用整數或整數之比表示的數，如[3]，[5]，[7]，[π]等，如今這些無理數已經被大眾普遍接受.

雖然希帕索斯被拋到大海里淹死，但希帕索斯悖論是淹不死的. 這些事實像潮水一樣猛烈地沖擊著傳統觀念，促使人們重新審視“一切數都是整數或整數比”的有理數理論，這就是歷史上的第一次數學危機. 當然，從本質上嚴格來說，這種危機并不是數學本身的危機，而是畢達哥拉斯學派“萬物皆數”（整數或整數之比）信念的危機.

（作者單位：揚州職業大學）