小學3～5年級學生數學學習動機調查
——以蒲江縣大興九年制義務學校為例

吳謙謙，廖全明，于敏章

（成都師范學院心理學院，四川成都 611130）

個體在生活、學習、工作等各個方面都離不開動機。伍德沃斯認為“動機是激發外在行為的內部動力”；在《心理學大辭典中》中，動機是“能引起一個人的活動，并將該活動導向某一目標，以滿足個體某種需要的念頭、愿望、理想等。”

有學者將動機分為外部動機（Lee 1991；Spaulding，1992），內部動機（Pintrich&Schunk，2002），但不管是外部動機還是內部動機，其實都是相輔相成的，更好的促使個體朝著目標而前行。

學者奧蘇貝爾發展出學業成就動機的理論，并將其詳細劃分為認知內驅力、自我提升內驅力、附屬內驅力。劉秀君認為“數學學習動機是指個人因為興趣、發展需求或某種心理需要產生的學好數學的欲望與動力”[1]。因此激發數學學習動機對小學生學習數學至關重要。林慶波認為“有效激發小學生數學學習的動機，提高學生在數學學習活動中的主動性，是提升現有小學數學教學水平的關鍵所在”[2]。在實際教學中，數學學習動機的引發主要源于學生內部心理特征以及與其所處環境之間的交互作用，教師應該使學生學習數學的外部動機逐漸轉化為內部動機，同時也要通過外部動機來持續激發內部動機。

目前，對小學生的數學學習動機研究中以問卷調查為主，測驗工具有學習動機診斷測驗（MAAT)、學習動機問卷（Nagy 1996）以及研究者自編的問卷等。當然，學習動機成分由問卷的不同，分類也有不同。

此外，學者孔企平的研究表明“數學學習動機對學生學業成績有顯著的預測作用，即具有高數學動機的學生在數學學習方面都表現較好，在學習的主動性方面也表現得更積極[3]。”因此，該文通過研究小學3～5年級的學生在學習數學上的動機內外部因素，并驗證數學學習動機高低與數學成績之間的關系，有助于激發學生學習數學興趣，以及提高教師教學水平提供一定的參考基礎。

1 研究假設

該文通過研究3～5年級小學生的數學學習動機，想了解以下3 點。

（1）小學3～5年級學生數學學習動機在性別、年級上是否存在顯著差異。

（2）小學3～5年級學生學習動機內外部因素是否對數學成績存在中介作用。

（3）小學3～5年級學生數學學習動機的得分對數學成績的高低產生的影響如何。

該研究以小學3～5年級為調查對象，以問卷調查的形式，對其數學學習動機特點進行探索分析。

2 研究方法

2.1 研究對象

該文采取方便抽樣，在成都市蒲江縣大興九年制義務學校，在3年級、4年級和5年級里各自選取了一個班來進行問卷調查，共發放問卷109 份，現場收取109 份，剔除無效問卷（如信息漏填、亂填的），共獲得有效問卷103 份，回收率為100%，有效率為94.5%,具體情況見表1。

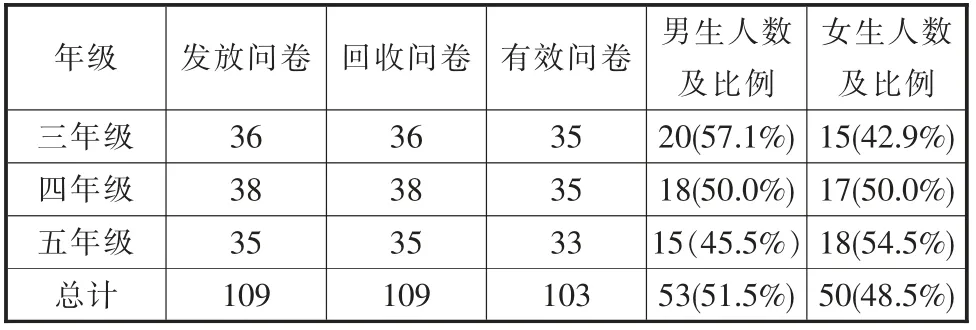
表1 被試情況

2.2 問卷分析

該研究所使用的問卷，參考的是學者張紅芳的《小學生數學學習動機調查問卷》，共有25 題，共分為兩個一級維度和六個二級維度，如表2 所示。

《小學生數學學習動機調查問卷》的信度——克倫巴赫系數為0.705，效度為0.617，表示尚可。該次研究所采用的問卷信度結果見表3，問卷效度結果見表4。

表3 調查問卷的信度分析（n=103）

表4 調查問卷的效度分析（n=103）

內部一致性信度是最常用的表示問卷信度的方法，用Cronbach's Alpha 系數(即克倫巴赫系數)來表示，克倫巴赫系數在0.6 以上為可用，在0.7 以上為良好，在0.8 以上為較好，在0.9 以上為最好。

該問卷選用264 名樣本進行信效度檢驗。該研究所采用的問卷信度分析結果，如表3 所示，從中可以看出，克倫巴赫系數為0.668，顯示該問卷可用于施測。

該問卷進行了KMO 和Bartlett 球形檢驗，結果如表4 所示，Bartlett 球形檢驗的近似χ2值為629.270，P 值為0.000，KMO 值為0.664，大于0.6，表示效度尚可。

2.3 研究結果

F1～F6 維度上各個年級的均值與標準差如表5所示。

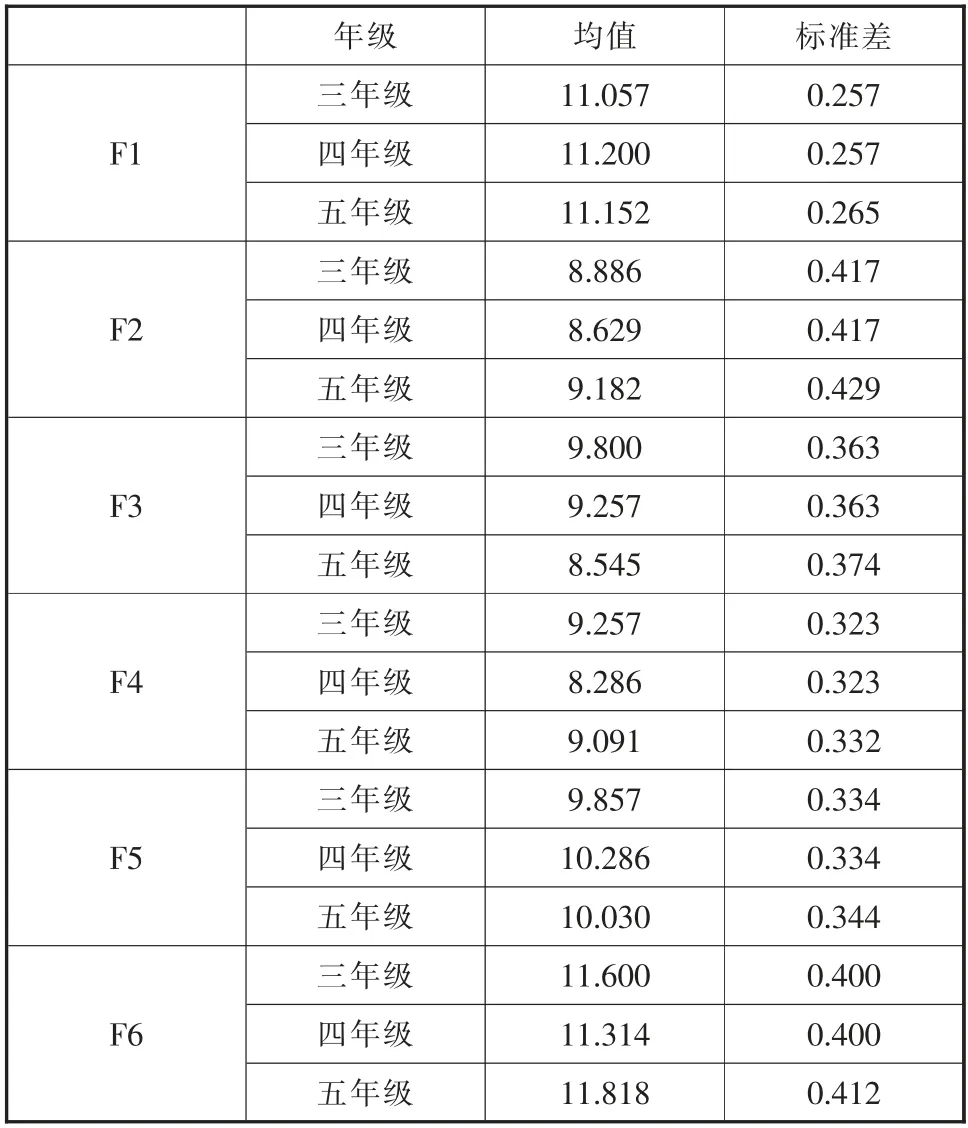
表5 描述統計分析（n=103）

為了檢驗性別在各個維度上的得分是否存在顯著差異，通過單因素檢驗，結果如表6 所示。

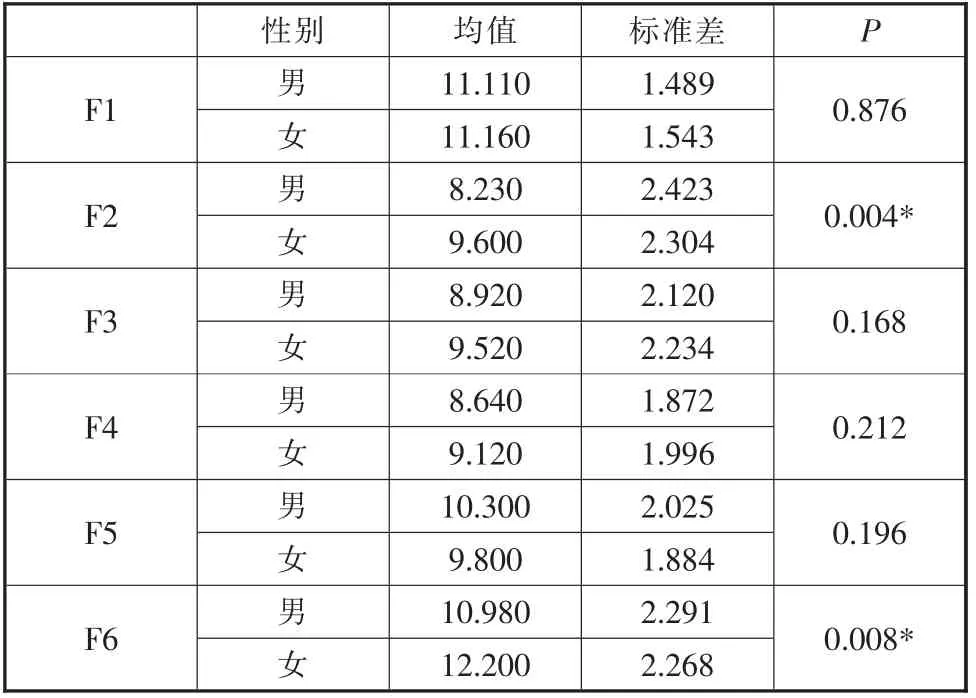
表6 性別的單因素檢驗（n=103）

由表6 可以看出，在掌握—回避定向，以及避免失敗動機上，男女存在顯著差異。即女生比男生更加傾向去避免不能理解或不能掌握的數學學習任務，且女生更加傾向避免失敗，這一點與張紅芳學者的研究結果一致[4]。

相關性分析，通過期中成績與各個因素進行相關性分析，結果如表7 所示。

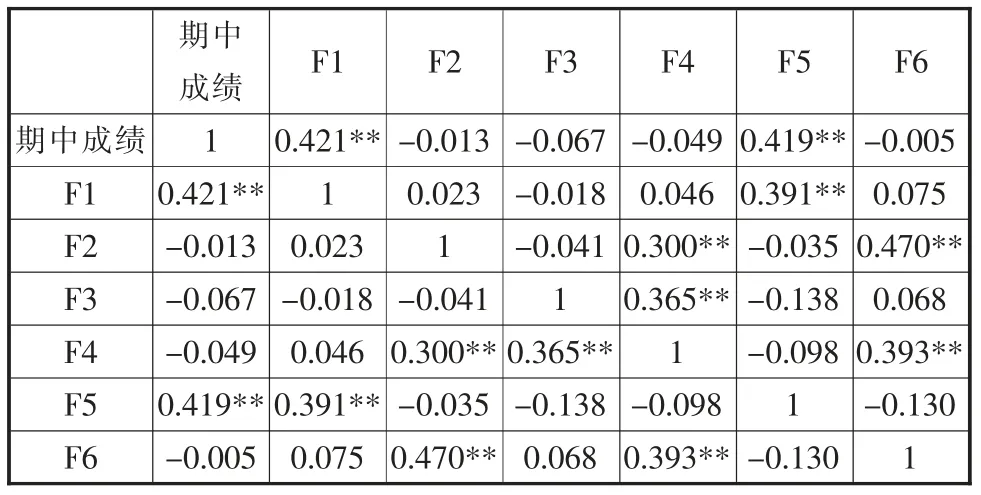
表7 相關性分析（n=103）

由表7 可以看出，期中成績與F1（掌握—接近定向）存在顯著正相關；期中成績和F5（追求成功動機）存在顯著正相關；F1（掌握—接近定向）和F5（追求成功動機）存在顯著正相關；F2（掌握—回避定向）和F4（成績—回避定向）存在顯著正相關；F2（掌握—回避定向）和F6（避免失敗動機）存在顯著正相關；F4（成績—回避定向）和F6（避免失敗動機）存在顯著正相關。

為了進一步了解小學3～5年級學生的期中成績、F1（掌握—接近定向）、F5（追求成功動機）的關系，該研究的自變量是F1（掌握—接近定向）、F5（追求成功動機），因變量是期中成績，對其進行多元線性的回歸進入分析，最終得到影響小學3～5年級學生的期中成績最大的因素是F1（掌握—接近定向），結果如表8 所示。

表8 F1、F5 和期中成績的回歸分析

由模型R2判定系數可知，掌握—接近定向這個因素總共可解釋期中成績的17.7%，其標準化回歸方程為：期中成績=13.826+0.421*（掌握—接近定向）。

根據Kenny&Baron（1986）認為中介效應的檢驗效果同時滿足以下條件：X 顯著影響Y；X 顯著影響M；M 顯著影響Y；M 與X 都同時進入回歸方程時，若X 對Y 的影響系數顯著下降，說明M 起到部分中介作用[5]。通過上圖的回歸分析，發現當追求成功動機這個因素和掌握—接近定向這個因素同時進入回歸方程時，掌握—接近定向對期中成績的影響系數下降了，由原來的0.421 下降到0.304。

因此我們推測，追求成功動機這個因素在掌握—接近定向和期中成績之前起到一個部分中介作用，并通過Process v3.4 進行驗證，得到的結果如表9 和表10 所示。

表9 中介作用的模型檢驗

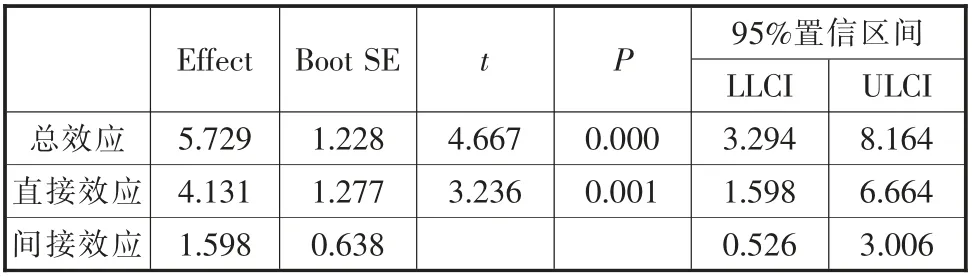
表10 追求成功動機的中介效應檢驗

通過以上中介作用的模型檢驗和追求成功動機的中介效應檢驗，追求成功動機在掌握—接近定向和期中成績中起部分中介作用，繪制關系如圖1所示。

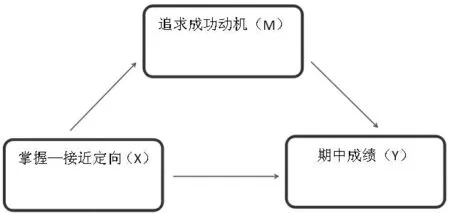
圖1 期中成績與追求成功動機和掌握—接近定向的關系

因此，通過以上的數據分析，我們得出了影響小學3～5年級學生的期中成績最重要的兩個因素是F1（掌握—接近定向）和F5（追求成功動機），F1 除了能直接影響期中成績外，還能通過影響F5 來間接影響期中成績，這就是追求成功動機的中介效應。

最后，我們將各個因素所得分相加，就得到了學習動機的總得分，將總得分與期末成績進行相關分析，結果如表11 所示。

表11 期中成績與總動機得分（n=103）

由于在期中成績得分上，有3 位學生的期中成績得分低于15 分（分別為4 分、11 分、13 分），因此我們將這3 位學生的數據進行剔除，得出的結果如表12 所示。

表12 期中成績與總動機得分（n=100）

如表12 所示，sig=0.04＜0.05，即期中成績與動機得分在0.05 的水平上存在顯著相關，因此我們對期中成績和總動機得分進行一個回歸分析，如表13所示。

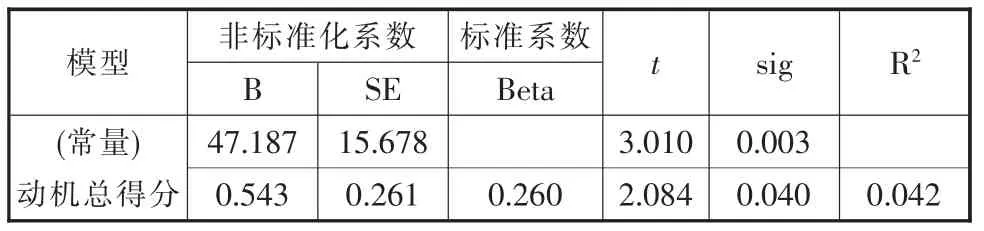
表13 期中成績與總動機得分回歸分析（n=100）

根據表13 所示，其標準化回歸方程為：期中成績=47.187+0.260* 動機總得分。

2.4 討論

要想增強小學3～5年級學生學習數學的動機，除了要讓學生學會關注數學學習任務，提高自身數學知識和解決數學問題的能力以外，也要激發學生傾向于在數學學習上取得一定的成就，概括為提升數學學習任務的關注度，激發學生內部學習數學的成就動機[6]。

2.5 結論

（1）該問卷的克倫巴赫系數為0.668，可用于施測；KMO 值為0.664，效度尚可。

（2）在F2（掌握—回避定向），以及F6（避免失敗動機）上，男女存在顯著差異，女生比男生更加傾向去避免不能理解或不能掌握的數學學習任務，且女生更加傾向避免失敗。

（3）影響小學3～5年級學生的期中成績最重要的兩個因素是F1（掌握—接近定向）和F5（追求成功動機），F1 除了能直接影響期中成績外，還能通過影響F5 來間接影響期中成績，即追求成功動機的中介效應。

（4）剔除極端值，發現總動機得分的高低也會在一定程度上影響小學生的期中成績。

3 不足與展望

（1）由于取樣只是針對蒲江縣大興九年制義務學校展開調查，在地域上會有一定的限制。

（2）取樣的樣本不夠大，因為經費與時間的限制，該次研究問卷調查只抽取了100 多名學生。

（3）問卷的信效度還有待優化和改進，信效度在0.8 以上是比較良好的狀態。

（4）希望該次研究調查能給后續研究小學生數學學習動機的學者提供一定的參考價值。