二次函數中三角形面積與平行四邊形問題解析

郭建華

二次函數背景下的三角形面積問題及平行四邊形問題是中考的熱點題型，下面舉例進行分析，以幫助同學們總結規律，探尋通法.

原題再現

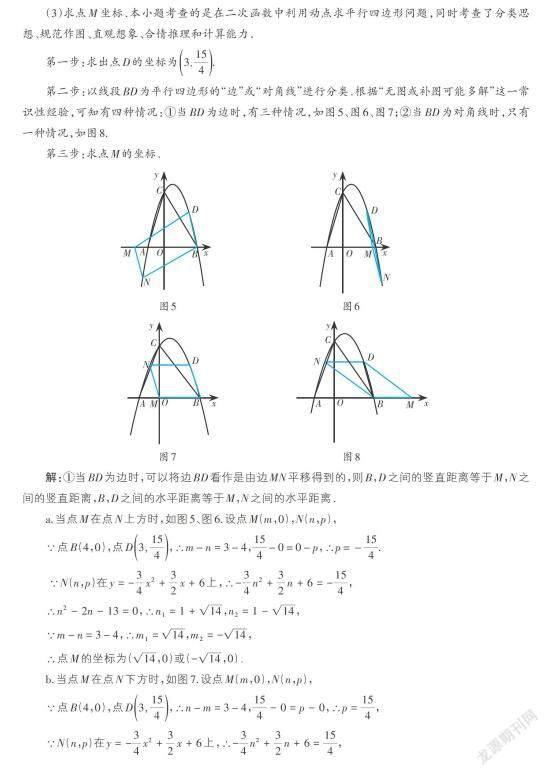
例（2020·甘肅·天水·第26題）如圖1所示，拋物線y=ax2 + bx + c（a ≠ 0）與x 軸交于A，B 兩點，與y軸交于點C，且點A 的坐標為（-2，0），點C 的坐標為（0，6），對稱軸為直線x=1. 點D 是拋物線上一個動點，設點D 的橫坐標為m（1

（1）求拋物線的函數表達式.

（2）當△BCD 的面積等于△AOC 的面積的34時，求m 的值.

（3）在（2）的條件下，若點M 是x 軸上一動點，點N 是拋物線上一動點，試判斷是否存在這樣的點M，使得以點B，D，M，N 為頂點的四邊形是平行四邊形. 若存在，請直接寫出點M 的坐標;若不存在，請說明理由.

分析與拓展

（1）求拋物線的解析式. 本小題考查核心知識點的掌握情況，即待定系數法、解方程組. 求拋物線解析式一般有三種方式可供選擇，即一般式、交點式、頂點式，本題應選用一般式求解. 可得拋物線的函數表達式為y = -34x2 +32x + 6（過程略）.

（2）求m 的值. 本小題考查的是在平面直角坐標系中，給定函數圖形和幾何圖形（三角形），求點的坐標（橫坐標）;同時也考查了推理論證、計算能力和答題過程的嚴謹性.

第一步：根據三個頂點的坐標O（0，0），A（-2，0），C（0，6）直接求出△AOC 的面積.

第二步：求不平行于坐標軸的△BCD（即△BCD 的三邊DB，DC，BC 都不平行于坐標軸，簡稱“斜線三角形”）的面積一般采用割補法;過動點D 作x 軸的垂線，利用割補法將原三角形DBC 分成△DEB 和△DEC，如圖2，使得這兩個三角形可以利用“鉛垂高× 水平寬”求解.

第三步：①求未知直線BC 的函數表達式;②利用垂直于x 軸的直線上任意兩點橫坐標相等，將其縱坐標相減求出鉛垂線段.

第四步：列方程求解.

詳細解答如下：

解：如圖2，過點D 作DE⊥x 軸于F，交BC 于E，過點C 作CH⊥ED，交ED 的延長線于H，

∵點A 的坐標為（-2，0），點C 的坐標為（0，6），

∴OA=2，OC=6，∴S△AOC =12OA ? OC =12× 2 × 6 = 6，

∴S△BCD =34S△AOC =34× 6 =92.

易得點B 的坐標為（4，0），設直線BC 的函數表達式為y=kx + n，

則

ìí?

4k + n = 0，

n = 6，

解得ìí???k = -32，n = 6， ∴直線BC 的函數表達式為y = -32x + 6，

∵點D 的橫坐標為m（1

∴DE = yD - yE = （ ） -34m2 +32m + 6 - （ ） -32m + 6 = -34m2 + 3m，

∵S△BCD = S△CDE + S △BDE，∴S△BCD =12DE ? HC +12DE ? BF =12DE ? OF +12DE ? BF =12DE ? OB，

∴ S△BCD =12（ ） -34m2 + 3m × 4 = -32m2 + 6m，∴-32m2 + 6m =92，

解得：m1=1（不合題意舍去），m2=3. 則當△BCD 的面積等于△AOC 的面積的34時，m 的值為3.

拓展：（1）本題中若將限制條件“1

如：當點D 在點C 左側拋物線上時（如圖3），S△DBC =12DE （ BF - OF ） =12DE ? OB;當點D 在拋物線第四象限部分上時（如圖4），S△DBC =12DE（CH - BF）=12DE·OB.

（3）求點M 坐標.本小題考查的是在二次函數中利用動點求平行四邊形問題，同時考查了分類思想、規范作圖、直觀想象、合情推理和計算能力.

第一步：求出點D的坐標為（3， 15）4 .

第二步：以線段BD 為平行四邊形的“邊”或“對角線”進行分類.根據“無圖或補圖可能多解”這一常識性經驗，可知有四種情況：①當BD 為邊時，有三種情況，如圖5、圖6、圖7;②當BD 為對角線時，只有一種情況，如圖8.

第三步：求點M 的坐標.

解：①當BD 為邊時，可以將邊BD 看作是由邊MN 平移得到的，則B，D 之間的豎直距離等于M，N 之間的豎直距離，B，D 之間的水平距離等于M，N 之間的水平距離.

a.當點M 在點N 上方時，如圖5、圖6.設點M（m，0），N（n，p），

∵點B（4，0），點D（3， 15）4 ，∴m-n = 3-4，154 -0=0-p，∴p=-154 .

∵N（n，p）在y = -34x2 +32x + 6上，∴-34n2 +32n + 6 = -154 ，

∴n2 - 2n - 13 = 0，∴n1 = 1 + 14，n2 = 1 - 14，

∵m-n = 3-4，∴m1 = 14，m2 = - 14，

∴點M 的坐標為（ 14，0）或（- 14，0）.

b.當點M 在點N 下方時，如圖7.設點M（m，0），N（n，p），

∵點B（4，0），點D（3， 15）4 ，∴n-m = 3-4，154 - 0 = p - 0，∴p = 154 ，

∵N（n，p）在y = -34x2 +32x + 6上，∴-34n2 +32n + 6 = 154 ，

∴n2 - 2n - 3 = 0，∴n1 = 3（舍），n2 = -1，

∵n-m = 3-4，∴m = 0，

∴點M 的坐標為（0，0）.

②當BD 為對角線時，如圖8，我們可以發現ND?BM，則點N 的縱坐標等于點D 的縱坐標;再根據平移即可求出點M 坐標.

設點M（m，0），N（n，p），

∵點B（4，0），點D（3， 15）4 ，

∴n-3 = 4-m，154 - 0 = p - 0，∴p = 154 .

∵N（n，p）在y = -34x2 +32x + 6上，

∴-34n2 +32n + 6 = 154 ，

∴n2 - 2n - 3 = 0，∴n1 = 3（舍），n2 = -1，

∵n-3 = 4-m，∴m = 8，∴點M 的坐標為（8，0）.

綜上，點M 的坐標為（ 14，0）或（- 14，0）或（0，0）或（8，0）.

本題小結：在平面直角坐標系中，解決平行四邊形問題，可以利用平行四邊形的性質求解，也可以轉化成平移問題.

跟蹤鞏固

如圖9，直線y = -34x + 3與x 軸交于點C，與y 軸交于點B，拋物線y = ax2 +34x + c 經過B，C 兩點.

（1）求拋物線的解析式;

（2）如圖9，點E 是直線BC 上方拋物線上的一個動點，當△BEC 面積最大時，請求出點E 的坐標和△BEC 面積的最大值.

（3）在（2）的結論下，過點E 作y 軸的平行線交直線BC 于點M，連接AM，點Q 是拋物線對稱軸···上的動點，在拋物線上是否存在點P，使得以P，Q，A，M 為頂點的四邊形是平行四邊形？如果存在，請直接寫出點P 的坐標;如果不存在，請說明理由.

（作者單位：本溪市實驗中學）