促進(jìn)學(xué)生認(rèn)知發(fā)展的教材開發(fā)與重構(gòu)



摘? 要:遵循學(xué)生認(rèn)知規(guī)律,對教材中“基本不等式”的問題情境、典型素材、研究方法等進(jìn)行開發(fā)與重構(gòu),旨在幫助學(xué)生整體理解數(shù)學(xué)知識本質(zhì),促進(jìn)學(xué)生認(rèn)知發(fā)展.
關(guān)鍵詞:基本不等式;認(rèn)知發(fā)展;教材開發(fā);教材重構(gòu)
無論哪個(gè)版本的教材都有其教學(xué)對象的適應(yīng)性,教師在研析《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版)》(以下簡稱《標(biāo)準(zhǔn)》)和教材的同時(shí),應(yīng)深入了解學(xué)生的實(shí)際需要、能力水平和思維習(xí)慣等,創(chuàng)造性使用教材,促進(jìn)學(xué)生全面、主動地建構(gòu)知識體系. 具體而言,教師應(yīng)基于《標(biāo)準(zhǔn)》,充分以學(xué)生的現(xiàn)有水平和實(shí)際需求為出發(fā)點(diǎn),選取適合他們的學(xué)習(xí)材料,對這些材料進(jìn)行加工、處理、整合,使教學(xué)內(nèi)容成為適合學(xué)生學(xué)情的素材. 其目的是將數(shù)學(xué)的學(xué)術(shù)形態(tài)轉(zhuǎn)化為數(shù)學(xué)的學(xué)習(xí)形態(tài),將教材的編寫結(jié)構(gòu)轉(zhuǎn)化為學(xué)習(xí)結(jié)構(gòu),實(shí)現(xiàn)教學(xué)活動的最優(yōu)化.
“基本不等式”是高中數(shù)學(xué)不等式部分的核心內(nèi)容,《標(biāo)準(zhǔn)》將其編于“預(yù)備知識”這一主題中. 本文以此內(nèi)容為研究對象,以蘇教版《普通高中教科書·數(shù)學(xué)》的內(nèi)容為素材,談?wù)劵趯W(xué)生認(rèn)知發(fā)展的學(xué)材重構(gòu)的淺薄思考,敬請指正.
一、情境設(shè)置:應(yīng)基于學(xué)生認(rèn)知起點(diǎn)進(jìn)行考量
《標(biāo)準(zhǔn)》明確指出,要創(chuàng)設(shè)合適的教學(xué)情境,啟發(fā)學(xué)生思考,引導(dǎo)學(xué)生把握數(shù)學(xué)內(nèi)容的本質(zhì). 合理的問題情境使學(xué)生置身于簡潔明了、指向清楚的認(rèn)知任務(wù)中,能有效激發(fā)學(xué)生的求知欲和學(xué)習(xí)心向. 反之,遠(yuǎn)離學(xué)生認(rèn)知起點(diǎn)的問題情境則不能揭示知識本質(zhì),而且會加重學(xué)生的表征負(fù)擔(dān)和認(rèn)知障礙. 例如,用不等臂天平稱物的情境引入幾何平均數(shù)和算術(shù)平均數(shù),旨在從實(shí)際情境中抽象出數(shù)學(xué)對象,有利于培養(yǎng)學(xué)生的數(shù)學(xué)建模能力. 但是在實(shí)際教學(xué)中,部分學(xué)生不能充分調(diào)動已有認(rèn)知進(jìn)行建模活動,也想不到運(yùn)用杠桿原理處理問題,這樣就拉長了數(shù)學(xué)對象出現(xiàn)的時(shí)間,沖淡了情境的教學(xué)功能.
情境的創(chuàng)設(shè)應(yīng)具有能揭示知識本質(zhì)的導(dǎo)向功能,能引發(fā)學(xué)生有效建構(gòu)知識并提供具體而準(zhǔn)確的現(xiàn)實(shí)原型,實(shí)現(xiàn)引領(lǐng)學(xué)生進(jìn)入知識內(nèi)部的邏輯形式和意義領(lǐng)域. 為此,在創(chuàng)新使用教材的理念下,我們可以淡化兩個(gè)平均數(shù)的發(fā)現(xiàn)過程,以公理化的視角從數(shù)學(xué)內(nèi)部引入新知. 從實(shí)數(shù)的非負(fù)性或重要不等式[a2+b2≥2ab]引入基本不等式. 這樣引入的邏輯起點(diǎn)符合學(xué)生的認(rèn)知起點(diǎn),學(xué)習(xí)對象指向精確,減少了因理解情境和表征對象導(dǎo)致的認(rèn)知負(fù)荷,將學(xué)習(xí)的重心落在如何理性認(rèn)識并深度認(rèn)識基本不等式這一核心目標(biāo)上. 因此,可以設(shè)置如下情境.
這樣設(shè)計(jì)的意圖是基于知識之源,突出知識的生長性. 首先,“基本事實(shí)”是基本不等式的根,從學(xué)生已有認(rèn)知結(jié)構(gòu)中的“本源”出發(fā)進(jìn)行上位組織,新知識在“基本事實(shí)”引領(lǐng)下的生成具有生長性,這種生長性體現(xiàn)在還可以將“基本事實(shí)”中的[x]賦成其他對象得到新的恒成立不等式. 其次,對衍生出的恒成立不等式也有多元的操作方式,如還可以用[m=1a,n=][1b]進(jìn)行代換得到[21a+1b≤ab]. 也可以在其兩邊同時(shí)加上一些項(xiàng),如同時(shí)加上[m2+n2],得[2m2+n2≥m+n2].這恰好是最簡單的二維柯西不等式形式. 由此可見,這樣的情境設(shè)置體現(xiàn)了“基本不等式”中“基本”的內(nèi)核所在,即根本的、本源的屬性.
當(dāng)然,情境重構(gòu)的前提應(yīng)是基于學(xué)生的認(rèn)知水平和學(xué)習(xí)需求,并且要以學(xué)生的認(rèn)知發(fā)展為目標(biāo). 脫離學(xué)生認(rèn)知起點(diǎn)和需求的重構(gòu)行為是毫無意義的.
二、幾何解釋:要遵循學(xué)生的認(rèn)知規(guī)律和認(rèn)知方式
教學(xué)中,在提出問題“兩個(gè)正數(shù)[a,b]的算術(shù)平均數(shù)和幾何平均數(shù)之間具有怎樣的大小關(guān)系”后,直接引導(dǎo)學(xué)生以幾何的視角對其進(jìn)行驗(yàn)證猜想,并嘗試作出長度為[ab]和[a+b2]的兩條線段. 實(shí)際上,如果沒有教師的引導(dǎo),學(xué)生在同一個(gè)圖形(如圖1,其中AC = a,BC = b)中作出這樣的幾何對象是非常困難的.
從整個(gè)認(rèn)知的路線看,這里也略顯突兀:從情境中抽象出對象[ab]和[a+b2],再通過數(shù)值驗(yàn)證兩者的大小關(guān)系,至此的認(rèn)知活動以“推理—演算”為主要方式,正當(dāng)學(xué)生初步形成建立兩者關(guān)系的“感覺”時(shí)讓學(xué)生切換認(rèn)知方式,從另一個(gè)認(rèn)知視角(即幾何)來驗(yàn)證正處于“模糊”狀態(tài)下的認(rèn)知對象. 一方面,會導(dǎo)致學(xué)生在認(rèn)知方式的轉(zhuǎn)頻上產(chǎn)生間歇性困難,學(xué)生可能會出現(xiàn)思維上的斷層;另一方面,根據(jù)概念二重性理論,一個(gè)概念的形成要從過程開始,然后轉(zhuǎn)變?yōu)閷ο蟮恼J(rèn)知過程. 顯然,之前的代數(shù)值驗(yàn)證活動是概念認(rèn)知的過程階段,此時(shí)的認(rèn)知更多是感性的,而之后的“作圖驗(yàn)證”屬于幾何表征,是在獲得結(jié)論(即[a+b2≥ab])的基礎(chǔ)之上進(jìn)行的概念認(rèn)知的對象階段,很明顯這個(gè)過程中出現(xiàn)了認(rèn)知方式上的混亂,不利于概念的理性建構(gòu).
筆者認(rèn)為,本節(jié)課的認(rèn)知路線應(yīng)該是“不等式的發(fā)現(xiàn)—不等式的證明—不等式的欣賞”,遵循從感性認(rèn)識到理性認(rèn)識再到深度認(rèn)識的逐步認(rèn)知數(shù)學(xué)對象的原則. 基于此,建議將素材的順序調(diào)整為:發(fā)現(xiàn)[a+b2≥][ab]—代入數(shù)值進(jìn)一步驗(yàn)證—運(yùn)用不同的方法進(jìn)行證明—從其他角度(幾何、函數(shù)等)進(jìn)行欣賞,促使學(xué)生形成深度理解.
這樣的調(diào)整是將幾何表征作為概念建構(gòu)后進(jìn)行數(shù)學(xué)欣賞的一個(gè)視角,具有可操作性,并且這樣的設(shè)計(jì)也有可生長性. 例如,在后面學(xué)習(xí)了初等函數(shù)后,可借助初等函數(shù)的性質(zhì)來幫助學(xué)生進(jìn)一步理解基本不等式的本質(zhì)屬性. 實(shí)際上,在學(xué)習(xí)了冪函數(shù)、指數(shù)函數(shù)、對數(shù)函數(shù)后,教材中都設(shè)置了“比較[fx1+fx22]與[fx1+x22]的大小關(guān)系”的題目. 這樣的設(shè)計(jì)既是基于對知識整體認(rèn)知的考慮,也為再度理解基本不等式的本質(zhì)提供了新視角.
三、證法選擇:從單元學(xué)習(xí)的視角進(jìn)行整體認(rèn)知
布魯納說過,無論我們選教什么學(xué)科,都務(wù)必使學(xué)生理解學(xué)科的基本結(jié)構(gòu). 從整個(gè)學(xué)習(xí)單元來看,實(shí)數(shù)大小關(guān)系的基本事實(shí)是解決等式、不等式問題的邏輯基礎(chǔ). 通過類比等式的性質(zhì)獲得不等式的性質(zhì),并以此進(jìn)一步研究基本不等式等是本章的學(xué)習(xí)主線. 因此,研究基本不等式的認(rèn)知起點(diǎn)應(yīng)是實(shí)數(shù)的大小關(guān)系. 筆者認(rèn)為,作差法應(yīng)該是證明基本不等式的首選方法,這樣的選擇體現(xiàn)了單元教學(xué)的邏輯性,突出了知識的生成是之前認(rèn)知的延續(xù)與生長.
分析法的核心是從證明的結(jié)論出發(fā),逐步尋求使其成立的充分條件. 在前一章中學(xué)生已經(jīng)學(xué)習(xí)了命題和充要條件,能夠認(rèn)識到進(jìn)行證明的邏輯依賴于命題的充要性,而實(shí)施分析法的充要性就是以本章上一節(jié)中的不等式的性質(zhì)為邏輯依據(jù),分析法實(shí)際上是在不等式性質(zhì)的基礎(chǔ)上進(jìn)行的推理展示. 盡管這樣的逆向思維是學(xué)生之前認(rèn)知結(jié)構(gòu)中所沒有的,但是它是基于已有認(rèn)知的邏輯存在. 因此,分析法是符合學(xué)生認(rèn)知整體性和邏輯性的.
綜合法的證明過程實(shí)際上是前文所述的基于基本事實(shí)的演繹過程,即從[?x∈R],[x2≥0]出發(fā),取[x=][a-b]進(jìn)行的變形,通過分析,認(rèn)為將其視為發(fā)現(xiàn)對象的途徑比其作為證明方法的教學(xué)功能更豐富.
通過以上分析可知,方法的選擇要充分考慮方法在學(xué)生認(rèn)知系統(tǒng)中的整體性,并且還要考慮選擇的方法對學(xué)生解決相關(guān)問題的思維方式形成方面的影響. 因此,三種方法的使用可以調(diào)整成如下的組織結(jié)構(gòu):綜合法作為不等式發(fā)現(xiàn)的方法—從比較大小的角度選擇作差法證明—從運(yùn)用不等式性質(zhì)及邏輯的角度選擇分析法證明.
值得說明的是,這三種方法是不是都要講?是不是一定要照此來講?教無定法,貴在得法. 筆者認(rèn)為,應(yīng)該以單元學(xué)習(xí)的整體視角來審視證明方法的選擇,有什么樣的目標(biāo)定位就選擇什么樣的證明方法(或方法的組合),靈活整合這些方法進(jìn)行講評,不能孤立地將其作為證明的某一種方法進(jìn)行傳授,而應(yīng)作為整體認(rèn)知中某一個(gè)邏輯點(diǎn)來考量.
四、弦圖處理:在已有活動經(jīng)驗(yàn)中進(jìn)行深度認(rèn)知
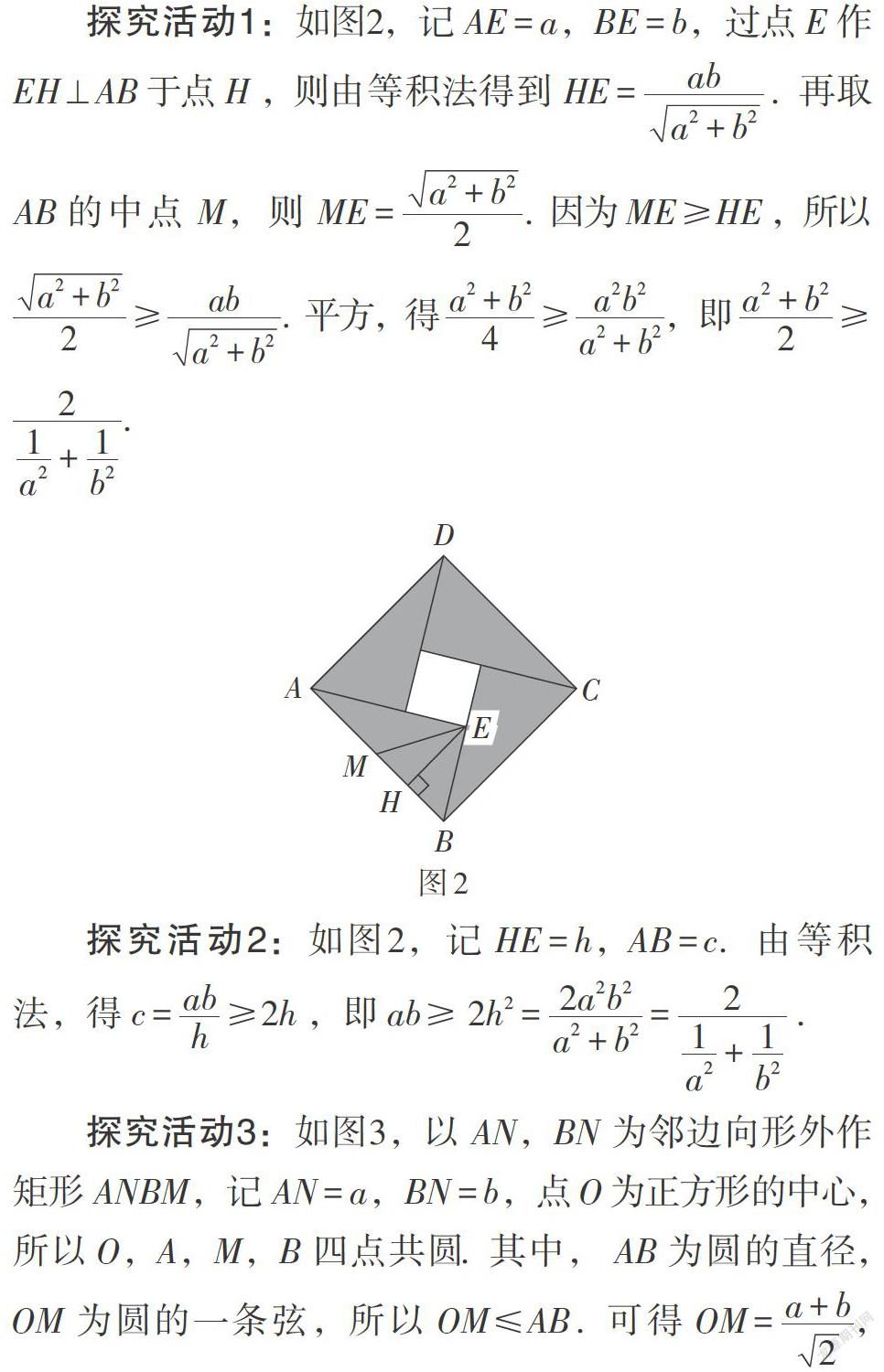
趙爽弦圖是經(jīng)典的教學(xué)素材,其結(jié)構(gòu)精妙、內(nèi)涵豐富,是數(shù)與形完美統(tǒng)一的典范. 各版新教材很重視對該素材的使用及教學(xué)功能的開發(fā):人教A版在正文中以“探究”的方式認(rèn)知趙爽弦圖中蘊(yùn)含的相等關(guān)系和不等關(guān)系;北師大版在閱讀材料介紹趙爽弦圖并揭示其中蘊(yùn)含的不等關(guān)系;蘇教版以“練習(xí)題”的方式要求學(xué)生指出趙爽弦圖的構(gòu)成,并直接說明其中存在著的不等關(guān)系;湘教版在正文中以問題的形式構(gòu)建出[a2+b2>][2ab]. 除此之外,我們還可以充分挖掘趙爽弦圖的教學(xué)功能,引導(dǎo)學(xué)生在已有活動經(jīng)驗(yàn)的基礎(chǔ)上進(jìn)行深度的認(rèn)知活動.
學(xué)生在初中階段已經(jīng)借助趙爽弦圖研究了勾股定理,學(xué)習(xí)基本不等式時(shí)再次運(yùn)用趙爽弦圖進(jìn)行研究,學(xué)生已經(jīng)具備一定的認(rèn)知經(jīng)驗(yàn)——同樣的圖象背景和認(rèn)知方式(均是從幾何圖形中構(gòu)建代數(shù)關(guān)系),不同的問題指向(從等量關(guān)系到不等關(guān)系),這些都是認(rèn)知經(jīng)驗(yàn)的延續(xù)與拓展. 實(shí)際上,在教學(xué)中可以引導(dǎo)學(xué)生利用該學(xué)材進(jìn)行以下探究性活動.
顯而易見,上述探究活動和之前通過弦圖發(fā)現(xiàn)(或幾何解釋)基本不等式的認(rèn)知方式保持一致,是在已有活動經(jīng)驗(yàn)下進(jìn)行的探究,而且獲得的結(jié)論是經(jīng)典的不等式鏈,學(xué)生能夠再次感受到幾何圖形中蘊(yùn)含著的代數(shù)關(guān)系的統(tǒng)一美與和諧美,進(jìn)而帶著這樣的認(rèn)知經(jīng)驗(yàn)和鑒賞體驗(yàn)去探求更豐富的數(shù)學(xué)結(jié)論,這無疑對學(xué)生進(jìn)行深度認(rèn)知是有促進(jìn)意義的.
總之,教材是教學(xué)活動開展的行動指南. 在使用教材的過程中,不僅要充分尊重教材,理解教材編寫思路和編者意圖,充分認(rèn)識教材所承載的學(xué)科功能與教育價(jià)值,還要理性考量教材中的素材,創(chuàng)造性地使用教材,以學(xué)生的認(rèn)知和數(shù)學(xué)的邏輯來審視教學(xué)素材,結(jié)合教學(xué)的實(shí)際情況進(jìn)行重構(gòu),真正發(fā)揮教材的教育教學(xué)價(jià)值,促進(jìn)學(xué)生對知識本質(zhì)的理解.
參考文獻(xiàn):
[1]張奠宙. 用不等臂天平稱物導(dǎo)出基本不等式的得與失[J]. 數(shù)學(xué)教學(xué),2016(6):封底.
[2]丁益民.“基本不等式”教學(xué)中幾個(gè)環(huán)節(jié)的思考[J]. 數(shù)學(xué)通訊,2011(12):18-20.
[3]張宗余,張穎. 充實(shí)、剪裁、編排、活化:整合不同版本教材優(yōu)化教學(xué)設(shè)計(jì)的四個(gè)維度[J]. 中學(xué)數(shù)學(xué)教學(xué)參考(上旬),2018(3):6-10.
[4]鐘志華,李渺. 基于變式教學(xué)的數(shù)學(xué)教學(xué)設(shè)計(jì):以“基本不等式”為例[J]. 數(shù)學(xué)通報(bào),2019,58(5):23-27.

