高中數(shù)學解題錯因分析及對策

阮蓮花

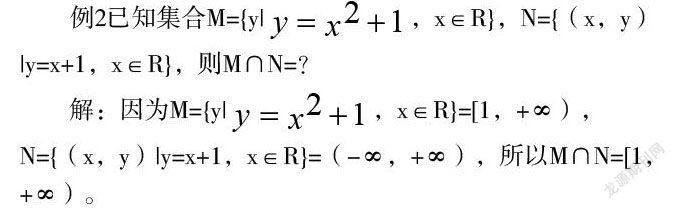
摘要：學生做題時產(chǎn)生錯誤的原因可能有多種。主要分為智力因素和非智力因素兩大類。如對一些概念性質(zhì)模糊，忽視了一些公式定理成立的條件，違反了證明規(guī)則。不能正確的運用數(shù)學思想方法如分類討論考慮不全面;審題不清，由于慣性思維對題目主觀臆斷[1];對公式機械記憶導致混淆錯誤運用;由于粗心大意導致的錯誤。本文通過一些典型的例題對應分析學生做題產(chǎn)生的錯誤原因并提出糾錯策略，以幫助學生找到薄弱點提高數(shù)學成績和為教師教學提供一點啟示。

關鍵詞：數(shù)學解題;錯因分析;糾錯策略

引言

數(shù)學以其特有的思維性，令許多學生望而生畏，尤其是高中數(shù)學。但是其實不管什么學科，都有一定的方法蘊含其中，只要理解掌握了，數(shù)學可以成為你的優(yōu)勢學科，數(shù)學能通過人的邏輯推理和分析思維能力，學好數(shù)學也有助于學好物理和化學。在解題中，一道題中可能涉及了一些數(shù)學思想方法及一系列的定理公式和概念性質(zhì)的應用。很多人不停地刷題鍛煉自己的能力，事實上大部人做完成堆的題效果并不明顯，是因為他們抓不住重難點，沒有真正理解和掌握總結(jié)，刷再多題也是無用功，題不在于多而在于精。學好數(shù)學重要是方法和知識體系的前后聯(lián)系，學會總結(jié)反思，把一些題和方法歸類，深入理解和鞏固。在學習和做題中反思分析錯題錯因是很有必要的，對于學生而言可以找到自己的薄弱點，對癥下藥;對于教師可以發(fā)現(xiàn)學生的錯誤反思和改進教學，充分備課。下面結(jié)合自己的實踐體驗分析一些易錯題的錯因及相應的教學改進策略。

一、對一些概念性質(zhì)模糊導致的錯誤

這是學生學習過程中出錯的一個重要原因，學習概念時沒有理解概念的內(nèi)涵和外延，不能把握準概念。一些看似簡單的題目，稍微變式一下，做題就感到模棱兩可，所以一定要深入理解概念。

例1設M={1、2、3}，N={e、g、h}，從M至N的四種對應方式，其中是從M到N的映射是（B）

錯因分析：本題考查映射的概念和特點，學生出現(xiàn)錯誤的原因是對映射的概念和特點不清楚，以及與函數(shù)概念的聯(lián)系和區(qū)別模糊。對映射是否能一對多還是多對一混淆。根據(jù)映射的特點不能“一對多”：A中不能有剩余元素，B中可以有剩余元素。所以A、B、D都錯誤;只有C完全滿足映射與函數(shù)〈特殊對應）的全部5個特點。

教師在講解概念和這類題目時應舉一些例子，使學生在完全掌握概念的基礎上，靈活掌握變型題。并且講清楚映射和函數(shù)的聯(lián)系和區(qū)別以及各自的特點，引導學生觀察對比區(qū)別他們的不同之處，深入理解記憶。函數(shù)是特殊的映射，是數(shù)集到數(shù)集的映射，映射是函數(shù)概念的擴展，映射不一定是函數(shù)。映射與函數(shù)（特殊對應）的共同特點：可以是“一對一”;可以是“多對一”;不能“一對多”。

錯因分析：出現(xiàn)錯誤的原因是沒有注意到構(gòu)成兩個集合的元素是不同的，即集合M是數(shù)集，而集合N是點集，兩個集合是性質(zhì)完全不同的集合，不能做運算。

因為集合N是一個點集，不是數(shù)集，即集合N表示直線y=x+1上所有的點，而不是（一∞，+∞）。所以集合M∩N=0。

集合的概念是高中數(shù)學最基礎的概念，集合知識是為后續(xù)學習做準備的基礎知識。教師在講解集合知識的時候，應著重講解集合的性質(zhì)，特別需要教師強調(diào)的是構(gòu)成集合元素的特征。

二、對于一些公式定理理解不清或混淆而導致的錯誤

沒有注意公式定理的前提條件，從而擴大其使用范圍等，都可能導致解題出錯。如利用均值不等式求最值時，對一正二定三相等的條件理解不透徹，忽略了求最值的法則及不等式成立的條件而導致錯誤結(jié)果[2]。學生往往會因為忽視這三個條件中的某個而出錯。

學生1：因為|a-b|=|b|，所以a-b=b或a-b=-b，故a=2b或a=0（舍去），所以|a-2b|=0，由于b是非零向量，所以|2b|>0，故|2b|>|a-2b|，選A。

學生2：因為|a-b|=|b|，所以（a-b）（a-b）=b·b，a·a-2a·b+b·b=b·b，

所以a·a=2a·b，所以a=2b，故|a-2b|=0。由于b是非零向量，所以|2b|>0，故|2b|>|a-2b|.選A。

教師在講解該內(nèi)容時可以引導學生畫圖，數(shù)形結(jié)合可以使學生更直觀的理解和比較大小關系。說明向量運算與實數(shù)運算的本質(zhì)區(qū)別，向量運算不僅涉及向量的長度，還涉及向量的方向。在實數(shù)運算中，若a≠0且ab=0則b=0。但在向量運算中若a≠0且ab=0則有兩種情況b=0或a⊥b[3]。

三、運用數(shù)學思想方法如分類討論考慮不全面

分類討論是解決問題的一種邏輯方法，也是一種數(shù)學思想，這種思想對于簡化研究對象，發(fā)展人的思維有著重要幫助。分類討論是具有較高的邏輯性及很強的綜合性，培養(yǎng)學生思維的條理性，縝密性，科學性，所以在數(shù)學解題中占有重要的位置。分類原則：分類對象確定，標準統(tǒng)一，不重復，不遺漏，分層次，不越級討論[4]。但是在解題中學生容易因為分類標準和層次不清楚而導致一些錯誤。

錯因分析：該學生沒有考慮直線L的斜率不存在的情況。可能出現(xiàn)的原因有以下幾點：①該學生忽略了直線點斜式方程的局限性（點斜式方程不能表示斜率不存在的直線）;②該學生對分類討論思想的運用不熟練：③該學生對圓與直線的位置關系考慮得不全面。

正確解法：①當直線L的斜率不存在時，根據(jù)題意所求直線l的方程為x=2;②當直線L的斜率存在且設為k時，方法如上。綜上，所求直線L的方程為x=2或4x-3y+1=0

教師應該根據(jù)該題的教學步驟，在教學過程中，采取相應策略設置問題。

教師提出問題，“過圓外一點能作幾條圓的切線”，讓學生畫出該題相關的圖像，“直線L與圓相切有幾種情況？”引導學生根據(jù)直線斜率的存在情況運用分類討論思想解題，可設置問題如“當斜率存在時，直線L的方程如何求得？”當斜率不存在時，直線L的方程是什么？

四、審題不清，由于慣性思維對題目主觀臆斷;對公式機械記憶導致混淆錯誤運用;由于粗心大意導致的錯誤

例7已知雙曲線的右準線為x=4，右焦點F（10，0），離心率e=2，求雙曲線的方程。

五、總結(jié)

總的來說，我認為教師可以從以下幾點著手①在新知識的教學時注重突出基礎知識、基本概念，在學生知識和思維的薄弱點設置教學環(huán)節(jié)，說明相關概念之間的聯(lián)系和區(qū)別，加入適當?shù)淖兪骄毩暎瑤椭鷮W生真正掌握知識點。深入理解公式定理的成立條件和證明過程，不能停留在機械表面的記憶層面。②在日常學習、練習中養(yǎng)成正確的學習習慣和思維習慣。比如，整潔的草稿紙是理性思維的外在表象。做題時不是一味求快，要認真仔細，適當?shù)臅r候“瞻前顧后”，把握整體，對已知條件、已得結(jié)論、所求結(jié)果等統(tǒng)籌把握，而不是想到什么寫什么。在易錯點、特殊點處能重點對待，引導學生總結(jié)反思，及時糾正錯誤。③養(yǎng)成良好的心態(tài)。考試中由于緊張的氣氛和時間的限制會出現(xiàn)-些“粗心”，會把“+”誤寫成“一”，“<”誤寫成“>”等。因此，在日常學習中養(yǎng)成良好的心態(tài)也是減少做題出錯的關鍵。

參考文獻：

[1]劉發(fā).初中數(shù)學易錯題錯因分析及糾錯策略[J].數(shù)學教學通訊，2015（000）004.

[2]何彩云.用基本不等式求最值的常見錯誤例析[J].教育科學，2014（01）

[3]徐靜.高中數(shù)學解題錯誤的原因分析及對策[J].數(shù)理化學習，2018（11）

[4]趙新五.淺談高中數(shù)學分類討論中的易錯點[J].試題與研究，2011（10）