“數(shù)學(xué)建模活動——茶水最佳飲用時間”教學(xué)設(shè)計(jì)

韓慧

摘? 要：本節(jié)課在“互聯(lián)網(wǎng) +”教學(xué)條件下，通過“茶水最佳飲用時間”的問題背景，呈現(xiàn)了師生共同完成數(shù)學(xué)建模活動選題、開題、做題、結(jié)題的全過程. 在信息技術(shù)支持下，學(xué)生通過實(shí)踐操作、任務(wù)探究建立函數(shù)模型解決實(shí)際問題，感知數(shù)學(xué)建模的一般方法和數(shù)學(xué)思想，提升了應(yīng)用意識和創(chuàng)新能力，促進(jìn)了數(shù)學(xué)學(xué)科核心素養(yǎng)的形成和發(fā)展.

關(guān)鍵詞：數(shù)學(xué)建模;信息技術(shù);教學(xué)實(shí)踐

一、教學(xué)內(nèi)容解析

“數(shù)學(xué)建模活動——茶水最佳飲用時間”是人教A版《普通高中教科書·數(shù)學(xué)（必修）》第一冊“建立函數(shù)模型解決實(shí)際問題”的內(nèi)容. 在高中階段，學(xué)生將經(jīng)歷從數(shù)學(xué)知識的直接應(yīng)用與滲透到自主完成數(shù)學(xué)建模活動的過程. 本節(jié)課是在學(xué)生學(xué)習(xí)了指數(shù)函數(shù)、對數(shù)函數(shù)和冪函數(shù)的基礎(chǔ)上，通過建立函數(shù)模型解決實(shí)際問題，師生共同完成選題、開題、做題、結(jié)題全過程. 通過本節(jié)課的學(xué)習(xí)，使學(xué)生進(jìn)一步加深對函數(shù)模型的理解和認(rèn)識，熟悉數(shù)學(xué)建模活動的一般流程，為后續(xù)研究其他函數(shù)模型的應(yīng)用及自主完成數(shù)學(xué)建模活動全過程提供數(shù)學(xué)思想和方法指導(dǎo).

通過數(shù)學(xué)建模活動的開展，學(xué)生能有意識地用數(shù)學(xué)語言表達(dá)世界，發(fā)現(xiàn)問題和提出問題，感悟數(shù)學(xué)與現(xiàn)實(shí)之間的關(guān)聯(lián);學(xué)會用數(shù)學(xué)模型解決實(shí)際問題，積累數(shù)學(xué)實(shí)踐經(jīng)驗(yàn)，認(rèn)識數(shù)學(xué)模型在現(xiàn)實(shí)生活中的作用，提升實(shí)踐能力、增強(qiáng)創(chuàng)新意識.

二、教學(xué)目標(biāo)設(shè)置

本節(jié)課教學(xué)目標(biāo)設(shè)置如下.

（1）能對現(xiàn)實(shí)問題進(jìn)行數(shù)學(xué)抽象，準(zhǔn)確收集數(shù)據(jù)，正確分析數(shù)據(jù)，建立適當(dāng)?shù)暮瘮?shù)模型，利用信息技術(shù)工具求解模型、檢驗(yàn)?zāi)Ｐ汀?yōu)化模型，最終達(dá)到解決實(shí)際問題的目的.

（2）經(jīng)歷數(shù)學(xué)建模活動的全過程，感知建立函數(shù)模型解決實(shí)際問題的一般方法，體會現(xiàn)實(shí)世界與數(shù)學(xué)知識之間的緊密聯(lián)系，在探究的過程中提升應(yīng)用意識和創(chuàng)新能力.

本節(jié)課教學(xué)重點(diǎn)：函數(shù)模型的建立、檢驗(yàn)與優(yōu)化.

三、學(xué)生學(xué)情分析

本節(jié)課的授課對象為山東省青島第二中學(xué)分校創(chuàng)新學(xué)院的學(xué)生，他們思維活躍，能熟練運(yùn)用信息技術(shù)工具輔助學(xué)習(xí)，并且有豐富的探究活動經(jīng)驗(yàn).

1. 學(xué)生已有的認(rèn)知基礎(chǔ)

“數(shù)學(xué)建模活動——茶水最佳飲用時間”課與學(xué)生的生活密切相關(guān)，便于學(xué)生獲取和了解相關(guān)的背景知識. 學(xué)生已經(jīng)學(xué)習(xí)了指數(shù)函數(shù)、對數(shù)函數(shù)和冪函數(shù)的相關(guān)知識，掌握了函數(shù)模型應(yīng)用的基本方法與步驟，具備了從圖象直觀上獲得結(jié)論和根據(jù)數(shù)量關(guān)系進(jìn)行邏輯推理的能力，這些為本節(jié)課建立函數(shù)模型解決實(shí)際問題做了鋪墊.

2. 達(dá)成教學(xué)目標(biāo)所需具備的認(rèn)知基礎(chǔ)

數(shù)學(xué)建模活動對學(xué)生綜合能力要求較高，包括將實(shí)際問題轉(zhuǎn)化為數(shù)學(xué)問題的能力，挖掘信息、收集數(shù)據(jù)、分析數(shù)據(jù)，建立、求解、檢驗(yàn)、優(yōu)化、應(yīng)用模型等能力.

3.“已有的基礎(chǔ)”與“需要的基礎(chǔ)”之間的差異

如何檢驗(yàn)和優(yōu)化數(shù)學(xué)模型，對學(xué)生來說比較困難.

4. 教學(xué)難點(diǎn)及其突破策略

教學(xué)難點(diǎn)：函數(shù)模型的檢驗(yàn)和優(yōu)化.

突破策略：通過教師的啟發(fā)引導(dǎo)、學(xué)生小組的團(tuán)隊(duì)合作完成核心任務(wù)探究. 同時，發(fā)揮信息技術(shù)的輔助功能.

四、教學(xué)策略分析

1. 教學(xué)策略

（1）依據(jù)數(shù)學(xué)建模活動的內(nèi)容和要求組織教學(xué)材料. 通過精心設(shè)計(jì)的問題，引導(dǎo)學(xué)生利用已有函數(shù)知識在實(shí)際問題中構(gòu)建具體的函數(shù)模型開展建模活動，歸納出數(shù)學(xué)建模活動的一般方法，幫助學(xué)生形成完整的認(rèn)知結(jié)構(gòu).

（2）依據(jù)學(xué)情組織教學(xué)活動. 根據(jù)學(xué)生的思維特點(diǎn)和認(rèn)知基礎(chǔ)，對重、難點(diǎn)內(nèi)容——函數(shù)模型的建立、檢驗(yàn)與優(yōu)化采用核心任務(wù)探究的教學(xué)方式，在每個核心任務(wù)下設(shè)置子任務(wù)，通過獨(dú)立思考、小組合作、展示交流、質(zhì)疑追問、互評反思等師生活動來強(qiáng)化重點(diǎn)、突破難點(diǎn). 學(xué)生在嘗試和探索中掌握數(shù)學(xué)建模活動的數(shù)學(xué)思想和一般方法.

（3）突出數(shù)學(xué)思想方法的提煉和滲透. 通過將抽象的知識具體化、有序化、開放化，在引導(dǎo)學(xué)生主動建構(gòu)數(shù)學(xué)知識的同時，保持積極有效的思維活動，培養(yǎng)學(xué)生的批判性思維、開放性視野，提升學(xué)生分析問題和解決問題的能力、交流合作能力、數(shù)學(xué)語言表達(dá)能力，發(fā)展學(xué)生的數(shù)學(xué)建模、數(shù)學(xué)抽象、數(shù)據(jù)分析、數(shù)學(xué)運(yùn)算、邏輯推理和直觀想象素養(yǎng).

（4）運(yùn)用“互聯(lián)網(wǎng) + ”教學(xué)提高效率. 學(xué)生借助數(shù)學(xué)軟件建模，體會利用信息技術(shù)解決程序化問題的優(yōu)越性，在嘗試和探索中掌握方法、體會思想、形成技能;教師借助信息技術(shù)工具的統(tǒng)計(jì)功能實(shí)時掌握學(xué)情，為不同基礎(chǔ)的學(xué)生提供適當(dāng)?shù)膸椭皶r反饋學(xué)生在學(xué)習(xí)過程中出現(xiàn)的問題，提高教學(xué)效率.

2. 教學(xué)資源

平板電腦、GeoGebra軟件、MATLAB軟件、投影儀、計(jì)算機(jī)、數(shù)據(jù)采集器、溫度傳感器、多媒體課件.

五、教學(xué)過程設(shè)計(jì)

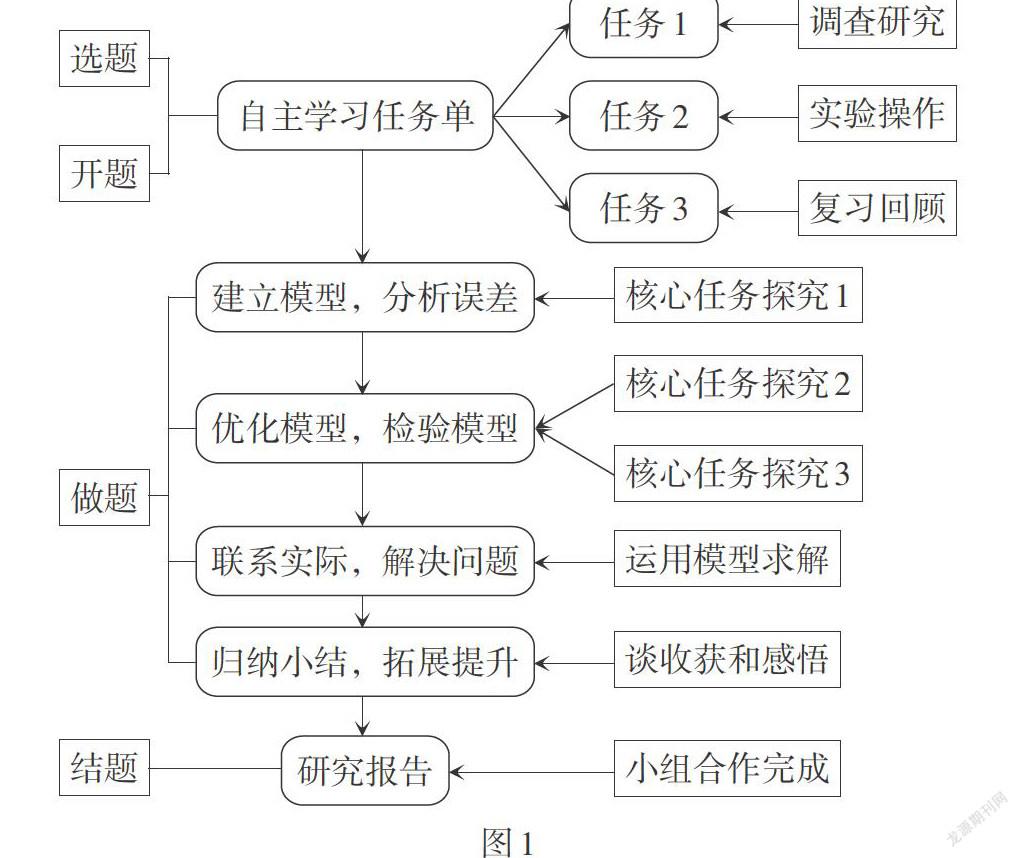
本次數(shù)學(xué)建模活動分為選題、開題、做題、結(jié)題四個部分，如圖1所示. 此活動并非一個課時能夠完成，因此課前留給學(xué)生3天時間完成了選題、開題工作，課上以做題為主，即完成數(shù)學(xué)建模活動的主要過程，課后學(xué)生自主完成結(jié)題工作.

1. 選題、開題

課前設(shè)置自主學(xué)習(xí)任務(wù)單幫助學(xué)生選題、開題，讓學(xué)生通過調(diào)查研究、實(shí)驗(yàn)操作、復(fù)習(xí)回顧，為課堂上的做題做好準(zhǔn)備. 自主學(xué)習(xí)任務(wù)單包含以下三項(xiàng)任務(wù).

任務(wù)1：調(diào)查研究影響茶水口感的因素有哪些，主要因素是什么.

學(xué)生活動：分小組查閱資料、現(xiàn)場咨詢，由班長匯總、整理，在課上展示.

【設(shè)計(jì)意圖】培養(yǎng)學(xué)生通過查閱資料、現(xiàn)場咨詢等渠道獲取信息的能力.

任務(wù)2：以小組為單位，收集茶水溫度隨時間變化的數(shù)據(jù).

要求：測量時間間隔為1分鐘.

提供工具：計(jì)算機(jī)、數(shù)據(jù)采集器、溫度傳感器、室溫計(jì)、綠茶、陶瓷茶具、山泉水、電熱水壺.

學(xué)生活動：各小組分別完成實(shí)驗(yàn)，收集數(shù)據(jù)，由數(shù)據(jù)處理員匯總.

【設(shè)計(jì)意圖】讓每位學(xué)生親身經(jīng)歷通過實(shí)驗(yàn)收集數(shù)據(jù)的過程.

任務(wù)3：回顧已學(xué)函數(shù)的定義、圖象和性質(zhì)，形成思維導(dǎo)圖.

【設(shè)計(jì)意圖】學(xué)生自主梳理函數(shù)知識結(jié)構(gòu)，為后續(xù)建立函數(shù)模型解決實(shí)際問題做準(zhǔn)備.

2. 做題

（1）選題、開題，展示匯報(bào).

師生活動：中國茶文化源遠(yuǎn)流長，并且與學(xué)生實(shí)際生活密切相關(guān). 課上先由“中國·茶”視頻引入學(xué)生所選課題，然后由班長匯報(bào)相關(guān)背景知識的調(diào)研成果，得出影響茶水口感的最主要因素是茶葉類型和水的溫度. 隨之引出問題：青島盛產(chǎn)綠茶，以此作為研究對象，調(diào)查表明，用85 ℃的水泡制茶葉，再等到茶水溫度降至60 ℃時飲用，口感最佳. 剛泡好的茶水大約需要放置多長時間才能達(dá)到最佳飲用口感呢？學(xué)生從這樣一個實(shí)際問題中抽象出數(shù)學(xué)問題——建立茶水溫度隨時間變化的函數(shù)模型，進(jìn)而自主設(shè)計(jì)出合理可行的研究方案.

【設(shè)計(jì)意圖】滲透中國茶文化，讓學(xué)生感受數(shù)學(xué)來源于生活，又服務(wù)于生活，激發(fā)學(xué)生的學(xué)習(xí)興趣. 活動幫助學(xué)生從實(shí)際問題中抽象出數(shù)學(xué)本質(zhì)，明確研究的內(nèi)容，培養(yǎng)學(xué)生用數(shù)學(xué)眼光觀察世界的能力和數(shù)學(xué)抽象能力.

學(xué)生活動：按照研究方案，課前學(xué)生根據(jù)模型假設(shè)在25 ℃的室溫下用85 ℃的水泡制綠茶，利用計(jì)算機(jī)、數(shù)據(jù)采集器、溫度傳感器等設(shè)備，每隔1分鐘測量一次茶水溫度，得到茶水溫度隨時間變化的數(shù)據(jù)，課堂上由數(shù)據(jù)處理員展示匯報(bào).

【設(shè)計(jì)意圖】收集數(shù)據(jù)是數(shù)學(xué)建模的必備能力，學(xué)生通過實(shí)驗(yàn)獲得數(shù)據(jù)，這一過程對于提升學(xué)生的數(shù)據(jù)分析能力有很大幫助.

有了課前的充分準(zhǔn)備，下面學(xué)生正式開始做題.

（2）建立模型，分析誤差（重點(diǎn)）.

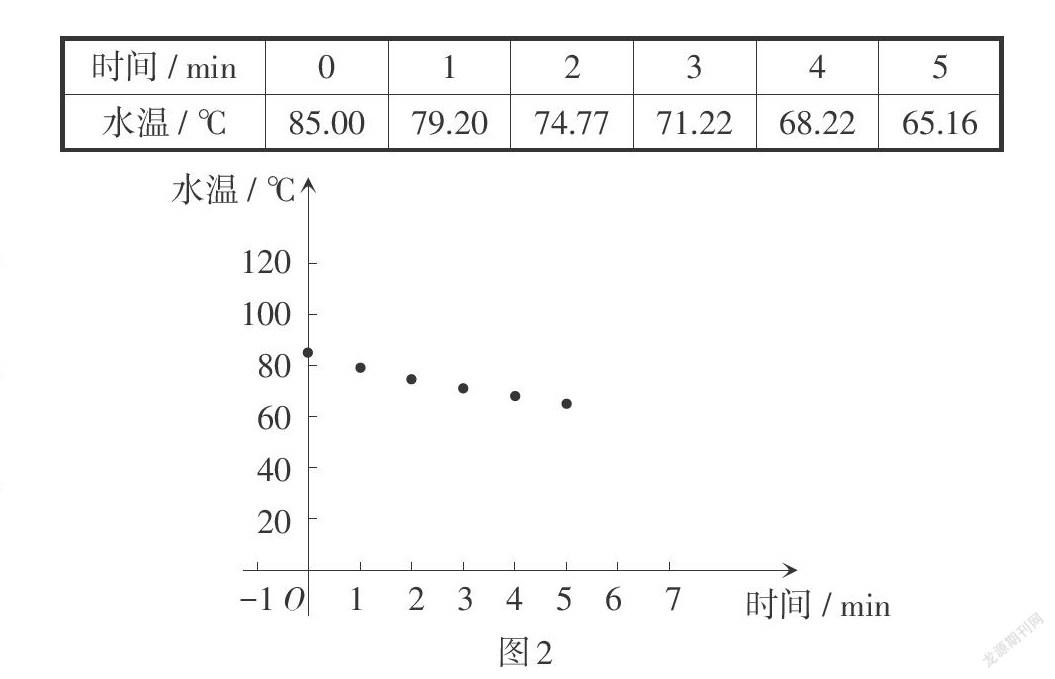
師生活動：從大量的實(shí)驗(yàn)數(shù)據(jù)中隨機(jī)選取一組（如下表）作為研究對象. 以時間為橫軸、水溫為縱軸，利用GeoGebra軟件作出散點(diǎn)圖（如圖2）進(jìn)行直觀描述，進(jìn)而引導(dǎo)學(xué)生用更加準(zhǔn)確的數(shù)學(xué)語言，即函數(shù)解析式進(jìn)行刻畫.

【設(shè)計(jì)意圖】數(shù)據(jù)表格—幾何直觀—代數(shù)表示，這一由具體到抽象的過程幫助學(xué)生提升了直觀想象能力和數(shù)據(jù)分析能力.

核心任務(wù)探究1：小組合作，每組選擇一種函數(shù)，要求如下. ① 利用GeoGebra軟件作出散點(diǎn)圖，選擇函數(shù)模型，顯示擬合曲線及解析式;② 進(jìn)行誤差分析;③ 預(yù)測30分鐘之后的水溫;④ 對該模型進(jìn)行評價.

完成后拍照提交，每個小組提交一份，隨后由小組代表展示講解.

師生活動：各小組選擇并建立了四種函數(shù)模型：一次函數(shù)、二次函數(shù)、冪型函數(shù)、指數(shù)型函數(shù). 小組代表分別進(jìn)行展示匯報(bào)，小組之間展開互動交流.

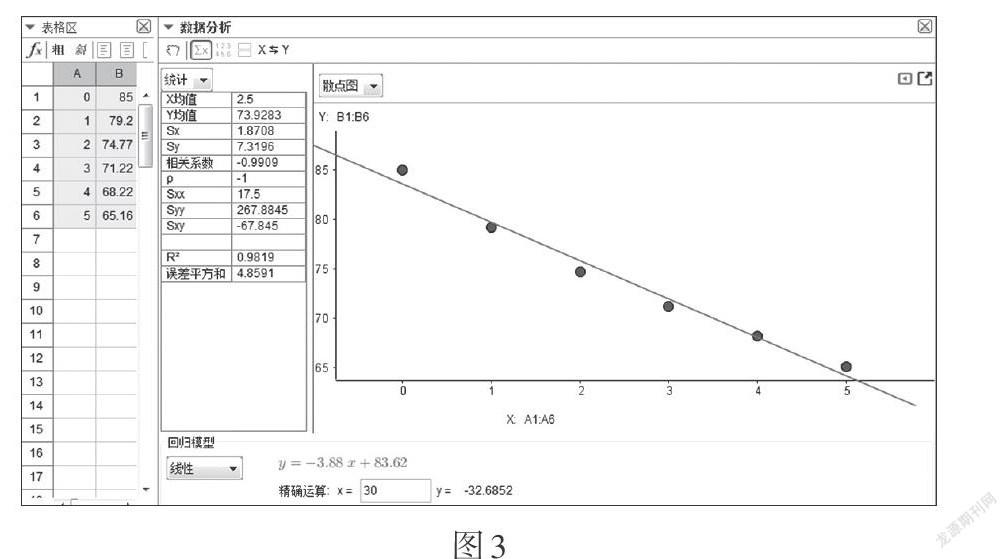
生1：我們組選擇一次函數(shù)，解析式為[y=-3.88x+][83.62]，從圖3看各點(diǎn)偏離較大，誤差平方和為4.859 1，相對較大，預(yù)測30分鐘之后的水溫為-32.685 2 ℃，與實(shí)際情況不符，我們組認(rèn)為一次函數(shù)模型擬合效果不夠理想.

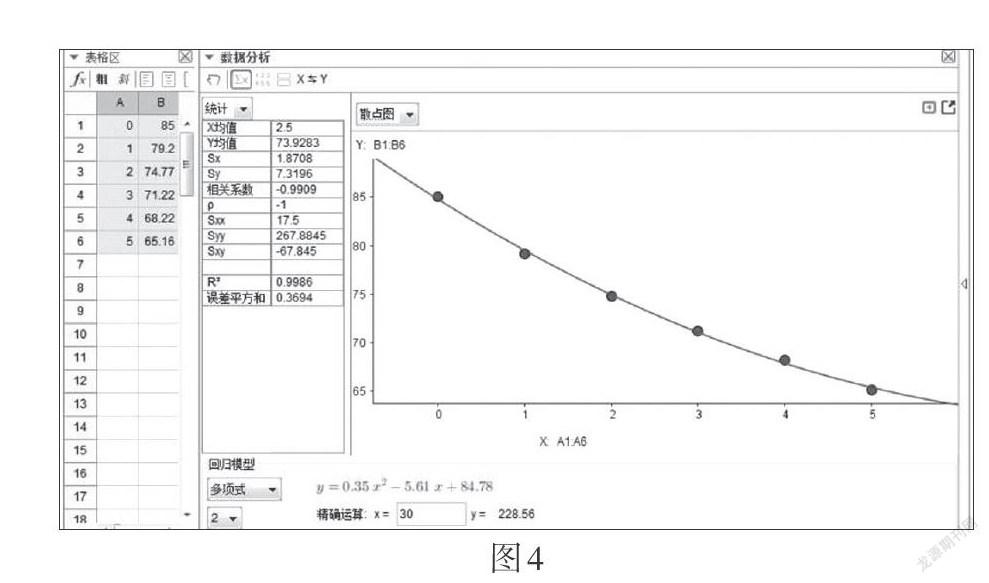
生2：我們組選擇了二次函數(shù)，解析式為[y=0.35x2-][5.61x+84.78]，從圖4來看各點(diǎn)基本都落在了曲線上，誤差平方和為0.369 4，相對較小，預(yù)測30分鐘后的水溫為228.56 ℃，與實(shí)際情況不符，我們組有些疑惑，這算不算一個好的函數(shù)模型呢？

師：誰能幫助生2解答這個問題？

生3：函數(shù)發(fā)展趨勢和實(shí)際不符的話就無法預(yù)測水溫什么時間降到60 ℃了.

師：很好！數(shù)學(xué)建模的目的是在對現(xiàn)有數(shù)據(jù)進(jìn)行函數(shù)模型擬合的基礎(chǔ)上，對數(shù)據(jù)未來的發(fā)展趨勢進(jìn)行預(yù)測，只在現(xiàn)有的數(shù)據(jù)范圍內(nèi)考慮不具有預(yù)測作用，也就失去了建模的意義.

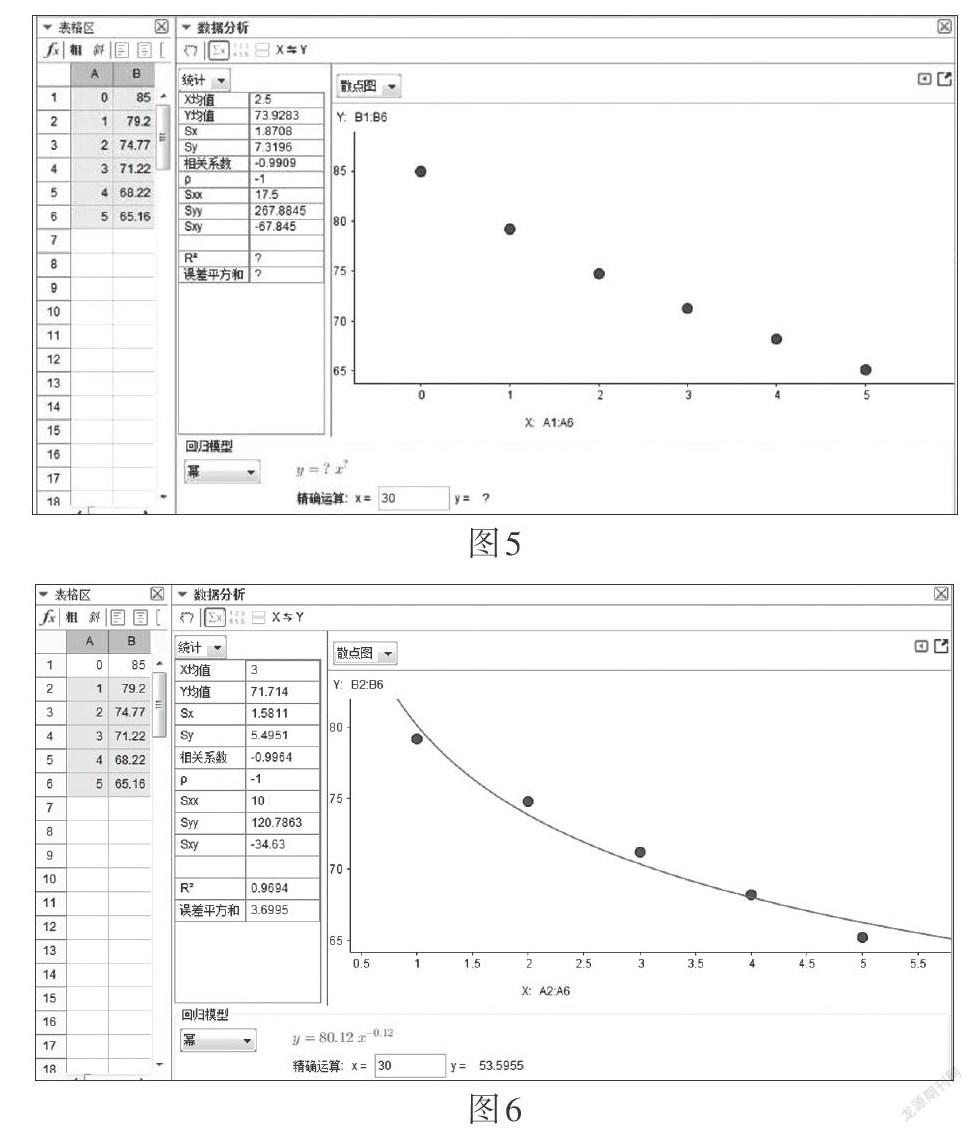
生4：我們組選擇了冪型函數(shù)，起初，根據(jù)圖5中的散點(diǎn)圖，我們并沒有得到函數(shù)圖象和解析式，分析原因是0不在定義域內(nèi)，所以我們選取了后面5個點(diǎn)進(jìn)行擬合，得到函數(shù)解析式[y=80.12x-0.12]. 從圖6來看各點(diǎn)都有偏離，誤差平方和為3.699 5，相對較大，預(yù)測30分鐘后的水溫為53.595 5 ℃，與前兩種模型相比，較為理想，我們組就想能否對這種模型進(jìn)行適當(dāng)?shù)馗倪M(jìn).

師：可以做哪些變化？

生4：當(dāng)[x]變大時，y會一直變小，直至逼近0，但實(shí)際上是逼近室溫的，所以函數(shù)圖象需要上移. 另外，圖象與y軸有交點(diǎn)，所以圖象需要左移，即在x的后面加[a a>0]，再考慮到形狀的變化，給出系數(shù)[k，] 我們認(rèn)為[y=kx+a+b a>0，b>0]是比較合適的.

師：生4所在的小組在經(jīng)歷一番挫折之后，注意到茶水溫度降到室溫就不能再降這一事實(shí)，結(jié)合散點(diǎn)圖的形狀及在坐標(biāo)系中的位置對函數(shù)模型進(jìn)行優(yōu)化，看來這個小組的合作非常充分，成員之間有思維的碰撞，產(chǎn)生了一些創(chuàng)造性的想法，值得肯定.

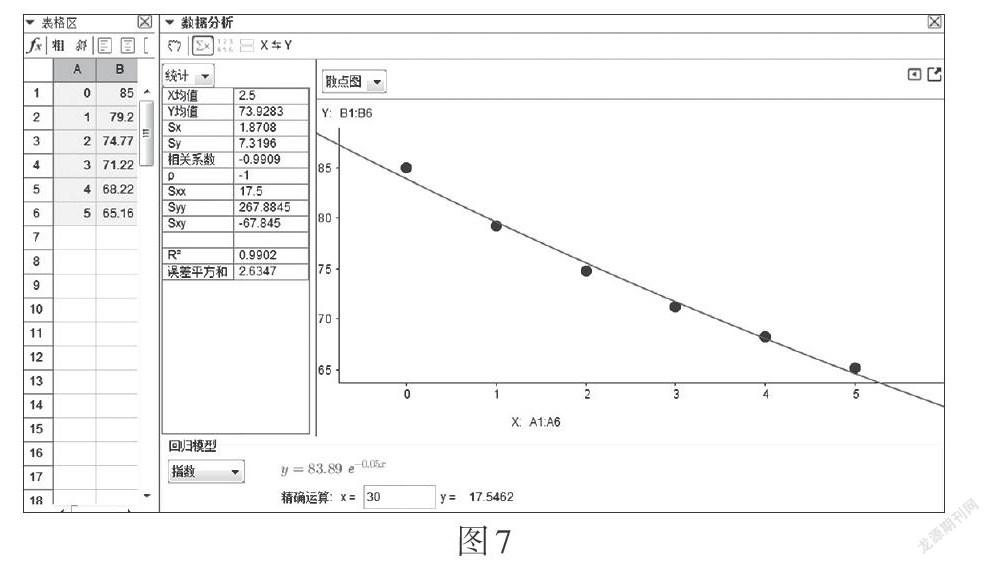
生5：我們組選擇了指數(shù)型函數(shù)，得到的解析式為[y=83.89e-0.05x]. 從圖7來看各點(diǎn)都有偏離，但偏離不大，誤差平方和為2.634 7，預(yù)測30分鐘后的水溫為17.546 2 ℃，借鑒生4所在小組的想法，我們組也對這種函數(shù)模型進(jìn)行了適當(dāng)優(yōu)化，得到[y=kax+b]，加b的理由與生4提出的一樣，考慮到圖象與y軸交點(diǎn)的縱坐標(biāo)為85及形狀的變化，添加系數(shù)[k].

【設(shè)計(jì)意圖】建立模型是本節(jié)課的重點(diǎn)，也是數(shù)學(xué)建模活動的關(guān)鍵環(huán)節(jié). 對此，以核心任務(wù)為驅(qū)動，為學(xué)生創(chuàng)造了實(shí)踐操作、探究發(fā)現(xiàn)、合作學(xué)習(xí)、個性展示、交流分享的機(jī)會. 鼓勵模型選擇的多樣化，使學(xué)生親身經(jīng)歷用數(shù)學(xué)軟件建立模型、檢驗(yàn)?zāi)Ｐ偷倪^程，強(qiáng)化了重點(diǎn)，提高了學(xué)生分析問題和解決問題的能力，學(xué)生的思維嚴(yán)謹(jǐn)性和思維能力也得到了有效提升.

（3）優(yōu)化模型，檢驗(yàn)?zāi)Ｐ停ㄖ攸c(diǎn)、難點(diǎn)）.

師：經(jīng)過剛才的篩選和優(yōu)化，大家認(rèn)為函數(shù)模型[y=kx+a+b]和[y=kax+b]的擬合效果哪個會更好？事實(shí)是否確實(shí)如此呢？

核心任務(wù)探究2：從函數(shù)模型[y=kx+a+b]和[y=][kax+b]中任選一個，小組合作完成以下任務(wù).

① 建立模型，求解模型.

② 分析誤差，檢驗(yàn)?zāi)Ｐ?

教師提供工具：計(jì)算機(jī).

要求：結(jié)果精確到0.01.

由小組推薦的代表進(jìn)行展示交流，其他小組進(jìn)行評價.

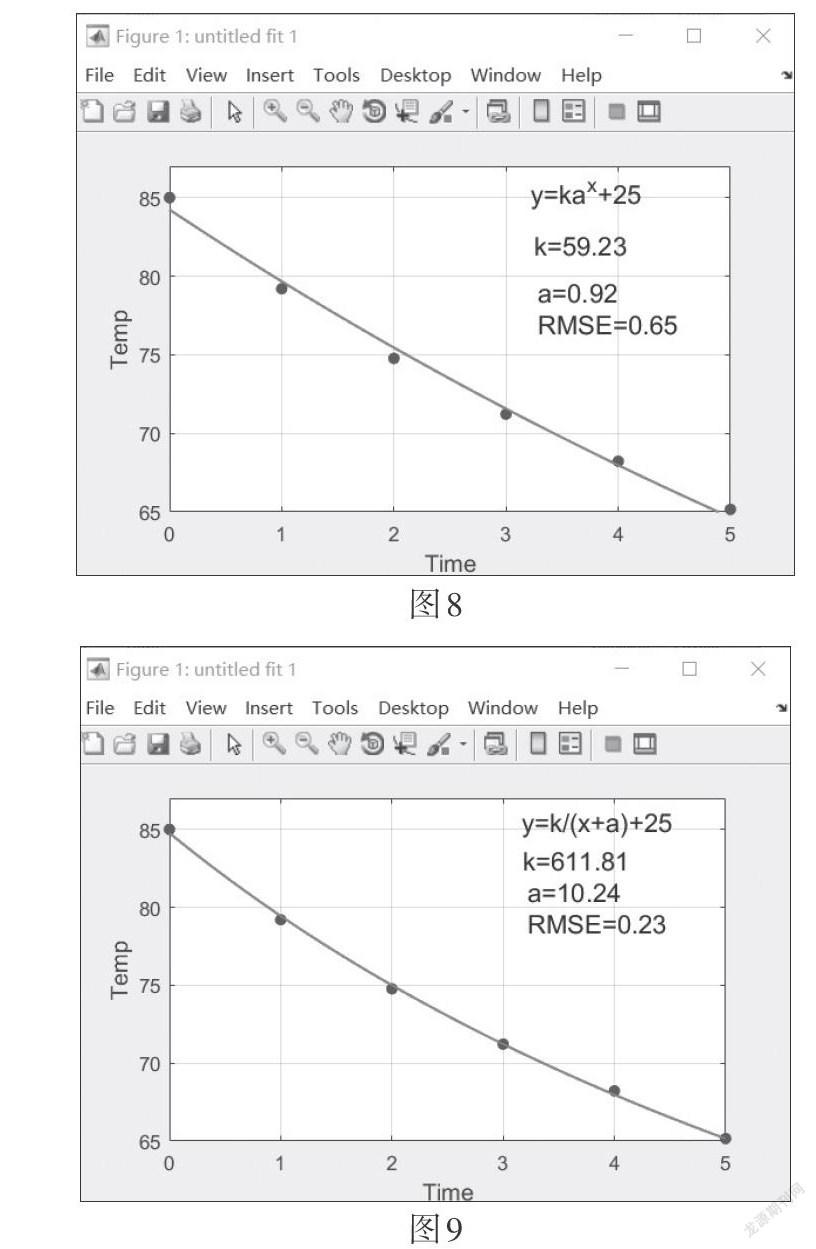
師生活動：由于現(xiàn)有的數(shù)學(xué)軟件中沒有這兩種函數(shù)模型，無法用現(xiàn)成的軟件來擬合. 學(xué)生主要用以下兩種方法來解決這個問題. 一是筆算的方式，用待定系數(shù)法求解，并通過計(jì)算殘差平方和進(jìn)行誤差分析;二是用MATLAB軟件編程建模. 在合作與交流的過程中，學(xué)生體會到通過有代表性的點(diǎn)的選取、精確的計(jì)算，以及對參數(shù)進(jìn)行適當(dāng)?shù)卣{(diào)整，對模型進(jìn)行不斷改進(jìn)可以達(dá)到更好的擬合效果. 此外，學(xué)生還給出了模型中參數(shù)的意義，揭示了數(shù)學(xué)模型與實(shí)際生活的聯(lián)系.

學(xué)生編程運(yùn)行的結(jié)果如圖8、圖9所示.

【設(shè)計(jì)意圖】該環(huán)節(jié)既是本節(jié)課的重點(diǎn)，也是難點(diǎn). 核心任務(wù)探究2給學(xué)生提供了多種工具，鼓勵建模方法的多樣化. 同時，讓學(xué)生體會用信息技術(shù)解決問題的優(yōu)越性. 通過合作探究、師生交流，學(xué)生對數(shù)學(xué)建模的一般方法及在建模過程中問題的解決有了更深刻的體會，進(jìn)一步強(qiáng)化了重點(diǎn)、突破了難點(diǎn)，也發(fā)展了學(xué)生的數(shù)學(xué)運(yùn)算、邏輯推理和數(shù)學(xué)建模素養(yǎng). 通過展示研究成果，小組之間相互評價、質(zhì)疑，分享心得和不足，學(xué)生的思維嚴(yán)謹(jǐn)性和語言表達(dá)能力得到了提升.

師：大家用數(shù)學(xué)軟件擬合出的函數(shù)，是用最小二乘法的原理得出的該種模型下的最優(yōu)函數(shù)，怎樣分析這兩種模型的優(yōu)劣呢？

核心任務(wù)探究3：比較以上兩種函數(shù)模型的擬合效果.

師生活動：通過集思廣益，學(xué)生想到可以比較殘差平方和的大小，這是從“數(shù)”的角度考慮，還有學(xué)生想到可以將函數(shù)圖象畫在同一坐標(biāo)系中，觀察圖象與數(shù)據(jù)的擬合程度，或者適當(dāng)增加數(shù)據(jù)點(diǎn)再進(jìn)行判斷，這是從“形”的角度考慮. 我們對學(xué)生的方法進(jìn)行一一驗(yàn)證，發(fā)現(xiàn)就現(xiàn)有數(shù)據(jù)點(diǎn)而言，冪型函數(shù)的擬合效果較好，但隨著后續(xù)數(shù)據(jù)的增多，指數(shù)型函數(shù)模型更接近實(shí)際.

【設(shè)計(jì)意圖】該探究活動的設(shè)置引導(dǎo)學(xué)生從數(shù)和形兩個角度來檢驗(yàn)?zāi)Ｐ停瑥?qiáng)調(diào)建模的結(jié)果要符合實(shí)際. 讓學(xué)生明確函數(shù)模型的擬合效果好是相對而言的，與數(shù)據(jù)點(diǎn)的選取有關(guān)，數(shù)學(xué)模型沒有最好只有更好，從而突破了本節(jié)課的又一難點(diǎn).

（4）聯(lián)系實(shí)際，解決問題.

師生活動：學(xué)生運(yùn)用模型計(jì)算出茶水冷卻到60 ℃所用的時間大致為7分鐘，這與實(shí)驗(yàn)測得的結(jié)果基本一致.

【設(shè)計(jì)意圖】建立數(shù)學(xué)模型的目的在于應(yīng)用模型解決實(shí)際問題，這是從數(shù)學(xué)問題到實(shí)際問題的轉(zhuǎn)化過程.通過解決實(shí)際問題，學(xué)生獲得將數(shù)學(xué)知識成功應(yīng)用于實(shí)踐的體驗(yàn). 至此，本節(jié)課的教學(xué)目標(biāo)也已達(dá)成.

（5）歸納小結(jié)，拓展提升.

師生活動：學(xué)生完善數(shù)學(xué)建模的流程圖，說說有哪些收獲和感想，隨后由教師補(bǔ)充完善，歸納概括數(shù)學(xué)建模的思想方法和基本步驟.

【設(shè)計(jì)意圖】在歸納、概括數(shù)學(xué)建模基本步驟和思想方法的同時獲得思維方式和價值觀的提升.

師生活動：作為知識的延伸和拓展，向?qū)W生展示牛頓冷卻模型.

【設(shè)計(jì)意圖】通過牛頓冷卻模型，讓學(xué)生體會科學(xué)家的探究歷程，激發(fā)學(xué)習(xí)動力.

3. 結(jié)題

師生活動：學(xué)生課后以小組為單位，完成“茶水最佳飲用時間”的研究報(bào)告，并且另選時間開展結(jié)題答辯.

【設(shè)計(jì)意圖】規(guī)范研究報(bào)告體例，讓學(xué)生將數(shù)學(xué)建模的過程以研究報(bào)告的形式呈現(xiàn)出來，并另選時間進(jìn)行報(bào)告、交流，讓學(xué)生分享成果和收獲. 教師組織學(xué)生進(jìn)行自評、互評，注重對學(xué)生數(shù)學(xué)建模活動的過程性評價.

參考文獻(xiàn)：

[1]中華人民共和國教育部制定. 普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）[M]. 北京：人民教育出版社，2018.

[2]章建躍，張艷嬌，金克勤. 數(shù)學(xué)建模活動的課程理解、教材設(shè)計(jì)與教學(xué)實(shí)施[J]. 中學(xué)數(shù)學(xué)教學(xué)參考（上旬），2020（5）：13-19.

[3]李現(xiàn)勇. 高中數(shù)學(xué)建模教學(xué)的實(shí)踐：以“學(xué)校無線信號發(fā)射器安裝方案”為例[J]. 數(shù)學(xué)通報(bào)，2020，59（1）：23-27.