文學(xué)作品中的邏輯推理在三視圖問(wèn)題中的應(yīng)用

徐歡眉

1引言

2004年開(kāi)始實(shí)施的《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（實(shí)驗(yàn)）》將“注重提高學(xué)生的數(shù)學(xué)思維能力”列為高中數(shù)學(xué)課程十大基本理念之一，《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》則將“直觀想象”和“邏輯推理”列入六大數(shù)學(xué)學(xué)科核心素養(yǎng)之中[1].直觀想象和邏輯推理（理論證明）貫穿數(shù)學(xué)學(xué)習(xí)的全過(guò)程，也是高考的重點(diǎn)考查方向.正如理性分析與感性認(rèn)知永遠(yuǎn)不是相互割裂的兩種能力，邏輯推理和直觀想象也能有機(jī)結(jié)合，小則提高數(shù)學(xué)思維與探究能力，大則更好地感知世界并與世界建立聯(lián)系.

如何將邏輯推理與直觀想象有機(jī)結(jié)合，本文將以《空間幾何體》中的三視圖問(wèn)題為例，利用著名文學(xué)作品《福爾摩斯探案集》中使用的邏輯，對(duì)三視圖問(wèn)題提出新的理解，實(shí)現(xiàn)邏輯推理與直觀想象的辯證統(tǒng)一.同時(shí)，在數(shù)學(xué)課堂中引入文學(xué)內(nèi)容，也是將文科和理科的有機(jī)結(jié)合，讓課堂更有活力，讓學(xué)生更有興趣.

2三視圖與文學(xué)作品中的邏輯推理

2.1空間幾何體的三視圖

在《2020年普通高等學(xué)校招生全國(guó)統(tǒng)一考試大綱》中對(duì)《空間幾何體》的要求是“認(rèn)識(shí)柱、錐、臺(tái)、球及其簡(jiǎn)單組合體的結(jié)構(gòu)特征，能畫(huà)出簡(jiǎn)單空間圖形（長(zhǎng)方體、球、圓柱、圓錐、棱柱等的簡(jiǎn)易組合）的三視圖，能識(shí)別上述的三視圖所表示的立體模型，了解球、棱柱、棱錐、臺(tái)的表面積和體積的計(jì)算公式”.在高考中，三視圖問(wèn)題的常見(jiàn)類型大致有以下兩種：

1.根據(jù)三視圖還原幾何體的形狀，并求解幾何體的表面積和體積;

2.根據(jù)幾何體的部分視圖求剩余部分視圖.[2]

空間幾何體是學(xué)生第一次系統(tǒng)地接觸三維空間.在此之前，他們?cè)诔踔须A段獲得了二維空間的知識(shí)，對(duì)三維空間無(wú)限性和復(fù)雜性的認(rèn)知十分有限，從平面圖形到空間幾何體的遷移對(duì)部分空間想象力薄弱的學(xué)生而言并非易事.

空間想象力是對(duì)客觀事物空間形式的抽象思維能力[3]，對(duì)應(yīng)數(shù)學(xué)學(xué)科核心素養(yǎng)中的直觀想象.空間中圖形的位置關(guān)系，立體圖形的疊加與切割，都需要學(xué)生在大腦中建立起三維模型，而三視圖問(wèn)題則是對(duì)這種能力的綜合考查，學(xué)生需要掌握平行投影和中心投影，學(xué)會(huì)在平面中表示空間圖形的技能[4].

2.2文學(xué)作品中的邏輯推理

“當(dāng)你排除所有不可能的部分，剩下的無(wú)論多么不可能，也一定是真相.”[5]這句名言出自柯南·道爾著名中篇小說(shuō)《四簽名》，其筆下的名偵探夏洛克·福爾摩斯常用此邏輯將案件解決.推理小說(shuō)中就運(yùn)用了大量的感性認(rèn)知與理性分析，分別對(duì)應(yīng)看得見(jiàn)的線索和看不見(jiàn)的推理.構(gòu)成福爾摩斯演繹法的兩大核心要素——觀察與推理.觀察是對(duì)線索的捕獲、對(duì)有效信息的發(fā)現(xiàn)，放在數(shù)學(xué)問(wèn)題中即對(duì)題目信息的獲取與翻譯;推理包括兩大基本過(guò)程——?dú)w納推理和演繹推理.

記結(jié)論的全集為，滿足條件的結(jié)論用集合表示，不滿足條件的結(jié)論用集合表示，顯然， .上述引文背后的數(shù)學(xué)知識(shí)，即排除全集U中不滿足條件的結(jié)論，剩下的就是集合B的補(bǔ)集，即集合A，也就是滿足條件的結(jié)論.關(guān)鍵詞為“所有”，只有所有不滿足條件的結(jié)論構(gòu)成的集合才能與滿足條件的結(jié)論構(gòu)成的集合互為補(bǔ)集.通過(guò)排除所有不滿足條件的結(jié)論，我們就能得到滿足條件的結(jié)論.

這種方式主要針對(duì)根據(jù)已知條件很難直接得出結(jié)論的一類問(wèn)題——沒(méi)有很好的空間想象力，很難通過(guò)三視圖直接作出幾何體的直觀圖;而根據(jù)已知條件，排除掉一些結(jié)論會(huì)比較容易——以某個(gè)基本幾何體作為參照，根據(jù)三視圖排除該參照物中肯定不存在于所求幾何體上的頂點(diǎn)或棱，“排除所有不可能的”，關(guān)注“剩下的”，最終就能得到“真相”.這種方式結(jié)合了從三視圖中獲得的感性認(rèn)知與推理過(guò)程中的理性分析，是直觀想象與邏輯推理的有機(jī)結(jié)合.

3例題分析

3.1根據(jù)三視圖還原簡(jiǎn)單幾何體

3.1.1三視圖中無(wú)虛線

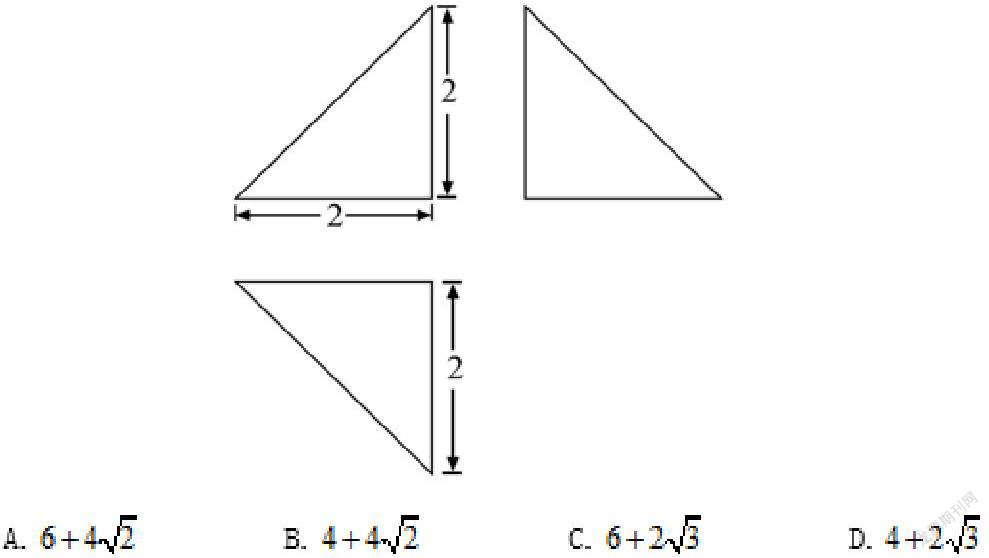
例1（2020年高考全國(guó)卷理科III卷第8題）下圖為某幾何體的三視圖，則該幾何體的表面積是（）

在該題中，由于三個(gè)視圖均為三角形，結(jié)合空間幾何體的結(jié)構(gòu)特征的相關(guān)知識(shí)，空間想象力好的學(xué)生可以直接判斷出該幾何體為三棱錐并畫(huà)出其直觀圖，進(jìn)而求得該三棱錐的各條棱長(zhǎng)及其表面積.倘若學(xué)生無(wú)法在大腦中建立起該幾何體的三維模型，我們能否利用本文2.2中講述的邏輯點(diǎn)，推理出該幾何體原本的形狀呢？

結(jié)合三視圖“長(zhǎng)對(duì)正，高平齊，寬相等”的原則，我們必能得到該幾何體恰好能被放置在棱長(zhǎng)為2的立方體中（圖3-1），且該幾何體的頂點(diǎn)均為此立方體的頂點(diǎn)，至于是哪些頂點(diǎn)構(gòu)成了該幾何體，我們“排除一切不可能的”，關(guān)注“剩下的”，看看是否與“真相”接近.

若規(guī)定垂直于平面為主視方向，首先，根據(jù)主視圖可以判斷，立方體中的頂點(diǎn)和不存在于該幾何體中;同理，根據(jù)側(cè)視圖可以判斷，頂點(diǎn)也不是該幾何體的頂點(diǎn);最后，由俯視圖可知，頂點(diǎn)A也不存在于該幾何體中，將“不可能的”點(diǎn)去掉，將“剩下的”點(diǎn)連接起來(lái)（圖3-2），得到三棱錐，經(jīng)檢驗(yàn)發(fā)現(xiàn)，符合題干中的三視圖.

除此之外，還可通過(guò)另一種方式判斷剩余四個(gè)頂點(diǎn)確實(shí)是該幾何體的頂點(diǎn).由主視圖和側(cè)視圖可知，棱和（不含端點(diǎn)）均不在該幾何體中，為了滿足主視圖中位于上方的三角形頂點(diǎn)存在，則立方體中的頂點(diǎn)必然存在，同理可推理出其余三個(gè)頂點(diǎn)也必然存在.

3.1.2三視圖中有虛線

根據(jù)有虛線的三視圖還原幾何體一直是學(xué)生不知從何入手的一類問(wèn)題，對(duì)空間想象力的要求更高，往往信息量越大，題目越復(fù)雜.原則是看得見(jiàn)的線用實(shí)線，看不見(jiàn)的線用虛線.但即便知道這一原則，多數(shù)學(xué)生也不知該如何利用.如果無(wú)法想象出幾何體的形狀，我們依然可以試試邏輯推理的方法.

例2下圖為某多面體的三視圖，則該多面體的體積為_(kāi)_______.

易知該幾何體必能被放置在棱長(zhǎng)為4的立方體中（圖3-1），如上一個(gè)例子，我們首先排除不可能的點(diǎn).根據(jù)主視圖和俯視圖可以排除頂點(diǎn).同時(shí)可排除棱（不含端點(diǎn)）（圖3-3）.在剩下的頂點(diǎn)中，我們可以通過(guò)同例1相似的推理，得到必然是該幾何體的頂點(diǎn)，否則無(wú)法滿足三視圖.剩下暫時(shí)無(wú)法判斷的頂點(diǎn)D，再看信息量最大的側(cè)視圖.根據(jù)“看得見(jiàn)的用實(shí)線”這一原則，若頂點(diǎn)D是該幾何體的頂點(diǎn)，那么四邊形是側(cè)視圖中能被看到的圖形，也就意味著題干中側(cè)視圖的實(shí)對(duì)角線將無(wú)法體現(xiàn)，因此頂點(diǎn)D不是該幾何體的頂點(diǎn).至此，我們已排除了所有不可能的頂點(diǎn)，僅剩，這四點(diǎn)構(gòu)成的三棱柱經(jīng)檢驗(yàn)滿足題目條件（圖3-4）.我們發(fā)現(xiàn)，利用邏輯推理得到幾何體的過(guò)程中，側(cè)視圖中虛線的信息僅在檢驗(yàn)時(shí)用到，大大降低了難度.

3.2根據(jù)三視圖還原組合體

空間中的組合體有疊加式、切割式和綜合式三種基本形式.疊加式組合體由多個(gè)基本幾何體疊加而成，按照幾何體之間接觸方式的不同，可細(xì)分為相接、相切、相貫三種類型.切割式組合體可視為在基本幾何體上進(jìn)行切割、鉆孔、挖槽后剩余部分所形成的幾何體.綜合式組合體為多個(gè)基本幾何體的疊加及切割，是組合體中最為常見(jiàn)的形式.

疊加式和切割式在高考中考查得比較多，其中疊加式組合體為中低難度，考生能夠根據(jù)三視圖較為容易地判斷出構(gòu)成組合體的基本幾何體的類型，進(jìn)而還原出組合體的形狀，判斷幾何特征，求解表面積與體積.切割式組合體對(duì)考生的空間想象能力要求更高，需要利用三視圖中虛線實(shí)線的特征，判斷出該幾何體是對(duì)何種基本幾何體做了怎樣的切割，進(jìn)而還原出組合體的形狀.它與疊加式組合體不同的是，我們能從疊加式組合體的三視圖中迅速辨認(rèn)出常見(jiàn)的基本幾何體，而切割式組合體的三視圖無(wú)法給我們直觀的信息，在運(yùn)用空間想象力的同時(shí)還需要一定的邏輯推理.

3.2.1疊加式組合體

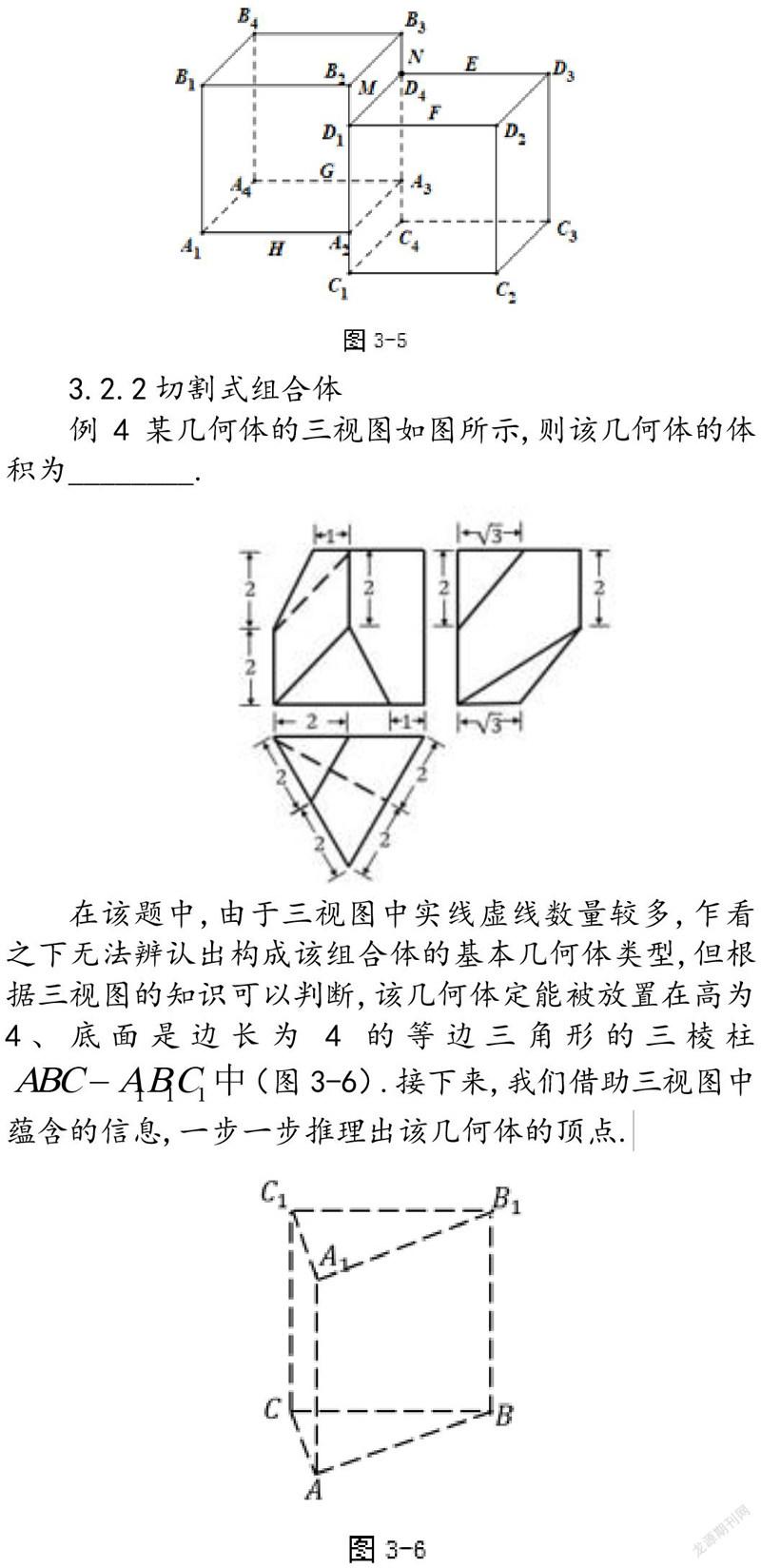
例3（2020年高考全國(guó)卷理科II卷第7題）如圖是一個(gè)多面體的三視圖，這個(gè)多面體某條棱的一個(gè)端點(diǎn)在正視圖中對(duì)應(yīng)的點(diǎn)為M，在俯視圖中對(duì)應(yīng)的點(diǎn)為，則該端點(diǎn)在側(cè)視圖中對(duì)應(yīng)的點(diǎn)為（ ）

不難發(fā)現(xiàn)，在該題中，組成三視圖的基本幾何圖形為矩形，由此可辨別出該幾何體由兩個(gè)四棱柱相接而成，此幾何體為疊加式組合體.需要注意的是，在疊加式組合體中，若分處兩個(gè)幾何體的兩個(gè)平面共面，則相接部分的棱在三視圖中無(wú)法體現(xiàn)（對(duì)應(yīng)主視圖內(nèi)部并無(wú)實(shí)線）.而側(cè)視圖中的實(shí)線與虛線則告訴我們兩個(gè)四棱柱的相對(duì)位置，進(jìn)而得到還原后的幾何體（圖3-5）.因此答案為A.

3.2.2切割式組合體

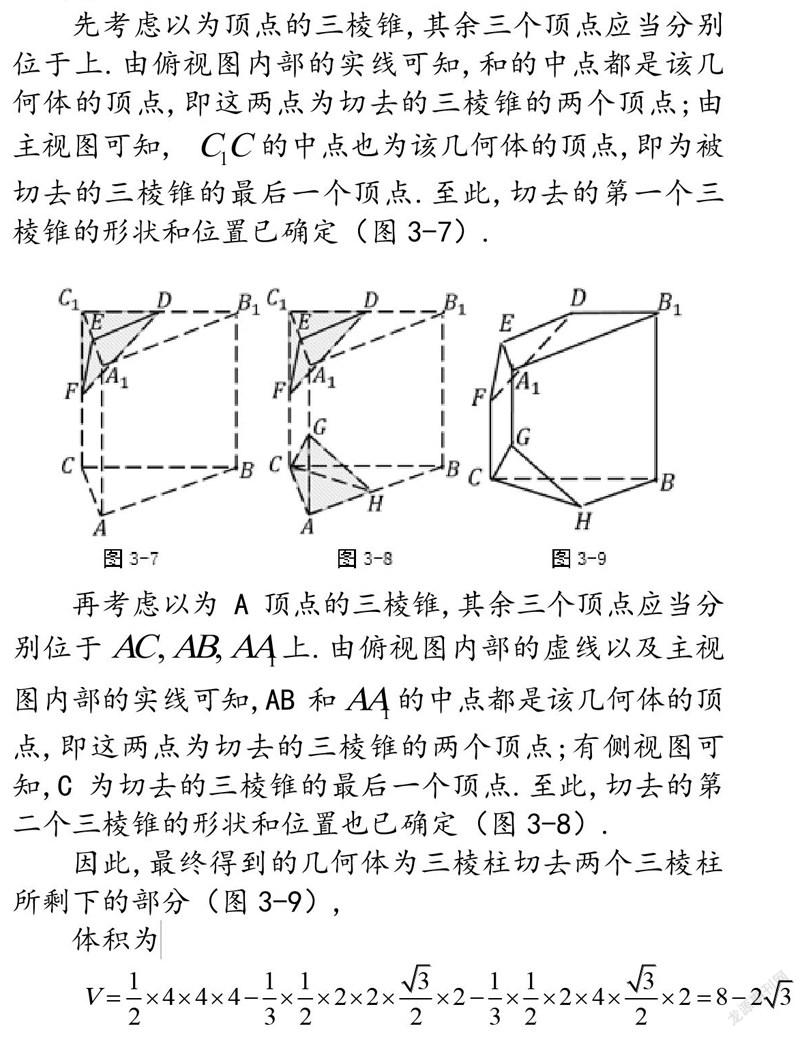
例4某幾何體的三視圖如圖所示，則該幾何體的體積為_(kāi)_______.

在該題中，由于三視圖中實(shí)線虛線數(shù)量較多，乍看之下無(wú)法辨認(rèn)出構(gòu)成該組合體的基本幾何體類型，但根據(jù)三視圖的知識(shí)可以判斷，該幾何體定能被放置在高為4、底面是邊長(zhǎng)為4的等邊三角形的三棱柱中（圖3-6）.接下來(lái)，我們借助三視圖中蘊(yùn)含的信息，一步一步推理出該幾何體的頂點(diǎn).

首先，根據(jù)主視圖外部圖形可視為矩形切去左上角以及俯視圖內(nèi)部實(shí)線可知，三棱柱中的頂點(diǎn)不存在于該幾何體中;其次，根據(jù)側(cè)視圖外部圖形可視為矩形切去右下角以及俯視圖內(nèi)部虛線可知，三棱柱中的頂點(diǎn)A不存在與該幾何體中.而其余四個(gè)頂點(diǎn)均可推理得出存在于該幾何體中.

“排除一切不可能的，關(guān)注剩下的部分”.從整體上看，所求的幾何體應(yīng)為三棱柱切去分別以A和為頂點(diǎn)的兩個(gè)三棱錐.至于兩個(gè)三棱錐中其余三個(gè)頂點(diǎn)位于三棱柱的什么位置，我們?cè)偻ㄟ^(guò)三視圖中的實(shí)線和虛線加以判斷.

先考慮以為頂點(diǎn)的三棱錐，其余三個(gè)頂點(diǎn)應(yīng)當(dāng)分別位于上.由俯視圖內(nèi)部的實(shí)線可知，和的中點(diǎn)都是該幾何體的頂點(diǎn)，即這兩點(diǎn)為切去的三棱錐的兩個(gè)頂點(diǎn);由主視圖可知， 的中點(diǎn)也為該幾何體的頂點(diǎn)，即為被切去的三棱錐的最后一個(gè)頂點(diǎn).至此，切去的第一個(gè)三棱錐的形狀和位置已確定（圖3-7）.

再考慮以為A頂點(diǎn)的三棱錐，其余三個(gè)頂點(diǎn)應(yīng)當(dāng)分別位于上.由俯視圖內(nèi)部的虛線以及主視圖內(nèi)部的實(shí)線可知，AB和的中點(diǎn)都是該幾何體的頂點(diǎn)，即這兩點(diǎn)為切去的三棱錐的兩個(gè)頂點(diǎn);有側(cè)視圖可知，C為切去的三棱錐的最后一個(gè)頂點(diǎn).至此，切去的第二個(gè)三棱錐的形狀和位置也已確定（圖3-8）.

因此，最終得到的幾何體為三棱柱切去兩個(gè)三棱柱所剩下的部分（圖3-9），體積為

4結(jié)語(yǔ)

世間萬(wàn)物緊密聯(lián)系，我們想知道某件事物的本質(zhì)，未必只能通過(guò)研究該事物，還可通過(guò)了解與其相關(guān)聯(lián)的一切事物來(lái)探尋它的本質(zhì).知識(shí)結(jié)構(gòu)是網(wǎng)狀的，知識(shí)正遷移是快速掌握新知識(shí)的有效途徑.而在知識(shí)遷移的過(guò)程中，也要充分利用核心素養(yǎng)之間的聯(lián)系.

我們身處的世界充滿了可探尋的事物，需要我們?nèi)ビ^察，去推理.要善于發(fā)現(xiàn)并利用事物之間的聯(lián)系，建立起感性認(rèn)知與理性分析之間的橋梁.

正如柯南·道爾在小說(shuō)《五個(gè)橘核》中所說(shuō)，“因世間的一切就像根鏈條，我們只需瞧見(jiàn)其中一環(huán)，就可知全體的性質(zhì)”

（作者單位：杭州市余杭區(qū)杭州英特外國(guó)語(yǔ)學(xué)校）