基于探鳥雷達的機場周邊鳥類目標數量估計

陳唯實 黃毅峰 盧賢鋒 張潔 陳小龍

(1. 中國民航科學技術研究院, 北京 100028; 2. 海軍航空大學, 煙臺 264001)

鳥擊航空器是民航的傳統安全隱患[1]。 全球每年約發生21 000 起鳥擊事件,造成經濟損失約12 億美元[2]。 2009 年1 月15 日發生的全美航空公司1549 號航班哈德遜河緊急迫降事件,是迄今為止最為典型的一起鳥擊事故[3]。 隨著航班量的持續增長和生態環境的不斷改善,中國機場的鳥擊防范工作壓力持續增大。 2019 年,全國運輸機場共發生責任區鳥擊事件836 起,同比增加113 起,增幅15.6%,責任區鳥擊事件萬架次率為0.72,增幅10%。

《運輸機場運行安全管理規定》[4]要求機場管理機構應持續開展鳥害防范基礎性調研,全面掌握機場內及其附近地區的生態環境、鳥類種群、數量、位置分布及活動規律;繪制鳥類活動平面圖;掌握機場內及其附近地區與鳥情動態密切相關的生物類群及影響因素的時間、空間分布情況,分析其中的關系;據此制定和不斷完善鳥害防范實施方案,確定各階段應當重點防范的對象,有針對性地實施鳥害防范措施。

近年來,探鳥雷達技術取得了長足進步,其作為鳥情觀測的重要技術手段,能夠全天候自動運行并持續積累飛鳥目標雷達數據[5]。 通過對探鳥雷達數據的處理分析,有助于掌握機場周邊鳥類活動規律,及時形成鳥情分析報告,指導機場制定科學合理的鳥防措施[6]。 相比之下,傳統的機場鳥情生態環境主要依靠人工并借助望遠鏡和夜視儀完成,調研方法主要包括樣帶法、樣點法和計數鳥群法,且要求調研人員具備鳥類學專業知識[7]。 因此,機場通常會聘請專業的鳥情生態環境調研機構開展相關工作,周期一般為5 年一次?？梢?傳統的鳥情生態環境調研方法雖然能夠識別鳥種,但效率較低、實時性不強,機場管理機構難以及時掌握機場周邊最新的鳥情態勢,從而制定可實時調整的有針對性的應對策略。 利用先進的探鳥雷達技術,結合人工鳥情調研方法,成為機場鳥情觀測的發展趨勢。

針對以上需求,本文提出了一種基于探鳥雷達數據的機場周邊鳥類目標數量估計方法,采用多目標航跡自動起始跟蹤算法對探鳥雷達獲取的飛鳥目標信息進行處理分析,實時估計熱點區域內的鳥類目標數量,幫助機場管理機構及時掌握機場周邊的鳥類數量變化情況及分布態勢。

1 探鳥雷達

目前,國內外已經研制出了相對成熟的機場探鳥雷達系統。 其中,國外最具代表性的產品包括美國的Merlin 雷達、加拿大的Accipiter 雷達、荷蘭的Robin 雷達及英國的Aveillant 雷達,國內的部分高校和科研院所也開展了探鳥雷達技術研究,探鳥效果逐步提升[8]。

圖1 為典型的雙天線機場探鳥雷達系統(https://detect-inc. com/)。 其通常配有2 部不同波段的雷達,一部為X 波段垂直掃描雷達,另一部為S 波段水平掃描雷達,均采用T 型波導陣列天線,大部分早期成熟的探鳥雷達均采用這種體制,如Merlin、Accipiter 和Robin。 水平掃描雷達能覆蓋機場周邊的廣大地區,并獲取水平平面的二維信息,但不能提供高度信息;垂直掃描雷達可以獲得垂直平面的高度信息。 由于水平和垂直掃描的2 部雷達覆蓋的范圍不同,波束重疊區域很小,系統獲得的三維信息不是真正的三維。 探鳥雷達系統通常被放置在機場跑道的附近或一端,對包括航班起降通道在內的機場區域進行監控。 垂直掃描雷達與跑道連成一線,使其掃描范圍恰好覆蓋航班的起降通道,同時提供該區域的鳥類目標高度信息;水平掃描雷達對機場周邊區域進行掃描,對進入該區域的鳥類目標進行預警。 對于小型鳥類,該系統的探測范圍可以達到垂直高度2 300 m,水平距離2 ～3 n mile(1 n mile =1.852 km);對于中大型鳥類或鳥群,探測范圍可以達到垂直高度15 000 ft(1 ft =0.304 8 m),水平距離為4 ～6 n mile。近年來,以Aveillant 雷達系統為代表的相控陣、全息雷達等先進的雷達技術逐步應用于機場探鳥,進一步提高了鳥情數據的可靠性,引領了探鳥雷達技術的發展方向。

圖1 典型的雙天線機場探鳥雷達系統Fig.1 Typical airport avian radar system with dual antennas

2 多目標航跡自動起始跟蹤

雷達獲得的量測數據包括目標信息及部分雜波干擾,跟蹤目的在于從雜波中提取出每個目標形成的航跡。 目標跟蹤要先解決目標狀態的初始化關聯,即航跡起始問題[9]。 現有的航跡起始跟蹤算法主要包括順序處理和批處理兩大類[10]。順序處理算法通?；谝欢ǖ倪壿嬕巹t,主要包括直觀法[11]和邏輯法[12],此類算法計算量較小,但在雜波環境中性能下降明顯。 批處理算法主要包括Hough 變換法及其衍生的改進算法[13-14],此類算法發源于圖像處理,可以起始直線運動的目標且適用于雜波環境,但由于計算量較大導致航跡起始的實時性欠佳。 近年來,支持向量機[15]、隨機森林[16]、神經網絡[17]等智能算法也被用于航跡起始,但此類算法通常只適用于特定的訓練數據,普遍存在可移植性差和時效性不佳的問題。

針對以上問題,本文結合機場鳥類活動規律,基于探鳥雷達獲取的鳥情數據,以鳥類目標活動熱點為參照點,建立飛鳥目標航跡起始與消亡的概率分布模型,縮短了航跡起始時間,降低了航跡虛警率。 本節首先介紹多目標航跡自動起始跟蹤的算法流程,進而討論多目標數據關聯算法、目標生命周期中各類可能事件的關聯概率估計及卡爾曼濾波與平滑方法。

2.1 算法流程

多目標航跡自動起始跟蹤算法的關鍵和難點在于目標狀態的初始化。 基于當前時刻的狀態預估值,由粒子濾波的數據關聯算法對當前時刻的量測值與可能事件一一關聯,包括目標的新生、延續和消亡,同時排除雜波影響。 在量測值與所有已知目標的預估狀態和新生目標的初始狀態關聯之后,進行卡爾曼狀態更新,獲得當前存在的所有目標的狀態更新值。 對全部卡爾曼濾波結果進行平滑處理,得到每個存在過的目標的平滑航跡。算法流程如圖2 所示。

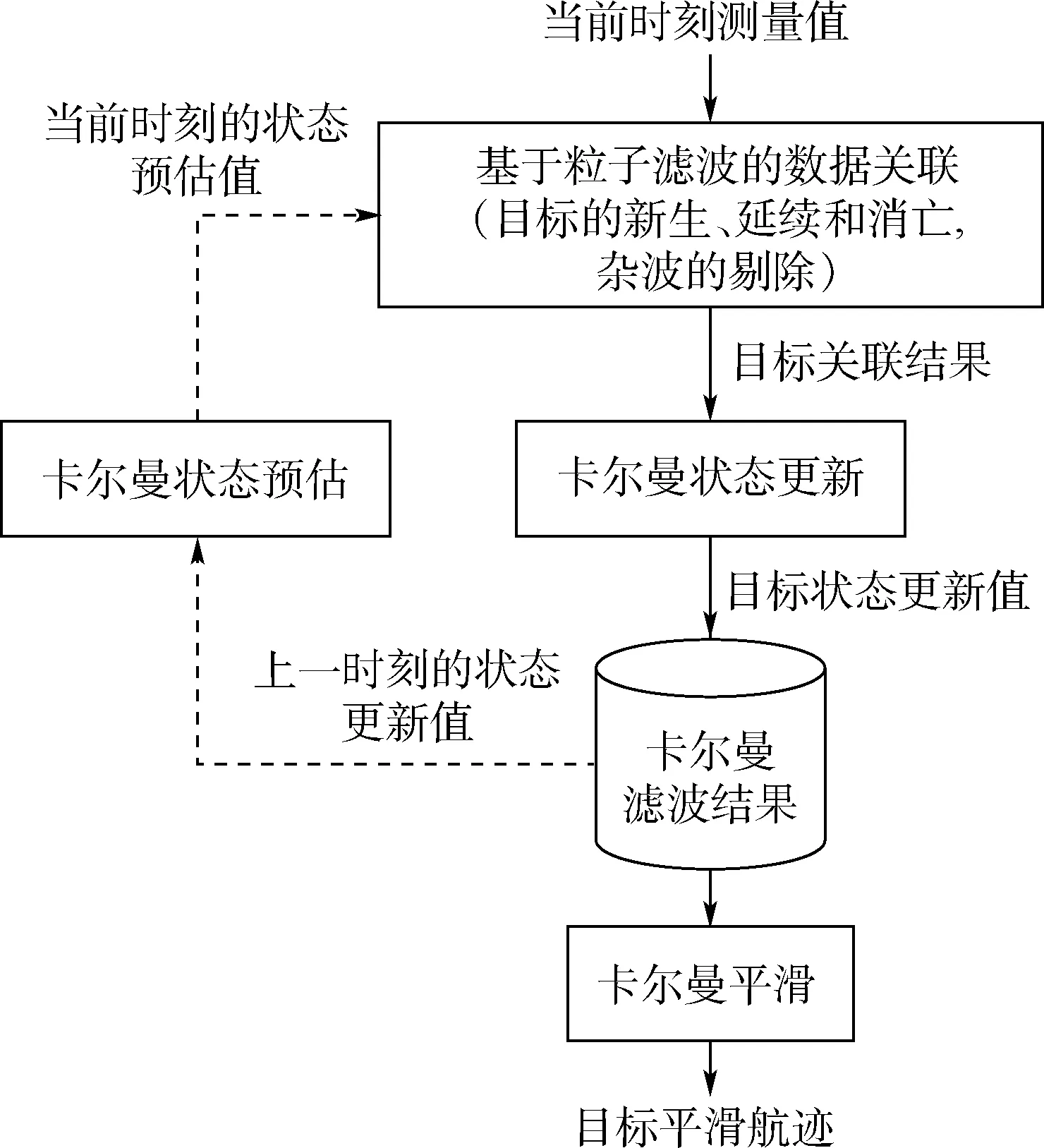
圖2 多目標航跡自動起始跟蹤算法流程Fig.2 Flowchart of multi-target automatic initiation and tracking algorithm

每個目標都有其生命周期,即從新生到消亡的過程,因此目標存在的數目始終處于變化之中。通過數據關聯算法,判斷量測屬于已存在的目標、新生目標、抑或雜波,從而將復雜的雷達多目標跟蹤問題簡化為普通的單目標跟蹤問題,同時記錄每個目標的生命周期,對當前存在的目標總數進行實時統計。

2.2 數據關聯算法

基于粒子濾波算法進行的多目標數據關聯,可視為多假設跟蹤(Multiple Hypothesis Tracking,MHT)算法的推廣。 每個粒子代表不同的數據關聯假設,降低了MHT 算法的復雜性。 在每個粒子中,將量測與若干可能事件相關聯,計算每個事件的先驗概率Pp和事件關聯相似度Pl,進而給出每個事件的關聯概率P,2.3 節將列出所有可能事件的關聯概率模型。

估計有效樣本數目ne,且

如果ne過小,則進行重采樣。

2.3 可能事件關聯概率估計

在沒有任何先驗知識的情況下,量測的關聯結果需要基于對雜波、新生目標、已知目標、目標消亡等所有可能事件出現概率的計算。

設pb為航跡起始即新生目標概率,新目標的出現意味著當前量測作為新目標的起始狀態。 本文中,將飛鳥目標活動熱點作為目標航跡起始的參考點,通過量測與熱點的關聯度起始航跡,降低了跟蹤算法的復雜性,并提高了其效率與工程適用性。 另外,設pd為目標消亡概率,以gamma 分布建模:

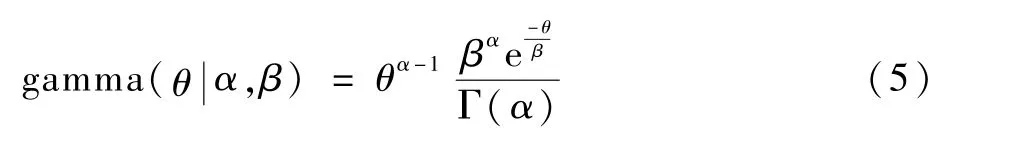
式中:θ為目標航跡與量測關聯的中斷時間,中斷時間越長,目標消亡的概率越大;函數的坡度隨α和β的不同取值而變化。

因此,建立所有可能的量測關聯事件概率模型,并歸納如下:

1) 雜波,無目標消亡。

5) 新目標航跡起始,無目標消亡。

基于以上6 類可能事件的關聯概率估計結果,實現對每個目標從新生、延續直至消亡的全生命周期管理。

2.4 卡爾曼濾波與平滑

卡爾曼濾波的實質在于:根據目標的當前狀態估計其未來的狀態,并通過量測值對其進行修正。 卡爾曼濾波分為2 步:①預估。 根據前一步的量測值預估出系統下一步的狀態。 ②更新。 根據當前時刻的量測值估計出系統的當前狀態。 其中,預估部分由方程(13)完成:

式中:mk和Pk分別為k時刻獲得量測之后估計的狀態均值和方差;v為量測修正;K為濾波增益,其定義了預估值修正的程度。

卡爾曼平滑與卡爾曼濾波的流程類似,區別在于濾波的遞推是前向的,而平滑的遞推是后向的。 經過卡爾曼平滑的處理,可以獲得比僅進行卡爾曼濾波更高的精度。

3 仿真數據分析

本節針對不同雜波環境中的目標跟蹤仿真數據,通過蒙特卡羅實驗,評價本文算法特別是多目標航跡自動起始跟蹤算法的有效性,重點在于不同參數設置情況下目標航跡起始的及時性及目標數目的變化情況。

3.1 目標航跡起始仿真

運動目標狀態表示為

式中:(xk,yk)為二維直角坐標系中目標在k時刻的位置;(?xk,?yk)為速度。

目標的離散動態模型可以表示為線性、時不變構造方程:

其中:時間步長設定為Δt=0.01,過程噪聲的功率譜密度設定為q=0.001。

圖3 為雜波環境中目標的仿真航跡,仿真步數為50 步。 量測中屬于目標的部分附加了一定的高斯噪聲,雜波均勻地分布在[ -5,5] ×[ -1,9]的區域內,其在每個掃瞄周期中出現的數量滿足均值為λ的泊松分布。 以(0,0)為目標起始的參考點,目標航跡的起始點與參考點的距離為d,目標起始速度的絕對值為1,起始方向在0° ～360°范圍內隨機分布。 圖3 為某次仿真實驗的目標航跡示意圖,圖3(a)為全局示意圖,圖3(b)為局部放大圖,該實驗中d=0.2,λ=0.5,且粒子數N=50。

圖4 為另一次仿真實驗的目標航跡示意圖,圖4(a)為全局示意圖,圖4(b)為局部放大圖,該實驗中d= 3,λ= 1,且粒子數N= 50。 對比圖3和圖4 的2 次目標跟蹤結果可知,圖3 中的目標航跡起點距參考點很近(d=0. 2),航跡起始沒有延時;圖4 中的目標航跡起點距參考點相對較遠(d=3),航跡起始出現了1 個周期的延遲。

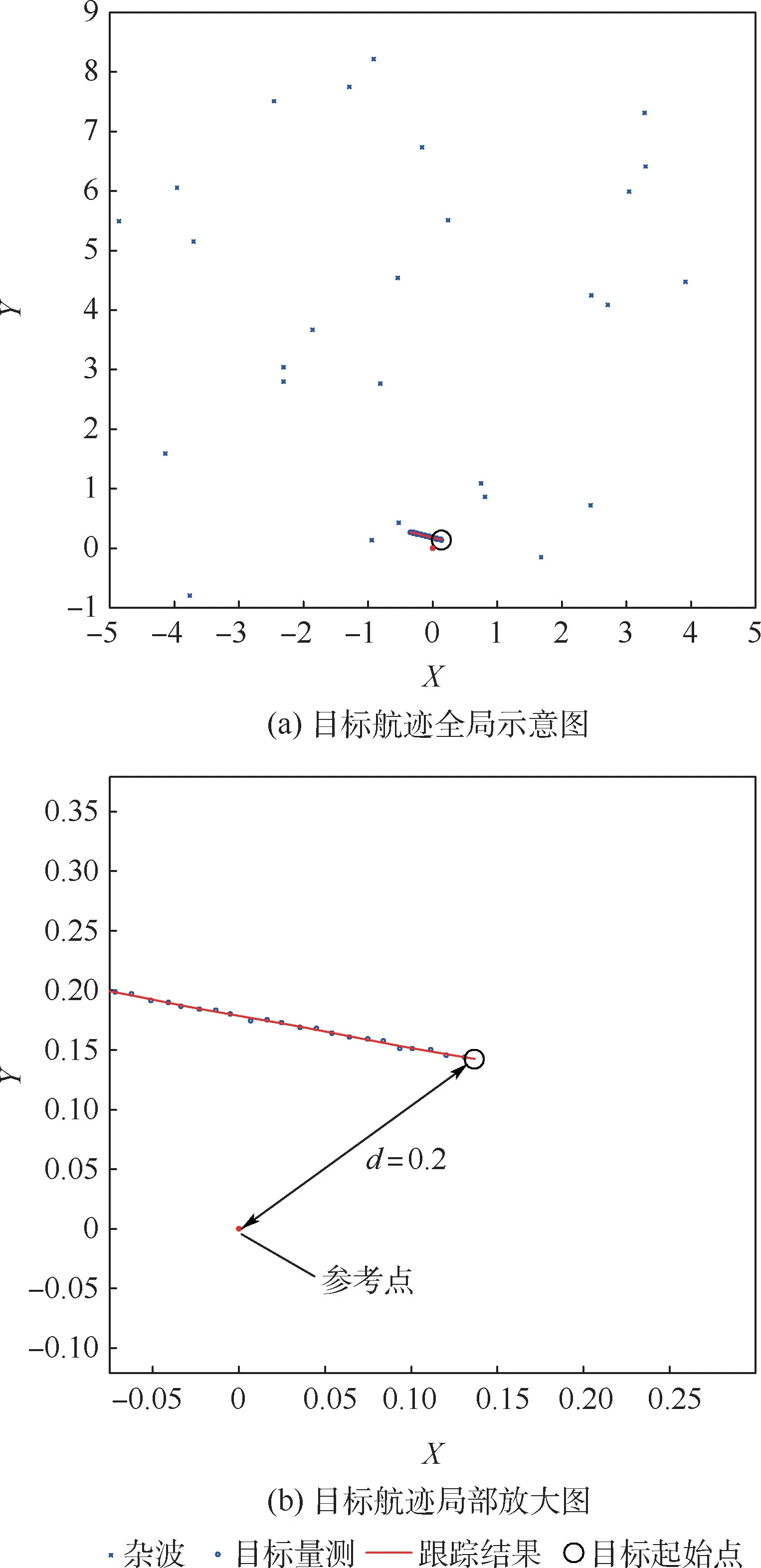
圖3 無延遲起始的目標跟蹤起始仿真數據Fig.3 Simulation data of target tracking initiation without initiation delay

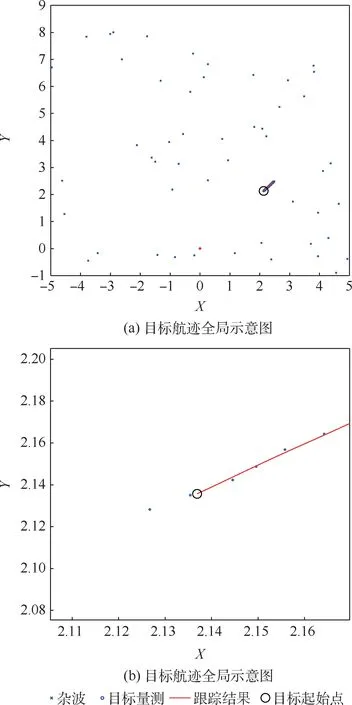
圖4 延遲起始的目標跟蹤起始仿真數據Fig.4 Simulation data of target tracking initiation with initiation delay

通過設置不同的雜波環境(λ值)和目標航跡起始條件(d值),圖5 和圖6 統計了100 次蒙特卡羅仿真實驗的目標跟蹤結果的平均值,考察了不同參數設置條件下目標跟蹤的穩定性與航跡起始的及時性。

圖5 給出了目標航跡起始位置與參考點不同距離情況下(d=0.1, 0.5, 1.5, 2.5, 3)目標航跡起始延遲周期隨雜波環境的變化情況。 可見,隨著雜波數量的增加(λ=0 ～1.5),目標航跡起始的延遲周期波動性增加,較多的雜波影響了目標關聯的及時性,導致了航跡起始的延遲。 延遲周期曲線的波動性可能與蒙特卡羅實驗的次數有關,其波動性會隨著實驗次數的增加而降低。由圖5 的實驗結果可知,當d<3(d=0.1, 0.5,1.5, 2.5)時,航跡起始延遲周期曲線的取值范圍變化不大,總體上小于1,明顯優于3 個掃描周期完成航跡起始的邏輯法[9]。 即使當d= 3時,航跡起始延遲周期曲線的取值仍然總體小于3。

圖6 給出了不同雜波環境下(λ=0.1, 0.5,1.0, 1.5, 2.0)目標航跡起始的延遲周期隨航跡起始點與參考點距離的變化情況。 與圖5 所得結論類似,隨著相對距離的增加(d=0 ～2.5),每條航跡起始延遲周期曲線具有一定起伏,但總體取值范圍的變化不大。 另外,當雜波較少時(λ=0.1),航跡起始延遲周期接近于零,幾乎沒有延遲;當λ取值逐漸增大時,航跡起始延遲周期隨之增大,但總體不大于3。

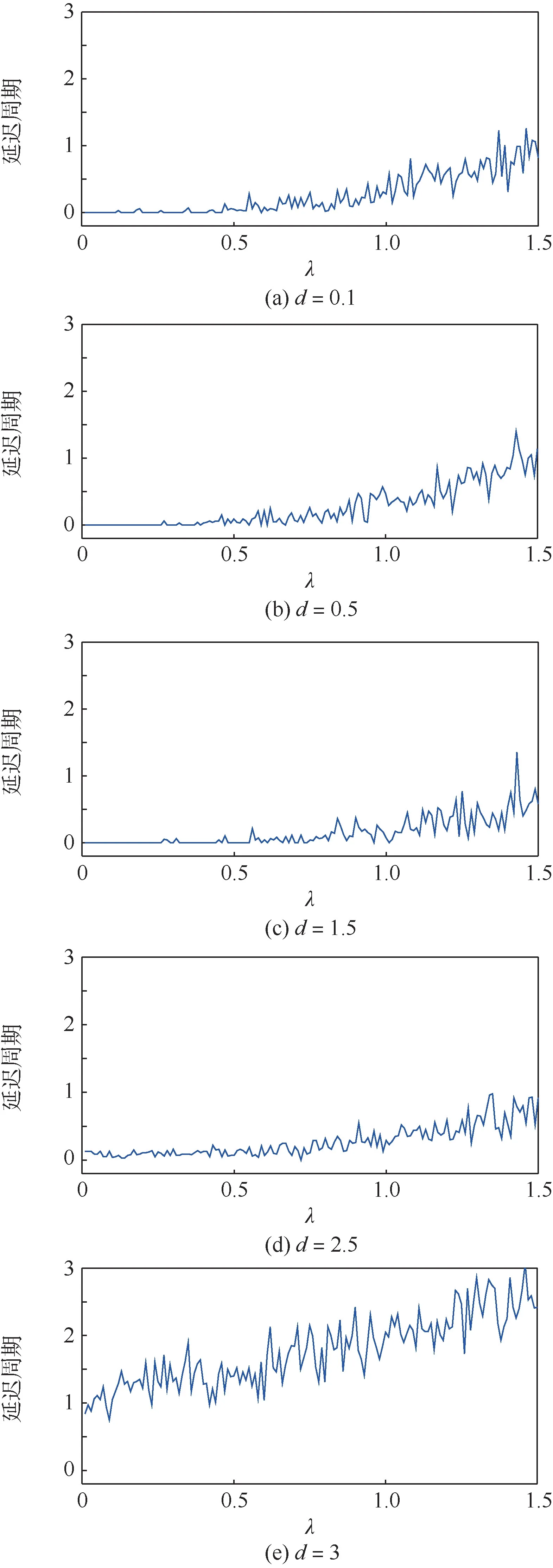
圖5 不同雜波條件下的目標跟蹤延遲周期Fig.5 Target tracking delay period under different clutter conditions

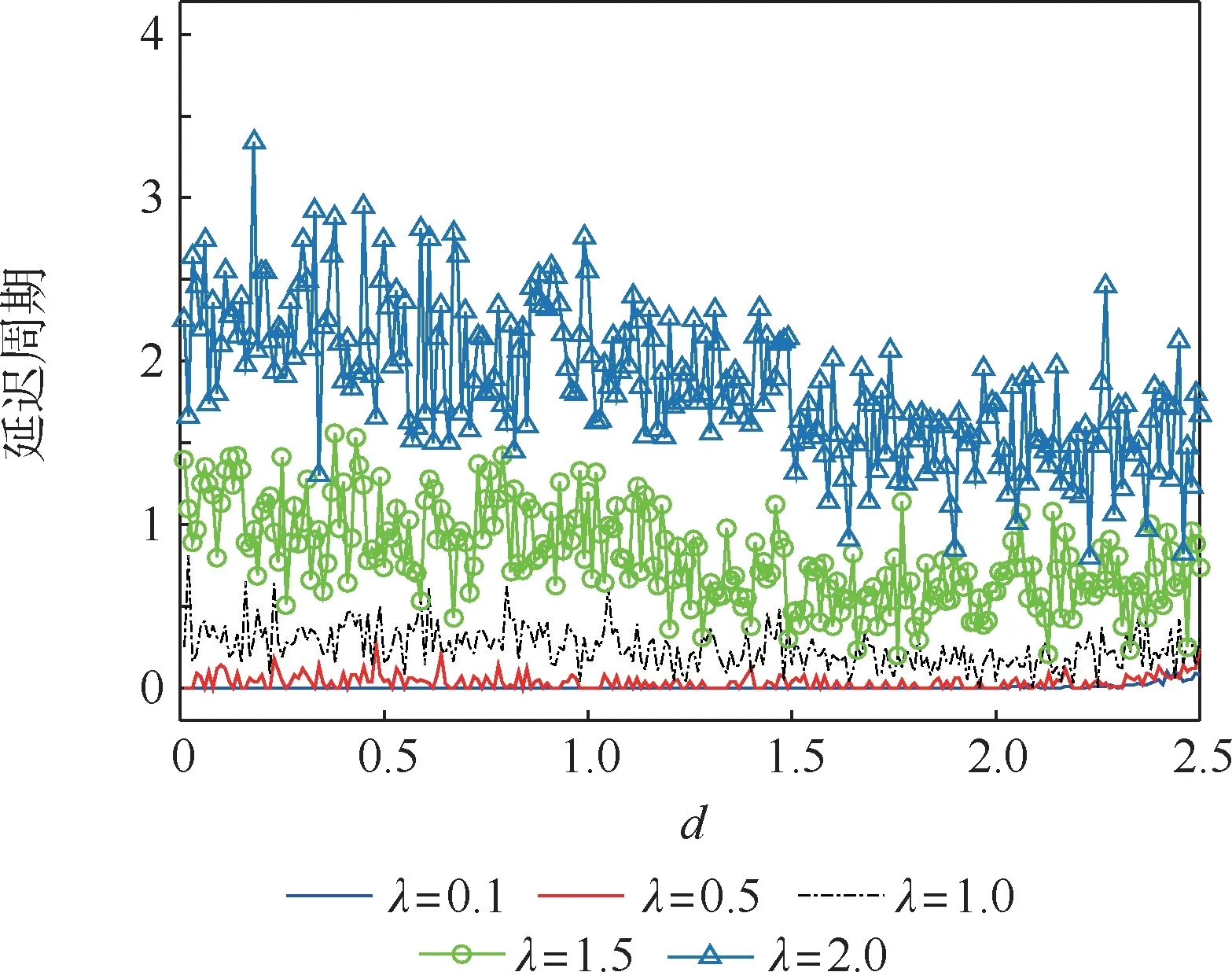
圖6 不同起始條件下的目標跟蹤延遲周期Fig.6 Target tracking delay period under different initiation conditions

表1 給出了λ不同取值情況下航跡起始延遲周期曲線的平均值,全部小于2,低于3 個掃描周期完成航跡起始的邏輯法。 當λ=2.0 時,本文算法所得的航跡起始延遲周期平均值為1.858 3,這是由仿真數據中混入的雜波造成的,本文建立的仿真模型中用一部分雜波數據替換了目標量測數據,導致了目標航跡一定程度的延遲起始。

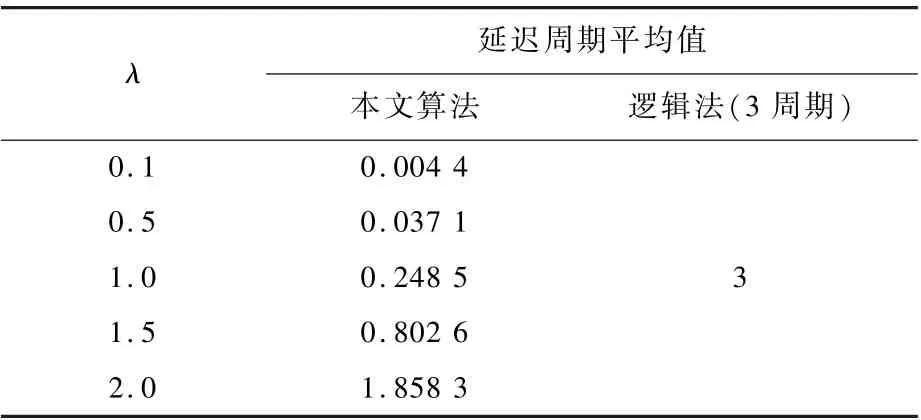
表1 目標航跡起始延遲周期平均值對比Table 1 Comparison of delay periods of target path initiation

3.2 多目標生命周期仿真分析

如圖7 所示,本實驗設計的仿真總步數為500,時間步長為0.01,對依次起始的3 個目標航跡進行了仿真。 目標1 的生命周期為t=0 ～5,其從( -0.25, -1.5)出發,在t=0 ～2 以速度(0,1)勻速運動,在t=2 ～4 完成左轉彎,在t=4 ～5以速度( -1,0)勻速運動,直至航跡結束;目標2的生命周期為t=1 ～4.5,其從(0, -1.5)出發,在整個生命周期中以速度(0,1)勻速運動,直至航跡結束;目標3 的生命周期為t=0.5 ～4.5,其從(0.25, -1.5)出發,在t=0.5 ～3 以速度(0,1)勻速運動,在t=3 ～4 完成右轉彎,在t=4 ～4.5以速度(1,0)勻速運動,直至航跡結束。 目標的真實運動軌跡如圖7 中實線所示,“ ?！贝砟繕肆繙y,其附加了一定的高斯噪聲,“ ×”代表雜波,其參數設置為λ=0.1,均勻地分布在[ -3,2] ×[ -2,3]的區域內。 在數據關聯中,粒子數設定為N=50,pb設定為0.01,cp設定為0.02,cd設定為1/16,目標航跡的起始參考點設置為(0,0)。

圖7 和圖8 對比了在目標消亡模型設置不同參數的情況下3 個目標航跡的跟蹤結果和目標數目估計結果,2 組實驗都實現了雜波環境中全部目標航跡的及時起始和穩定跟蹤。 在航跡終結時間估計方面,當目標消亡模型中的參數設置為α=2 和β=0.5 時,其對目標航跡起始與消亡時間的判斷與真實情況基本相符,如圖7(a)和圖8(a)所示。 當目標消亡模型中的參數設置為α=2 和β=2.5 時,其對目標消亡時間的判斷出現延遲,目標2 和目標3 的航跡在t=4.5 均未能及時結束,導致目標數據的估計結果出現偏差,如圖7(b)和圖8(b)所示。 可見,參數β通過改變目標航跡與量測關聯的中斷時間控制目標消亡概率,β值越大,目標消亡概率越低。

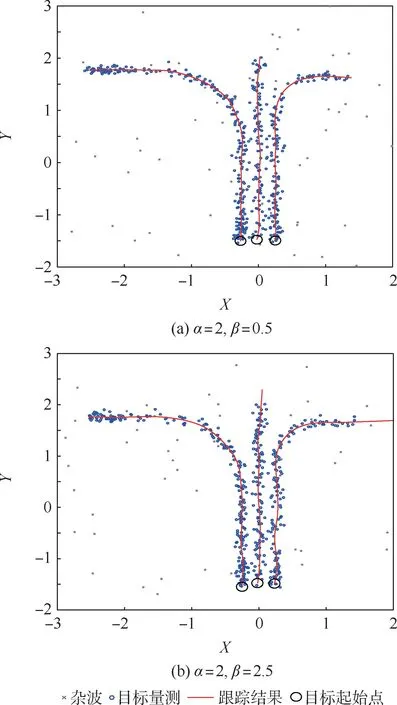
圖7 多目標跟蹤仿真實驗Fig.7 Multi-target tracking simulation experiment

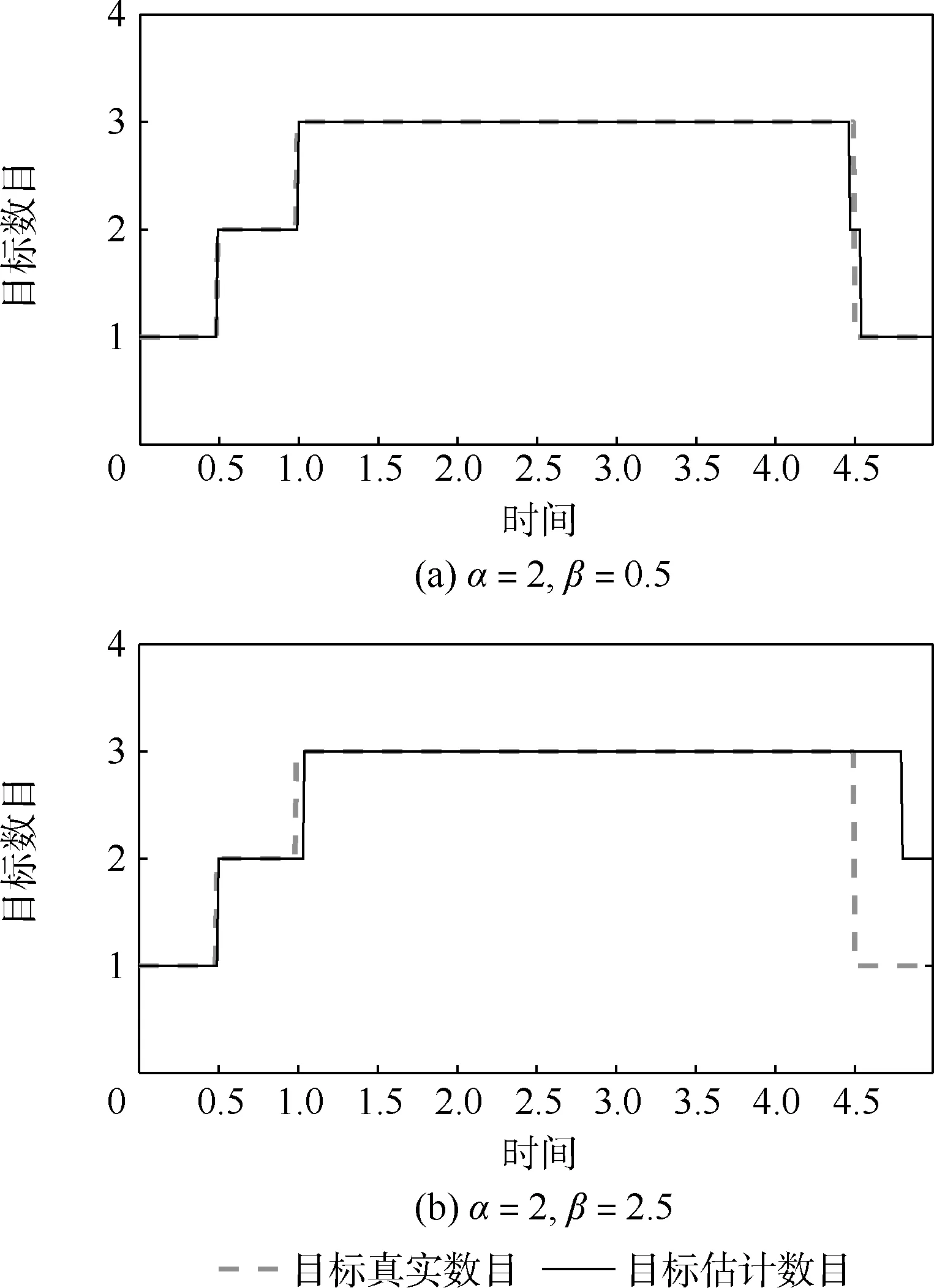
圖8 目標數目估計Fig.8 Target number estimation

4 探鳥雷達實測數據處理

本節基于探鳥雷達在國內某機場獲取的鳥情數據,采用多目標航跡自動起始跟蹤算法,對機場周邊的鳥類目標數量進行統計分析。

4.1 系統平臺

圖9 為中國民航科學技術研究院探鳥雷達實驗系統。 該系統對S 波段導航雷達進行了升級改造,采用可靠性更高且發射功率較小的固態發射機替代原有的磁控管,引入脈沖壓縮和脈沖多普勒等多項信號處理技術,開發了專門的鳥情數據處理與統計分析軟件,改善了其在復雜低空環境中對飛鳥目標的探測能力,該系統放置于某機場燈光站附近,已獲取并積累了大量機場周邊鳥情信息。

圖9 中國民航科學技術研究院探鳥雷達實驗系統Fig.9 CAST experimental avian radar system

4.2 鳥情數據處理分析

機場周邊的鳥類活動通常遵循一定規律,利用探鳥雷達獲取的機場及周邊區域鳥情信息,對機場留鳥的活動節律進行統計分析,能夠掌握機場周邊的鳥類數量與分布情況。 本節基于中國民航科學技術研究院探鳥雷達實驗系統獲取的國內某機場飛鳥目標數據,給出了機場周邊鳥類目標數量進行統計分析的基本步驟及實例。

1) 鳥類活動時段統計

基于探鳥雷達獲取的該機場某日的鳥情信息,統計探鳥雷達監視范圍內全天中每小時出現的飛鳥目標量測數量,經統計,第8 個時段(7:00—8:00)和第18 個時段(17:00—18:00)出現了2 次鳥類活動高峰。 結合機場周邊的鳥情人工調研結果,該機場周邊的鳥類通常會在機場周邊筑巢,并在特定時間進入飛行區覓食。 以上雷達觀測結果與人工調研結果吻合,這2 個時間段可以判定為周邊鳥類的離巢和歸巢時間。

2) 鳥類活動網格分布統計

在探鳥雷達的監控范圍內劃分網格,該區域面積為L×L,單位為m2。 每個網格的面積為l×l,單位為m2。 本例中,探鳥雷達的覆蓋半徑為3 km,L=6 000 m,l=100 m,監控范圍內網格總數為60 ×60,如圖10 所示,左上角設置為坐標系原點(0,0),X軸水平向右,Y軸垂直向下。 在機場周邊的鳥類離巢時間段(7:00—8:00)內,鳥類目標量測超過一定閾值的網格均做顏色標記。 對于標記后的網格分布圖進行腐蝕和膨脹等二值圖像處理,消除其中的孤立點,形成圖10 所示的連通區域即熱點,結合機場周邊的鳥情調研結果,可判定為鳥類的棲息地。 以該熱點區域的中心點作為目標起始的參考點,本例中,該參考點坐標為(4 750,2 650) m。

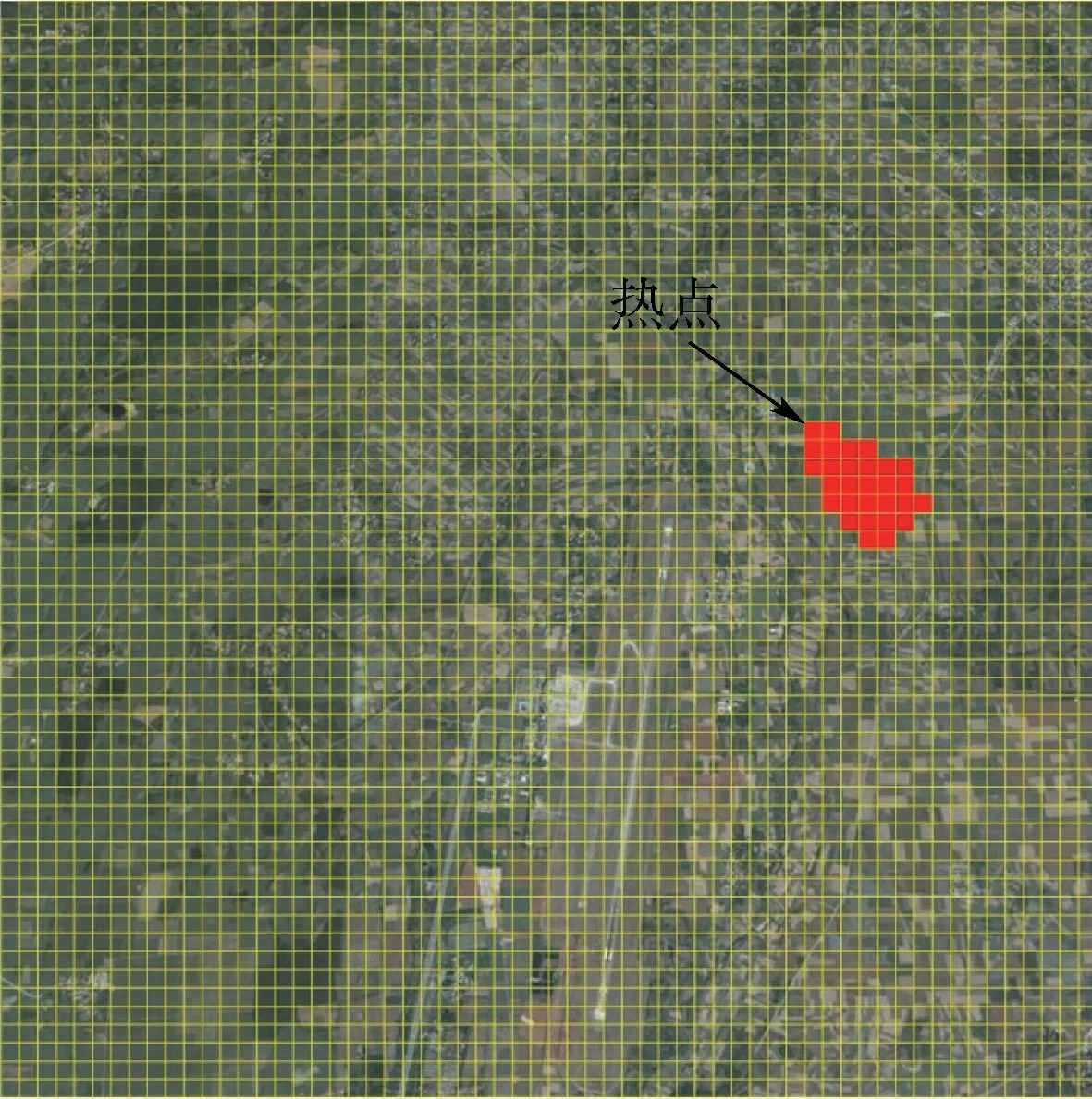
圖10 機場周邊鳥類活動熱點統計結果Fig.10 Hot spot statistics of bird activities around airport

3) 鳥類數量統計分析

圖11 為某日清晨鳥類飛離熱點區域內棲息地的飛行軌跡分布情況,包括雷達覆蓋范圍內的全局圖和鳥類飛行軌跡的局部放大圖。 該鳥類棲息地位于飛行區外東北方向,圖11 的離巢過程發生在7:00—8:00 之間,持續約1 min,種群數量在20 只左右,飛行方向大體為西南,通常會進入飛行區取食。

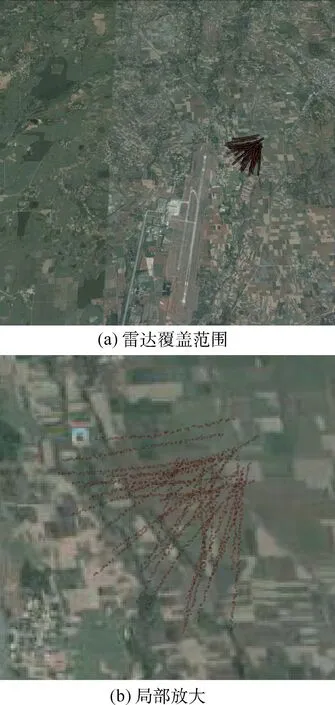
圖11 鳥類飛行軌跡分布Fig.11 Flight path distribution of birds

圖12 為不同日期清晨7:00—8:00 對該棲息地內離巢鳥類目標數量進行估計的結果,目標跟蹤時間持續約70 s。 在數據關聯中,粒子數設定為N=50,pb設定為0.01,cp設定為0.02,cd設定為1/16,目標航跡的起始參考點設置為(4 750,2 650)m。 目標消亡模型中的參數設置為α= 2和β=0.5。 以每次鳥類目標數目估計過程中的最大值作為該種群數量的估計值,因此,第1 次估計結果為23 只,第2 次估計結果為22 只。 表2給出了該棲息地連續10 天的鳥類目標數量統計結果。 可見,該鳥類的種群數量約20 ～30 只,且與人工觀測結果基本吻合。

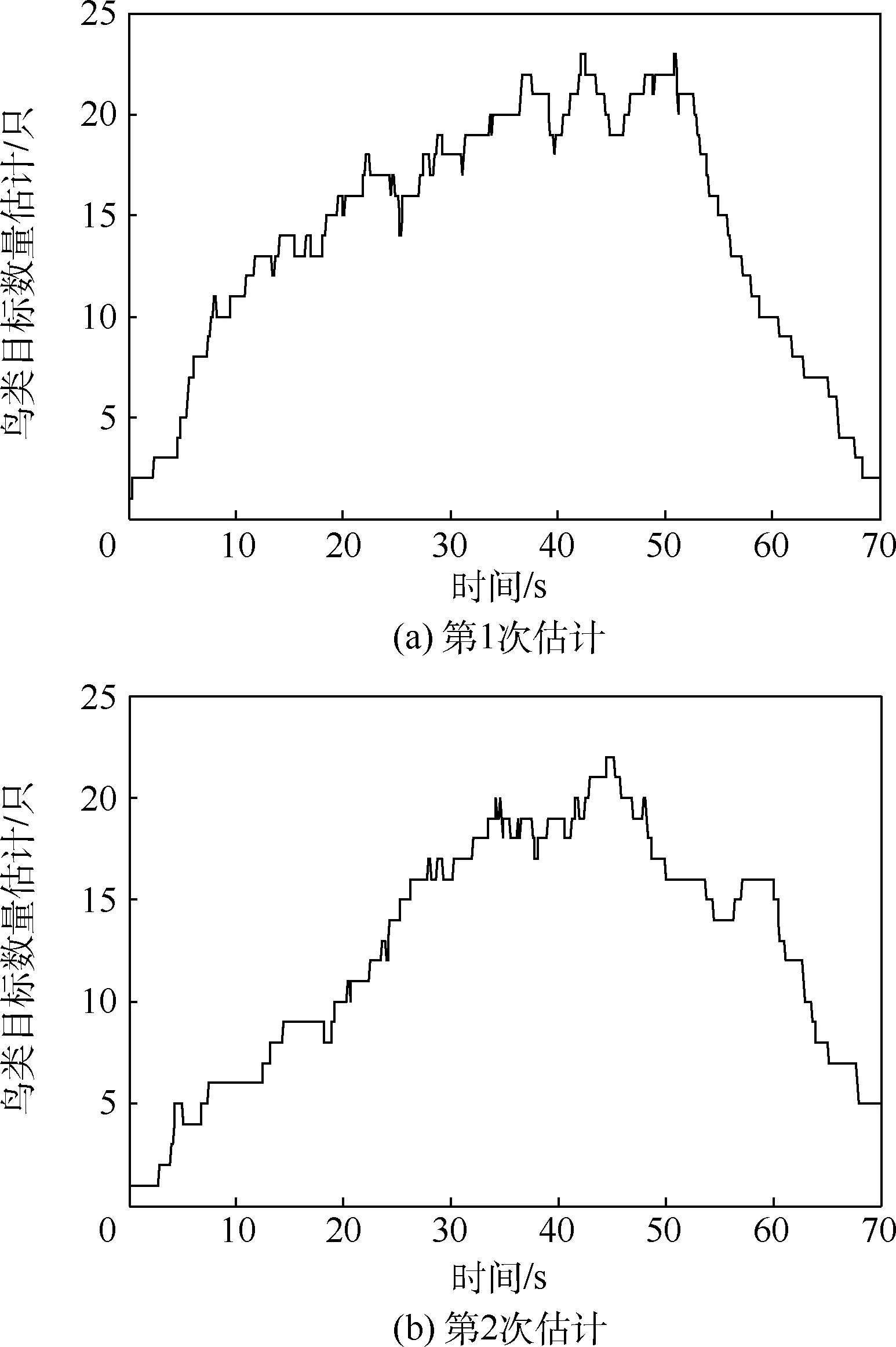
圖12 鳥類數量估計Fig.12 Bird number estimation

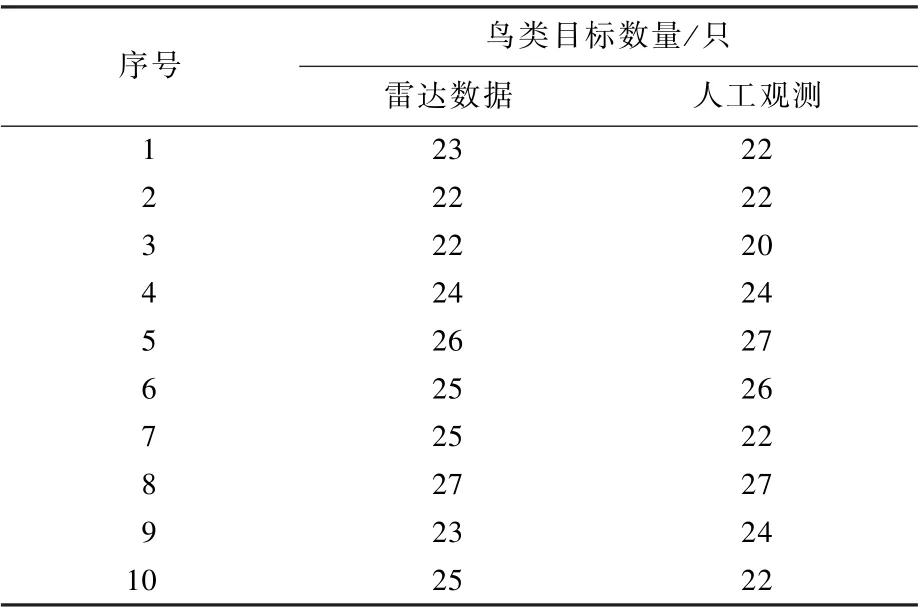
表2 鳥類目標數量估計結果Table 2 Estimation results of bird target number

5 結 論

本文基于粒子濾波數據關聯算法,通過建立目標的新生與消亡模型,較好地實現了雜波環境中雷達多目標的自動起始跟蹤,并將其成功應用于機場周邊的鳥類目標數量估計問題,得出以下結論:

1) 本文提出的自動起始跟蹤算法在數據關聯之前設定了一個公共的新生目標起始關聯點,通過計算量測值與該起始點的關聯概率,判斷其是否屬于新生目標。 該起始關聯點的選擇基于對目標運動軌跡起始范圍的掌握,在一定程度上依賴先驗知識。

2) 通過仿真實驗證明,本文算法在目標起始的及時性方面明顯優于3 個或4 個掃描周期起始的邏輯法,即使在雜波環境中,其目標起始的延遲周期仍然小于2。

3) 本文算法的局限性在于其適用于目標起始區域范圍相對集中的多目標自動起始跟蹤問題,對于目標起始點分散的情況,工程應用中仍推薦3 個或4 個掃描周期起始的邏輯法。

4) 將本文算法應用于機場周邊的鳥類數量統計分析,能夠掌握機場周邊鳥類的棲息地分布、種群數量及活動規律,進而指導機場開展有針對性的生態環境治理措施,有效提升機場鳥擊防范科學水平。