非規則軸承故障的動力學建模與仿真

王震 楊正偉 何浩浩 明安波 張煒

(1. 火箭軍工程大學 導彈工程學院, 西安 710025; 2. 西安交通大學 機械工程學院, 西安 710049)

航空發動機體現了一個國家的科技水平、工業實力和綜合國力,與國民經濟發展和國家軍事安全息息相關。 現代航空發動機大多采用雙轉子甚至三轉子結構,高、低壓轉子通過多個主軸軸承支承于發動機機匣上,為提高推重比,通常將高壓轉子的后支點設計成軸間軸承形式,或稱中介軸承,即高壓轉子前端通過前軸承支承在與機匣連接的固定支承結構上,而后端通過中介軸承支承在低壓渦輪軸上[1]。 中介軸承作為一種特殊的主軸軸承,是實現運動傳遞和承受載荷的關鍵部件,此外航空發動機轉子-軸承系統的運行條件與常規旋轉機械相比,系統結構更加復雜,高溫、高速、重載的工作環境使得主軸軸承更易發生打滑現象并導致點蝕、剝落等故障,對轉子系統甚至發動機的運行性能產生重大影響[2-3]。 因此,深入探討航空發動機主軸軸承的故障機理,建立有效的、符合工程實際的滾動軸承故障動力學模型,對及時發現軸承的早期故障,預防重大事故的發生具有十分重要的意義。

作為一種特殊的滾動軸承,主軸軸承的研究大多可以借鑒普通的滾動軸承研究成果。 但是,現有的軸承故障研究大多是將故障簡化為矩形凹槽或圓形凹坑等規則形狀,與現實的故障形貌存在較大差別。 Kankar 等[4]基于位移激勵的方法,通過改變滾動體與滾道之間間隙量的方式,將內外圈及滾動體上的局部故障表征為滾道或滾動體表面的矩形凹槽。 東亞斌等[5]建立了單一局部故障的滾動軸承模型,將故障定義為截面為矩形的凹坑,同時還分析了故障的寬度、深度和是否處于載荷區等因素的影響,但該模型中假設保持架處于靜止不動狀態,與滾動軸承實際運轉情況顯然不符。 Sawalhi 和Randall[6-7]在表征故障引起的間隔量變化時,采用一個故障深度隨轉角呈錐形變化的函數來模擬,更加真實地描述了滾動體進出故障的軌跡,實現了軸承故障的精細建模,進一步改進了基于位移激勵的軸承故障模擬方法。陳果[8]針對航空發動機轉子系統中的軸承故障建模問題,用半圓形凹槽來引入軸承局部故障,改進了局部故障的形貌。

在工程實際中,軸承的故障形貌往往呈現出顯著的不規則特征,與矩形或半圓形等規則形狀差別很大。 鑒于此,本文提出了滾動軸承非規則局部故障的表征方法,并通過單轉子系統進行驗證,對掌握含故障軸承轉子系統的動力學特性、提高轉子系統的運行可靠性具有重要的理論意義和實用價值。

1 單轉子-軸承系統模型

軸承故障動力學分析是深入了解軸承故障特征的重要途徑之一。 但是在實際應用中,主軸軸承作為航空發動機的關鍵支承部件,航空發動機極端惡劣的工作環境和運行特點使得轉子和軸承之間的相互作用更加突出[9]。 傳感器采集到的振動信號是包含了整個轉子系統的振動響應,相比于單純軸承故障動力學建模而言,整個系統涉及的運行環境和邊界條件更為復雜,將軸承從轉子系統中孤立出來進行動力學特性研究與實際工況明顯不符[10]。 因此,在軸承故障動力學建模中,考慮轉子系統的影響,更加深入地分析軸承-轉子系統的動力學特性對于發動機實際工況的研究及后續軸承故障診斷工程應用具有重要意義。

1.1 軸承-轉子系統模型

以單盤對稱轉子模型作為分析對象,建立含不平衡故障的轉子-滾動軸承動力學模型,如圖1 所示。 實際發動機的轉子系統要比這一模型復雜得多,但根據此模型可以說明實際轉子的振動現象。

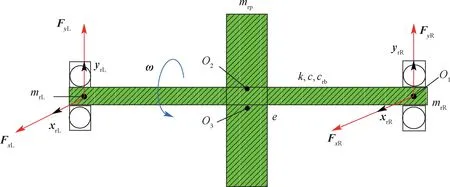
圖1 單轉子-軸承系統Fig.1 Single rotor-bearing system

在模型中,O1、O2、O3分別為軸承幾何中心、轉子幾何中心、轉子質心,mrL、mrR分別為轉軸左、右兩端在軸承位置的轉子集中質量,mrp為轉子在圓盤處的集中等效質量,e為轉子質量偏心,k為彈性軸的剛度,c和crb分別為轉子在圓盤處和軸承處的阻尼系數,ω為轉子的轉速,FxR、FyR為右端軸承的支承反力,FxL、FyL為左端軸承的支承反力。 由牛頓第二定律可得系統的運動微分方程為

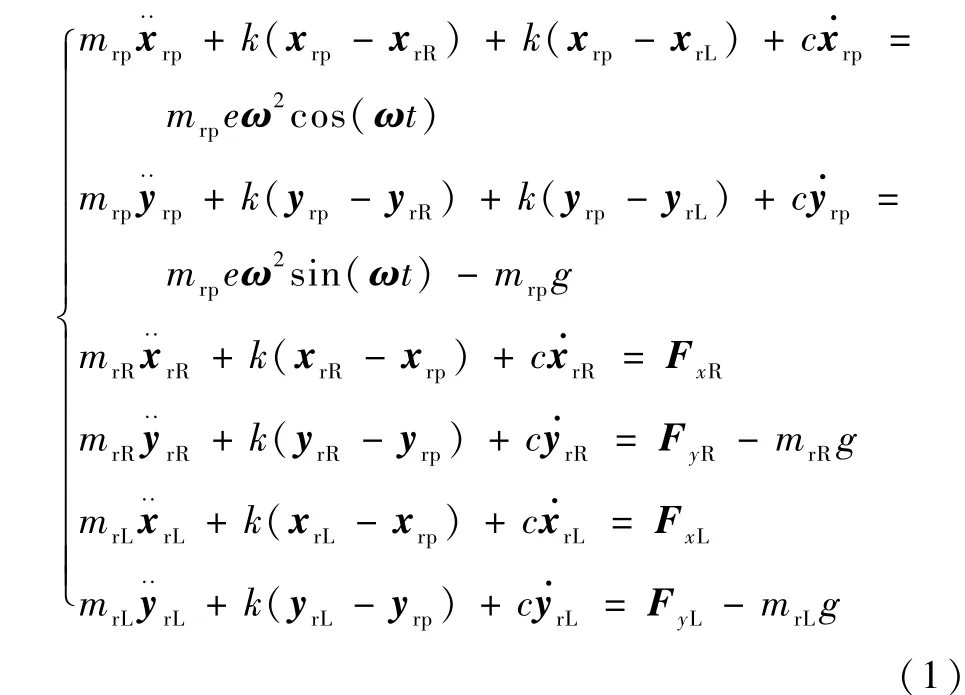
式中:g為重力加速度。

1.2 軸承力模型

假設軸承內圈固定在旋轉軸上隨轉軸一起旋轉,外圈固定在軸承座上保持不動,如圖2 所示。滾動體在運轉時每通過一次載荷區就會產生一次振動,即VC 振動[11]。 同時,滾動軸承也因為轉子系統的不平衡激勵而產生強迫振動。

圖2 軸承力模型Fig.2 Bearing force model

設第j個滾珠的位置為θj,有

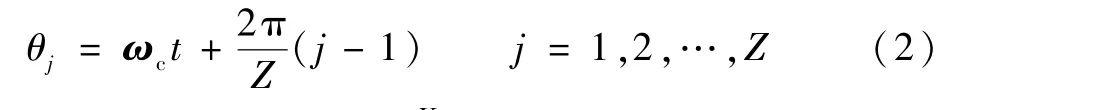
式中:ωc為保持架的旋轉速度;Z為滾珠數目。

設內圈滾道半徑為r,外圈滾道半徑為R,有

設內圈中心在橫軸和縱軸產生的位移分別為x和y,軸承的初始間隙為δ0,軸承由于故障產生的間隙為λD,則第j個滾珠與滾道間的法向接觸變形量為

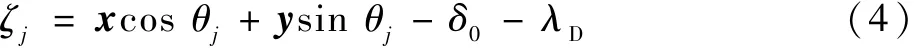
根據非線性赫茲彈性接觸理論,可得滾動接觸的第j個滾珠與滾道所產生的接觸壓力Fj,又因為滾珠與滾道間產生壓力的條件為接觸變形,即ζj> 0 時才有作用力,可以利用η來表征。 則

1.3 軸承非規則故障模型

采用隨機數據數列模擬故障表面形貌,滾動體通過故障區域時,通過改變接觸區域間隙的形式來引入位移激勵[12]。 故障表面可看做是由一系列高度隨機變化的點構成,高度的分布可以反映出表面的重要信息,建立故障粗糙表面模型的步驟如下:

步驟1 生成一個均值為0、方差為1 的隨機高斯噪聲序列。

步驟2 鑒于高斯噪聲序列數據點的幅值變化太劇烈,與實際的軸承故障形貌不相符。為了使滾動體在通過故障表面時緊貼故障表面滾動,對隨機噪聲進行低通濾波。 濾波器的波長需要根據滾動體的半徑進行設定,具體過程如下:

滾動體曲率kball可以用式(8)估算,d為滾動體直徑。 正弦曲線如圖3 所示,表面曲率ksi可以通過式(9)和式(10)計算。 在x=3λ/4 處滾動體與表面曲率一致,目的是為了使滾動體可以順利在滾道兩頂點之間滾動。

圖3 波長導出Fig.3 Wavelength export

濾波后信號如圖4 黑線所示。 理想模型下,滾動體在經過故障區域時會瞬間釋放全部變形量,離開故障時,又會瞬間重新獲得接觸變形。 然而在實際中,變形量的釋放和獲得是漸變的,粗糙表面的形成,盡可能地減小了滾動體進出故障的瞬時振動影響。

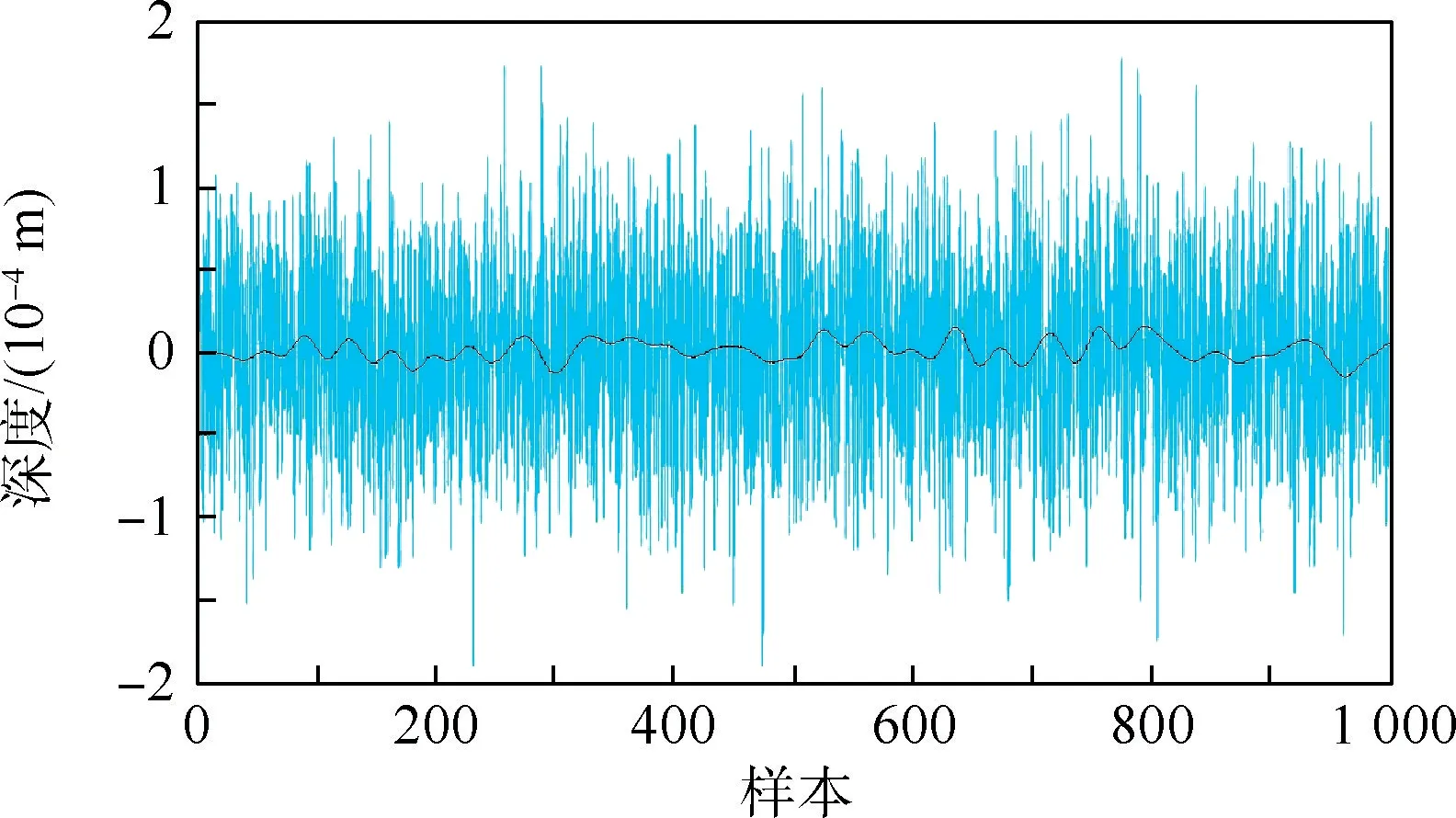
圖4 低通濾波信號Fig.4 Low-pass filtered signal

1.4 滾動軸承外圈故障建模

軸承因為長時間運行和受到滾動體的頻繁沖擊,外圈滾道易產生點蝕、剝落等故障[13],故障形貌常呈現出非規則特征。 圖5 為軸承外圈故障模型。 圖中:LD為損傷表面的寬度。

滾珠在經過故障區域時,軸承間隙會發生變化,滾珠與軸承內外圈的赫茲接觸力會因為軸承間隙的改變而降低或變為零。 故需計算滾珠在損傷區域的間隙變化量λD。 將外圈滾道離散化得到共NL個點。 設損傷在外圈的位置為θout,易得出故障在離散軌道上所對應的位置為Np,從圖5(c)中可以看出,外圈故障對應的中心角為β,由此可求得故障在周向寬度上對應的數據長度Nf,在(Np+1,Np+Nf)區域內用隨機數列表征產生的故障,由損傷引起的軸承間隙變化量為

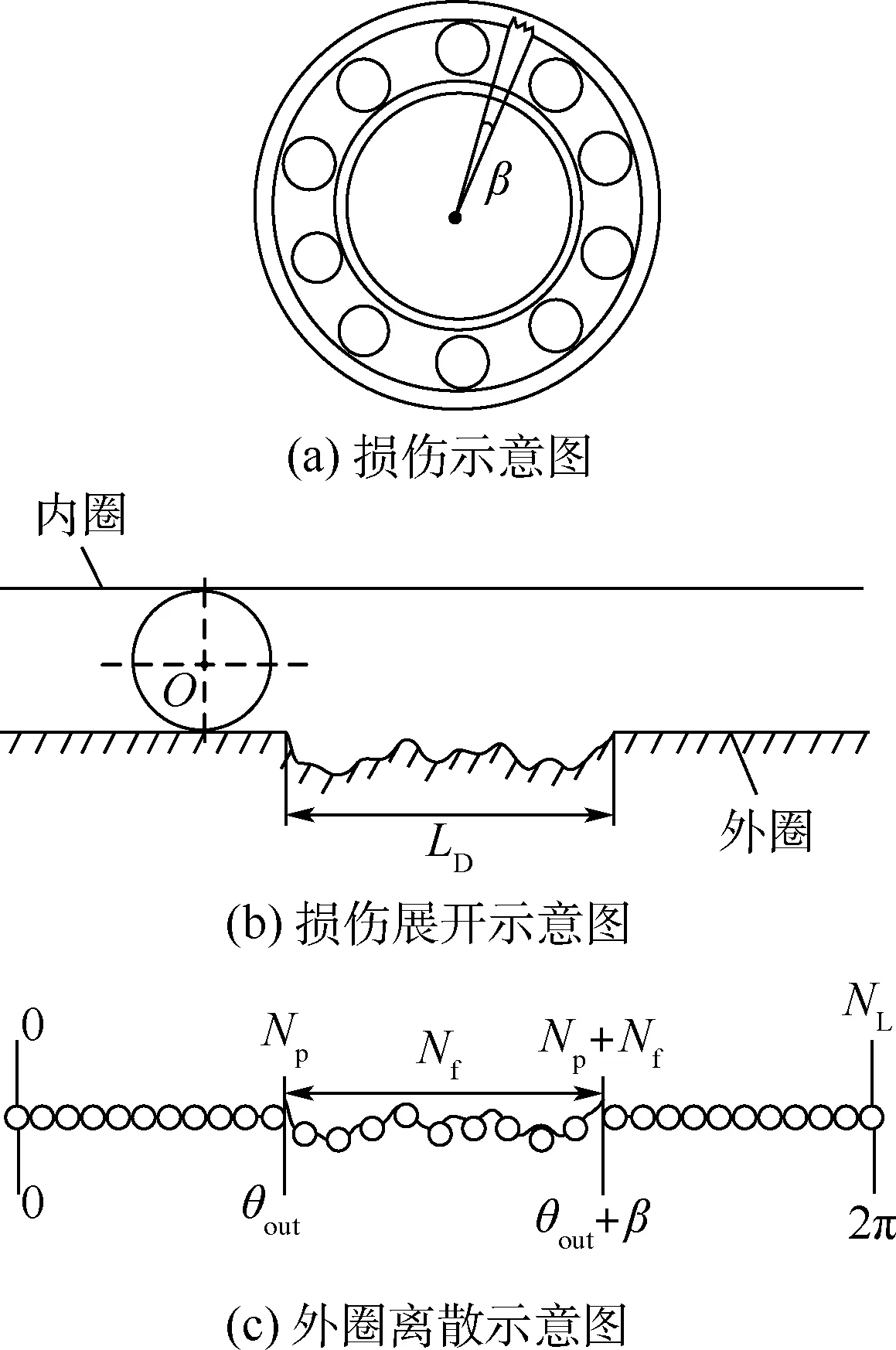
圖5 軸承外圈故障模型Fig.5 Bearing outer ring failure model

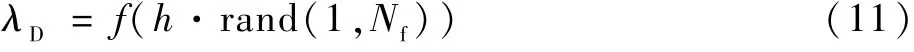
式中:h為深度;f為低通濾波函數。

需要說明的是,式(12)相當于用一個質點來表示滾動體,與真實的滾動體進出故障區域的過程之間還是存在一定的差別。 進行動力學計算時,只需將λD代入式(4)中。

1.5 滾動軸承內圈故障建模

假設內圈隨轉軸一起轉動,軸承內圈故障建模與外圈過程相同,但軸承內圈滾道產生損傷時,損傷區域的位置隨著內圈的轉動而變化。 因此,滾動體與損傷區域產生沖擊的位置也會隨著損傷區域位置的變化而變化,使得振動時沖擊力大小不同,振幅也會因此而產生周期性變化[14]。 圖6為軸承內圈故障模型。

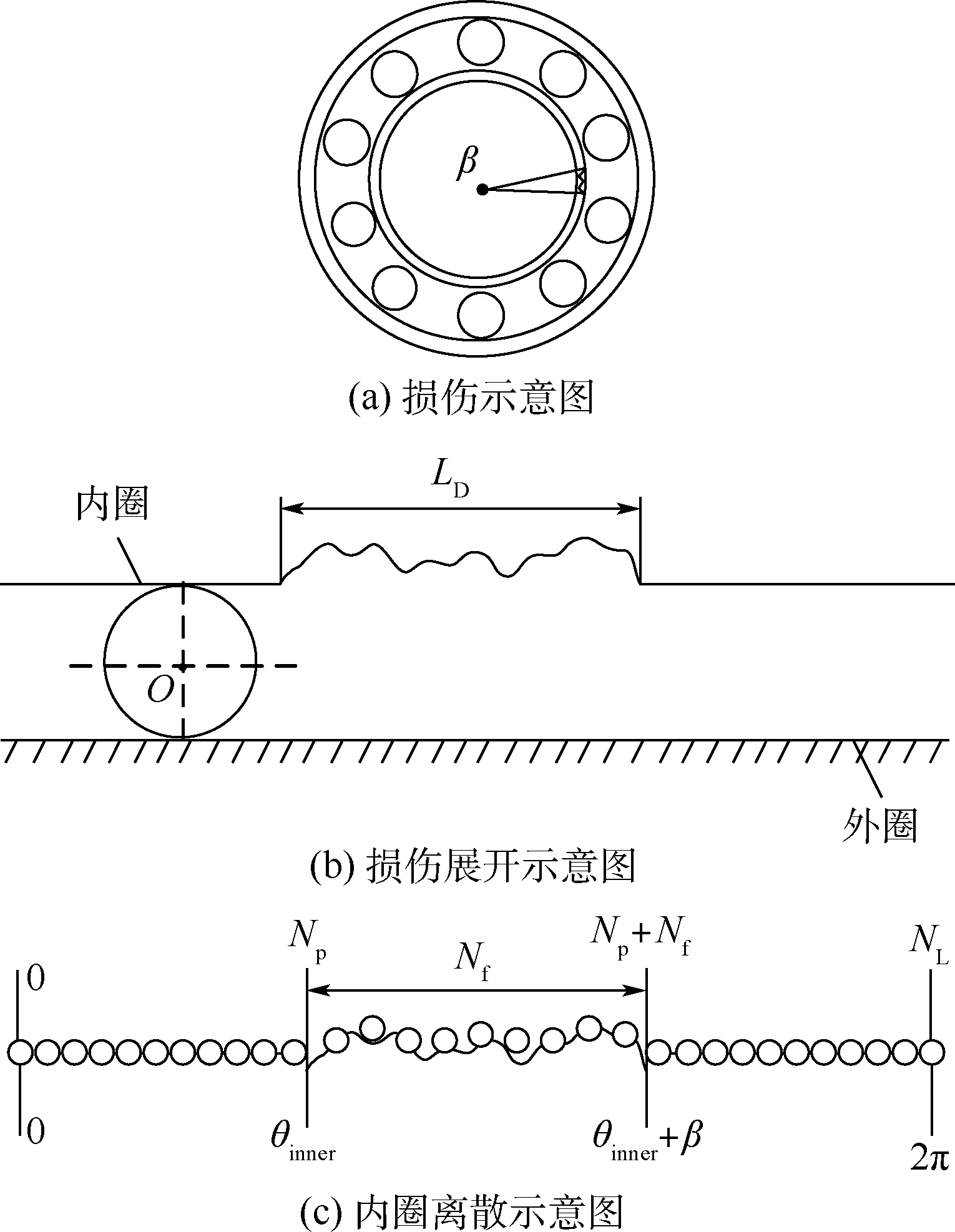
圖6 軸承內圈故障模型Fig.6 Bearing inner ring failure model

2 滾動軸承故障仿真分析

選取的轉子系統的初始參數如下:mrp=32.1 kg,mrL=mrR=4.0 kg,c=2 100 N·s/m,crb=1 050 N·s/m,e=0.05 mm,k=2.5 ×107N/m。 滾動軸承采用2204K 和NJ204E 型滾動軸承,具體參數如表1 所示。

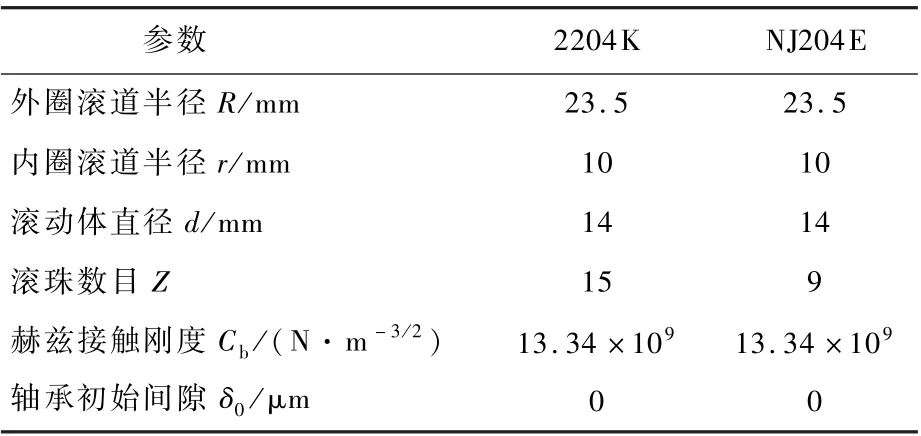
表1 滾動軸承主要計算參數Table 1 Rolling bearing main calculation parameters

當軸承元件的表面出現局部損傷時,軸承系統會被一系列寬帶沖擊所激勵,產生相應的沖擊衰減響應[15]。 這些寬帶沖擊是由特定的通過頻率產生的,頻率大小通常取決于軸承型號和轉速。假設軸承內圈隨著轉軸一起轉動,外圈固定于軸承座。 滾動軸承各故障特征頻率如下。

內圈故障特征頻率為

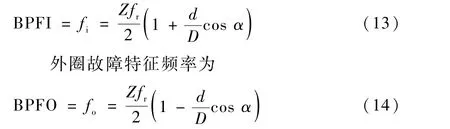
保持架公轉頻率為

式中:fr為轉子的旋轉頻率;D為軸承節徑;α為接觸角,假設α=0°。

2.1 外圈滾道含故障時的振動響應

分析外圈滾道時,采用2204K 型軸承。 設損傷寬度LD=3 mm,損傷深度h=1 mm,損傷位于右端軸承外圈垂直正下方,轉子轉速為600 r/min。由式(14)得,外圈故障特征頻率BPFO≈43.6 Hz,沖擊響應的周期為T=0.023 s。

圖7(a)為轉子右端垂直振動加速度時間波形,可以看出由于損傷所產生的脈沖信號到來時會對軸承產生沖擊作用,此時振動加速度會因受到沖擊而突然增大,損傷的沖擊周期T≈0.023 s,隨著沖擊作用消失,系統產生了一系列衰減振動。從頻域圖(見圖7(b))中可以看出,在共振區域邊頻帶的間隔為43.6 Hz(約為1/0.023),正好是軸承外圈產生故障時外圈的通過頻率BPFO,即外圈故障的特征頻率。 從平方包絡譜(見圖7(c))中可以清楚地看出外圈故障特征頻率及其倍頻。 文獻[16]指出,外圈損傷在頻譜上表現為在共振頻率附近出現一系列譜線,且這些譜線以外圈故障特征頻率為間隔。 仿真結果與文獻結論一致,驗證了軸承外圈故障建模的正確性。

圖7 外圈損傷時轉子右端垂直振動響應Fig.7 Vertical vibration response of right end of rotor when outer ring is damaged

2.2 內圈滾道含故障時的振動響應

分析內圈滾道時,采用NJ204E 型軸承。 設損傷寬度為LD=3 mm,損傷深度h=1 mm。 轉子轉速為600 r/min。 可算出內圈的特征頻率BPFI≈63.8 Hz,周期T=0.015 7 s。

從圖8(a)轉子右端垂直振動加速度時間波形圖中可看出,滾動體在通過內圈故障區域時,會因為間隙的突然改變而產生沖擊作用,使得振動加速度發生突變,沖擊過后,系統又會產生一系列衰減振動。 損傷的沖擊周期T≈0.015 7 s,由于內圈故障隨著轉軸旋轉而不斷改變位置,沖擊的強弱受到了旋轉頻率的調制,振動加速度幅值大小呈現出周期性變化,每隔一個旋轉周期,沖擊作用重復一次。 從頻域圖(見圖8(b))中可以看出,沖擊振動產生的共振峰在1 800 Hz 附近,在共振峰處存在以旋轉頻率為間隔的邊頻帶,而且可以看出波谷間隔為63.8 Hz(約為1/0.015 7),正好等于內圈故障的特征頻率。 圖8(c)中可以清楚地看出軸承內圈故障的特征頻率及其倍頻,在內圈特征頻率左右還存在以旋轉頻率為間隔的邊頻帶,旋轉頻率及其2 倍頻也可以看出。 文獻[16]指出,內圈含有故障時,在頻譜圖上表現為特征故障頻率及其各階倍頻,在各階倍頻兩旁還存在間隔為旋轉頻率的調制譜線。仿真結果與文獻結論一致,從而驗證了滾動軸承內圈故障建模的正確性。

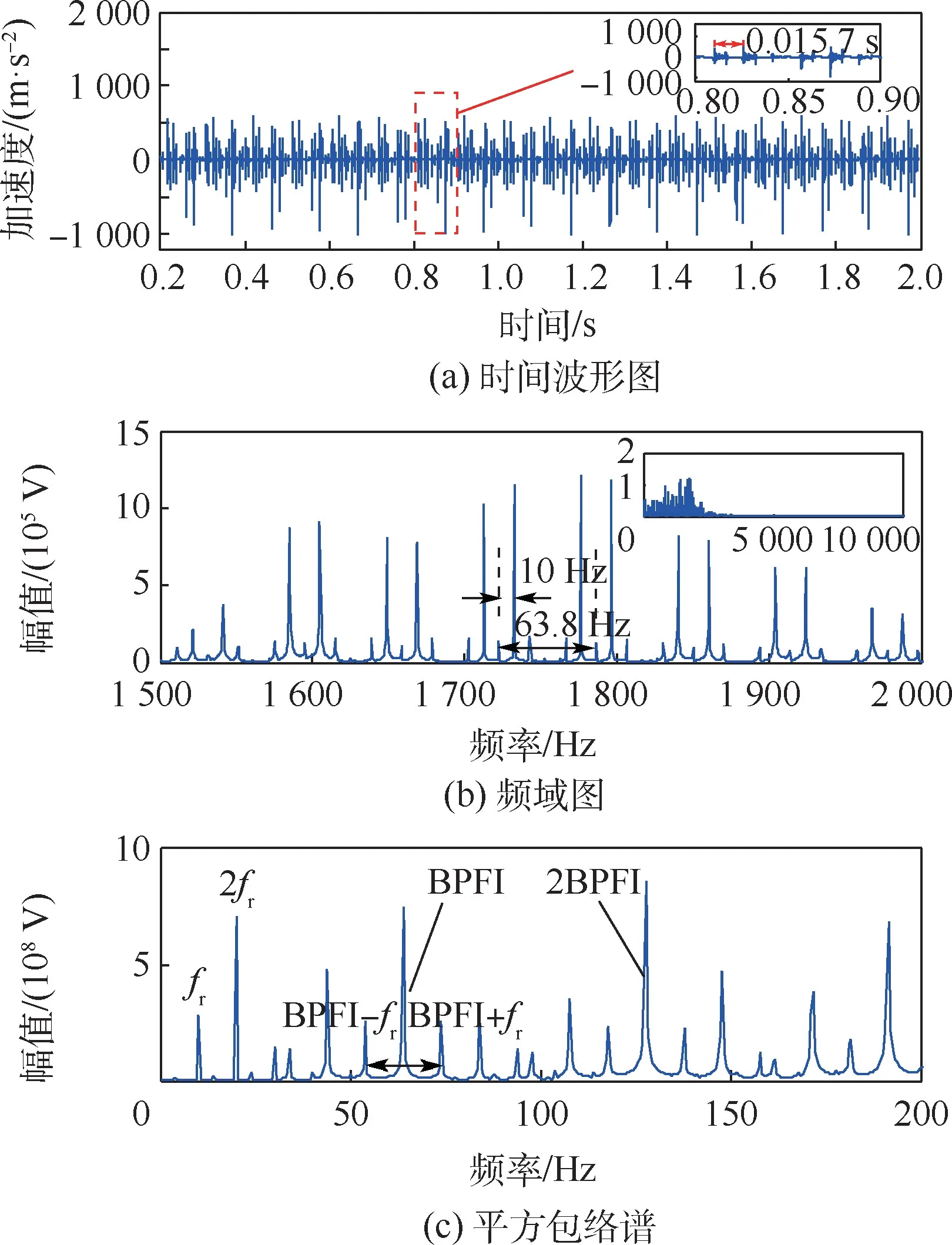
圖8 內圈損傷時轉子右端垂直振動響應Fig.8 Vertical vibration response of right end of rotor when inner ring is damaged

3 軸承故障參數對系統振動響應的影響

為研究軸承故障參數對系統振動的影響,需要先弄清楚滾動體在進出故障時的系統振動變化。 從常見的矩形故障模型出發,在轉子的右端引入相同的軸承外圈故障,通過計算得出轉子右端加速度的波形圖。 從圖9 中可以看出,2 種故障模型在加速度波形圖上最大的區別在于滾動體通過故障區域時波形的變化,矩形故障所表現的是一條直線,而非規則故障是一條非規則曲線?？梢钥闯?矩形故障的雙沖擊現象非常明顯,但與實際情況存在較大差別。

圖9 不同故障形貌的外圈故障及其響應Fig.9 Outer ring faults with different fault topography and their responses

3.1 軸承故障周向寬度的影響

設轉子轉速為600 r/min,故障深度h=1 mm,故障位于右端軸承外圈滾道上,圖10(a)為矩形故障周向寬度LD分別取1 mm、3 mm、5 mm 時,轉子右端加速度變化曲線,圖10(b)為非規則故障時對應的加速度變化。 可以看出,滾動體進出2 種故障的瞬間產生了相同的振動響應,而在經過故障區域時,對于不同的故障形貌,加速度變化有所不同。 不同軸承故障周向寬度所對應的加速度變化范圍存在差別,隨著故障周向寬度的增加,滾動體在進出故障的時間間隔增大,系統的雙沖擊現象會更明顯,而且滾動體離開故障前的加速度變化也在增大,說明沖擊力和沖擊能量隨著故障寬度增大而增加,滾動體對外圈的沖擊越劇烈。

圖10 外圈含不同周向寬度故障時的加速度曲線Fig.10 Acceleration curves when outer ring contains different circumferential width faults

圖11 分別為轉子右端豎直加速度的平均幅值、均方根、峰峰值、峰值的變化曲線。 可以看出,外圈故障時,故障深度相同的情況下,非規則故障產生的沖擊振動要大于矩形故障。 這是因為外圈滾道產生損傷時,損傷區域位置固定,且2 種類型故障深度較小,進出故障區域瞬間沖擊變化差異不大。 主要沖擊差異體現在滾動體在通過故障區域時,經過非規則故障的粗糙表面,波形也是非規則曲線,而經過矩形凹槽故障的光滑底面時,波形所表現的是一條直線,故外圈故障時,非規則故障產生的沖擊振動要大于矩形故障。 此外,對于外圈而言,非規則故障周向寬度大小對系統振動的影響更大,且隨著故障周向寬度的增加而增加,即外圈非規則故障周向寬度是影響系統振動響應的主要故障參數。 從圖11 中還可以看出,當故障周向寬度超過4 mm 時,非規則故障所產生的振動沖擊會顯著增大,這說明了當故障達到一定程度時,系統的振動會急劇增大,引起失效。

圖11 外圈故障周向寬度對豎直加速度的影響Fig.11 Influence of outer ring fault circumferential width on vertical acceleration

假設故障位于右端軸承內圈滾道且故障深度h=1 mm,圖12 為故障周向寬度LD分別為1 mm、3 mm、5 mm 時,不同類型故障所對應的加速度變化曲線。 可以看出,當滾動體進出故障的瞬間產生了沖擊脈沖,由于故障形貌不同,加速度變化曲線產生了較大差異,隨著故障周向寬度的增加,滾動體進出故障的時間間隔也在增大。 此外,圖12中軸承內圈故障周向寬度對滾動體進出故障時的瞬間沖擊幅值的影響需要要用多個不同的沖擊點來看,且沖擊幅值主要是與深度相關的,要在深度上進行分析。 通常,非規則故障的深度采用的是平均深度,表面是粗糙的;矩形故障的深度是確定的,而深度對進出沖擊應該影響是最大的。 對不同故障周向寬度的分析,出發點是為了實現對滾動體通過故障區域的表征,突出滾動體進出故障區域及中間通過時的現象,對系統的振動響應進行觀察分析,通過與理想的矩形故障得出的響應進行對比分析,驗證非規則軸承故障模型的正確性。

圖12 內圈含不同周向寬度故障時的加速度曲線Fig.12 Acceleration curves when inner ring contains different circumferential width faults

從圖13 可以看出,內圈出現故障時,矩形故障計算出來的數值要高于非規則故障計算結果。這是因為內圈故障時損傷區域隨著內圈的轉動而變化。 因此,滾動體與損傷區域產生沖擊的位置也會隨著損傷區域位置的變化而變化,使得振動時沖擊力大小不同,振幅也會因此而產生周期性變化。 非規則故障粗糙表面的形成,盡可能地減小了滾動體進出故障的瞬時振動影響。 而矩形故障進出故障的瞬時雙沖擊現象非常明顯,加上內圈的高速轉動,沖擊更為明顯,故內圈故障時,矩形故障產生的沖擊振動要大于非規則故障。 此外,隨著故障周向寬度增大,不同軸承故障周向寬度所對應的加速度變化差別較小,系統所對應的振幅基本保持不變。 也就是說,對于軸承內圈而言,故障周向寬度影響不大,不是系統振動的主要影響因素。

圖13 內圈故障周向寬度對豎直加速度的影響Fig.13 Influence of inner ring fault circumferential width on vertical acceleration

3.2 軸承故障深度的影響

設轉子轉速為600 r/min,軸承外圈存在故障且故障周向寬度LD=3 mm,圖14(a)為矩形故障的深度h分別為0.1 mm、0.3 mm、0.5 mm時,轉子右端加速度變化曲線,圖14(b)為非規則故障時對應的加速度變化。 可以看出,滾動體在進出故障的瞬間都產生了明顯的加速度變化。 對于不同的故障形貌,加速度的時間波形存在較大差異,隨著故障深度的增加,加速度顯著增大,滾動體對于滾道的沖擊力明顯變大。

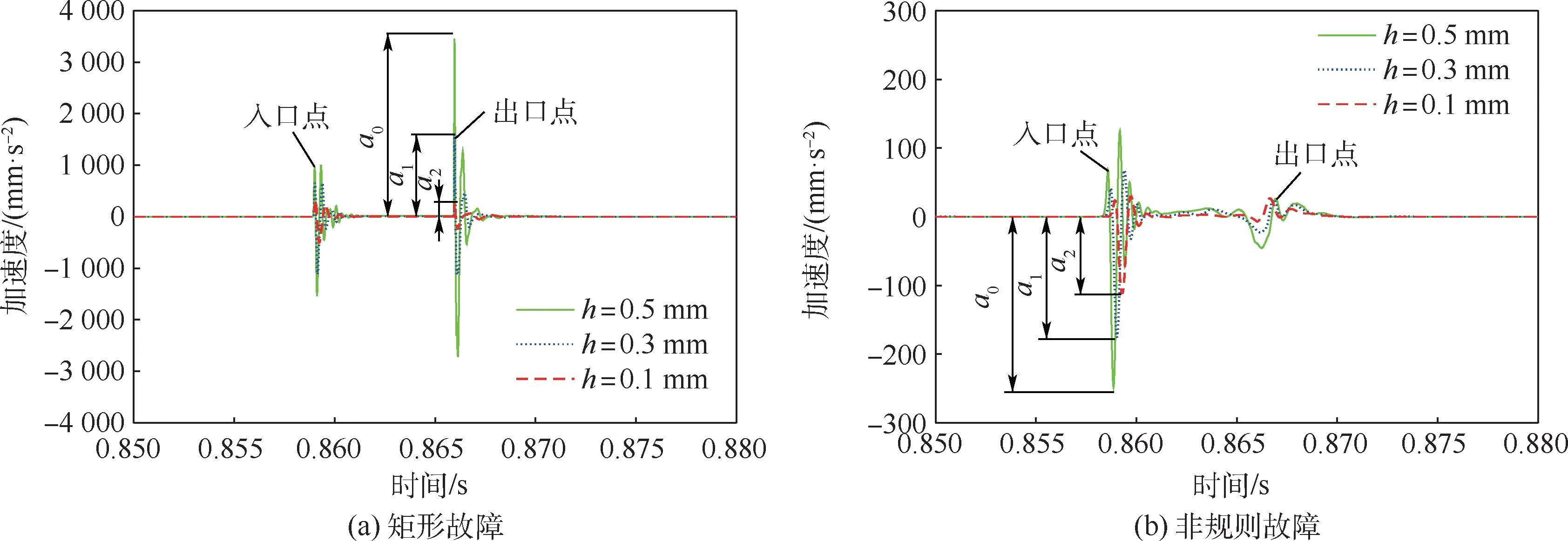
圖14 外圈含不同深度故障時的加速度曲線Fig.14 Acceleration curves for outer ring with different depth faults

從圖15 中可以明顯看出,隨著故障深度增加,矩形故障對應系統振動的幅值變化相比于非規則故障尤為明顯,這是因為在矩形故障模型中,假設滾動體進出故障時是一個瞬時過程,而實際中滾動體進出故障時是一個漸變的過程,因而非規則軸承故障所對應的幅值變化較為平緩。

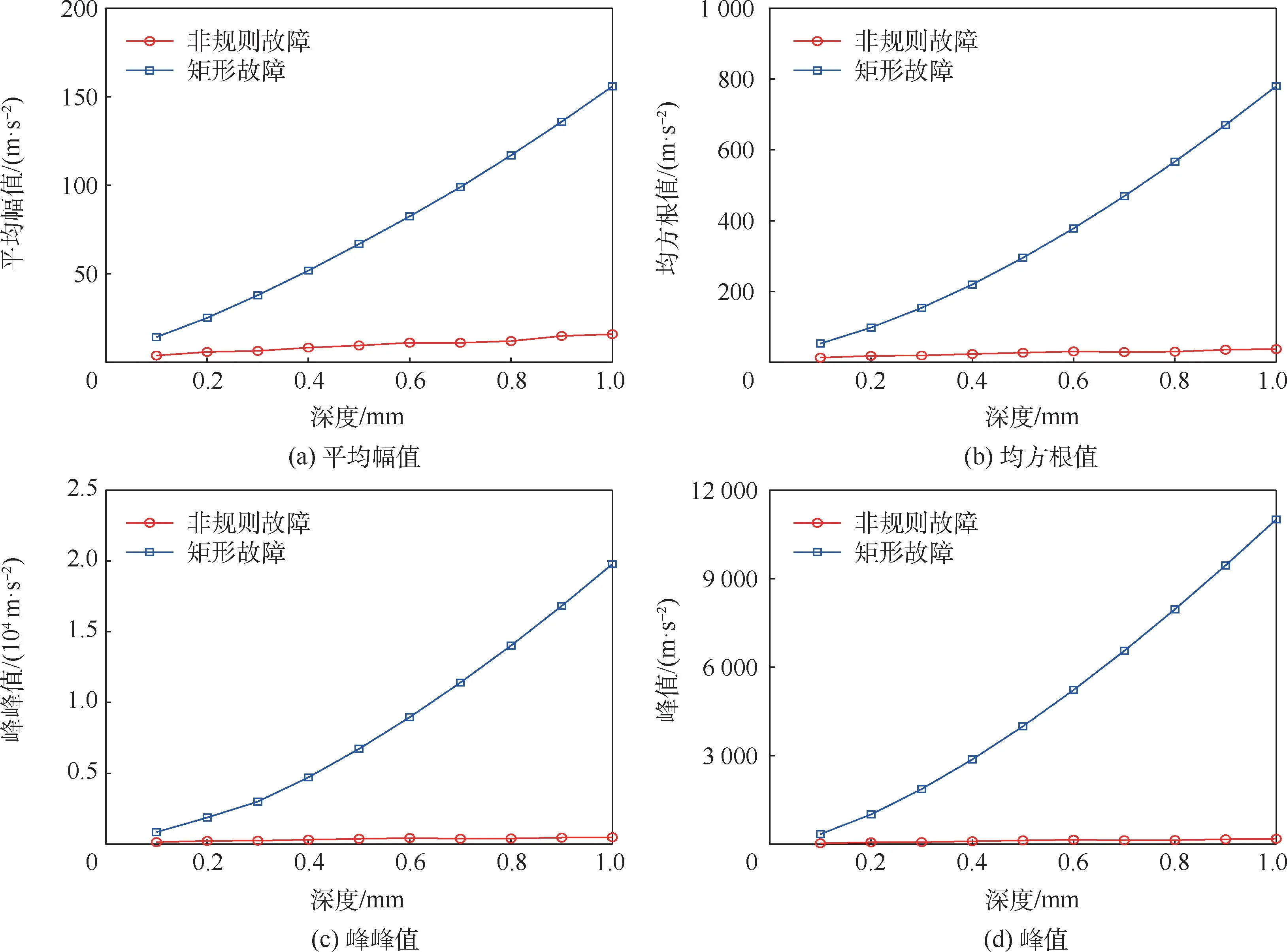
圖15 外圈故障深度對豎直加速度的影響Fig.15 Influence of outer ring fault depth on vertical acceleration

設軸承內圈存在故障且故障周向寬度LD=3 mm,圖16 為故障深度h分別為0. 1 mm、0.3 mm、0.5 mm 時,不同類型故障轉子右端的加速度時域波形圖。 可以看出,隨著故障深度的增加,轉子右端加速度峰值顯著增大,滾動體對于滾道的沖擊力明顯變大。 與外圈故障相比,內圈故障引起的振動沖擊更劇烈。 從圖17 可以看出,隨著故障深度增加,系統振動的幅值也是逐漸增大,相比于矩形故障而言,實際非規則故障引起的加速度振動變化同樣較為平緩。

圖16 內圈含不同深度故障時的加速度曲線Fig.16 Acceleration curves for inner ring with different depth faults

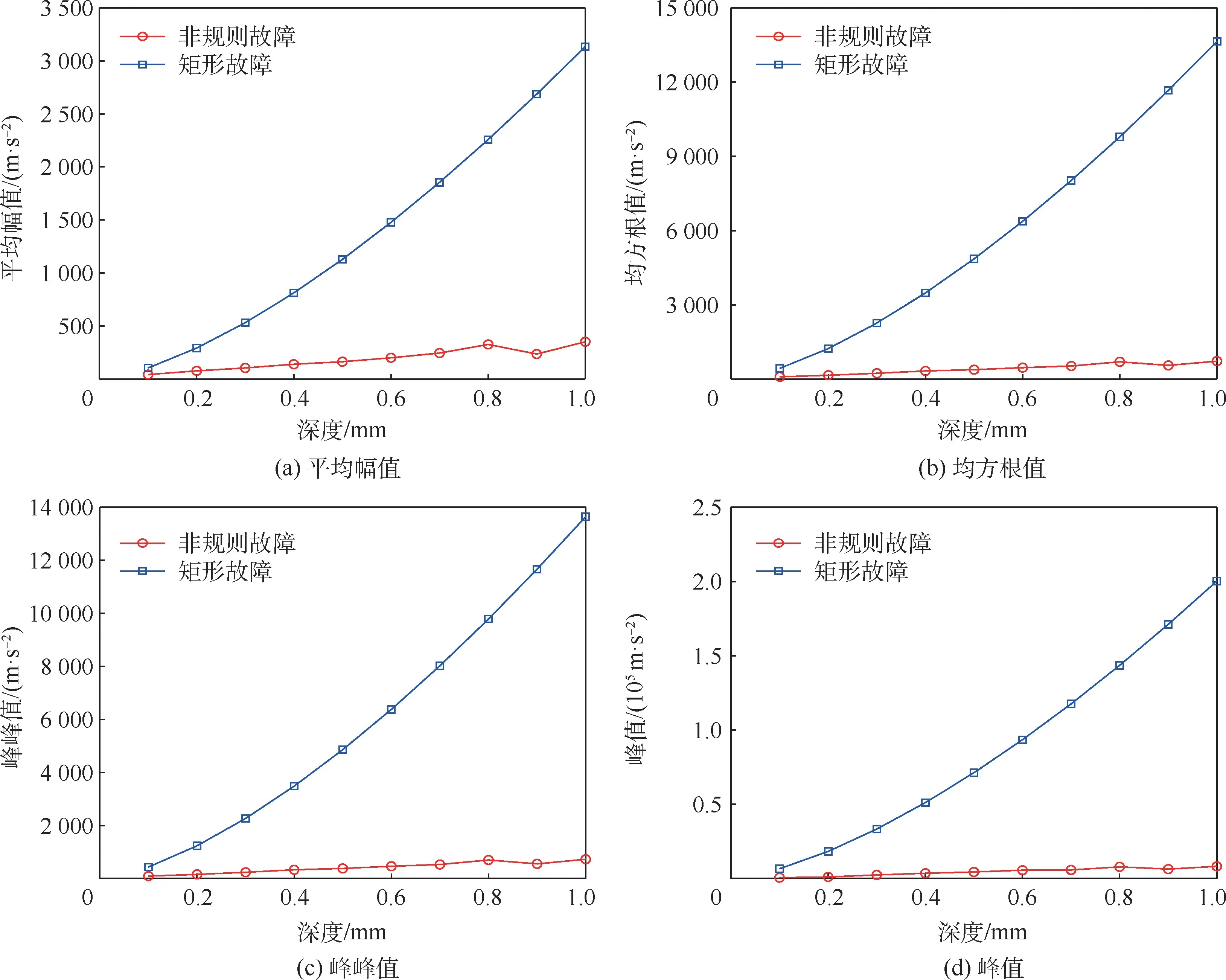
圖17 內圈故障深度對豎直加速度的影響Fig.17 Influence of inner ring fault depth on vertical acceleration

4 試驗與分析

為驗證非規則軸承故障動力學模型的正確性,在轉子系統的右端分別用內外圈含不同故障大小的故障軸承來替代正常軸承。 分別采集軸承內外圈含故障時不同故障大小和不同轉速條件下,系統的位移和加速度振動信號,并對測得的數據進行分析。

4.1 試驗平臺

試驗在清華大學旋轉機械故障綜合模擬試驗臺上進行,其結構如圖18 所示。 轉子系統由變頻電機經聯軸器驅動,轉盤位于兩軸承中間,偏心距為50 mm,偏心質量為10 g。

圖18 綜合模擬試驗臺Fig.18 Integrated simulation test bench

4.2 試件描述

選取2204K 和NJ204E 型軸承為對象,在外圈和內圈滾道上分別采用電火花和線切割加工的方式模擬出周向寬度LD為1 mm、2 mm、3 mm、4 mm、5 mm 的非規則形貌故障,如圖19所示。 試驗時將故障軸承置于轉子系統右端,外圈與軸承座固定,內圈隨著旋轉軸轉動,在不同的轉速下對故障滾動軸承的振動信號進行采集。

圖19 非規則故障形貌Fig.19 Irregular fault topography

4.3 試驗結果與分析

4.3.1 外圈故障試驗

以外圈故障周向寬度LD= 3 mm 的軸承為例,測得其旋轉頻率為10 Hz、30 Hz、60 Hz 時系統振動的響應。 圖20 為轉子的旋轉頻率fr=30 Hz時,外圈故障的仿真信號和試驗信號。 經計算,外圈故障的特征頻率BPFO =131.2 Hz,可以看出仿真信號和試驗信號基本吻合,取得了很好的一致性。 平方包絡譜中都反映了外圈故障的特征頻率和旋轉頻率。

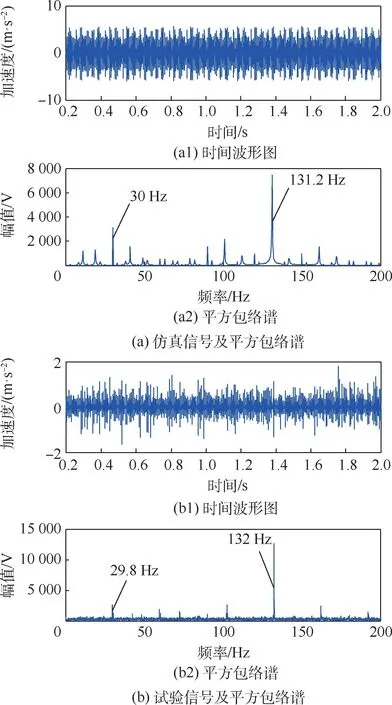
圖20 滾動軸承外圈含非規則故障Fig.20 Rolling bearing outer ring contains irregular faults

圖21 為不同轉速下,轉子右端的振動加速度隨著故障大小變化而變化的曲線。 可以看出,當外圈故障時,轉速越高,滾珠對滾道的沖擊力越大,總體上振動加速度的平均幅值、均方根值、峰峰值和峰值都隨著故障大小的增加而增加,轉速越大,變化越明顯。 當故障達到一定程度時,系統的振動會急劇增大,引起失效,與理論計算結果一致。

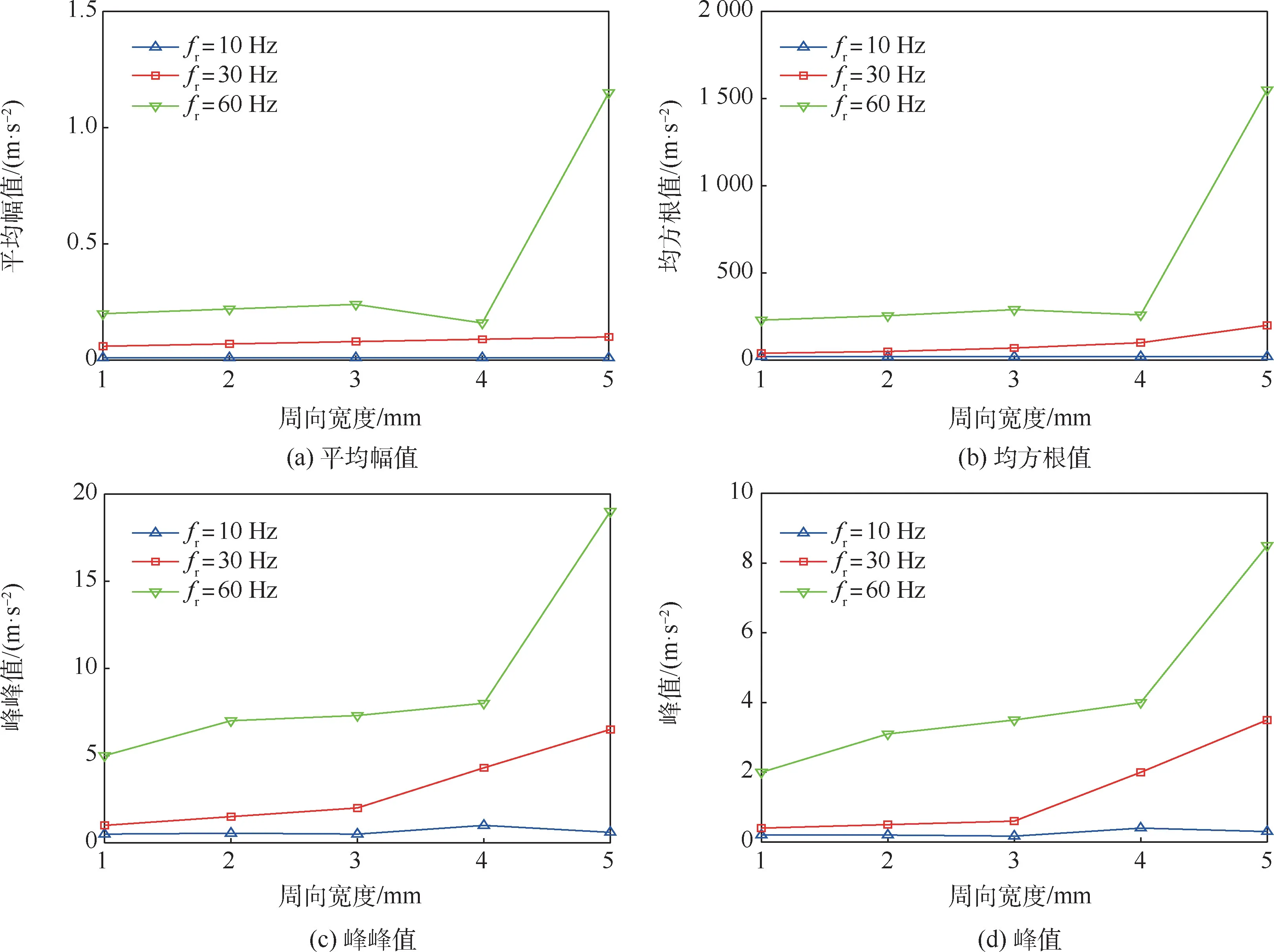
圖21 不同轉速下非規則故障周向寬度對豎直加速度的影響(外圈)Fig.21 Influence of irregular fault width on vertical acceleration at different speeds (outer ring)

4.3.2 內圈故障試驗

以故障周向寬度LD=3 mm 的軸承為例,測得其轉子的旋轉頻率為10 Hz、30 Hz、60 Hz 時系統振動的響應。 圖22 為轉子的旋轉頻率fr=10 Hz時,內圈故障的仿真信號和試驗信號。 經計算,內圈故障的特征頻率BPFI =64.8 Hz,可以看出仿真信號和試驗信號的波形和特征頻率一致性很好,在平方包絡譜中都反映了內圈故障的特征頻率和旋轉頻率。 此外,需要說明的是,轉頻邊帶主要與載荷不均勻產生的幅值調制現象相關,文中載荷相對較均勻,試驗信號中邊頻帶不明顯可能是和試驗臺的振動耦合有關。

圖22 滾動軸承內圈含非規則故障Fig.22 Rolling bearing inner ring contains irregular faults

從圖23 可以看出,當旋轉頻率為10 Hz,與理論計算轉速一致時,所對應的振幅也基本保持不變,與理論計算結果相符。 試驗中由于各種因素的影響,總體來說振動加速度的平均幅值、均方根值、峰峰值和峰值隨著故障周向寬度的增加而增加,但增幅不大,在可接受范圍內,基本與理論計算描述一致。 此外,對于內圈故障而言,在相同的運行條件下,轉速越大,滾珠對滾道的沖擊力越大。 當故障達到一定程度時,系統的振動會急劇增加,引起失效。

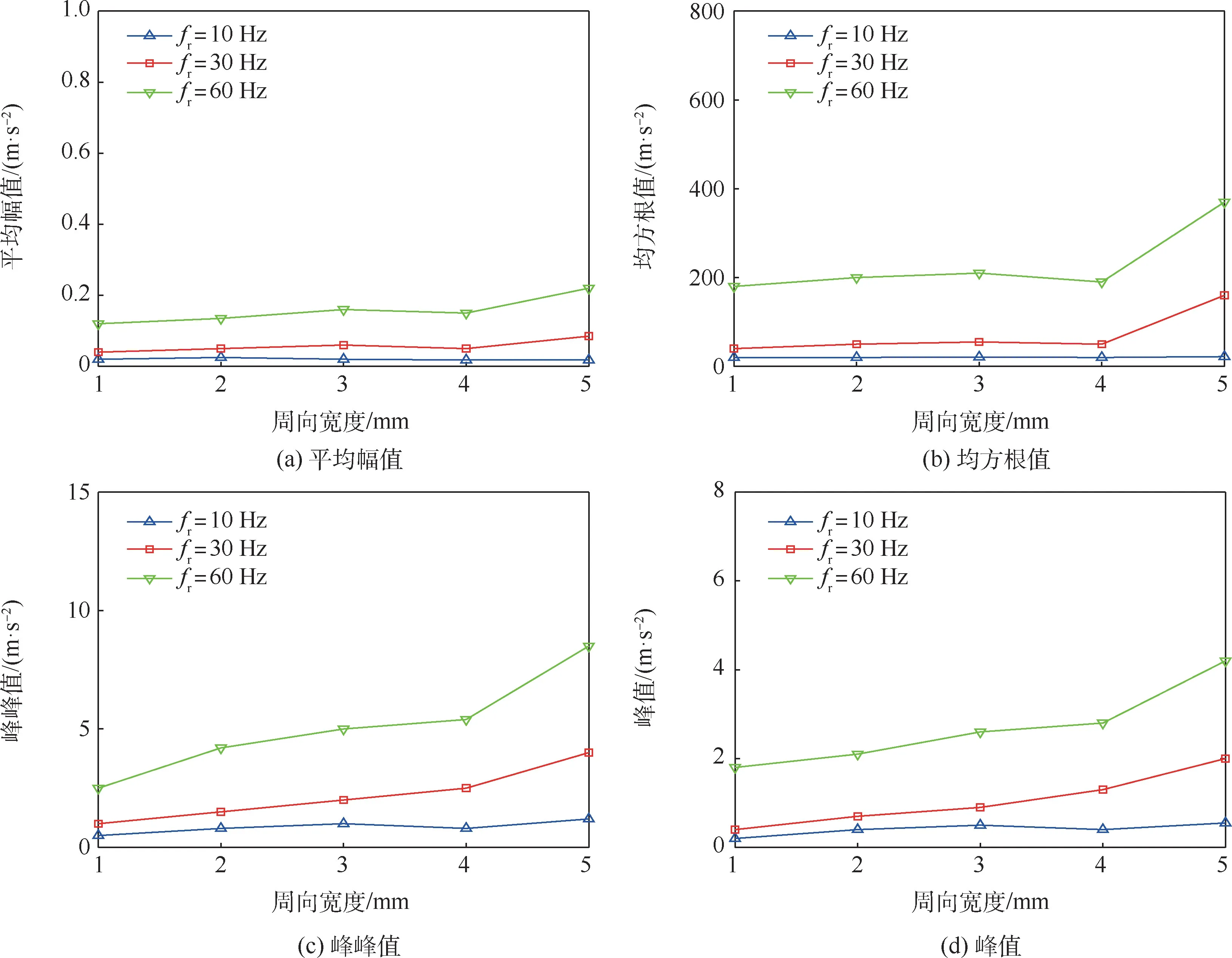
圖23 不同轉速下非規則故障周向寬度對豎直加速度的影響(內圈)Fig.23 Influence of irregular fault width on vertical acceleration at different speeds (inner ring)

5 結 論

1) 軸承非規則故障模型的建立,更加準確地還原了軸承實際損傷時故障表面的形貌特征,減小了滾動體進出故障的瞬時振動影響,反映了滾動體進出故障及通過故障區域時的真實情況,此外還考慮了轉子、軸承之間的耦合,與實際工況更加相符。

2) 軸承內圈含故障時,相同程度的矩形故障所產生的沖擊要明顯高于非規則故障,對于內圈而言,2 種類型故障的周向寬度對于系統振動的影響都不大,而故障深度對系統振動影響十分明顯,隨著故障深度的增加,矩形故障所產生的沖擊強度顯著增加,非規則故障的沖擊強度總體上增加。

3) 軸承外圈含故障時,非規則故障周向寬度大小對系統振動的影響更大,且隨著故障周向寬度的增加而增加,當故障達到一定程度時,系統的振動會急劇增大,引起失效。 這也說明了對軸承外圈而言,非規則故障周向寬度是影響系統振動響應的主要故障參數。 相同的故障周向寬度,隨著故障深度的增加,矩形故障產生的沖擊力更高,沖擊強度顯著增加,非規則故障產生的沖擊強度總體上增加,更加符合實際。

4) 通過對軸承內外圈滾道含故障時系統的振動響應分析,理論上驗證了所提出故障模型的正確性。 通過試驗驗證了數值仿真分析的結果,證明了軸承非規則故障動力學模型的正確性。