基于EMD和SVM 的機載燃油泵故障診斷研究

陳俊柏，劉勇智，陳勇，聶愷

（1.空軍工程大學 研究生院，西安 710038； 2.空軍工程大學 航空工程學院，西安 710038）

飛機的燃油系統作為重要的機載系統，可以為發動機提供符合需求的燃油。燃油泵作為燃油系統的核心部件，是保證系統正常運行的關鍵，一旦在飛行中發生故障，將會對飛機運行的穩定性產生重大影響，可能導致墜機等重大安全事故［1］。因此，為提高飛行的安全性與可靠性，必須采取有效措施對燃油泵故障進行準確的診斷和隔離，以保證飛機健康、穩定地運行［2］。

雖然在機載燃油泵上安裝有壓力傳感器，但是并不能實現對壓力信號的實時采集，在燃油泵發生故障時，無法提供充足的故障數據。并且，由于缺乏有效的故障診斷方法，在燃油泵發生故障后，一般采取拆解或返廠的方式進行維修，其周期長、代價高，會造成巨大的資源浪費。因此，如何節約成本并有效地提高燃油泵故障診斷效率已經得到了國內外的廣泛關注。Muralidharan和Sugumaran［3］利用小波分析提取振動信號的故障特征，并且基于模糊邏輯分類方法實現了燃油泵故障狀態的識別；Tian等［4］選取燃油泵的電流信號作為故障特征信號，通過遺傳算法優化SVM，實現了燃油泵軸承不同損傷狀態的識別；Hancock［5］和Gao［6］等選取燃油泵的壓力信號作為故障特征信號，實現了燃油泵的故障診斷；焦曉璇等［7］針對燃油泵故障特征信號單一，無法充分表現故障特征的問題，通過小波包分析對振動信號和壓力信號進行了故障特征的提取，并利用基于Adaboost算法的BP神經網絡實現了機載燃油泵的故障診斷，提高了多故障模式下燃油泵故障診斷的效率。

針對機載燃油泵振動信號和壓力信號非線性、非平穩的特點，文獻［3，7］分別通過小波分析和小波包分析的方法對燃油泵故障特征進行了較為準確的提取，但是這2種分析方法均存在信號能量泄露、基函數選擇以及不具備適應性的問題。針對機載燃油泵的多故障模式，文獻［7］通過BP神經網絡對其進行識別，但是神經網絡存在對網絡參數依賴程度大以及對結果不可解釋性強的問題［8］。因此，為解決上述問題，提出了一種基于EMD和SVM的機載燃油泵故障診斷方法。

EMD方法是一種信號分解方法，且具備自適應性。EMD方法基于信號的時間尺度，將信號分解為多個表征其局部特點的固有模態函數（IMF）。并且，IMF的頻率特征會隨著采集信號的變化而變化［9］。因此，采用EMD方法作為故障特征的提取方法。

SVM是一種適用于小樣本的機器學習模型，具備堅實的數學理論基礎，對結果具有可解釋性。與傳統的機器學習相比，SVM 泛化能力更強，不存在維數災難的問題［10］。機載燃油泵故障分類問題屬于小樣本、高維模式識別問題。因此，選擇SVM作為機載燃油泵故障的分類模型。

由于SVM性能取決于懲罰參數c和徑向基函數（RBF）參數g的選擇，因此，選擇合適的優化算法對兩者進行優化是十分必要的。網格搜索（GS）算法是一種傳統的參數尋優算法，由于在參數尋優的過程中該算法需要遍歷指定范圍內所有參數，因此GS搜索速度較慢，且容易陷入局部最優解，不利于保證故障診斷的效率。近些年，各種群智能優化算法被廣泛應用于參數尋優，這些算法具備搜索速度較快、精度較高的特點，如粒子群優化（PSO）算法、遺傳算法（GA）、樽海鞘群算法（SSA）等。盡管每一種群智能優化算法擁有各自的優勢，但是群智能優化算法對具體問題應用環境的依賴性比較大［11］，即不同優化算法的性能在具體應用背景下要具體分析。因此，結合采集的機載燃油泵振動信號和壓力信號，在相同的研究環境下，采用PSO、GA、SSA優化SVM 參數，并與GS進行對比分析，來確定SVM參數的優化算法，最終實現機載燃油泵故障的高效診斷。

1 EMD及SVM 方法

1.1 EMD方法

EMD可以分解出信號中不同尺度的波動或趨勢，產生具有不同特征尺度的IMF，IMF分量滿足如下2個條件［12］：

1）IMF的極值點和過零點的個數相同或兩者差值不超過1個。

2）局部極小值和局部極大值會產生2條不同的包絡線，2條包絡線之間所有點的均值都為0。

EMD方法的具體分解步驟如下［13］：

步驟1 確定信號x（t）的所有局部極值點，然后通過3次樣條線分別將所有極大值和極小值連成上、下2條不同的包絡線。由此，所有的數據點均分布在2條包絡線之間。

步驟2 上包絡線與下包絡線之間的任一點均值記為μ1，求出：

步驟3 如果y1（t）不滿足IMF條件，把y1（t）作為原始數據，重復步驟1和2，直到y1（t）滿足IMF條件，此時，記y1（t）＝c1（t），則c1（t）為信號x（t）的第1個滿足IMF條件的分量。

步驟4 將c1（t）從x（t）中分離出來，得到差值信號r1（t），即有

將r1（t）作為原始數據，重復步驟1～3，得到第2個IMF分量c2（t），重復n次，得到n個IMF分量。這樣就有式中：rn（t）為殘余函數，代表了信號的平均趨勢。信號從高頻到低頻的不同成分用本征模態分量c1（t），c2（t），…，cn（t）表示，不同頻段的頻率成分隨信號x（t）的變化而發生相應的改變。

1.2 SVM 方法

假設有訓練樣本｛（xi，yi）｝，i＝1，2，…，N，訓練樣本數為N，分類標簽y∈｛－1，＋1｝，x∈Rm表示m維特征空間。

則超平面為

式中：ω為法向量，決定了超平面的方向；b為位移項，決定了超平面與原點之間的距離。

可以通過求解以下約束優化問題來實現不同類之間的距離最大化，即

對于非線性問題，將特征向量x∈Rm映射到高維歐氏空間，并引入核函數：

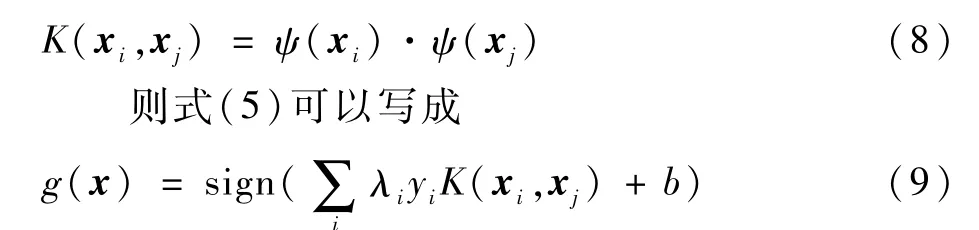
式中：λi為拉格朗日乘子。

2 試驗數據采集及故障模式

機載燃油轉輸系統實驗平臺如圖1所示，各部件主要包括：供油箱、儲油箱、離心式燃油泵、1個壓力傳感器（CY-YZ-001）、3個振動加速度傳感器（CA-YD-182-10）、數據采集設備（億恒MI-7008）等，電機殼相互垂直的3個位置安裝了振動傳感器，如圖2所示。壓力傳感器安裝在燃油泵出口處，如圖3所示。機載燃油泵工作參數如表1所示。

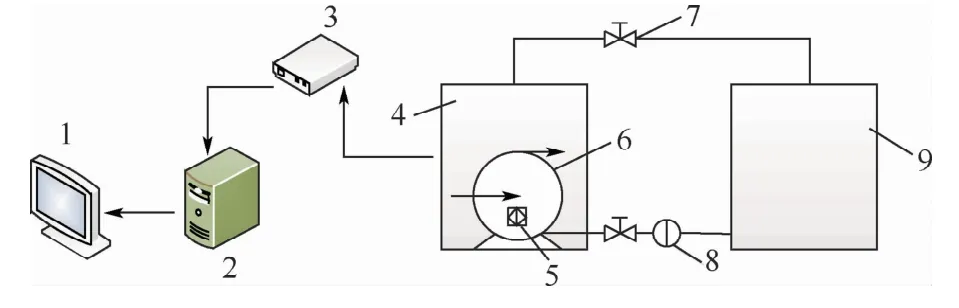
圖1 機載燃油轉輸系統實驗平臺結構示意圖Fig.1 Structureschematicdiagram ofexperimental platform forairbornefueltransfersystem

圖2 振動傳感器實物圖Fig.2 Physicalinstallationofvibrationsensor

表1 產品主要工作參數Table1 Mainworkingparametersofproduct

在測試時，打開閥門，使燃油注入油箱；在油箱中注滿燃油后，打開電源，使燃油泵切換至工作狀態；當燃油泵運行到穩定階段后，對油泵的出口壓力信號以及振動信號進行采集；采集結束后，斷開電源并關閉閥門，使燃油泵逐漸停止工作。由此循環往復，通過更換不同的故障件，獲取相應的故障信號。

通過外場維護的實際經驗發現，葉片損傷、擴散管損傷、密封圈老化導致的滲漏、軸承磨損等都屬于典型故障。實驗針對9類典型故障進行故障診斷的研究，分別為：葉片損傷1片、葉片損傷2片、葉片損傷10片、擴散管損傷、葉片損傷10片加擴散管損傷、滲漏、擴散管與葉輪刮蹭、泵口與葉輪刮蹭、軸承磨損0.02mm。

3 故障特征提取

3.1 振動信號特征提取

以葉片損傷1片為例，圖4為葉片損傷1片的燃油泵故障振動信號。經EMD處理的振動信號共有10個IMF分量，由于處理后的信號能量主要集中在前幾個IMF，因此，圖5僅列出了選取的前4個IMF分量的時域特征，并將這4個IMF分量作為故障特征向量的分量。圖6表示的是葉片損傷1片4個IMF分量的頻域特征。

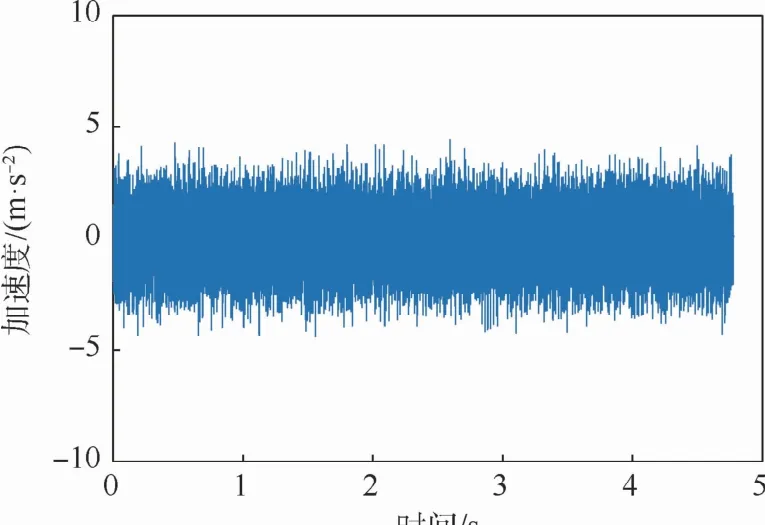
圖4 葉片損傷1片振動信號Fig.4 Vibrationsignalwithonedamagedblade

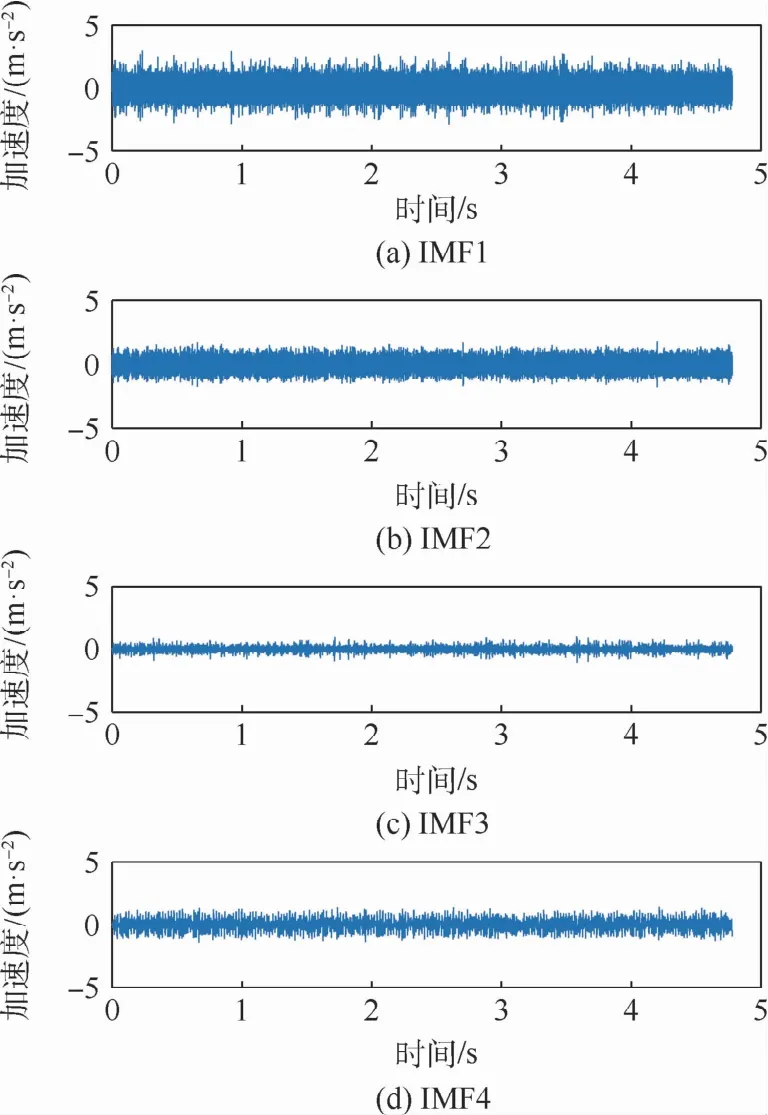
圖5 葉片損傷1片EMD分解Fig.5 EMDwithonedamagedblade

圖6 葉片損傷1片IMF1～4頻域特征Fig.6 Frequency-domainfeaturesofIMF1-4withone damagedblade

重復葉片損傷1片的故障特征提取步驟，可獲得葉片損傷2片的4個IMF分量的頻域特征，如圖7所示。

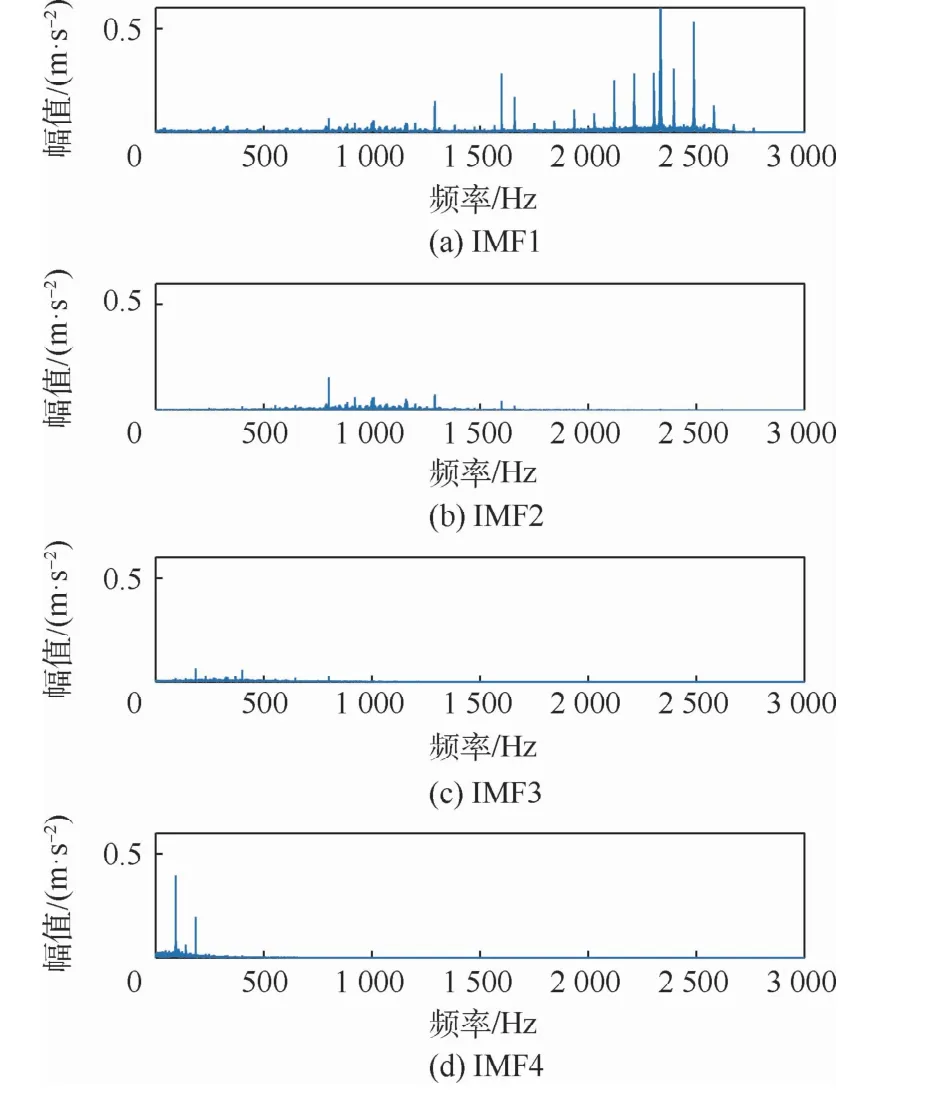
圖7 葉片損傷2片IMF1～4頻域特征Fig.7 Frequency-domainfeaturesofIMF1-4withtwo damagedblades

經EMD分解后的各IMF分量分別代表了一組特征尺度下的平穩信號，由于各分量對應的不同頻帶能量（見表2）表征了燃油泵的不同故障模式，因此，各尺度下IMF分量的頻帶能量可以作為故障特征來識別故障。IMF分量的頻帶能量通過式（10）計算得出

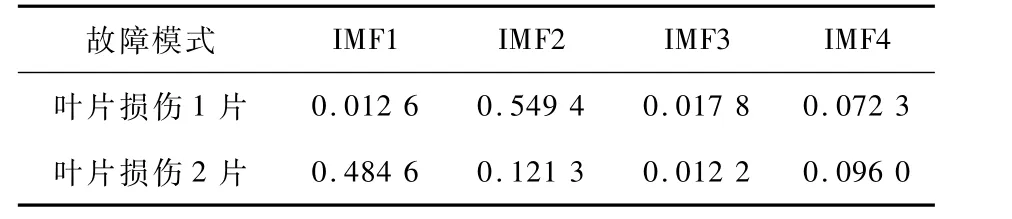
表2 不同故障狀態的歸一化IMF能量Table2 NormalizedIMFenergyindifferentfaultstates

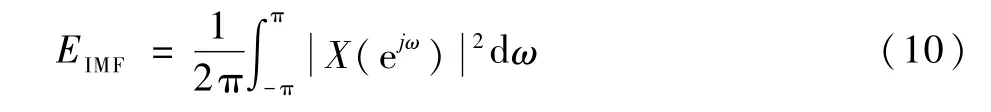
式中：ω為角頻率；X（ejω）為IMF分量的頻域特征。

3.2 壓力信號特征提取

壓力信號能夠在一定程度上反映燃油泵不同的工作狀態。當燃油泵發生不同故障時，壓力信號均值會有所區別。燃油泵壓力信號的正常狀態和幾種典型故障狀態的時域特征如圖8～圖14所示。

圖8 正常狀態壓力信號時域圖Fig.8 Timedomainofpressuresignalinnormalstates

圖14 軸承磨損壓力信號時域圖Fig.14 Timedomainofpressuresignalinwear bearingstate

從表3中可以看出，不同工作狀態下的壓力信號均值在時域范圍內發生了一定程度的變化。因此，可選取壓力信號均值EP作為故障特征，壓力信號均值EP表達式如下：

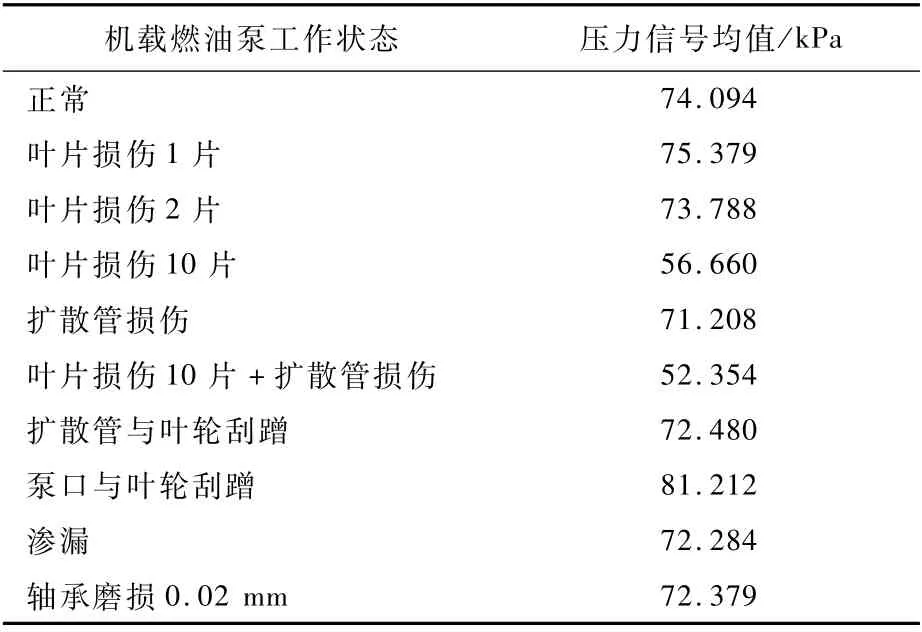
表3 各工作狀態下壓力信號均值Table3 Averagepressureunderdifferent workingconditions

圖10 擴散管損傷壓力信號時域圖Fig.10 Timedomainofpressuresignalwithdamaged diffusiontube

圖11 擴散管與葉輪刮蹭壓力信號時域圖Fig.11 Timedomainofpressuresignalwhendiffusion tubeandimpellerrub

圖12 泵口與葉輪刮蹭壓力信號時域圖Fig.12 Timedomainofpressuresignalwhenpump portandimpellerrub

圖13 滲漏狀態壓力信號時域圖Fig.13 Timedomainofpressuresignalinleakagestate

式中：n為壓力信號的采樣數目；Pk為每個采樣點的壓力值。

4 試驗結果

首先，利用機載燃油泵轉輸系統實驗平臺獲取故障數據，采樣參數如表4所示。

表4 燃油泵數據采集參數Table4 Fuelpumpdataacquisitionparameters

其中，每種工作狀態記錄100組，因此共有1000組故障樣本。為構造故障特征向量，首先利用EMD方法對提取的壓力信號和振動信號進行處理，然后，對故障特征向量進行歸一化處理。表5為燃油泵不同工作狀態下歸一化故障特征參數。

表5 歸一化特征參數Table5 Normalizedpartialcharacteristicparameters

4.1 故障特征選取

由于采集的機載燃油泵故障數據較少，故障特征維數較高，因此，選擇適應小樣本、高維模式識別問題的SVM 作為機載燃油泵故障的分類模型。由于SVM的懲罰參數c與RBF參數g會影響SVM的分類性能，因此通過網格搜索算法對兩者進行優化，以達到較高的故障診斷率。經優化，選取c＝18.3792，g＝97.0059。

首先，僅以壓力信號均值EP作為故障特征，隨機選取并計算機載燃油泵10類不同狀態共800組數據作為SVM 網絡訓練樣本獲得訓練模型（其中，正常狀態80組、葉片損傷1片80組、葉片損傷2片80組、葉片損傷10片80組、擴散管損傷80組、葉片損傷10片＋擴散管損傷80組、擴散管與葉輪刮蹭80組、泵口與葉輪刮蹭80組、滲漏狀態80組、軸承磨損0.02mm80組），訓練樣本編號及分類標簽如表6所示。

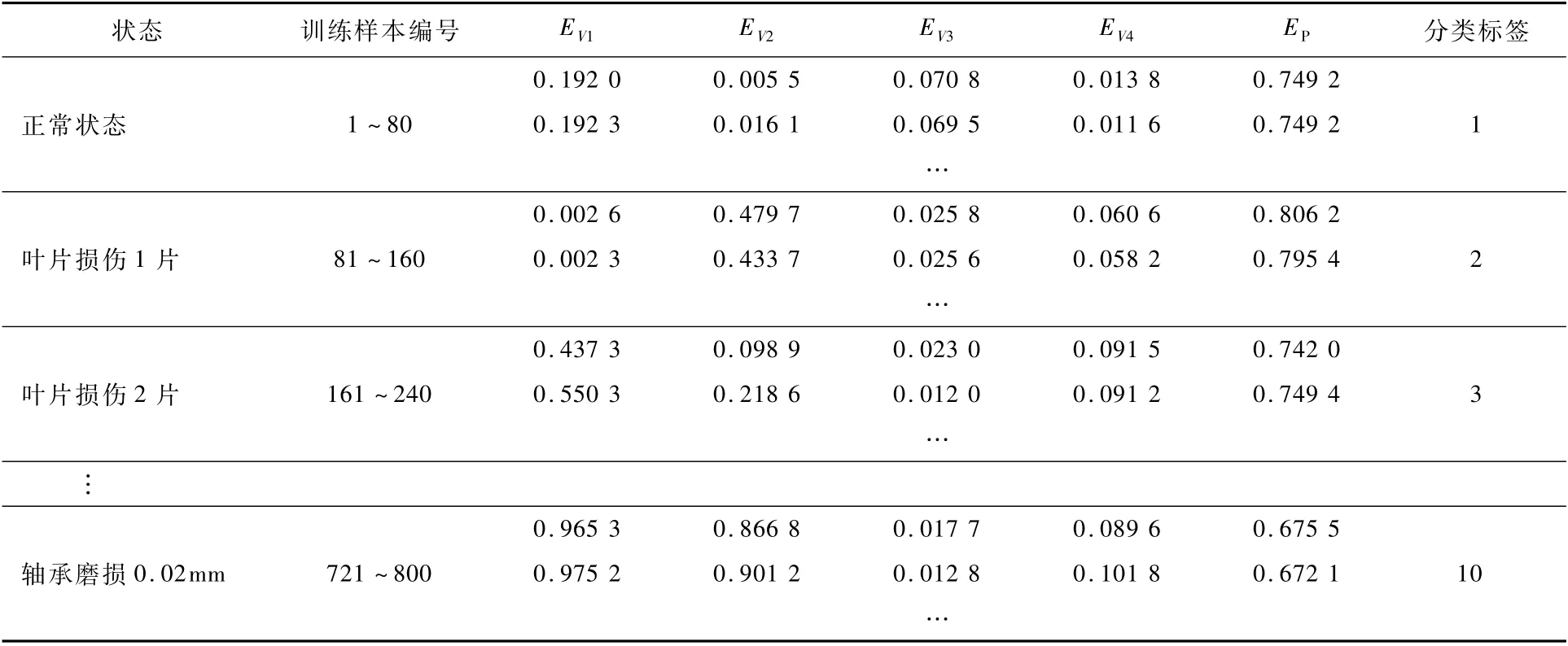
表6 故障特征參數Table6 Faultcharacteristicparameters

之后，將剩余200組數據作為測試樣本輸入訓練模型中（其中，正常狀態、葉片損傷1片、葉片損傷2片、葉片損傷10片、擴散管損傷、葉片損傷10片＋擴散管損傷、擴散管與葉輪刮蹭、泵口與葉輪刮蹭、滲漏狀態、軸承磨損0.02mm 各20組），測試結果如圖15所示，故障診斷率為66.0%（132／200）。

圖15 基于故障特征向量EP 的SVM測試結果Fig.15 SVM testresultsbasedonfaultfeaturevectorEP

隨后，以振動信號IMF能量向量G ＝（EV1，EV2，EV3，EV4）作為特征向量重復上述方法。測試結果如圖16所示，故障診斷率為95.5%（191／200）。

圖16 基于故障特征向量G的SVM測試結果Fig.16 SVM testresultsbasedonfaultfeaturevectorG

最后，以特征向量V＝（EV1，EV2，EV3，EV4，EP）作為特征向量重復上述方法，測試結果如圖17所示，故障診斷率為100.0%（200／200）。

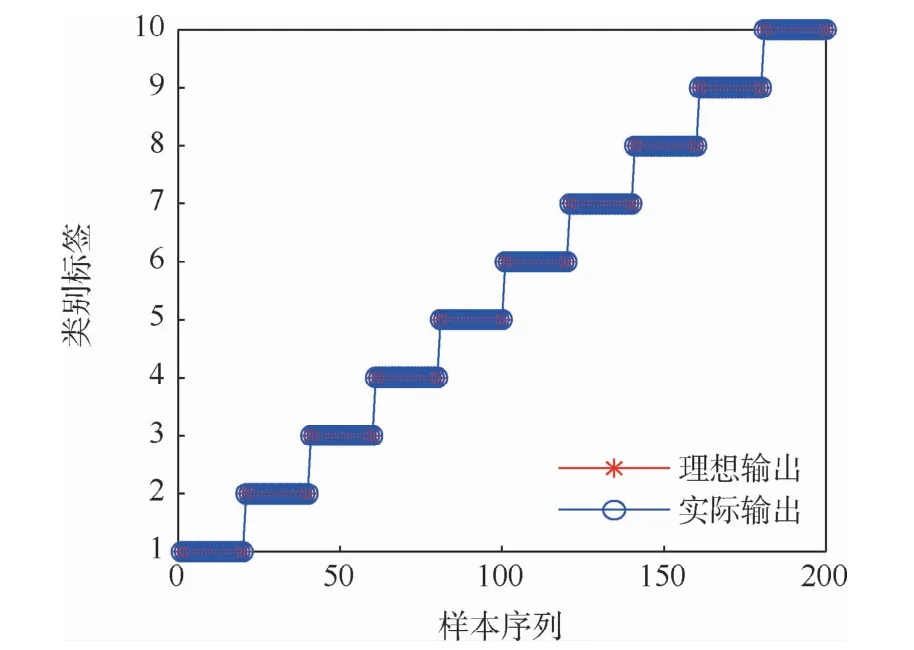
圖17 基于故障特征向量V的SVM測試結果Fig.17 SVM testresultsbasedonfaultfeaturevectorV

由3次實驗結果可以看出，以壓力信號均值EP作為故障特征時，SVM 的故障診斷率較低，僅為66.0%，說明壓力信號均值無法較好地反映各類故障的特征，此時容易出現故障識別錯誤的情況。

以振動信號分解的IMF能量向量G作為故障特征時，SVM 的故障診斷率為95.5%，說明相比于壓力信號來說，振動信號能夠更好地反映燃油泵的故障特征，但是故障診斷率還有待進一步提高。

當使用振動信號IMF能量向量G和壓力信號均值EP組合而成的故障特征向量V時，SVM的故障診斷率為100%，說明相比于前2種故障特征來說，故障特征向量V更能反映機載燃油泵的工作狀態，因此可以選擇向量V作為故障特征。

4.2 故障診斷高效性對比驗證

由于GS在尋優過程中要遍歷所有可能的參數值，導致訓練時間較長，而且容易陷入局部最優解，降低了故障診斷的效率。相較于傳統的尋優算法，群智能優化算法的并行性和分布式特點能夠更快地發現復雜優化問題的最優解。因此，分別采用PSO［14］、GA［15］、SSA對SVM的懲罰參數c和RBF參數g進行優化，并與GS優化的SVM進行對比，其中，群智能優化算法的種群內部個體數為10，終止進化代數為100，懲罰參數c與RBF參數g的范圍均設置在0.1～100之間，評估指標分別為訓練時間和故障診斷率（故障診斷率取20次平均值），結果如表7所示。

表7 算法尋優性能對比Table7 Comparisonofalgorithm optimization performance

由表7可以看出，采用4種優化算法的SVM故障診斷率都比較高，均為100%，說明4種尋優算法均未陷入局部最優解。基于GS的SVM需要遍歷整個搜索空間，訓練時間長，不利于保證故障診斷的效率；基于SSA或者基于PSO的SVM 訓練時間也比較長，同樣不利于保證故障診斷的效率。其中，GA的訓練時間最短，為19.86s，懲罰參數c與RBF參數g分別為9.5531和15.8599。

圖18～圖20為基于3種群智能優化算法的適應度曲線。從圖18可以看出，盡管基于PSO的SVM 最佳適應度從第1代開始就穩定在100%，但是平均適應度在96% ～100%之間波動，體現了尋優的必要性。

從圖19可以看出，基于GA的SVM 最佳適應度和平均適應度從第1代開始就穩定在100%，說明種群中大部分個體屬于“較優個體”，體現了GA“優勝劣汰”尋優機制的特點。

圖19 GA適應度曲線Fig.19 GAfitnesscurves

從圖20可以看出，基于SSA的SVM 最佳適應度和平均適應度從第1代開始就穩定在100%，說明種群中“領導者”和“追隨者”屬于“較優個體”，體現了該算法“追隨”尋優的特點。

綜上，4種優化算法均未陷入局部最優解，故障診斷率均達到了100%。并且，從圖18～圖20可以看出，盡管3種群智能優化算法初始階段的參數隨機性較強，但是依然能夠很快地找到參數的最優解，說明EMD方法提取的故障特征精確度高，降低了SVM中懲罰參數c和RBF參數g的影響。在基于3種群智能優化算法的SVM分類模型中，GA_SVM分類模型的訓練時間最短，可以選擇該分類模型實現機載燃油泵故障的高效診斷。

圖18 PSO適應度曲線Fig.18 PSOfitnesscurves

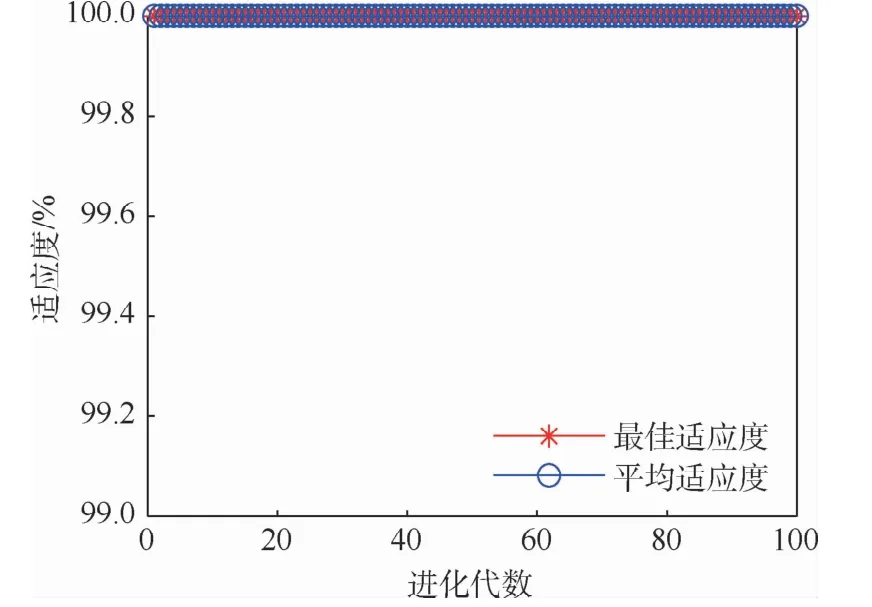
圖20 SSA適應度曲線Fig.20 SSAfitnesscurves

4.3故障診斷準確性對比驗證

分別采用BP神經網絡、極限學習機（ELM）、常規SVM對相同的數據樣本進行訓練與測試，隨機選擇訓練樣本與測試樣本，并和基于GA優化的SVM（GA_SVM）進行比較，評估指標分別為用時（包括特征提取時間和測試時間）、故障診斷率（故障診斷率取20次平均值）、診斷方差（20次測試結果的總方差），結果如表8所示。

表8 各分類器評估指標Table8 Evaluationindexofeachclassifier

由表8可以看出，BP神經網絡用時較長，為3.0000s，不利于保證故障診斷的效率，并且BP神經網絡的診斷方差較高，說明診斷穩定性較低，不利于工程實際的應用。ELM 的故障診斷率較低，為86.95%，不利于工程實際的應用。常規SVM雖然未對懲罰參數c與RBF參數g進行優化，但是診斷方差較低，僅為0.0203，說明EMD方法能夠提取較為準確的機載燃油泵故障特征，使得SVM在不同的懲罰參數c與RBF參數g下仍然保持較高的診斷率，降低了SVM參數對故障診斷率的影響。GA_SVM 的用時短，故障診斷率高，達到100%，診斷方差為0，診斷穩定性較好。

雖然常規SVM 和GA_SVM 在用時、故障診斷率、診斷方差3個方面優勢相當，但是常規SVM沒有對懲罰參數c與RBF參數g進行優化，由于這2個參數在一定范圍內的取值存在偶然性，可能會導致訓練的SVM 模型性能較差，在工程中需要盡量避免這種偶然性，否則會導致診斷效果較差，所以對兩者的優化是十分必要的。

5 結 論

針對機載燃油泵故障數據來源較少、診斷效率較低、維護費用較高、缺乏有效故障特征的問題，設計開發了機載燃油轉輸系統實驗平臺，模擬燃油泵10種工作狀態，監測振動信號和壓力信號，通過時頻特性和統計特性，構造故障特征向量，提出基于EMD和SVM 的機載燃油泵故障診斷方法，結果表明，本文方法可以有效地提取故障特征，并提高故障診斷效率。通過對實驗進行分析和驗證，得到以下結論：

1）壓力信號無法較好地反映機載燃油泵的故障特征，故障診斷準確度較低。而振動信號能夠較準確地反映出機載燃油泵的各種故障特征，故障診斷準確度較高，但還有提升的空間。通過2種信號的結合，故障診斷的準確度得到了進一步的提升。

2）采用3種群智能優化算法的SVM故障診斷率均達到了100%，尋優過程中均未陷入局部最優解，且尋優速度相當。但是在訓練時間上，GA優于其他3種算法，從節約計算資源以及時間耗費上考慮，可以選擇GA對SVM 參數進行優化，提高機載燃油泵故障診斷效率。

3）SVM的故障診斷率和診斷穩定性均高于人工神經網絡，證明了SVM在小樣本、非線性、高維模式識別問題的優勢。