一道涉及三角形面積的中考題的多種解法

摘 要:對于平面直角坐標系中任意三角形面積的計算,利用割補法進行巧妙、創造性的構造,通過圖形形狀的轉換使得三角形面積的計算變得簡捷、容易.文中的幾種構造思路開闊了眼界,為傳統解法注入了新的活力.
關鍵詞:拋物線;三角形面積;割補法
中圖分類號:G632????? 文獻標識碼:A????? 文章編號:1008-0333(2021)26-0030-02
收稿日期:2021-06-15
作者簡介:徐新賢(1962-),男,本科,中學高級教師,從事中學數學教學研究.[FQ)]
拋物線內接三角形的面積計算問題是中考中的常考題型,由于其綜合性較強,給一些同學帶來了一定的困惑.通常一道質量較高的考試題,其解法大都不會是單一的,其對優秀學生與普通學生的區分往往體現在對解題方法的選擇上.而把握題目特點并尋求較簡潔的解法對培養學生們發散性思維及模型歸納能力有一定幫助.本文以2017年湖北孝感市的中考壓軸題第24題為例提出多種解法,以啟發中考復習課堂高效復習的思路.例 (簡化版)在平面直角坐標系xOy中,規定:拋物線y=a(x-h)2+k的伴隨直線為y=a(x-h)+k.如圖1所示,頂點在第一象限的拋物線y=mx-12-4m與其伴隨直線相交于點A、B(點A在點B的左側),與x軸交于點C、D.如果點P(x,y)是直線BC上方拋物線上的一個動點,△PBC的面積記為S,當S取得最大值27/4時,求m的值.
此題的解題思路是這樣的:先求出點B、C的坐標,然后寫出△PBC的面積表達式,從而得出m的值.
首先應該明確題目中的一個隱含條件,即圖1給出的拋物線開口向下,意即m<0.(為了敘述方便,下面分五個步驟進行求解)
(1)求點B的坐標.
∵拋物線的解析式為y=m(x-1)2-4m,
∴其伴隨直線方程為y=mx-1-4m=mx-5m,
聯立以上兩式得mx-1(x-2)=0,即得x=1或x=2,把x值代入拋物線的伴隨直線方程得y=-4m或y=-3m,∴A1,-4m,B(2,-3m).∵m<0,∴A、B兩點均在第一象限內.
(2)求點C的坐標.
把y=0代入拋物線方程可得x-1=2,即x=-1或x=3,∴C-1,0,D(3,0).
(3)畫出△PBC.
先描出B、C兩點,連接BC,然后在BC上方的拋物線上任意取一點P(x,m(x-1)2-4m),連接PB、PC得到△PBC,如圖2所示.
(4)寫出△PBC的面積表達式.
注意到此題的實質是求平面直角坐標系中任意三角形的面積,常用的方法是在原圖形的基礎上通過添加與坐標軸平行(垂直)的輔助線,構造出(我們常說的割補法)容易計算面積的規則幾何圖形,從而算出任意△PBC的面積.常見有以下幾種處理方法.
方法1 補成直角梯形
如圖2所示,過P、B、C三點作坐標軸的垂線,補成直角梯形CQEB,則
S△PBC=S梯形CQEB-S△CQP-S△PEB=12(yP+yP-yB)xB-xC-12yPxP-xC
-12xB-xP(yP-yB)
=3m2x2-x-2=3m2(x-12)2-27m8
方法2 補成矩形
如圖3所示,過P、B、C三點作坐標軸的垂線,補成矩形CQEF,
則
S△PBC=S矩形CQEF-S△CQP-S△PEB-S△CBF
=3m2x2-x-2
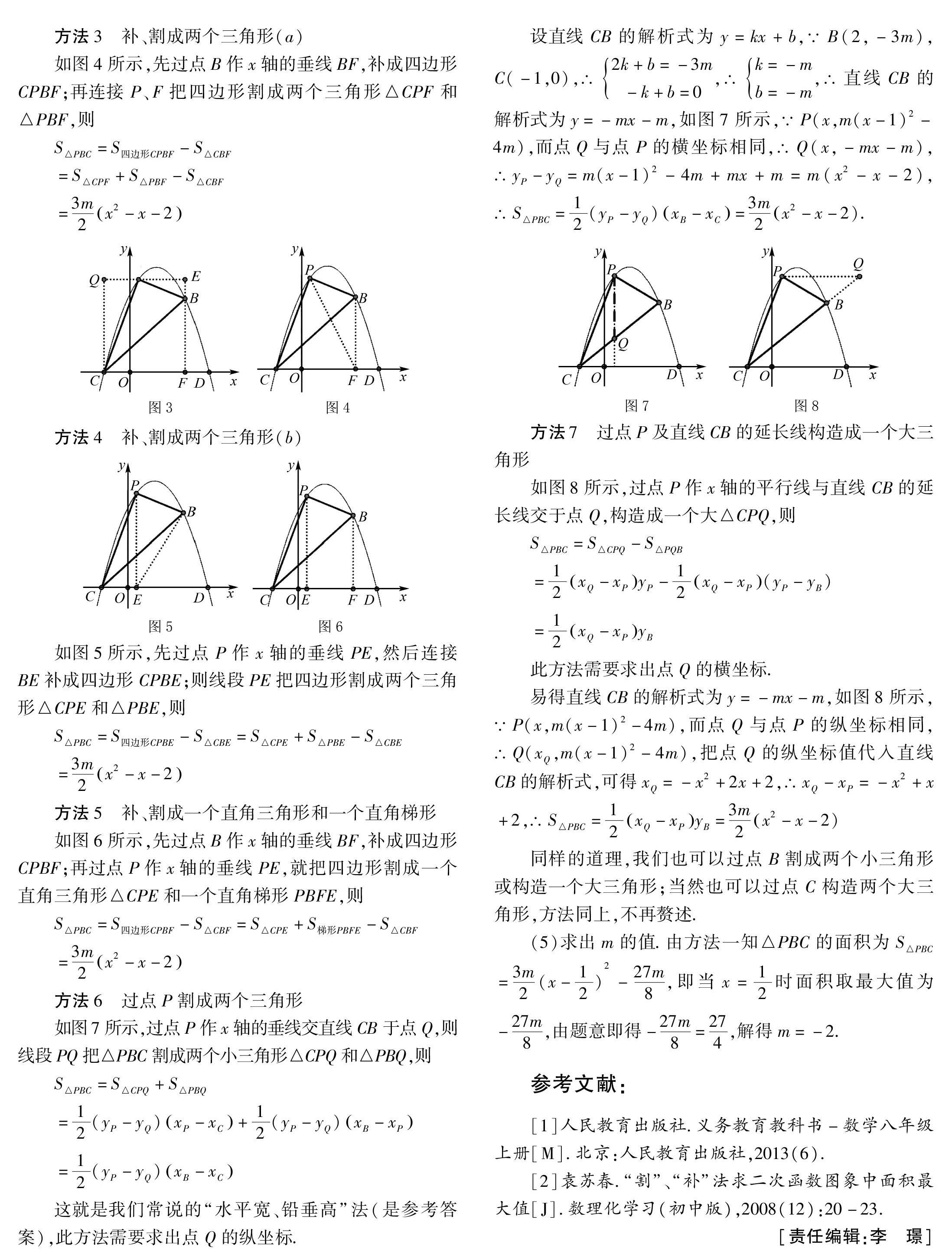
方法3 補、割成兩個三角形(a)如圖4所示,先過點B作x軸的垂線BF,補成四邊形CPBF;再連接P、F把四邊形割成兩個三角形△CPF和△PBF,則
S△PBC=S四邊形CPBF-S△CBF
=S△CPF+S△PBF-S△CBF
=3m2x2-x-2
方法4 補、割成兩個三角形(b)
如圖5所示,先過點P作x軸的垂線PE,然后連接BE補成四邊形CPBE;則線段PE把四邊形割成兩個三角形△CPE和△PBE,
則
S△PBC=S四邊形CPBE-S△CBE=S△CPE+S△PBE-S△CBE
=3m2x2-x-2
方法5 補、割成一個直角三角形和一個直角梯形
如圖6所示,先過點B作x軸的垂線BF,補成四邊形CPBF;再過點P作x軸的垂線PE,就把四邊形割成一個直角三角形△CPE和一個直角梯形PBFE,
則
S△PBC=S四邊形CPBF-S△CBF=S△CPE+S梯形PBFE-S△CBF
=3m2x2-x-2
方法6 過點P割成兩個三角形
如圖7所示,過點P作x軸的垂線交直線CB于點Q,則線段PQ把△PBC割成兩個小三角形△CPQ和△PBQ,則
S△PBC=S△CPQ+S△PBQ
=12(yP-yQ)xP-xC+12(yP-yQ)xB-xP
=12(yP-yQ)xB-xC
這就是我們常說的“水平寬、鉛垂高”法(是參考答案),此方法需要求出點Q的縱坐標.
設直線CB的解析式為y=kx+b,∵B(2,-3m),C(-1,0),∴2k+b=-3m-k+b=0,∴k=-mb=-m,∴直線CB的解析式為y=-mx-m,如圖7所示,∵P(x,m(x-1)2-4m),而點Q與點P的橫坐標相同,∴Q(x,-mx-m),∴yP-yQ=m(x-1)2-4m+mx+m=m(x2-x-2),∴S△PBC=12(yP-yQ)xB-xC=3m2x2-x-2).
方法7 過點P及直線CB的延長線構造成一個大三角形
如圖8所示,過點P作x軸的平行線與直線CB的延長線交于點Q,構造成一個大△CPQ,
則
S△PBC=S△CPQ-S△PQB
=12xQ-xPyP-12xQ-xP(yP-yB)
=12xQ-xPyB
此方法需要求出點Q的橫坐標.
易得直線CB的解析式為y=-mx-m,
如圖8所示,
∵P(x,m(x-1)2-4m),而點Q與點P的縱坐標相同,∴Q(xQ,m(x-1)2-4m),
把點Q的縱坐標值代入直線CB的解析式,可得xQ=-x2+2x+2,
∴xQ-xP=-x2+x+2,
∴S△PBC=12xQ-xPyB=3m2x2-x-2)
同樣的道理,我們也可以過點B割成兩個小三角形或構造一個大三角形;當然也可以過點C構造兩個大三角形,方法同上,不再贅述.
(5)求出m的值.
由方法一知△PBC的面積為S△PBC=3m2(x-12)2-27m8,
即當x=12時面積取最大值為-27m8,
由題意即得-27m8=274,解得m=-2.
參考文獻:
[1]人民教育出版社.義務教育教科書-數學八年級上冊[M].北京:人民教育出版社,2013(6).
[2]袁蘇春.“割”、“補”法求二次函數圖象中面積最大值[J].數理化學習(初中版),2008(12):20-23.
[責任編輯:李 璟]

