澳元和加元匯率的聯動性研究
——基于DCC-GARCH模型
金劍峰
一、DCC-GARCH模型
DCC-GARCH(動態條件相關GARCH)模型由Engle和Sheppard(2001)建立。他們認為,時間序列的波動性隨著時間推移不斷變化,且與前期波動大小相關,具有異方差性。DCC-GARCH模型假定收益率的波動與前期波動相關,引入條件方差自身的滯后項作為影響因子,減少了待估參數。與多變量GARCH模型相比,實用性更強,可以清晰動態地呈現波動間的關系。DCC-GARCH模型的基本形式如下:
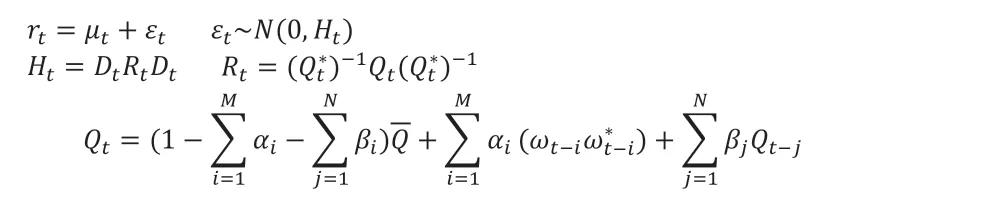
其中,εt為收益率的殘差項;Ht為正態分布的條件協方差矩陣;Dt為根據單變量GARCH模型所計算出的條件元素K×K對角矩陣;Rt為動態條件相關系數矩陣;Qt為標準化殘差的無條件相關矩陣;為Qt的對角矩陣;為ωt的非條件相關系數矩陣;ωt為向量標準化殘差;αi為第i項資產的標準化無條件協方差系數;βj為協方差矩陣系數。
二、實證分析
1.描述性統計
我們分別使用澳元對美元的匯率和加元對美元的匯率作為研究對象,根據國際外匯市場慣例,澳元匯率使用間接標價法,加元匯率使用直接標價法。數據來源為wind金融數據終端。選取數據的時間區間為1978年10月2日至2021年1月14日,同時考慮到澳大利亞和加拿大的節假日不一致的問題,只要有一國存在節假日,則刪除當日相應外匯交易數據,最終保留10985個日收盤數據。為了保證數據的平穩性,我們將價格序列轉換為對數收益率序列,考慮到兩種貨幣匯率標價方法的不一致,我們在轉換時都按照直接標價法來計算,由此各得到10984個數據。
從收益率序列的時間趨勢可以看出,澳元和加元收益率序列的偏度均為負,峰度均大于3,呈現尖峰厚尾特征;JB統計量均通過1%的顯著性檢驗,因而兩個收益率序列均不服從正態分布。澳元和加元匯率的收益率序列均表現出明顯的波動聚集性。
2.平穩性檢驗
對澳元和加元收益率序列進行ADF單位根檢驗,ADF統計值分別為-105.1067和-105.6229,在1%的顯著性水平下均拒絕原假設,收益率序列不存在單位根,是平穩序列。
3.均值方程及GARCH模型的建立
首先對收益率序列進行自相關和偏自相關檢驗,確定選擇何種形式的均值方程。從自相關檢驗結果看,在澳元和加元收益率序列分別滯后1~3階和1~4階的情況下,不能通過5%的顯著性檢驗,因而兩個收益率序列并不存在明顯的自相關關系。因此,我們將GARCH模型的均值方程設定為白噪聲,設立模型為:rt=μt+εt。
將兩個收益率序列分別減去各自的均值,得到w_aud和w_cad。再對這兩個新的數列分別求平方,得到w2_aud和w2_cad。分析w2_aud和w2_cad的自相關性。結果表明這兩個數列arch效應顯著,存在自相關。所以,均值方程的設定是合適的,可以用GARCH模型進一步估計。針對澳元和加元的收益率序列分別建立GARCH(1,1)模型,得到的系數均通過了1%的置信度檢驗,并且ARCH項與GARCH項系數相加小于1,這表明模型的整體擬合效果良好。
澳元和加元匯率之間的相關性是否隨著時間的推移而發生變化?這種變化是否存在規律?為了回答這個問題,我們需要在GARCH(1,1)模型的基礎上,采用多變量GARCH模型對澳元和加元的相關性做進一步分析。為了建立DCC-GARCH模型,我們將條件方差模型設定為GARCH(1,1),ARCH項和GARCH項的滯后階數分別設為1階。計算得到a值為0.015516,b值為0.983195,a和b都通過了1%的置信度檢驗,并且a+b<1,說明均值方程的設定是正確的,模型擬合比較理想。一般說來,a+b的值越接近于1,說明兩者之間的動態相關關系越明顯,也就是說,澳元和加元的收益率序列之間存在持續而顯著的相關關系。
圖1直觀地呈現出1978年10月2日至2021年1月14日澳元和加元匯率的動態相關系數。可以發現,澳元和加元之間的動態相關系數隨時間推移而不斷發生變化,但極少出現負值。此外,還可以看出2007年是一個大致的時間窗口,從這一年開始澳元和加元匯率之間的聯動性顯著增強了。
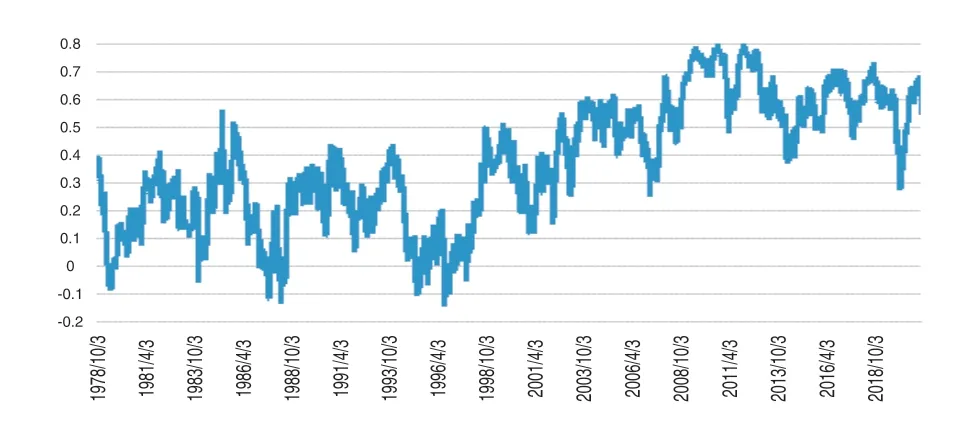
圖1 加元和澳元的動態相關系數(DCC)圖
三、結語
本文采用DCC-GARCH模型,考察了澳元和加元匯率相關性的動態變化,據此可以得出兩個結論:首先,澳元和加元匯率之間存在較強的正相關性,且相關系數呈現動態時變性特征。原因在于,澳大利亞和加拿大同為自然資源比較豐富的國家,農產品和礦產品的出口占比較高,受到全球經濟和貿易因素的影響較大,動態聯動性效應明顯。其次,自2007年以來,澳元與加元匯率的聯動性更為顯著。其原因是,一方面,美國次貸危機及后續政策對澳元和加元的影響基本相同;另一方面,國際經貿合作不斷加深,進一步強化了各國經濟聯系,盡管次貸危機的影響已經逐漸消散,但澳元和加元依然表現出很強的聯動效應。

