數方格的策略研究

鄭麗君

中圖分類號：A 文獻標識碼：A 文章編號：（2021）-34-494

學生在學習《平行四邊形的面積》之前，三年級下冊已經學了《面積與面積單位》、《長方形與正方形的面積》。如果說長方形面積公式是所有面積公式的老祖宗，那么平行四邊形面積計算公式則起了承上啟下的作用。因為這是轉化的開始，是學生在“轉化”意識驅動下剪拼方法的初次嘗試。

若想順利完成初次轉化，一定要牢牢抓住方格的作用。也許有教師會認為數方格是三年級的水平，太簡單了，五年級還要數方格嗎？不排除有教師會棄之不用。與之相反，我認為，數方格不僅不簡單，而且蘊含著大大的道理。

因為面積教學要從數方格開始，借方格理解面積概念，借方格完成轉化。

一、方格的重要地位

1、面積單位與方格的關系

人教版三年級下冊，在帶領學生探索面積單位的過程中，深刻體會到用正方形作為面積單位的合理性，既密鋪又利于計算數量的多少。之后教學的1平方厘米、1平方分米、1平方米的大小都用正方形去刻畫。所以，在面積教學中，方格和面積單位是緊密結合在一起的。

2、用面積單位度量長方形面積

人教版三年級下冊，在探究長方形和正方形面積時，用一個個小方格去擺滿長方形，再數出一共有幾個小方格，讓學生深刻地感受到長方形的面積是用一個個小方格去度量的，如同量長度是用尺子度量一樣。所以，作為面積單位的方格，是面積教學中的一把“二維尺子”，可見它的作用不可小覷。

3、借方格喚舊知

人教版五年級上冊，在平行四邊形面積教學中，再次使用了方格。查閱各版本教材，在平行四邊形面積教學中，無不把數方格安排在前面打頭陣。數方格在這里起到了兩個重要作用，一是對單位面積和面積測量的回憶，這種回憶能為平行四邊形的面積計算提供豐富的感性材料，從而使學生獲得面積計算的意義支撐;二是對長方形面積公式推導過程的回顧，從直接度量到間接度量，從一維到二維的想象。

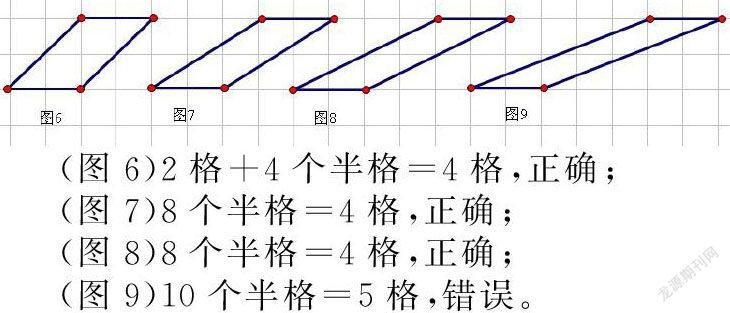
二、“不滿一格的都按半格計算”合理嗎？

數方格對于學生來說不是第一次遇到，但此次數方格與學習長方形面積時數方格不同，這次出現了不完整格。在困難面前，學生要解決的問題是怎樣才好數？教材提示，“不滿一格的都按半格計算”。這樣編寫的目的也許是為了幫助學生解決新問題，提供策略指導。但是“不滿一格的都按半格計算”這樣的規定合理嗎？

如果都按“不滿一格的都按半格計算”的規定去數平行四邊形面積會有怎樣的結果出現呢？

通過以上面積相同形狀不同的平行四邊形的對比，我們會發現“不滿一格的都按半格計算”這句話是有局限性的。這個規定只有滿足以下三個條件才能成立：

1、線段圍成的圖形。

2、線段的端點都在方格線的交點上。

3、從方格線的交叉點連線段，只要不出現“三分格”即可。（三分格：一個格被線段切割成三部分稱為三分格。）

那些不符合的圖形都是因為出現了“三分格”。

查閱了不同版本的教材，除了我們使用的人教版外，蘇教版教材在編寫時也作了這樣的規定。但其目的是不一樣的。不規則的曲線圖，不滿格之間是不能直接拼組的。所以，蘇教版作這樣的規定，既是為學生提供了解決問題的策略，又包含了估算意識的培養。而其他版本都沒有這樣的規定。

三、數方格再處理

人教版數學五年級上冊“平行四邊形的面積計算”，教材中呈現讓學生通過數方格得出平行四邊形的面積，在數的過程中，學生就遇到了難題：有不滿半格的或大于半格的怎么辦？教材指出“不滿一格按半格算”，大多學生不明白為什么不滿半格能按半格算。如果不提示，又可以怎么做呢？

教師可以改為提問：誰能用最快的方法數出平行四邊形的面積？這就逼著學生先數滿格的，再數不滿格的，而不滿格的那么多，怎么辦？這里要留給學生充足的時間，讓學生經歷困難，通過觀察發現，左邊的不滿格剛好與右邊相應的不滿格拼成一格，學生通過湊零為整初步感知移拼的轉化方法。依據學生思維層次和空間觀念的不同，拼的方法和次數各不一樣，有的需要拼四次、三次完成，有的兩次可以拼成，甚至還可以一次拼成的......

接著，再次引導學生觀察整個左邊的不滿格都可以與右邊的不滿格拼成滿格，拼成后的圖形是不規則的，算起來還是不太方便，學生在教師的啟發下，進一步發現可以把整個左邊的方格移到右邊，就可以拼成一個長方形，這樣的數方格就是最便捷的方法，學生進一步體驗轉化的重要意義，同時得出平行四邊形的面積=底×高。

這樣的鋪路引導，學生的探索就有了明確的方法，在不斷滲透和體驗中，學生對平行四邊形轉化為長方形的方法有了真正的理解和應用。這一環節既有一定的挑戰性，又能充分調動學生已有的知識經驗，初顯方格魔力。

四、觀點與啟示

“數方格”這一內容的教學不僅是求面積的一種策略，更重要的是加深了學生對“面積”概念的理解。

而“不滿一格按半格計算”的規定，既存在定義上的局限性又約束了學生的探究之路。所以，本人拙見，這個規定應該刪去。放手讓學生去探究，他們的體會才會更加深刻，數學烙印才會真正烙在他們自己的心里。