死亡率風險對壽險公司估值的影響探究
邢 辰 南開大學金融學院

一、引言
隨著經濟發展水平和衛生醫療水平的不斷提高,我國人口的總體平均預期壽命也有逐年提高的趨勢。根據國家衛健委發布的《2019年我國衛生健康事業發展統計公報》,我國的人口平均預期壽命已經從2018年的77.0歲提高到2019年的77.3歲。各年齡死亡率不斷下降的趨勢無疑會導致保險產品價值的波動,從而影響保險公司估值的準確性,最終影響經營決策。
目前國內外的相關研究主要關注死亡率風險的衡量和管理手段。學術界對死亡率風險管理手段的研究主要分為兩種:
第一種是自然對沖手段,即利用死亡率變化對壽險和年金產品影響方向相反的特點,合理配置兩種產品以規避風險。Jeffrey(2009)用CBD 模型擬合死亡率,設定目標函數為使損失波動的條件風險價值(CVaR)最小,并加入了利潤約束的條件,來決定銷售產品的最優化配比。Jennifer(2010)使用Lee-Carter模型來擬合死亡率,并采用死亡免疫的方法計算最佳壽險—年金產品組合比例,以規避壽險公司面臨的長壽風險。Wang(2013)假設保險公司的資產組合由無風險債券、壽險保單和年金保單組成,資產組合的價值變化同時受利率風險和死亡率風險的影響,得出了可以最小化其變化幅度的最優產品組合。在國內相關研究中,李冰清(2016)應用CBD模型刻畫隨機死亡率,并在償付能力的約束下探究保險公司在不同產品線上的最優資本配置。
第二種是風險管理手段,即利用死亡率相關衍生品,如長壽債券、長壽互換等,來實現死亡率風險的管理。Wong(2017)采用雙隨機復合泊松過程對保險負債建模,研究了保險公司使用長壽債券或長壽互換的動態均值差異對沖問題,并推導出了最優對沖策略。國內的相關研究中,艾蔚(2011)探討了利用死亡率相關的衍生工具管理死亡率風險的可行性,并對比分析了不同衍生品的風險管理有效性。
除了死亡率風險的衡量和管理,國內外在死亡率風險的影響方面的研究分析也取得了一定進展。Jeffrey 等(2000)分析探討了死亡率風險對壽險公司年金產品的躉交保費可能產生的影響,研究認為壽險公司在為年金產品厘定費率時需要充分考慮未來死亡率可能存在的改善趨勢。Gründl(2006)以股東價值(SHV)最大化為目標,分析了死亡率風險對保險公司的最佳風險管理組合(權益資本、資產配置和產品政策)的影響。Gatzert(2012)采用自然對沖的風險管理方法,量化了死亡率變化對壽險公司違約風險的影響。文章認為,為了更深入地了解自然對沖對保險公司風險狀況的影響,同時考慮資產和負債兩方面是非常重要的。Nadine(2014)分析了自然對沖、死亡率衍生品兩種風險管理手段對不同類型死亡率風險的有效性。Anton.S(2019)從股東和被保險人兩個角度,研究了德國壽險公司資產組合中應用自然對沖策略對權益頭寸產生的影響。國內的相關研究主要集中在死亡率風險對產品的保費厘定及準備金產生的影響。祝偉(2012)研究發現,未來死亡率的改善會明顯提高個人年金業務的支付現值,從而對定價和準備金管理產生影響。謝漫锜等(2013)擬合了不同性別各年齡死亡率的改善情況,并分別探究了死亡率改善對于壽險和年金產品責任準備金變動情況的影響。孫佳美(2014)利用Monte Carlo 方法模擬了未來死亡率,并在模擬死亡率和靜態死亡率假設下分別探究責任準備金風險的變化情況,研究發現,死亡率的改善會明顯改變產品準備金的分布及波動情況。
然而,現有關于死亡率風險影響的研究大多數局限于產品層面或單純的公司風險管理層面,沒有考慮到公司估值的因素。而在實務中,無論是從公司內部、股東還是監管角度出發,壽險公司估值的準確性都非常重要。如果死亡率風險影響了公司實際估值,公司內部可能會做出錯誤的長期經營決策;股東方面有可能會被偏差的公司估值誤導而蒙受損失;估值不準確也可能導致監管機構錯誤評級,影響公司長期發展。
鑒于此,本文將死亡率風險和公司估值兩個方面的因素同時納入考量,為壽險公司風險管理提供新的視角。研究將基于兩個方面:一是對未來不同年齡人口死亡率的合理建模、擬合和預測;二是在固定死亡率和預測死亡率假設下研究公司估值的分布情況。為了簡化分析,本文假設死亡率風險是壽險公司的全部風險來源,也就是說,在本文框架下我們不再考慮信用風險、市場風險等其他風險因素。本文采用CBD模型擬合不同年齡人口的死亡率數據并在此基礎上進行預測,探究在不同死亡率假設的框架下,壽險公司價值的波動情況。本文的創新之處在于,將死亡率風險和公司估值因素聯系到一起,為壽險公司的估值和風險管理提供了全新視角。
二、模型設計
(一)未來死亡率擬合模型:CBD模型
CBD 模型包含了兩個時間效應參數,可以用于對隨機死亡率進行擬合和預測,最早由Cairns等(2006)提出。CBD模型的基本表達式結構如下:

其中,t為離散時間;x是年齡;為x歲的人在t到t+1期間死亡的概率。模型里的兩個因子A1(t)和A2(t)代表了所有年齡面臨的死亡率隨時間推移的改善情況,其中A1(t)隨時間推移逐漸下降,其作用是以相同程度改善所有年齡的死亡率;而A2(t)為正值,其作用是使得死亡率隨時間的改善程度因年齡段的不同而有所差別,其中低齡人群的死亡率隨時間的改善更為明顯。這兩個因子同時代表了死亡率隨時間變化的改善趨勢效應和年齡差異效應。當我們考慮因子隨時間的參數變化時,CBD模型將具有經濟或生物學意義。
進一步地,為了預測A(t)=(A1(t),A2(t))'的未來分布情況,CBD模型把A(t)假設為帶有漂移項的二維隨機游走:
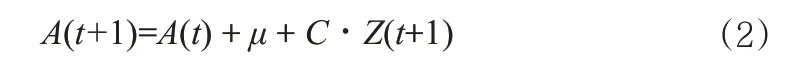
其中,μ為2×1的常量矩陣;C為一個2×2的上三角矩陣,從半正定矩陣V=C?C'分解而來;Z是二維標準正態隨機變量。
Cairns 等(2006)令D(t)=A(t)-A(t-1),并通過非信息性的先驗分布,證明了μ,V滿足normal-inverse-Wishart分布。
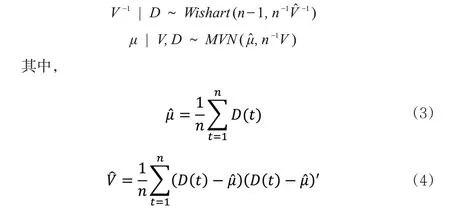
根據以上信息,本文即可對未來死亡率進行擬合和預測,并進一步對公司估值情況進行探究。
(二)公司估值模型:內含價值法
壽險公司的產品往往期限較長,而當期利潤主要來自之前保單的剩余邊際釋放,因此無法簡單地用當期會計利潤來衡量公司運營狀況或評估公司價值。鑒于此,本文將使用行業內常用的內含價值法來作為公司估值模型。
內含價值法(Embedded Value)的相關概念最早由Anderson 提出。他認為,由于壽險行業資產和負債存在特殊性,壽險公司的真正價值不能用一般企業的估值方法來合理反映,而是應該綜合考慮全部有效保單以及新業務保單在未來可能創造的價值。Bangert(1973)在Anderson(1959)思想的基礎上詳細解釋了“有效業務價值”和“新業務價值”的定義并給出兩者的計算方法,同時他也認為,可以利用未來現金流折現加總的思想來衡量壽險公司的真實價值。隨著相關理論不斷發展,歐洲部分國家開始要求壽險公司在其年報內必須報告其內含價值。國內的相關應用起源于2005 年原保監會發布的《人身保險內含價值報告編制指引》,文件中首次提出了壽險公司進行內含價值評估的強制要求。隨著中國償二代框架不斷完善,2016 年中國精算師協會發布《精算實踐標準:人身保險內含價值評估標準》,進一步要求我國壽險公司應當充分具備準確評估內含價值的能力。
內含價值模型的基本思想是,壽險公司真實價值應該等同于公司現有凈資產的總價值與未來預期會實現的收益現值的和。其簡要表達式如下:
評估價值(AV,Appraisal Value)=內含價值(EV)+新業務價值(VNB,Value of New Business)
其中,內含價值被定義為公司持有資產的市場價值+公司保單的有效業務價值-公司持有要求資本的成本,這里的有效業務價值是指公司當前有效保單預計可以產生的、最終將歸屬于股東所有的現金流的現值;新業務價值則被定義為評估日前一年簽發的所有保單未來預計產生的股東現金流的現值。
本文的后續部分將假設公司原本沒有任何有效保單,所有保單將在初始時刻作為新保單同時售出,故在本文研究框架下不存在有效業務價值。為簡化研究,本文將使用新業務價值指標代表公司估值。
在評估時點T,公司的新業務價值等于未來各期預計可分配盈余現值扣除評估時點的要求資本。其表達式如下:

1.要求資本RC(Required Capital),是為了滿足監管機構對保險公司提出的償付能力要求而必須留存的資本量。在內含價值模型框架下,RC可以表示為:
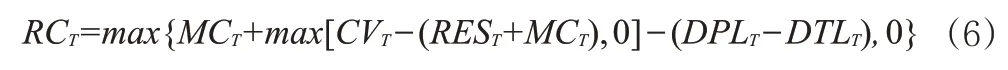
其中,MC(Minimum Capital)為監管機構要求公司持有的最低資本(Minimum Capital),由各子風險的預測資本載體乘以對應的最低資本預測因子,并通過一定方式匯總得出;CV(Cash Value)為保單的現金價值;RES為保單的準備金(Reserve);DPL為保單的剩余邊際(Deferred Profit Liability),來源于首日利得的攤銷,可以用攤銷載體和攤銷因子相乘得出;DTL為剩余邊際對應的應交稅金。因DTL=DPL×稅率,故DPL-DTL為稅后剩余邊際。
2.未來可分配盈余DE(Distributable Earnings),等于公司業務的稅后凈利潤和可投資凈資產所得收益的總和。DE可以被表示為:
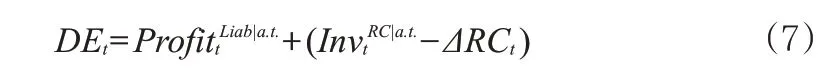
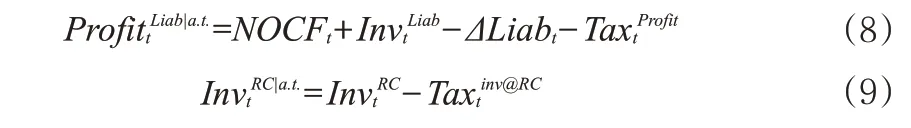
式(8)中,NOCFt為凈經營現金流的最優估計,為準備金投資收益,ΔLiabt為壽險業務負債提轉差(Liabt-ΔLiabt-1),為所得稅支出。式(9)中,可投資凈資產的稅后投資收益則由要求資本的投資收益扣減相關稅費()計算得出。需要注意的是,在償二代假設框架下,壽險業務負債應該等于法定準備金(RES)與剩余邊際(DPL)的和。
根據上述信息,把未來各期可分配盈余的表達式整理如下:
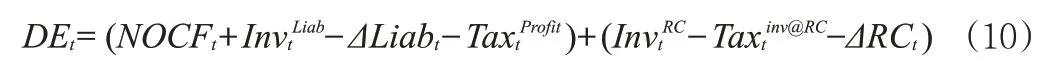
3.風險貼現率RDR(Risk-adjusted Discount Rate),被定義為將風險因素納入考量范圍后經調整得出的貼現率,用于計算未來可分配盈余的折現值。
由此,通過式(5)(6)(10),我們便可以計算出公司的新業務價值,并以其作為本文中壽險公司價值的合理預估。
三、參數假設及研究步驟
(一)數據來源及處理
本文使用我國1994—2019 年共計26 年的30 歲及以上男性經驗死亡率的相關數據,并合理使用CBD 模型進行擬合。數據來源于1995—2006年《中國人口統計年鑒》、2007—2020年《中國人口與就業統計年鑒》,以及《中國2000年人口普查資料》和《中國2010年人口普查資料》。
原始數據中多數年份的年齡組別為30~89歲各年齡和90歲及以上,因此本文采取同樣的年齡分組方式,并對少數年份的數據進行調整。其中,1995年、2000年、2005年、2010年、2015年死亡率數據的年齡組別為30~99歲各年齡和100歲及以上,本文將這些年份中90歲及以上各年齡的平均人口數和死亡人口數分別加總并手工計算得出90歲以上年齡段的死亡率;1996年死亡率數據的年齡組別為30~84歲各年齡和85歲及以上,本文采取鄰年線性插值的方法計算此年85~89歲各年齡和90歲及以上組別的死亡率。
(二)產品組合及相關參數設定
1.壽險公司產品組合設置
本文將產品組合設定為壽險公司主要出售的兩種典型產品:壽險和年金,全面考察死亡率的未來變動對公司估值可能造成的影響。由于死亡率相關數據的年齡最高組別為90 歲及以上,無法保證該組別各年齡模擬未來死亡率的準確性,因此本文將目標險種設置為定期壽險和遞延定期年金,具體設定如表1所示。
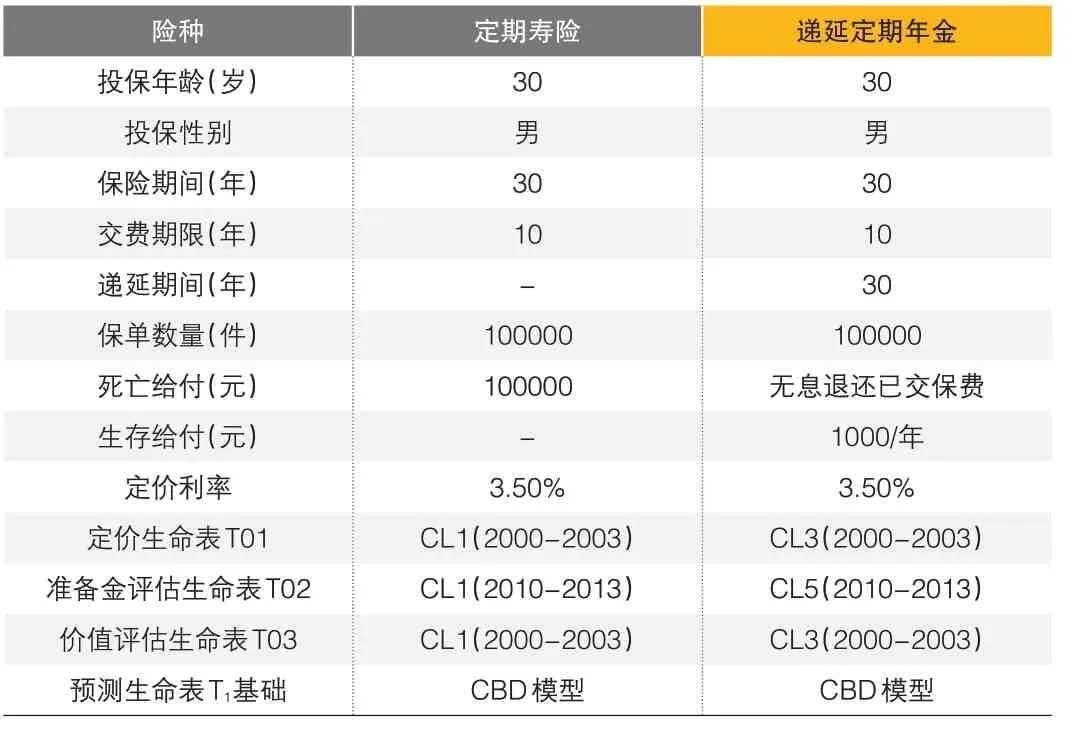
?表1 壽險公司產品組合設置及其相關參數
2.公司價值評估有關假設及其參數設置
本文將在償二代假設下進行公司價值評估過程。需要注意的是,由于本文重點在于考察死亡率風險對公司價值評估的影響,因此在計算各期要求資本時將只在模型中納入死亡風險,而忽略信用風險等償二代框架中包括的其他風險。根據償二代下壽險公司新業務價值評估的一般原則和經驗假設,本文設置了相關參數,如表2所示。
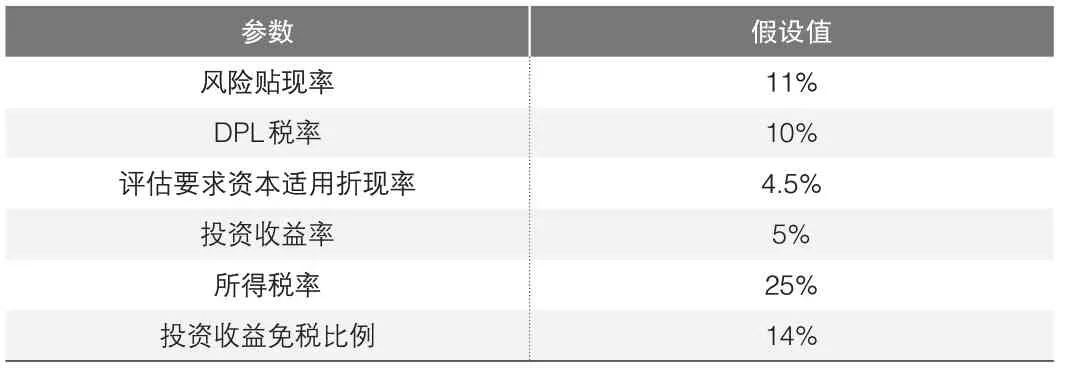
?表2 公司價值評估相關參數設置
(三)研究步驟
產品定價過程中如果沒有充分考慮到未來死亡率的改善趨勢,保費可能會被高估或低估,從而影響公司估值的準確性。鑒于此,本文首先根據行業內普遍使用的生命表對兩種產品進行定價和估值,再模擬不同死亡率假設下公司估值的波動情況。具體研究步驟如下:
1.對兩種產品分別建模,在給定生命表T01和T02的假設下對其定價和評估準備金。
2.在價值評估階段,首先設置初始保單數量,并假設死亡人數是關于給定生命表T03 的二項分布,模擬出各年齡的死亡人數,結合步驟1 中的保單價格及準備金,得出在此情境下的產品價值;將此步驟重復10000 次,即可得出給定生命表T03 假設下的公司估值波動情況。
3.以CBD 模型為基礎,模擬出10000 張預測生命表,并取其期望值,作為預測生命表T1。
4.用預測生命表T1替換給定生命表T03,把步驟2重復10000次,即可得出預測生命表假設下的公司估值波動情況。
5.在步驟2 和步驟4 得出公司估值的兩種分布情況的基礎上,分別計算其期望值、標準差、偏度、峰度、VaR值和CVaR值,并通過對比兩種情境,來探討死亡率風險對壽險公司估值的準確性及波動情況可能產生的影響。
四、基本結果
(一)基于CBD模型的隨機死亡率預測
本文利用CBD模型和最小二乘法,根據式(1)擬合我國1994—2019年30歲及以上男性經驗死亡率數據,參數估計結果如圖1所示。
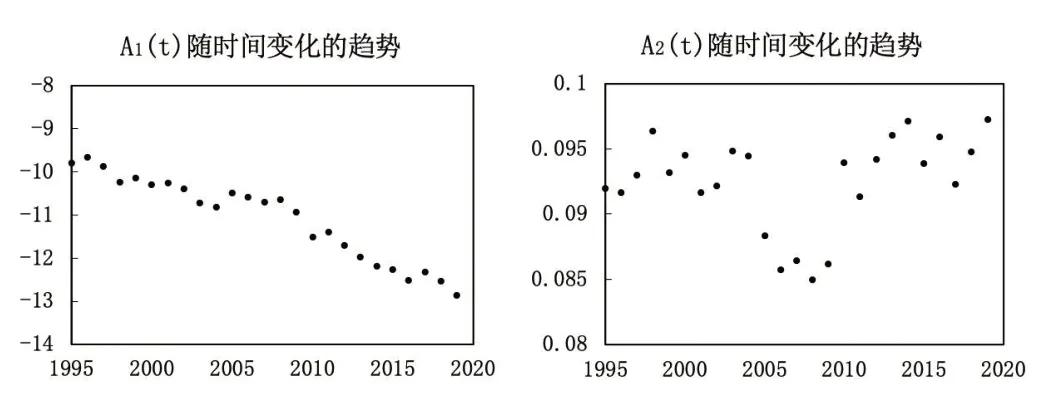
?圖1 CBD模型擬合結果
從圖1可以看出,A1(t)隨時間推移有逐漸下降的趨勢,這表明各年齡死亡率隨時間推移整體有所改善;A2(t)則存在不規則的波動趨勢,且估計值都是正值,這表明隨著時間推移,各年齡死亡率的改善情況并不相同,即年齡越大,其死亡率隨時間的改善效果就越弱。

(二)不同死亡率假設下的公司價值評估分析
1.給定生命表下的公司價值評估分析
本文對兩種產品分別建模,首先在給定生命表的假設下模擬了兩種產品新業務價值和公司價值的波動情況,其分布直方圖如圖2和圖3所示。同時,本文也計算了三者模擬分布的期望值、標準差、偏度、峰度、VaR和CVaR值,以便于后續的定量探討,具體結果如表3所示。
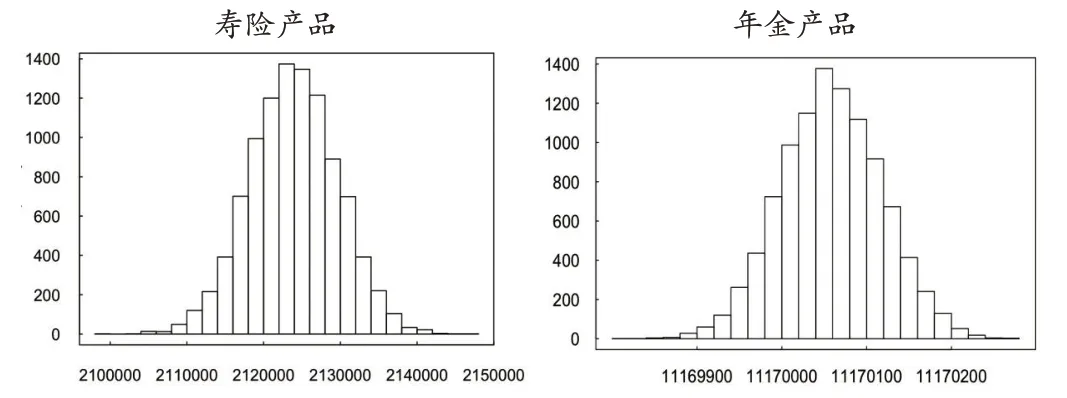
?圖2 給定死亡率下兩種產品新業務價值分布情況(單位:元)
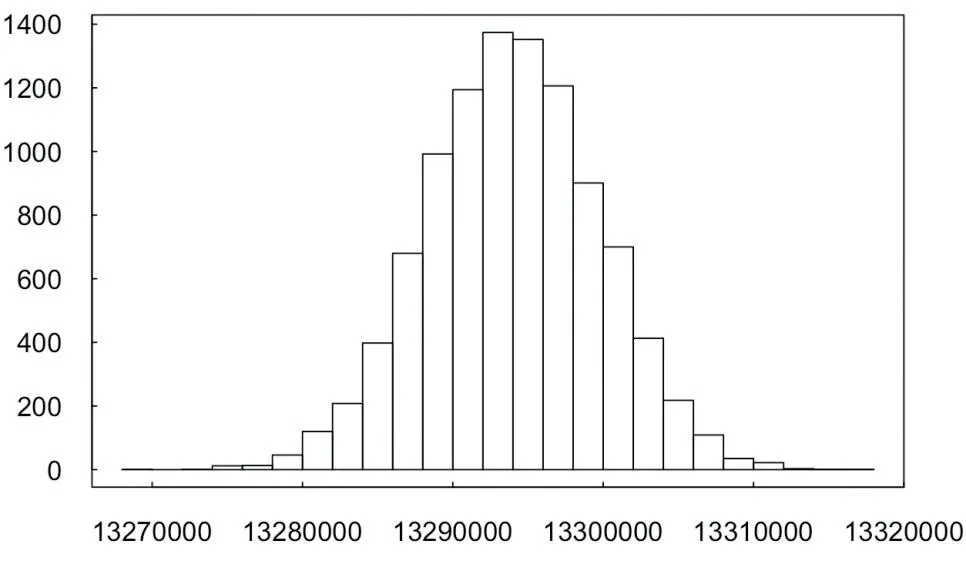
?圖3 給定死亡率下公司價值分布情況(單位:元)
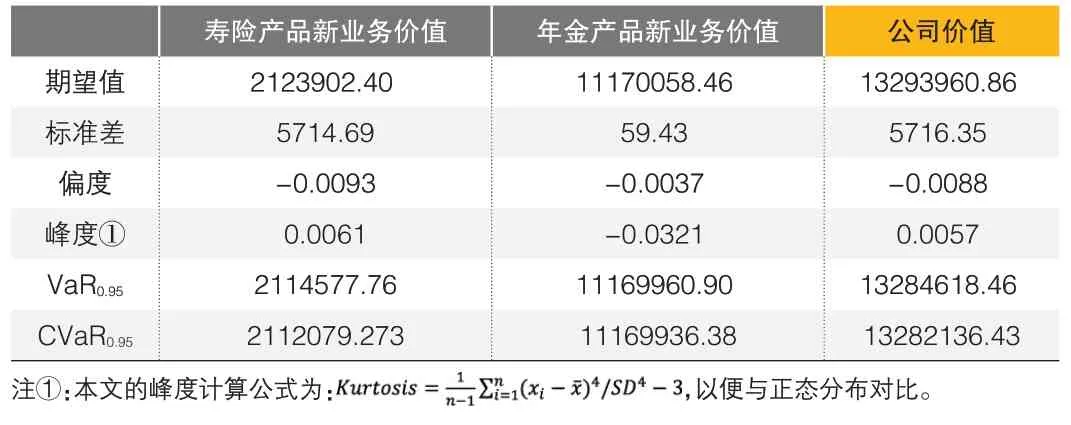
?表3 給定生命表下的公司價值波動分析(單位:元)
從圖2和圖3中可以看出,雖然兩個險種的保障內容不同,但當實際死亡率圍繞給定死亡率波動時,兩個險種的新業務價值均會受到影響,導致公司價值也出現波動,其分布接近于正態。
下面根據表3 進行具體分析。三種分布圍繞期望值有不同程度的波動,各自的偏度和峰度均接近于0,即分布情況均近似于正態;VaR0.95和CVaR0.95均為正值。值得注意的是,壽險和年金產品的新業務價值標準差分別為5714.69 和59.43,即在給定假設下,死亡率波動導致的壽險產品新業務價值波動幅度明顯大于年金產品。這可能是因為本文設定的年金產品同時包括生存給付和死亡給付,而兩者受死亡率變動的方向相反,起到了對沖作用,因此年金產品的新業務價值相對穩定。但因受到壽險產品的影響,公司價值的波動仍較為明顯。
2.預測生命表下的公司價值評估分析
為了考察死亡率的改善對公司實際價值產生的影響,我們使用CBD模型擬合并預測未來死亡率,以此建立預測生命表,并基于預測生命表及其波動,重新評估兩種產品的新業務價值及對應的公司價值,其分布直方圖如圖4和圖5所示。我們同樣給出了預測生命表假設下三者模擬分布的期望值等主要統計指標,具體結果如表4所示。
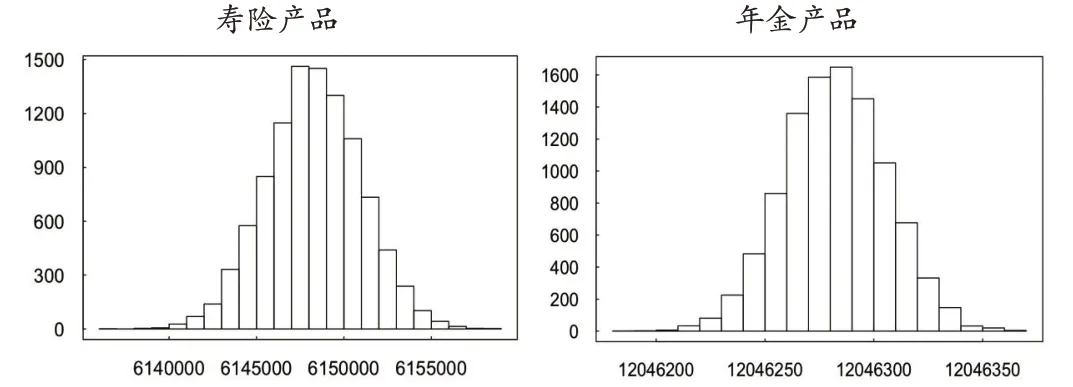
?圖4 預測死亡率下兩種產品新業務價值分布情況(單位:元)
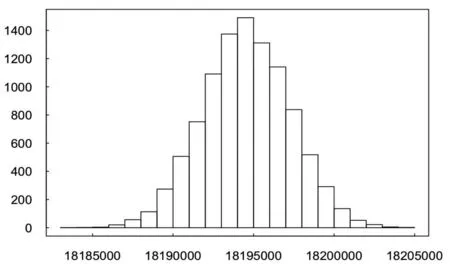
?圖5 預測死亡率下公司價值分布情況(單位:元)
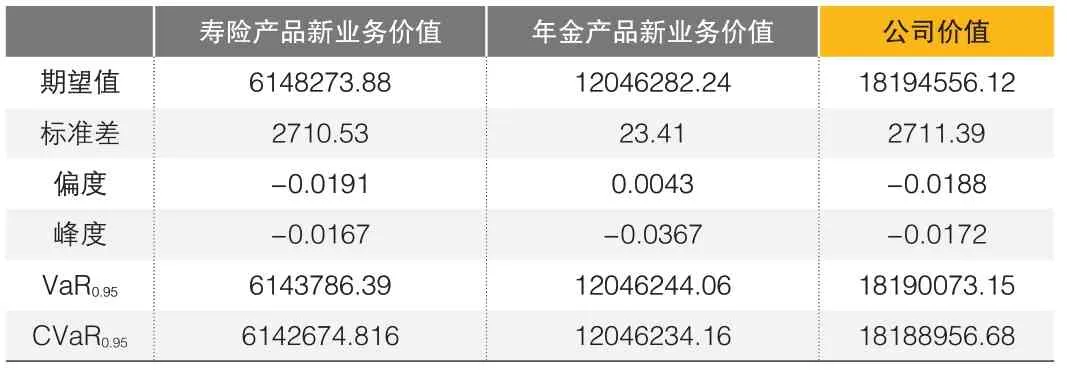
?表4 預測生命表下的公司價值波動分析(單位:元)
從上述結果可以看出,當考慮到死亡率的改善時,兩種產品新業務價值和公司價值的偏度和峰度與表3相比沒有太大變化,仍然接近正態分布;但三者的期望值、VaR0.95、CVaR0.95都有不同程度的提高,這意味著在給定死亡率下,無論是兩種產品新業務價值還是公司價值都被明顯低估了。此外,三者模擬分布的標準差都有所降低,這意味著估值時如果充分考慮了死亡率改善,就可以使公司價值的波動幅度相對減小,有利于公司長期穩定經營。
3.不同死亡率下公司價值分布對比分析
對于壽險產品來說,死亡率的改善意味著未來死亡賠付的現值會降低,因此,如果估值時未考慮死亡率的改善,則會低估壽險產品的新業務價值。而對于年金產品來說,死亡率的改善一方面意味著預期壽命延長,生存給付的現值會提高;另一方面年金產品中死亡給付現值則會降低。因此,當年金產品中同時包括生存給付和死亡給付時,其新業務價值受到死亡率改善的影響方向并不確定,取決于兩種變動方向的總效應。在本文的假設下,壽險產品的新業務價值變動非常明顯,其期望值比給定死亡率下的期望值高出189%;年金產品新業務價值的變動幅度則相對較小,其期望值比給定死亡率下的期望值高出7.84%,這意味著死亡率的改善會導致兩種產品的新業務價值同時被低估。兩者加總后,公司價值的期望值則比給定死亡率下的預估價值高出36.86%,這意味著在本文框架下,如果壽險公司估值時沒有把未來人口死亡率可能存在的改善趨勢充分納入考量,評估出的公司價值將比其真實價值降低近30%。
由此可知,未來死亡率的改善會顯著影響壽險公司估值,如果不采取措施修正估值時的死亡率假設,公司估值的準確性會大大降低,最終影響到公司經營決策和長期發展。因此,壽險公司在估值時需要充分考慮未來死亡率可能存在的變動。
五、結論
本文考察了死亡率風險對壽險公司價值評估可能產生的影響,在壽險公司的估值和對應的風險管理方面給出了全新視角。本文借助CBD模型和內含價值評估方法模擬了在給定死亡率和預測死亡率下壽險公司價值的分布,從而分析未來死亡率的改善對公司價值帶來的影響。本文的產品模型在償二代框架下搭建,對壽險公司來說更具有借鑒意義。
研究結果表明:(1)無論是在現有生命表還是預測生命表的假設下,在年金產品同時包含生存給付和死亡給付時,其自身的對沖作用使得新業務價值受死亡率影響的幅度顯著小于壽險產品。(2)死亡率的改善會提高壽險產品的新業務價值,但年金產品自身的對沖作用使得新業務價值受影響的方向并不確定。如果兩種產品受影響的方向相反,則可以考慮通過自然對沖的方式穩定公司價值。(3)死亡率的改善會顯著影響壽險公司估值,如果估值過程中沒有充分考慮未來死亡率改善的因素,則可能導致公司估值和實際價值產生較大偏差,影響公司長期發展。因此,壽險公司在估值的過程中需要充分考慮到未來死亡率變動的因素。
本文首次將死亡率風險和公司估值因素聯系到一起,對壽險公司估值過程中的風險管理有一定指導意義,當然也存在不足。未來的改進方向可能有以下幾點:(1)本文假設死亡率風險是壽險公司面臨的全部風險來源,因此未來可參考壽險公司實際估值過程,將信用風險、市場風險等償二代下同樣關注的風險因素也納入考量范圍,使文章更具有現實意義;(2)本文對壽險和年金產品使用了相同的預測生命表,未來可將逆選擇效應納入考量,對兩種產品分別擬合出不同的預測生命表,以反映兩種產品保單持有人不同的潛在死亡風險;(3)本文側重于死亡率風險對公司價值產生的影響,未來可在此基礎上進一步考慮自然對沖等死亡率風險管理手段,對壽險公司準確估值提供更大的參考價值。

