探索和理解簡單組合的內涵

文|藍海鵬

讓學生更好地探索和理解簡單組合的內涵，可以采用如下教學過程。

一、情境理解，感受組合的原理

出示題目1：有一個勞動任務，需要2 人參加，自愿為主。小蘭、小芳和小華3 位同學自愿參加勞動，有哪些組合的方法？

1.獨立完成：學生閱讀后獨立思考，把自己的想法表示出來。

2.交流反饋：小組討論后，全班交流，引導學生發現：共有三種情況。“小蘭與小芳”和“小芳與小蘭”組合是一樣的。

二、多元表征，探索組合的規律

出示題目2：三張數字卡上的數字分別是5、7、9，任意選取其中2 個數字求和，得數有幾種情況？

1.想一想：想一想這樣的問題該如何解決，再動筆算一算。

2.擺一擺：你能用擺一擺的方法把你的思考過程表示出來嗎？學生嘗試，教師巡視并收集典型作品。

3.說一說：觀察圖1 和圖2，說一說，你看懂這個作品了嗎？是怎樣思考的？寫出算式求和，你有什么發現？討論后引導學生發現：“5 與7 的和”“7 與5的和”的結果都是12。圖2 更加簡潔。

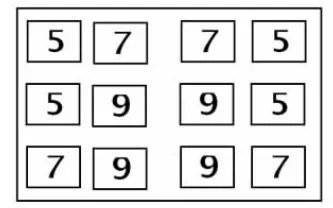
圖1

圖2

4.議一議：觀察圖3 和圖4，同桌議一議，看懂了嗎？你能說出他們是怎樣組合的嗎？

圖3

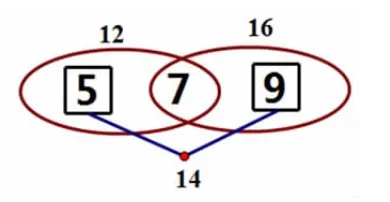
圖4

學生討論后發現，第1 個數分別與第2 個、第3 個數組合，第2 個和第3個數再組合。圖3 和圖4 的組合規律是一樣的。

5.理一理。

第1 個數第2 個數 求和 得數和有幾種情況575+7=12 12 75 59 95 79 97

學生整理表格數據后思考：你發現了什么規律？怎樣才能既不重復、不遺漏，又能讓思考變得有序、優化？

三、對比分析，揭示組合的本質

出示題目3：三張數字卡上的數字分別是5、7、9，用它們組成兩位數，每個兩位數的十位數和個位數不能一樣，能組成幾個兩位數？

1.嘗試解決，學生先試一試，完成后匯報、交流，教師有序板書。

2.分析交流：5 和7 這兩個數，組成兩位數有幾種情況？

3.對比聚焦：把題2 和題3 放在一起，觀察這兩道題，你發現了什么？它們有哪些相同點和不同點？點明：排列與數字順序有關，而組合則與數字順序無關。

在這樣的學習過程中，學生經歷嘗試、猜想、對比、發現等探索數學新知的活動，不僅有助于學生深入理解組合的本質，更能提高學生多元表征、有序表述、推理的能力，促進“四基”發展。