利用矢量的合成與分解巧解題

趙連森

（濱州實驗中學，山東 濱州 256600）

矢量的合成與分解是高中物理的一個重要知識點，平行四邊形定則是矢量的運算法則.高中物理課本先從位移、速度、加速度開始認識矢量，到力的合成與分解開始掌握矢量的運算方法，再到運用矢量的知識來解決運動的合成與分解問題，然后是沖量、動量以及電場強度和磁感應強度，這樣逐漸把矢量的知識延展開來.可是學生在解決問題時往往不能靈活合理的使用平行四邊形定則，造成解題時要么無從下手，要么繁瑣冗長，總是不得其要.下面我們通過幾個合理使用矢量合成與分解的實例感受一下.

例1.一勻強電場的方向平行于xoy平面，平面內a、b、c三點的位置如圖1所示，三點的電勢分別為10 V、17 V、26 V.下列說法正確的是

圖1

（A）電場強度的大小為2.5 V／cm.

（B）坐標原點處的電勢為1 V.

（C）電子在a點的電勢能比在b點的低7 eV.

（D）電子從b點運動到c點，電場力做功為9 eV.

此題的正確答案是（A）、（B）、（D），關于（A）選項電場強度大小的求解，通常的解法是這樣的：

因為a、b、c3點的電勢分別是10 V、17 V、26 V，如圖2所示，在ac連線上，確定一b點，電勢為17 V，則bb′連線，即為等勢線，那么垂直于bb′的連線ce，則為電場線，再依據沿著電場線方向，電勢降低，則電場線方向如圖2所示.

圖2

因電場為勻強電場，則有

則b′點的坐標為（3.5 cm，6 cm）

依據幾何關系，則

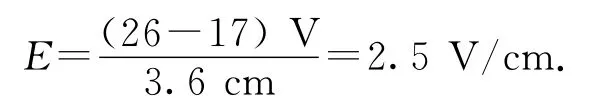
這種方法求解電場強度是最常用的方法，先確定等勢面，再利用電場線與等勢面垂直確定電場線的方向，最后利用電勢差和沿電場線方向上的距離求解電場強度.在上面解法中，利用數學關系較多，解題過程冗長復雜.而如果依據電場強度的矢量性，先求出電場強度在x、y方向上的分矢量Ex、Ey，再合成就簡單多了.

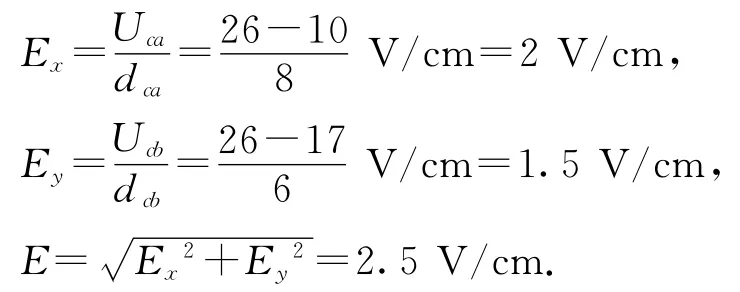
根據以上解題過程不難看出，此解法簡單易懂，利用了電場強度的矢量性，先求出電場強度在x、y方向上的分矢量，再利用分矢量合成求解出合矢量.在高中物理中，除了電場強度，在解決運動的合成與分解時，把位移、速度、加速度三個矢量進行分解解題的例子也有很多.

例2.（2020年山東高考16題）單板滑雪U型池比賽是冬奧會比賽項目，其場地可以簡化為如圖3所示的模型：U形滑道由兩個半徑相同的四分之一圓柱面軌道和一個中央的平面直軌道連接而成，軌道傾角為17.2°.某次練習過程中，運動員以vM=10 m／s的速度從軌道邊緣上的M點沿軌道的豎直切面ABCD滑出軌道，速度方向與軌道邊緣線AD的夾角α=72.8°，騰空后沿軌道邊緣的N點進入軌道.圖4為騰空過程左視圖.該運動員可視為質點，不計空氣阻力，取重力加速度的大小g=10 m／s2，sin72.8°=0.96，cos72.8°=0.30.求：

圖3

圖4

（1）運動員騰空過程中離開AD距離的最大值d；

（2）M、N之間的距離L.

此題用運動的合成與分解解題是最快捷的，把速度和加速度分別沿垂直于AD和平行于AD方向進行分解，然后沿各自方向計算位移即可.解法如下.

對于此題中這種較復雜的曲線運動，要解題還是要根據運動的矢量性，把復雜的曲線運動分解成兩個直線運動，再利用它們的位移、速度、加速度關系進行求解.

上例的特點是可以清晰的看出物體做曲線運動的軌跡，我們把曲線運動分解成兩個直線運動，再根據各分運動的性質來求解即可.還有的問題是沒有給出物體的運動軌跡，僅是已知分運動的運動情況，讓我們根據位移、速度、加速度的矢量性來解決問題.

例3.（2013年全國Ⅰ卷24題）如圖5所示，水平桌面上有兩個玩具車A和B，兩者用一輕質細橡皮筋相連，在橡皮筋上有一紅色標記R.在初始時橡皮筋處于拉直狀態，A、B和K分別位于直角坐標系中的（0，2L）、（0，-L）和（0，0）點.已知A從靜止開始沿y軸正向做加速度大小為a的勻加速運動.B平行于x軸朝x軸正向勻速運動.在兩車此后運動的過程中，標記K在某時刻通過點（L，L）.假定橡皮筋的伸長是均勻的，求B運動速度的大小.

圖5

此題沒有給出標記K具體的運動軌跡，但根據運動關聯性，能夠知道其在x、y方向上的分運動情況：x方向上勻速直線運動，y方向上勻加速直線運動.知道了分運動情況，沿x、y分方向處理就可以了.

通過以上幾例可以看出，根據矢量運算的特點，利用好矢量的分解與合成解題，很多情況是簡單易懂的.回顧高中學習的物理量，最常用的矢量主要是位移、速度（動量）、加速度、力（沖量）、電場強度和磁感應強度，在學習過程中多注意這幾個矢量的合成與分解就可以了.