大概念視角下的單元教學設計實踐與價值

胡曉敏

[摘 要]以大概念為視角的單元教學設計是當前國際教學研究發展的新趨勢，大概念的內涵強調知識的理解、聯結和遷移，為小學數學課程落實學科核心素養帶來新的契機和可能。在研究實踐中，基于大概念的單元教學設計的價值研究，可促進學生對知識本質的理解，助力學生對知識結構的聯結和推動知識思維的遷移。

[關鍵詞]大概念;單元教學;設計

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）29-0023-03

2018年初，教育部發布了《普通高中數學課程標準（2017年版）》，其中凝練了數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析六個學科核心素養，并明確強調以學科大概念統整課程內容，并以此為核心促進數學核心素養的落實。2019年初，崔允漷教授在“學科核心素養呼喚大單元教學設計”中提出，單純知識和技能的掌握不能直接轉化為學生的價值觀念、必備品格和關鍵能力。學科核心素養的出臺倒逼教學設計的變革，因此，小學數學教學設計也應順應趨勢，從設計一個知識點或課時，轉變為設計一個大單元。

由此可見，以大概念視角下的單元教學設計探索在教學中落實學科核心素養，具有較高的現實意義。基于一些思考和實踐，筆者以人教版小學數學教材為例，與大家分享大概念在小學數學單元教學設計的實踐與價值。

一、大概念的內涵與理解

大概念（Big Ideas），也有學者將其譯為大觀念。事實上，有關大概念的研究至少可以追溯到布魯納對于教育過程的研究。埃里克森（H.Lynn Erickson）認為大概念是學科的核心概念，是基于事實基礎上抽象出來的深層次的、可遷移的概念。威金斯和麥克泰格（Wiggins & McTighe）在《追求理解的教學設計》中提出，大概念是處于課程學習中心位置的觀念、主題、辯論、悖論、問題、理論或者是原則等，能夠將多種知識有意義地聯結起來，是不同環境中應用這些知識的關鍵。查爾斯（Charles.R.I）將數學大概念定義為對數學學習至關重要的觀念，是數學學習的核心，能夠把各種數學理解聯系成一個連貫的整體，大概念使我們將數學知識看作是一個連貫的集合。

結合上述專家的研究和小學數學的特點，筆者認為大概念在數學教學中具有3個內涵特征。首先，大概念不是單個基礎概念，而是有兩個或兩個以上基礎概念聚合的，相對于一般概念而言的，更具抽象水平，更具有一般意義的概括性表達。其次，大概念可以是同一個年級幾個單元的大概念，也可以縱跨不同年級，甚至橫跨多個學習領域的概念，使散狀的知識點呈現一定的網狀結構，起到提綱挈領的重要作用。最后，大概念是一個“長時記憶”的內容或結構，是在經驗和事實消失之后還留存的核心概念，也是一般觀念，這個一般觀念可以幫助學生認識后續的問題，即遷移到新知識、新情境或新領域，甚至不同的學科。

二、大概念在單元教學設計中的實踐與價值

當下的課程教學需要重新思考“把人作為一個完整的人”來培養，要學習“像專家一樣思考”，教學設計要從知識點走向單元，提高站位和格局。依據某一大概念進行思考，關注知識的本質、邏輯、關系和價值等各個方面，為重新確立和組織單元教學設計提供有效路徑。

1.促進知識本質的理解

教學中，學生最應該得到的是對于知識策略的本質性理解，也就是知識背后的知識，也即觀念。大概念是學科的中心概念，最能代表學科本質和基本結構。

“圖形的運動”是小學數學的重要內容，人教版分別安排在四、五年級，順序依次為軸對稱圖形、平移、旋轉。部分教師以“課時”和“知能”為視角，往往會忽視各個知識點之間的關系，并把“能在方格紙上畫出簡單圖形運動后的圖形”作為教學重點。

基于大概念的單元教學設計，引導教師去思考軸對稱圖形、平移和旋轉分別是什么樣的運動？這三種運動有什么關系？學習它們有什么意義？不難發現，平移、旋轉和軸對稱圖形（翻轉）是平面圖形的三種基本運動形式，它們共同的特點在于能夠保持圖形大小和形狀不變，這種圖形運動也叫圖形的剛體運動，即剛體運動所發生的變化是全等變換。因此，“圖形的運動”單元的大概念就是“在變換過程中發現不變的規律或性質”，這也是探究自然和社會發展規律的一個基本思維。1872年，聞名遐邇的德國數學家F·克萊因把幾何學看作是研究各種變換群之下的不變量的一門學問，對幾何思想的發展產生了深遠的影響。

再進一步，教師便可基于“在變換過程中發現不變的元素和變化的規律”，對第二學段的“圖形的運動”內容進行大單元的設計或重構，即先學平移和旋轉、再學軸對稱圖形，并以“運動中，什么變了？什么沒有變？”為基本問題，引導學生學習探究。其實，在平移和旋轉的過程中，圖形上的每一個點都是沿相同方向移動了相同的距離（角度）。軸對稱圖形相對比前兩者復雜，是三維空間的翻轉運動，但其實質也是沿相同方向移動了相同的角度。教學過程中，學生運用“在變換過程中發現不變的元素和變化的規律”大概念，不僅能較快地發現運動后圖形大小、形狀沒有變的本質，而且能準確理解圖形變換的規律。學習后，學生不再認為學習“圖形的運動”僅僅是畫圖，而是對軸對稱圖形、平移、旋轉的描述也更加具體和豐富，厘清了三者之間的聯系與區別。顯然，基于大概念的單元教學設計，促進了學生對知識本質的理解。

2.助力知識結構的聯結

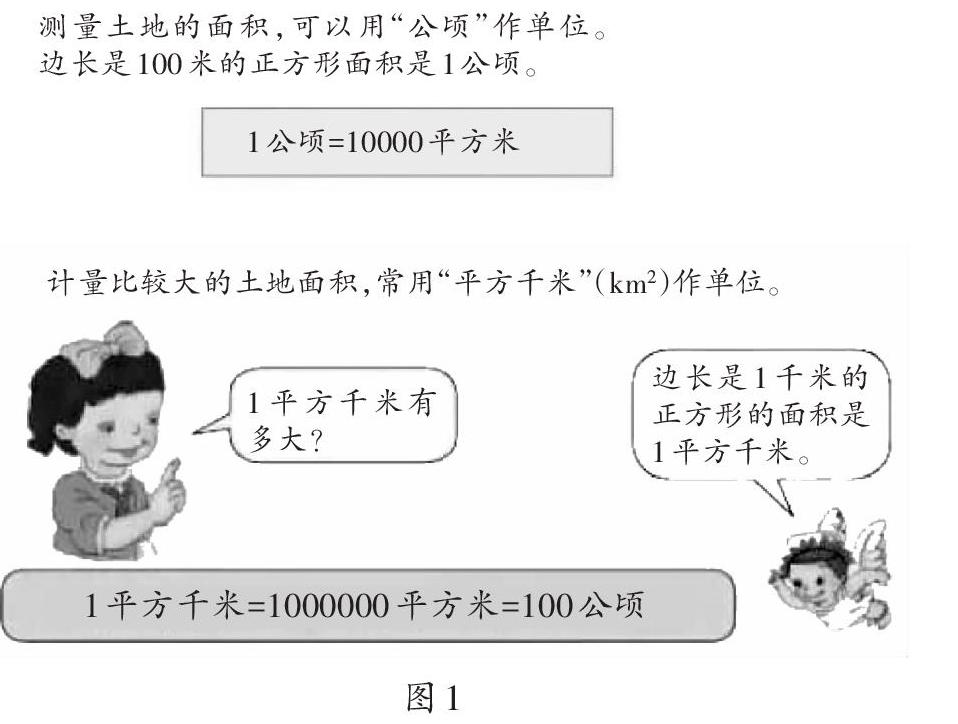
數學是“結構”的科學，布魯納（J.S.Bruner）認為，數學還是一門研究“關系”的學科，這也是單元教學設計的追求所在。但是，因為某些客觀原因，教材往往選擇那些重要的、常用的知識和技能編排呈現，且分別安排在不同年級。如，四年級上冊的“公頃和平方千米”是在第一學段學習平方厘米、平方分米和平方米基礎上進行的，教材用方框呈現了“知能”的重點（如圖1），即1公頃=10000平方米，1平方千米=1000000平方米=100公頃。

如果教師照本宣科，學生只能死記硬背公式，導致混淆不同單位之間的進率，甚至直至小學畢業，學生還存有“為何面積單位的進率要變來變去”的疑惑。然而，利用好“相鄰單位進率都是一致的”大概念進行單元教學設計，讓長度單位之間、面積單位之間形成等比的“階梯”結構（如圖2），就能更好地突破知識的瑣碎、零散問題，促進知識橫向聯結的發生，形成知識之間的聯結通路。具體教學中，教師可以在學生自主整理三個已學的面積單位的基礎上，依據建立“相鄰單位進率都是一致的”大概念，通過“創造更大的第四、第五、第六個面積單位”這個任務展開學習討論，從而發現平方十米（公畝，非教材編排內容）、平方百米（公頃）、平方千米的單位，完善“相鄰面積單位進率都是100”的認知結構，體驗到數學的整體性、邏輯性和嚴密性。

類似地，在質量、體積等單元課程的教學設計中，也可以引用“相鄰單位進率都是一致的”大概念。這樣做，不僅可以讓相同計量單位之間產生緊密關系，甚至可以讓不同的計量單位也產生了某種“美妙”的聯結，非常好地體現了皮亞杰（J.Piaget）的觀點，他認為全部數學都可以按照結構的建構來考慮，而這種建構始終是完全開放的……這種結構或者正在形成“更強的”結構，或者在由“更強的”結構來予以結構化。

3.利于知識遷移的發生

A.普雷斯利和同事開展的關于策略教學研究表明：學習一般策略或原理，有助于解決多種不同的任務。大概念也相類似，它不是抽象概念或另一個事實，而是概念性工具，用于強化思維，連接不同的知識片段。

例如，教學五年級“因數和倍數”時，如果教師完全割裂知識之間的聯系，以課時進行教學，那么學生就會誤認為“2、5”的倍數特征的學習與后續“3、9”“4、8、25”等的倍數特征的探究沒有什么關系。若以“判斷某數的倍數與其每一數位上的數字緊密相關”的大概念開展單元設計和整體教學，就會讓知識之間產生關系，先學的“2、5”的倍數特征對后續的新知識、新探究就會產生積極的影響。具體地說，“2、5”的倍數特征與每一數位上的數字緊密相關，如264可看成200+60+4，200、60都已經是2和5的倍數，那么只要看個位4是不是它們的倍數即可。有了“判斷某數的倍數與其每一數位上的數字緊密相關”的大概念后，就能比較好地理解3和9的倍數特征為何是“各個數位上的數字之和也是它們的倍數”。如264可看成200+60+4，200除以3余2，60除以3沒有余數，4除以3余1，2+0+1=3，即264是3的倍數但不是9的倍數，因此就有了各個數位上的數字是否是3、9的倍數的判斷方法。進而，也為后續探究“4、8、25”的倍數特征積累數學活動經驗和思維基礎。

又如，教學五年級“可能性”時，教材中的游戲活動本質上都是古典試驗，所有的可能性大小就是基本數據的多與少。因此，教師就可以用“每個基本結果的可能性都一樣時，平分游戲結果就可以保證公平”的大概念整體設計開展教學。

綜上所述，大概念在單元教學設計中的實踐探索為落實數學核心素養提供了一種思路，但在具體應用中還需要處理諸多事項。首先，大概念本身不是一個確切的答案或事實，在小學數學教學中的內涵還需進一步思考和明確，以便被更多教師理解和接受，進而推進大概念視角下的單元教學設計的實踐。其次，目前的具體實踐還是以人教版教材中的單元為基礎，大概念的提取可能還不夠開放和“大”，也不否認單元或大單元設計方式的多樣化及其他路徑。最后，本文著重談了大概念視角下單元設計的價值，而如何提煉大概念、運用大概念教學等方面還需更深入的思考和探索。

[ 參 考 文 獻 ]

[1] 中華人民共和國教育部.普通高中數學課程標準（2017年版）[S].北京：人民教育出版社，2018.

[2] 中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2012.

[3] Grant Wiggins，Jay McTighe.追求理解的教學設計[M].閆寒冰，宋雪蓮，賴平 譯.上海：華東師范大學出版社，2017.

[4] 李剛，呂立杰.國外圍繞大概念進行課程設計模式探析及其啟示[J].比較教育研究，2018，40（9）.

[5] 邵朝友，韓文杰，張雨強.試論以大觀念為中心的單元設計——基于兩種單元設計思路的考察[J].全球教育展望，2019，48（6）.

[6] 張奠宙，孔凡哲，黃建弘，等.小學數學研究[M].北京：高等教育出版社，2009.

[7] 崔允漷.學科核心素養呼喚大單元教學設計[J].上海教育科研，2019（4）.

[8] 許衛兵.結構化學習：回歸“本原”的課堂實踐[J].小學數學教師，2018（Z1）.

（責編 李琪琦）