大道至簡

李志鴻

[摘 要]數學有很多定理和公式，它們內涵豐富、道理深奧，有時教師講解得天花亂墜，還比不上讓學生動手操作一次。不過，這操作是有講究的，需要教師精心設計。

[關鍵詞]線段;三角形;邊長;兩邊之和;操作

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）29-0028-02

一次，筆者要上一節公開課。為了與教學進度同步，筆者選擇了正要上的新課——蘇教版教材第八冊第三章“三角形”?；叵肫鹨酝虒W“三角形”，筆者用課件呈現由紅、綠、紫三種顏色的小棒圍成的三角形，從“紅+紫>綠”、“紅+綠>紫”到“綠+紫>紅”，說得口干舌燥之后，學生終于開竅了，他們在筆者的提示下，連蒙帶猜地說出“兩邊的長度之和大于第三邊”的結論。五彩斑斕的課件、連篇累牘的板書、頻繁的你問我答……于是，筆者下定決心，換一種面貌走進課堂。

一、刪繁就簡，直擊要害

【教學預案】

1.課前預習

（1）課前動手制作一個三角形框架。觀察、觸摸三角形框架，說一說你制作的三角形框架一共有幾條邊、幾個角、幾個頂點。

（2）“三角形兩邊長度的和大于第三邊”這個結論到底正不正確？請聯系課本上的例子進行思考，可以使用學具袋里的木棒試著拼擺一下，也可以在小組內探討商議。

（3）關于三角形，你還了解到什么重要信息？有沒有什么疑惑？

2.課中研習

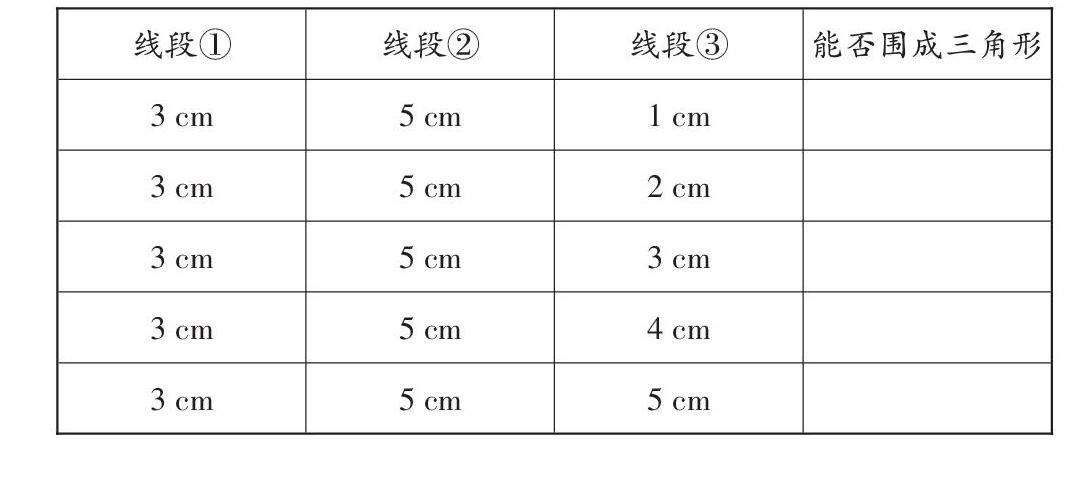
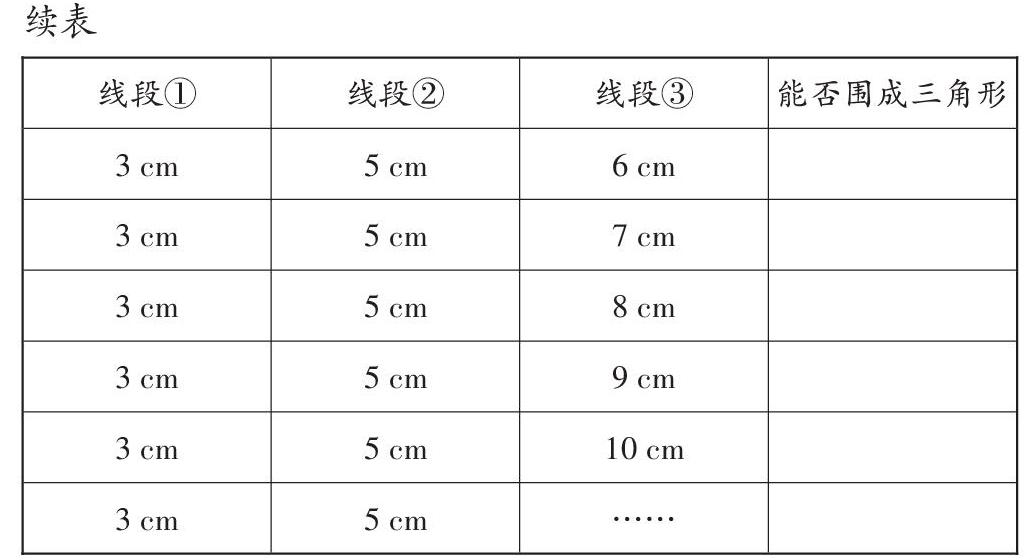
（1）幾厘米長的線段可以與下面兩條線段圍成一個三角形？（取整厘米數）

（3）有兩條線段，分別長2 cm、7 cm，想一想，幾厘米長的線段能和它們圍成三角形？（取整厘米數）

3.課后練習

（1）測得已知線段長6 cm，探尋另外兩條合適的線段，使它們能與已知線段圍成三角形。（取整厘米數）

（2）怎樣的四條線段才能圍成四邊形？（探究四邊形四條邊的長度關系）

從預習反饋的效果來看，學生對三角形有“三個角、三個頂點、三條邊”已經爛熟于心，因此筆者認為在認識三角形這個環節中無須多費時間，直接請學生匯報就行。本課研習的重頭戲是對“三角形任意兩邊長度的和大于第三邊”這個定理的驗證和理解。

課本中的例題給出了四根長度不一的小棒，讓學生在甄選、拼擺的同時記錄小棒的長度組合以及能否圍成三角形。在以往的課堂中筆者對學生進行詢問，他們一致認為操作的目的是“驗證能否圍成三角形”。從學生進行操作時的毛手毛腳，以及得出結論的含含糊糊可以看出，學生的操作是無意識的，認識是淺薄的。鑒于此，這次筆者在處理這一環節時，舍棄了課本例題，直接提供兩條長度分別為3 cm和5 cm的線段，讓學生猜想幾厘米長的線段可以與它們圍成一個三角形。

對于這些操作，筆者預期的目標有兩個。1.檢查預習效果。由于課前預習時有些學生不屑于操作，而是實行“拿來主義”，直接利用課本中現成的結論“三角形任意兩邊長度的和大于第三邊”去挑選小棒。而通過筆者這樣處理，就可以真實反映出學生對“三角形任意兩邊長度的和大于第三邊”這個結論的理解程度。2.檢驗、體驗。選好小棒之后，學生開始操作。學生通過實踐檢驗選擇的小棒是否符合條件，在操作中深切體會到“當兩邊長度的和大于第三邊時，三條線段首尾相連圍成了一個三角形”。治學之道在于務實，教師去除花哨的“裝飾”，留足時間讓學生充分操作、體驗，就能促進學生在自主活動中追根溯源。

二、蜻蜓點水，畫龍點睛

交流環節，筆者意圖通過師生、生生之間的交流與溝通，讓學生的操作經驗得以提升。縱觀整個交流環節，筆者一共點撥了兩次。

【第一次點撥】

下面這種情況同樣滿足“兩邊長度的和大于第三邊”的條件，但圍不成三角形，為什么剛才那個定理不適用了？多長才可以圍成？多長就圍不成？（PPT出示長8 cm的線段，如下圖所示）我們一起看看8 cm長的線段能不能滿足條件。原定兩條線段的長度的和剛好為8 cm，會發生什么情況？

用這三條線段始終無法圍成三角形。如果把8 cm長的線段延長，比如延長為8.5 cm，可以圍成嗎？此時，又有什么情況發生？ 3 cm、5 cm長的兩條線段的端點分離了，出現了一個斷口（如下圖）。

把8 cm長的線段換成9 cm、10 cm長的線段可以圍成嗎？換成其他長度的線段，還會不會出現兩邊長度的和等于第三邊的情況？（2 cm，如下圖）

比2 cm短的線段能圍成嗎？

經過討論可以發現，長度為3～7 cm的線段是符合條件的，超出這個范圍的就不符合。也就是說，任意兩邊長度的和要大于第三邊才能圍成三角形。上述例子中，3+5=8，不滿足“任意”這一要求，故而不符合條件。一定要謹記，是任意兩邊長度的和大于第三邊。

給出長度一定的兩邊，讓學生嘗試確定第三邊的長度，這種操作具有一定的局限性，容易讓學生形成思維定式：學生會死板地將事先給定的兩邊看作“兩條邊長度的和”中的兩條邊，長度待定的那條邊看作第三邊。這樣一來，他們就會固執地將長度已知的兩條邊求和，然后以此為標準去尋找第三邊。比如上述例子中，學生將3 cm和5 cm長的兩條線段死死捆綁在一起，只是不斷變換第三條線段的長度，加上操作上固執地讓已知兩邊形成夾角（忽略重疊的情況），由此得出片面的結論：3 cm+5 cm>第三邊的長度，從而推出第三邊的長度<8 cm。筆者用“還會不會出現兩邊長度的和等于第三邊的情況？”這一問題引出第二步操作，有效彌補了漏洞，在操作上已定的兩邊既可以連接共線，也可以重疊共線，在理論上也就是將給定的5 cm線段作為第三邊（設活動邊的長度為a cm），那么就有a+3>5，因此a>2。同理，可以將3 cm長的線段視為第三邊，就有a+5>3，此時a可以是任意自然數。綜合考慮，a的取值范圍為2

【第二次點撥】

誰能用一個算式來概括？再來嘗試一題。有長2 cm、7 cm的兩條線段，多長的線段可以和它們圍成三角形？（長6 cm、7 cm、8 cm的線段能，長5 cm、9 cm的線段不能）你的判斷依據是什么？（學生老老實實寫出三個算式：[a]+2>7，[a]+7>2，7+2>[a]）誰能將以上三個算式濃縮為一個算式，使得根據這個算式可以立馬判斷三條線段是否能圍成三角形？

任意兩邊長度的和大于第三邊，列成算式也就是7-2<[a]<7+2。這個算式囊括了所有情形，因此這種判斷法更為簡捷。

三、課后總結與反思

每一節數學課都有自己的重難點，它們可能指向數學概念內涵，也可能指向數量關系，還可能指向基本方法應用，或指向某種數學思想……教師要針對這些重難點制訂相應的教學策略。不管是在預習時，還是在課堂交流過程中，教師都不能袖手旁觀，而要適時干預，引領學生展開討論;適度點化，提供交流平臺，提升交流效果;適時鼓勵，引導學生深入思考。教師之導，看似輕描淡寫，實則是點睛之筆。

傳統的課堂是把探究“多長的線段能和3 cm、5 cm長的線段圍成一個三角形”這一環節安排在課的末尾，作為課后提升、延伸的內容。而筆者反其道而行之，將其作為開頭環節，棄用課件，板書簡練，讓學生在操作中體驗、在交流中思辨，大道至簡、樸素無華。這種做法是化繁為簡，以最小的時間成本換取最豐富的情感體驗，以最直接的方式獲取最大的知識收益，以最接近學生的起點帶領他們展翅高飛。

（責編 吳美玲）