分布式電驅動車輛極限越野環境下高速避障與穩定性控制

劉聰， 劉輝,2， 韓立金,2， 陳科

(1.北京理工大學 機械與車輛學院, 北京 100081; 2.北京理工大學 前沿技術研究院, 山東 濟南 250300;3.內蒙古第一機械集團股份有限公司， 內蒙古 包頭 014032)

0 引言

相比搭載發動機的機械傳動車輛，分布式電驅動車輛具有各輪驅動力矩獨立可控、驅動電機響應迅速以及轉速、轉矩可精確測量等優勢，特別是在車輛底盤動力學控制方面，具有很大的發展潛能[1]。分布式電驅動車輛憑借其高機動性以及高冗余性的優勢，可高速且靈活躲避障礙物，具有快速突擊能力和操縱穩定性能，廣泛應用于民用和軍事領域[2]。

為推進分布式電驅動車輛的快速發展，許多學者針對提高其操縱穩定性和機動性兩方面進行了相關研究[3-4]。Jin等[5]提出一種基于線性變參數技術的分布式驅動電動汽車橫向穩定性魯棒增益調度控制器，具有高效的跟蹤性能和對不確定性的較強魯棒性。為提高車輛在極限工況下的橫向穩定性， Chen等[6]提出一種基于2階滑模控制和非線性干擾觀測器相結合的自主4輪獨立驅動電動汽車路徑跟蹤和穩定性控制方法，對不確定性干擾具有良好的魯棒性。Li等[7]提出一種極限工況下基于模型預測控制理論的車輛縱向、橫向協調穩定性控制器方法，解決輪胎力在高度非線性情況下車輛橫向、縱向運動的耦合問題。為提高分布式驅動車輛低速轉向機動性和高速行駛穩定性，胡金芳等[8]提出一種適應車速變化的4輪轉矩分配策略。此外，劉聰等[9]提出一種基于轉向狀態預測的穩定性分層控制策略，可避免車輛在緊急避障過程中因時間延遲或是駕駛員反應不及時而引起的車輛失穩。祁炳楠等[10]提出一種基于能量法的分布式驅動電動車輛防側翻穩定性控制策略，通過主動分配兩側驅動力矩來有效抑制整車側傾運動。王偉達等[11]提出一種基于非線性聯合滑模變結構的4輪獨立驅動電動車橫向穩定性控制策略，其可提高極限工況下車輛的操縱穩定性。謝偉東等[12]提出一種基于最優轉矩矢量控制的分布式驅動車輛側向穩定性控制系統。針對雙側獨立電驅動履帶車輛的行駛穩定性問題，張杰等[13]提出一種解耦和預測控制方法，可對縱向車速和橫擺角速度進行解耦及獨立控制。李勝琴等[14]提出一種基于滑模控制理論及罰函數法的分布式驅動電動汽車橫擺穩定性控制策略。Zhou等[15]提出一種基于非線性模型預測控制(NMPC)的橫向、縱向協調控制方法。Peng等[16]為實現4輪自主電機獨立驅動電動汽車的協調路徑跟蹤和直接橫擺力矩控制，提出一種具有有限時域的魯棒模型預測控制(MPC)。然而，當前研究成果僅基于單一且傳統的2自由度車輛動力學模型來設計分布式電驅動車輛的橫擺力矩控制器，極限失穩情況下車身姿態修正無法達到精確控制，不能充分發揮4輪獨立可控的獨特優勢。因此，構建一種適用于分布式電驅動車輛的橫擺運動動力學方程是必要的。

本文針對分布式電驅動越野車極限環境避障過程中的路徑保持和橫向穩定性方面進行研究。為解決車輛在大幅度側滑、甩尾等失穩情況下很難依靠質心橫擺力矩控制來即時修正車身姿態的問題，提出一種協同考慮質心處和后軸中心處車輛狀態信息的避障橫向穩定性控制方法，細化了分布式電驅動車輛的橫擺運動模型，構建一種新穎的雙層融合型橫擺運動車輛動力學方程。綜合考慮越野環境中車輛系統非線性、時變性以及控制約束等性能指標，提出一種基于數據驅動多模型測控制的橫擺、側傾穩定性分層協調控制方法。

1 分層協調橫向穩定性控制器結構

本文所提出的分布式電驅動車輛分層協調橫向穩定性控制器結構圖如圖1所示，整個控制系統分為上、下兩層結構，上層控制器為橫擺、側傾力矩集成控制，下層為4輪驅動轉矩協調控制。圖1中，Mz為融合型橫擺力矩，δf為前輪轉角，T1、T2、T3、T4分別為下層控制器預分配的左前電機轉矩值、右前電機轉矩值、左后電機轉矩值、右后電機轉矩值。

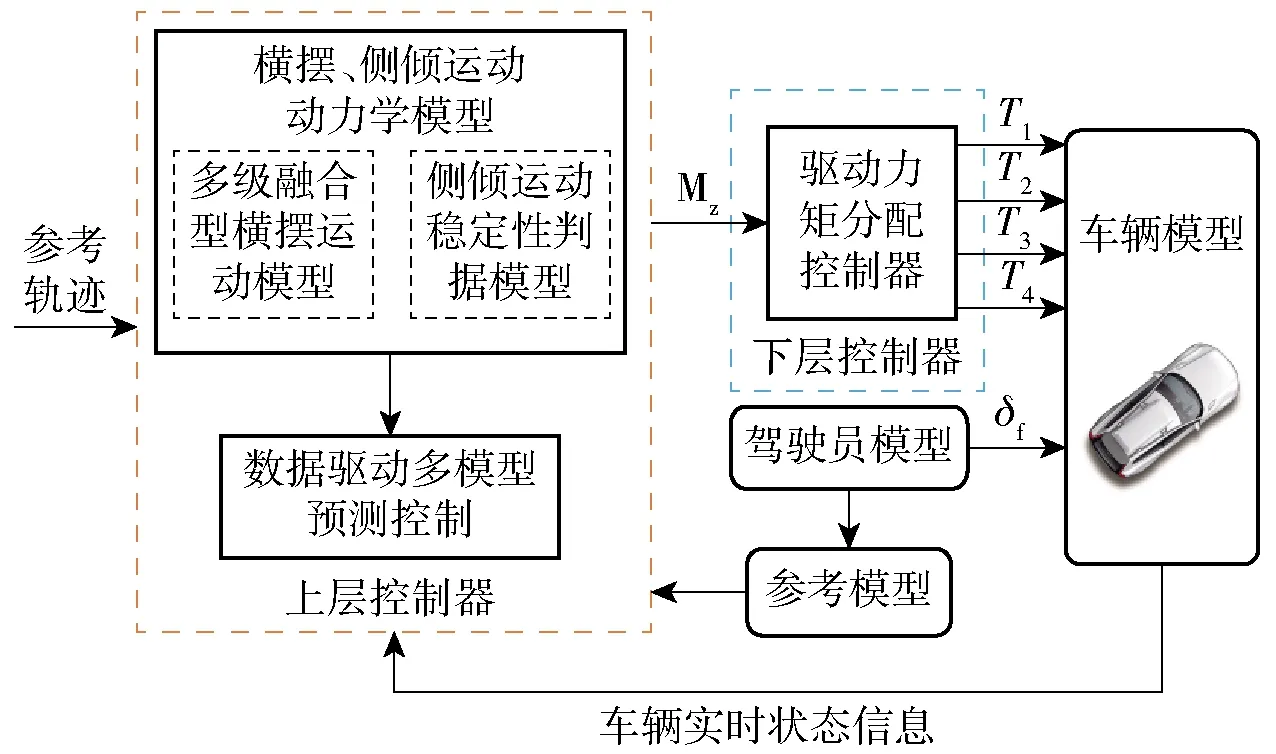
圖1 分層協調穩定性控制器框架Fig.1 Hierarchical coordinated stability controller framework

2 車輛動力學模型構建

2.1 傳統橫擺運動動力學模型

本文主要研究分布式電驅動車輛二維平面內的橫向動力學運動，僅需考慮縱向運動、側向運動、橫擺運動以及4個車輪轉動的7自由度車輛動力學模型，如圖2所示。圖2中，Oxyz為車體坐標系，L為軸距，a、b為分別為質心到前軸、后軸的軸距，β為質心側偏角，ωrc為車輛繞質心處的橫擺角速度，v為車輛質心速度，vx為車輛的縱向速度，vy為車輛的側向速度，Fxi(i=1,2,3,4)為各車輪所受縱向力，Fyi為各車輪所受側向力，αf、αr分別為前輪胎、后輪胎側偏角。

圖2 7自由度模型Fig.2 7-DOF model

7自由度的運動微分方程如下。

縱向動力學方程為

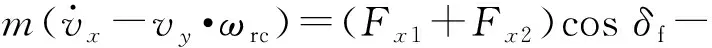
(1)

側向動力學方程為

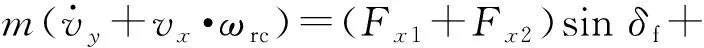
(2)

繞質心位置的橫擺運動方程為

(3)

車輪的轉動方程為

(4)

式中：m為整車質量；Iz為車輛繞z軸的轉動慣量；B為前軸、后軸輪距(本文假設二者相等)；Jw為車輪轉動慣量；ωi為車輪角速度；Ti為輪轂電機轉矩；r為車輪滾動半徑。

常規的橫擺運動控制方式為基于車輛質心位置的橫擺力矩控制，其可以保證車輛在小范圍內失穩情況下的橫向穩定性[17]。繞質心做橫擺運動的2自由度車輛動力學微分方程為

(5)

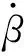
2.2 雙層融合型橫擺運動動力學模型

當車輛由于大幅度側滑甩尾而發生失穩時，后軸中心位置首先偏離期望軌跡。當偏離程度較為嚴重時，車輛最理想的橫擺運動中心位置出現漂移現象，逐漸向前軸中心位置逼近，傳統的僅考慮質心位置的橫擺力矩控制方式已無法滿足極限工況下的車身姿態修正需求。為解決以上問題，本文構建了一種雙層融合型橫擺運動動力學模型，其中所構建的繞前軸中心位置的橫擺運動方程為

(6)

式中：Izf為繞前軸中心的轉動慣量；ωrf為繞前軸中心的橫擺角速度。

考慮到繞前軸中心的橫擺運動，控制系統需要優先計算用于穩定后軸中心軌跡偏離程度的附加橫擺力矩Mzf，所構建的繞前軸中心的橫擺角速度微分方程為

(7)

式中：C3為左后輪的側偏剛度；C4為右后輪的側偏剛度。

通過以上分析，得到兩種控制模式下的雙層橫擺角速度方程組表達式為

(8)

式中：C1、C2分別為左前輪側偏剛度和右前輪側偏剛度。為提高車輛的路徑保持能力，需要保證車輛自身位置坐標實時維持在期望坐標附近。本文同時考慮了車輛質心位置和后軸中心位置偏離期望坐標點的程度，提高車輛橫擺力矩控制的時效性。

車輛質心坐標位置計算公式為

(9)

式中：Ψ為車輛的航向角。后軸中心坐標位置計算公式為

(10)

根據輪胎側偏特性，可得輪胎的縱向力表達式為

(11)

式中：Fxf、Fxr分別為前輪、后輪縱向力；Clf、Clr分別為前輪、后輪胎縱向剛度；sf、sr分別為前輪、后輪胎滑移率。

輪胎側向力表達式為

(12)

式中：Fyf、Fyr分別為前輪、后輪胎側向力。

輪胎滑動率s的表達式為

(13)

式中：ω為車輪轉速。

綜上所述，車輛在極限越野工況下進行避障時一般存在兩種橫向失穩的情況：一種失穩情況為小范圍側滑失穩，可通過基于質心處附加橫擺力矩控制保證車輛轉向穩定；另一種失穩情況為后車身大范圍甩尾側滑，輪胎力處于非線性工作區域，常規控制方式已無法即時修正車輛姿態。

本文針對分布式電驅動車輛4輪獨立可控的獨特優勢，提出一種新穎的雙層橫擺角速度表達式，融合質心處和前軸中心處的兩種橫擺運動模式，可基于當前車輛的失穩程度分時調整當前橫擺運動的最佳控制模式，從而實現4個驅動輪的驅動力矩即時且精確地修正當前車身失穩姿態，運動控制方式如圖3所示。

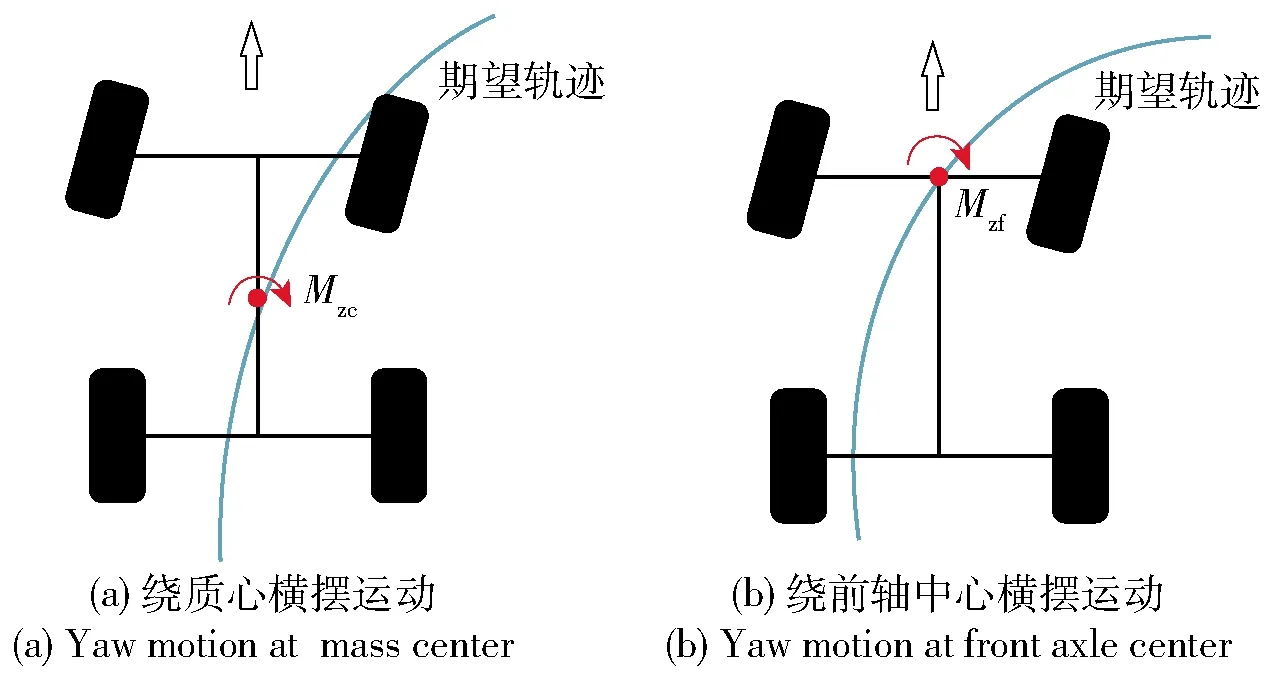
圖3 兩種橫擺運動控制模式Fig.3 Two yaw motion control modes

考慮到車身兩處橫擺力矩同時控制中存在耦合問題，并且增大控制器計算復雜度。為解決以上問題，本文分別將兩處的橫擺角速度觀測值和附加橫擺力矩控制量合理地融合在質心位置，如(14)式和(15)式所示。

融合型橫擺角速度表達式為

(14)

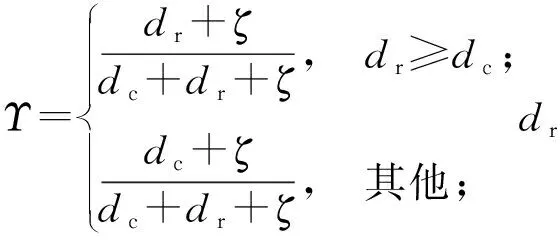
融合型橫擺力矩表達式為

(15)

2.3 橫擺、側傾協調運動動力學模型

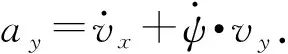
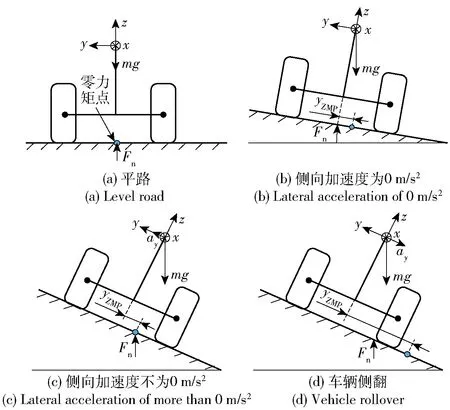
圖4 零力矩點分布Fig.4 Zero moment point distribution

基于零力矩點的側傾力矩平衡，可以得到

(16)

式中：φ為道路側傾角；h為質心高度；Ix為車輛繞x軸的轉動慣量。

對φ進行小角度假設，對(16)式進行近似線性化，可以得到零力矩點的橫向偏移量yZMP的表達式為

(17)

參考車輛輪距的一半距離，對零力矩點的橫向偏移量yZMP進行歸一化處理，得到

(18)

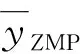
假設高速行駛的車輛前輪轉角較小，即cosδf≈1,sinδf≈δf，構建滿足以上需求的簡化車輛動力學模型，如(19)式所示：

(19)

基于以上公式，得到的分布式電驅動車輛離散化非線性動力學方程為

y(k)=f(X(k),u(k)+ε(k))，

(20)

式中：y(k)為輸出量，y=[β,ωr,ψ,yZMP,y,yr]T，k為時間序列；X為狀態量，X=[β,ωrc,ωrf,ωr,vx,vy,ψ,yZMP,x,y,xr,yr]T；u(k)為控制量，u=[Mzc,Mzf]T；ε(k)為零均值白噪聲。

3 橫擺力矩控制器設計

NMPC具有解決多輸入、多輸出非線性系統的在線約束能力，通過狀態預測，滾動優化和反饋求解可得到系統的實時最優控制量。但是，由于車輛實際行駛工況復雜、多變，當車輛系統出現大范圍參數變化或是行駛狀態突變時，NMPC缺乏針對環境的自適應能力。

本文提出一種基于數據驅動多模型預測控制的橫擺力矩控制方法，將車輛局部多模型在線建模與控制預測量相結合，根據系統輸入/輸出數據庫確定其當前工作點，在線構建系統的局部多模型。該控制系統結構框圖如圖5所示。圖5中：y(k+λ+1|k)表示k為起始時刻，預測模型在k+λ+1時刻的輸出量，λ為時刻；yr(k+1)為k+1時刻的期望輸出量，r(k+λ+1|k)表示k為起始時刻，k+λ+1時刻的期望控制量；u(k+λ|k)為表示k為起始時刻，k+λ時刻的實際控制量；Δu(k+λ|k)表示k為起始時刻，k+λ時刻實際控制量的變化量。

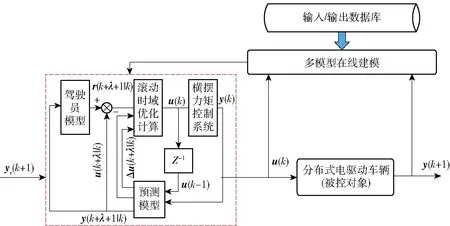
圖5 數據驅動多模型預測控制器架構Fig.5 Structure diagram of data-driven multi-model predictive controller

車輛非線性系統的局部多模型的在線建模問題可轉化為如下求解優化問題：

(21)

結合(20)式和(21)式，構建局部模型加權形式為

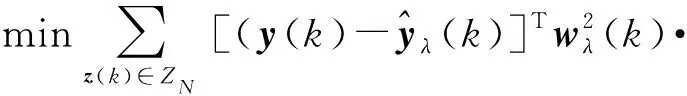
(22)

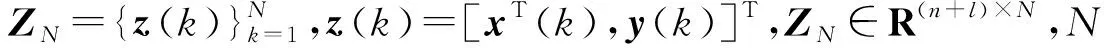
基于CARIMA模型構建車輛的局部多模型系統，其表達形式為

(23)

式中：nA、nB、nC分別為局部模型輸入量、輸出量以及噪聲干擾的階數；Aj∈Rl×l;Bj∈Rl×l;Cj∈Rl×l.

引入增量形式，將(23)式的每一個局部辨識模型轉化為

(q-1)Δy(k)=(q-1)Δu(k-1)+(q-1)ε(k)，

(24)

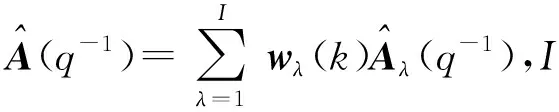
-1(q-1)(q-1)Δy(k)=
-1(q-1)(q-1)Δu(k-1)+ε(k).

(25)

為得到系統的多步預測輸出方程，引入Diophantime方程，構建基于數據驅動局部多模型車輛系統在k+j時刻的最優控制預測輸出表達式如下：

y(k+j)=Fj(q-1)y(k)+Gj(q-1)Δu(k+j-1)+
Hj(q-1)Δu(k-1)+Ej(q-1)ε(k+j)，

(26)

式中：Fj(q-1)=Fj,0+Fj,1q-1+…+Fj,nAq-nA；Gj(q-1)=G0+G1q-1+…+Gj-1q-(j-1)；Hj(q-1)=Hj,0+Hj,1q-1+…+Hj,nB-1q-(nB-1)；Ej(q-1)=E0+E1q-1+…+Ej-1q-(j-1).

基于以上分析，所構造的目標評價函數為

(27)

s.t.umin≤u(k+λ)≤umax，
Δumin≤Δu≤Δumax，
ymin≤y≤ymax，

式中：Q和R分別為被控系統輸出量和輸入量的加權矩陣；Np為預測時域；Nc為控制時域。

通過二次規劃求解過程，選取控制序列中的第1個向量作為系統的最優控制輸入量，循環滾動優化求解，得到車輛實時的附加橫擺力矩為

(28)

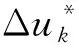
4 最優驅動力矩分配控制器設計

底層轉矩分配控制器可將附加橫擺力矩轉化為4輪最優驅動力矩，保證車輛操縱穩定性。針對極限、惡劣的越野行駛環境，本文基于輪胎縱向滑動率和輪胎垂直載荷轉移設計最優驅動力矩分配控制器。假設車輛的靜態質量均勻分布在4個車輪之間。根據轉矩平衡方程，得到各車輪的轉動力學方程為

(29)

根據(4)式和(13)式，可得到輪胎縱向滑動率動態方程如下：

(30)

分布式驅動電動車輛的4個車輪縱向驅動力矩均獨立且可控，可得到由車輛縱向力產生的橫擺力矩Mz的表達式為

(31)

車輛在越野環境下進行高速避障，考慮到路面的附著系數較低且道路起伏不定，每個車輪的垂直載荷轉移對車輛的橫向穩定性有很大的影響。因此，本文在協調各輪驅動力矩分配的過程中加入驅動輪垂直載荷轉移變量因子，4個車輪的垂直載荷表達式為

(32)

式中：Fz1、Fz2、Fz3、Fz4分別為各輪的垂直載荷。

4個車輪的垂直載荷轉移權重系數分別為

(33)

結合(26)式～(29)式，可得到考慮垂直載荷轉移的縱向滑移率狀態空間方程為

(34)

式中：S為狀態向量，S=[s1,s2,s3,s4]T；U為控制向量，U=[T1,T2,T3,T4]T；Y為輸出量，Y=Mz；Cl1、Cl2、Cl3、Cl4分別為左前輪、右前輪、左后輪、右后輪的輪胎縱向剛度。

構建的目標評價函數為

(35)

式中：e(t)表示實際狀態觀測值和期望狀態值之間的偏差；e(t)表示系統保持期望值能力的權重系數矩陣；R(t)表示控制量約束的權重系數矩陣；t0、tf分別表示積分的起始時刻和終止時刻。

為避免輪胎力進入難以控制的非線性工作區域，減少打滑現象，輪胎滑動率和輪胎側向力需要控制在一定的范圍內。同時，車輛側傾約束也是車輛操縱穩定性必須考慮的條件。由此構建的目標評價函數約束條件如下：

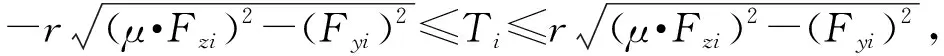
(36)

式中：Tmax為最大驅動力矩；Fymax為最大側向力；smax為最大滑移率；μ為路面摩擦系數。

基于二次規劃算法理論，將目標評價函數轉化為標準二次型從而進行最優化求解：

(37)

式中：q為目標評價函數；G、C為標準二次型向量。

最終得到控制系統4個驅動輪實時的最優驅動轉矩為

(38)

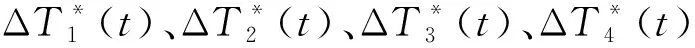
5 仿真驗證

為驗證本文分層協調操縱穩定性控制策略在提高分布式電驅動越野車的機動性和過彎橫向穩定性的有效性，基于Carsim和Simulink軟件聯合仿真平臺設計越野極限工況下的仿真實驗，進行本文提出的控制策略、無控制以及傳統MPC控制(僅考慮質心位置處的橫擺運動模式)的對比實驗驗證。車輛模型參數如表1所示。

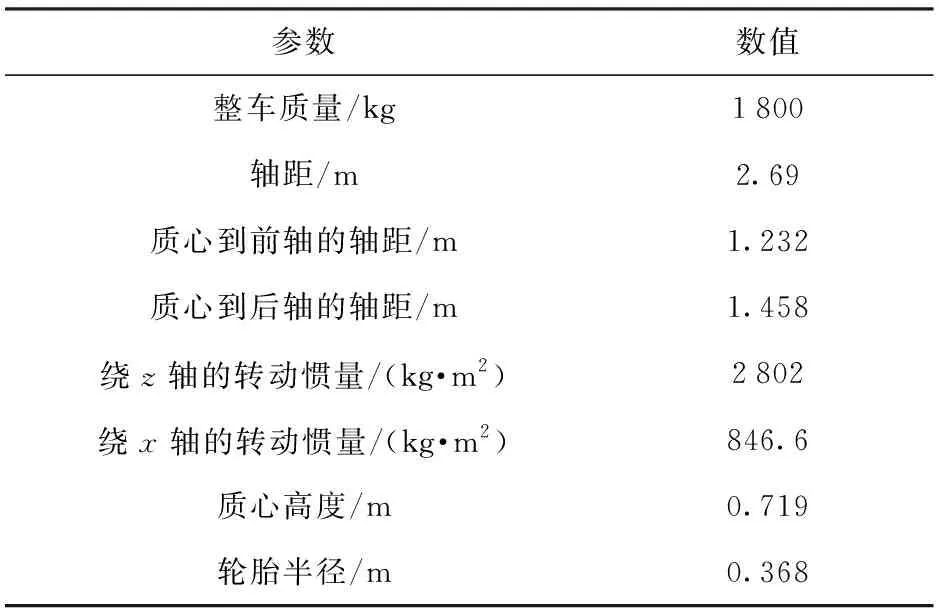
表1 車輛模型參數Tab.1 Vehicle model parameters

5.1 實驗場景1

為驗證車輛在極限工況下的高速避障穩定性和高機動性，選取標準雙移線工況作為實驗工況，車速設定為90 km/h，路面附著系數設定為0.35. 圖6表示3種控制方式下車輛的軌跡跟蹤能力。由圖6可知：無控制的車輛出現較大側滑，行駛軌跡嚴重地偏離期望軌跡，車輛處于失控狀態；基于傳統MPC的車輛基本可以保證安全行駛，但是在轉彎處也出現了較大的超調；基于本文控制策略，車輛跟蹤期望軌跡的準確度明顯提升，最大橫向偏離，具有較強的過彎姿態修正能力，基本沒有出現過大的側滑、甩尾的情況。由圖7可知，相比于傳統MPC，基于本文控制策略的車輛方向盤轉角輸入量更小其平滑，避免了過多轉向，提高了乘車舒適性和安全性。圖8和圖9表示3種控制方式下車輛橫擺角速度和質心側偏角的對比情況，相比于傳統MPC，基于本文控制策略的車輛實際橫擺角速度和質心側偏角更準確且迅速地跟蹤期望值，車輛操縱穩定性明顯提高。而無控制的車輛在此實驗工況下已完全超出穩定區間，發生失穩的危險。圖10表示車輛實時的零力矩點偏離情況，從中可知基于本文控制策略的車輛在橫向穩定性控制中充分考慮到了車輛容易發生側傾的情況，更有效地控制了零點力矩偏離距離。在圖11中，基于本文控制策略，分布式電驅動車可根據實際行駛狀態來實時調整各輪的驅動力矩，且輸出量較為平滑，保持在合理的范圍內，具有較高的機動性能。實驗結果進行量化比較，3種控制方式的控制偏差量如表2所示。

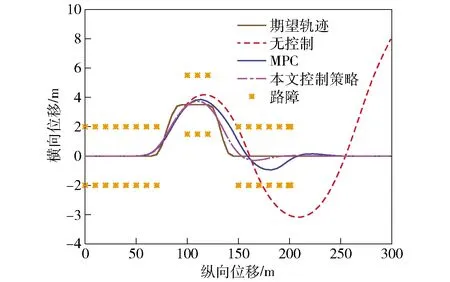
圖6 車輛軌跡Fig.6 Vehicle trajectory

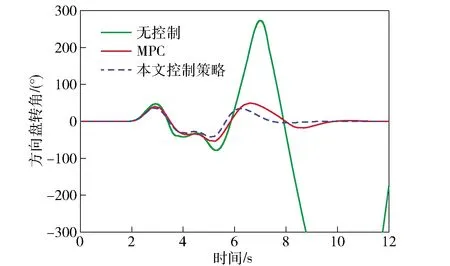
圖7 方向盤轉角Fig.7 Steering wheel angle

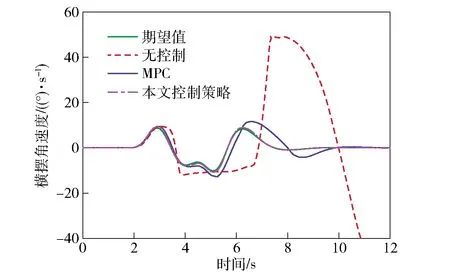
圖8 橫擺角速度Fig.8 Yaw rate

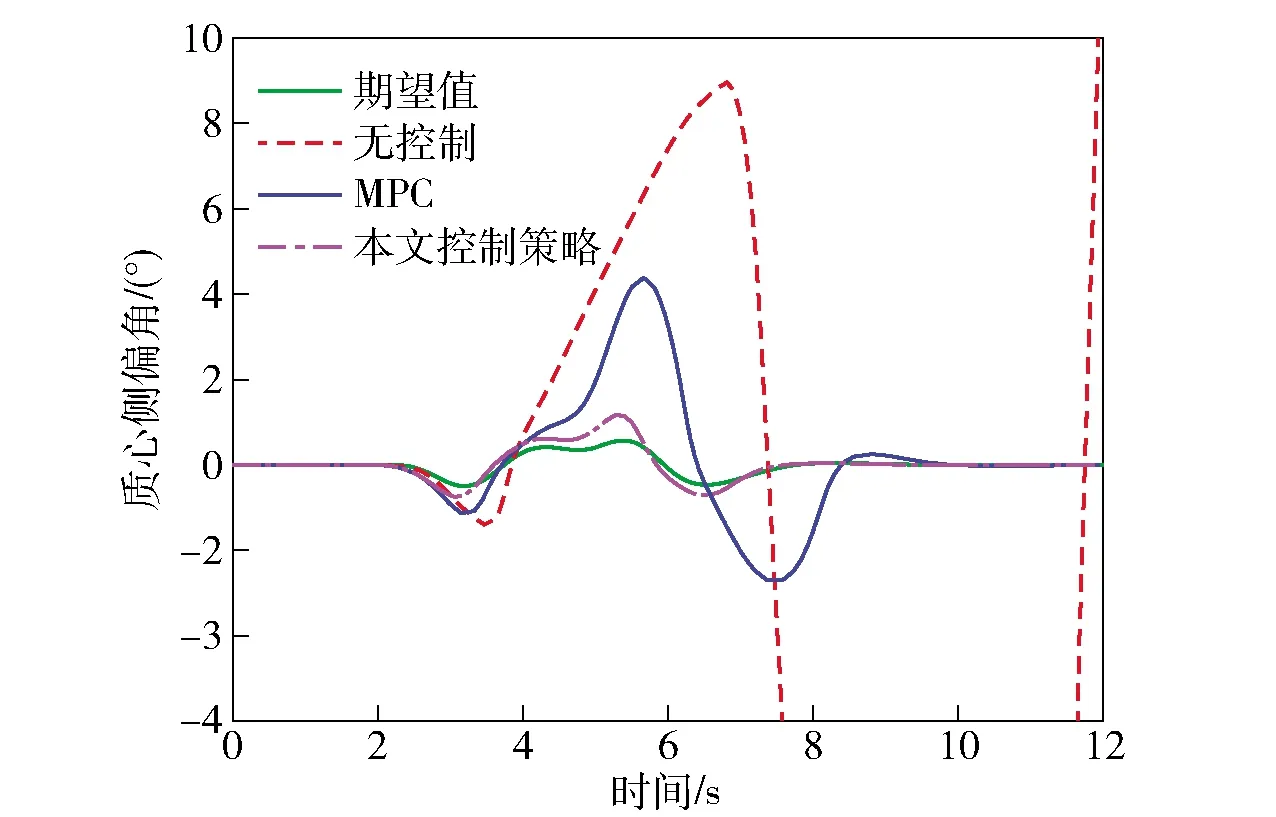
圖9 質心側偏角Fig.9 Sideslip angle

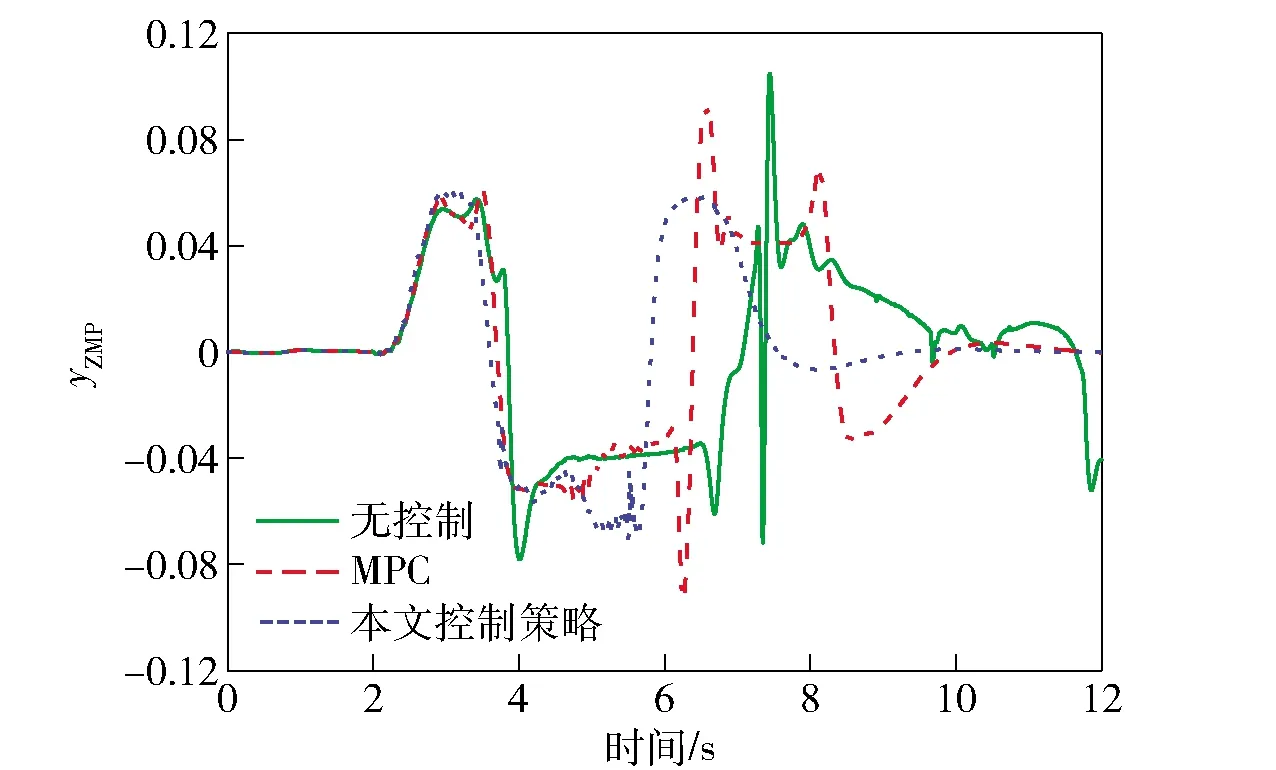
圖10 零力矩點偏離距離Fig.10 Distance from the zero-moment point

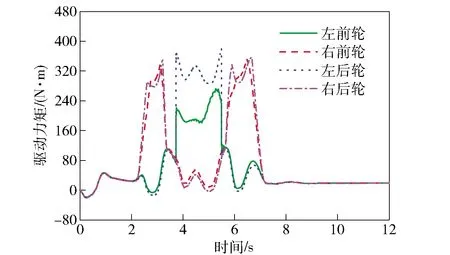
圖11 4輪轉矩優化分配Fig.11 Four-wheel torque optimization distribution

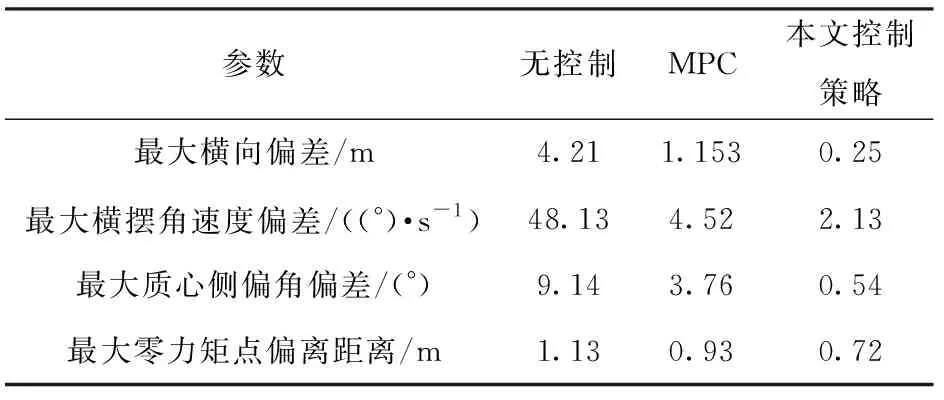
表2 場景1仿真實驗結果Tab.2 Simulation test results of Scenario 1

5.2 實驗場景2

為驗證車輛在具有時變道路曲率和側向坡度角的低附著越野工況下的操縱穩定性，構建越野環境實驗工況，選擇Carsim自帶的Alt 3 from FHWA工況，實驗環境和道路側向坡度如圖12所示。實驗車速設定為96 km/h，路面附著系數設定為0.5.

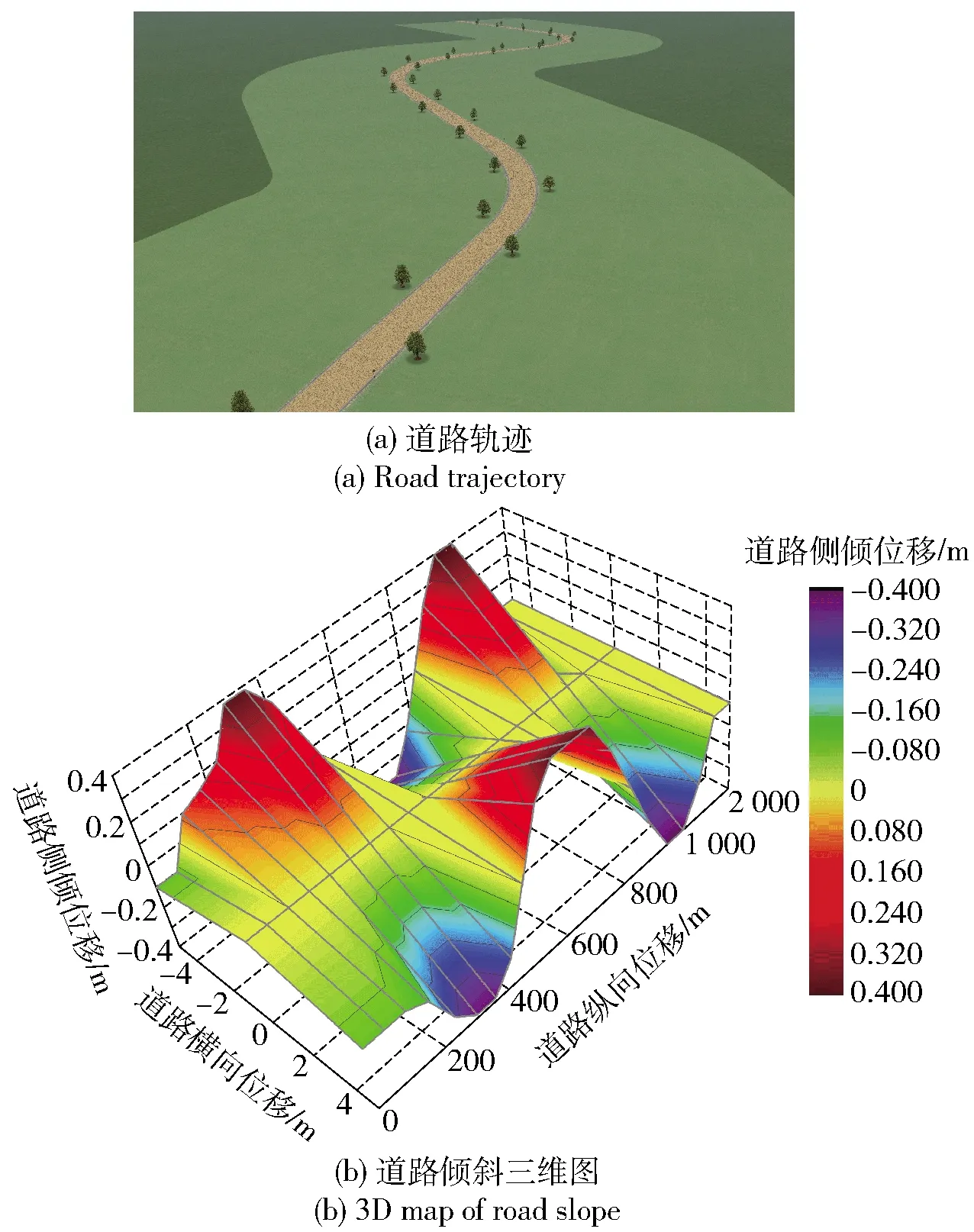
圖12 實驗道路Fig.12 Test road

由圖13和圖14可知，基于傳統MPC的車輛在大曲率彎道、傾斜越野路面的轉向過程中較容易發生側滑等危險。在縱向坐標800 m處車輛偏離了期望的軌跡，方向盤轉角輸入量出現超調現象，控制效果不理想。而本文控制策略充分考慮了路面信息以及車輛過彎姿態信息，軌跡跟蹤的準確度明顯提升，方向盤轉角輸入量更加平穩。由圖15和圖16可知，相比于傳統MPC，本文控制策略可以在極限越野工況下保證實際橫擺角速度和質心側偏角穩定在理想范圍內，過彎橫向穩定性明顯提高。由圖17可知，相比于傳統MPC，基于本文控制策略的車輛可有效減小零力矩點偏離的距離，改善了越野車輛在極限工況下的側傾穩定性。圖18表示基于本文控制策略的各輪驅動力矩分配情況，可靈活且最優地得到實時驅動力矩最優值，高效提高了分布式電驅動越野車的機動性和過彎橫向穩定性。將實驗結果進行量化比較，3種控制方式的控制偏差量如表3所示。

圖13 車輛軌跡Fig.13 Vehicle trajectory

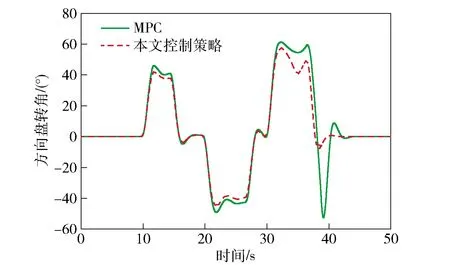
圖14 方向盤轉角Fig.14 Steering wheel angle

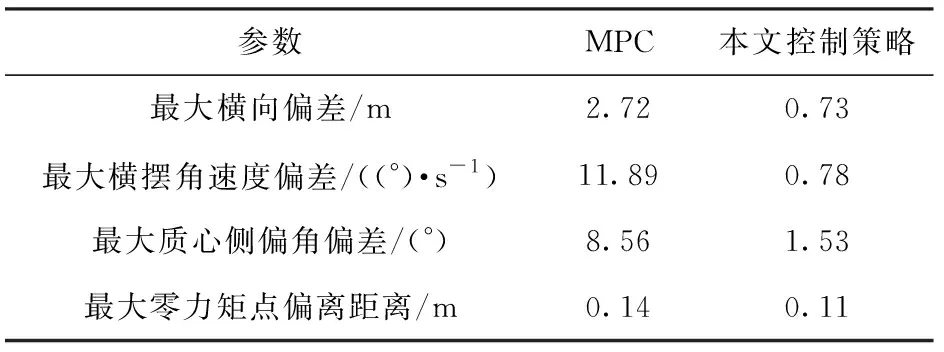
表3 場景2仿真實驗結果Tab.3 Simulation test results of Scenario 2

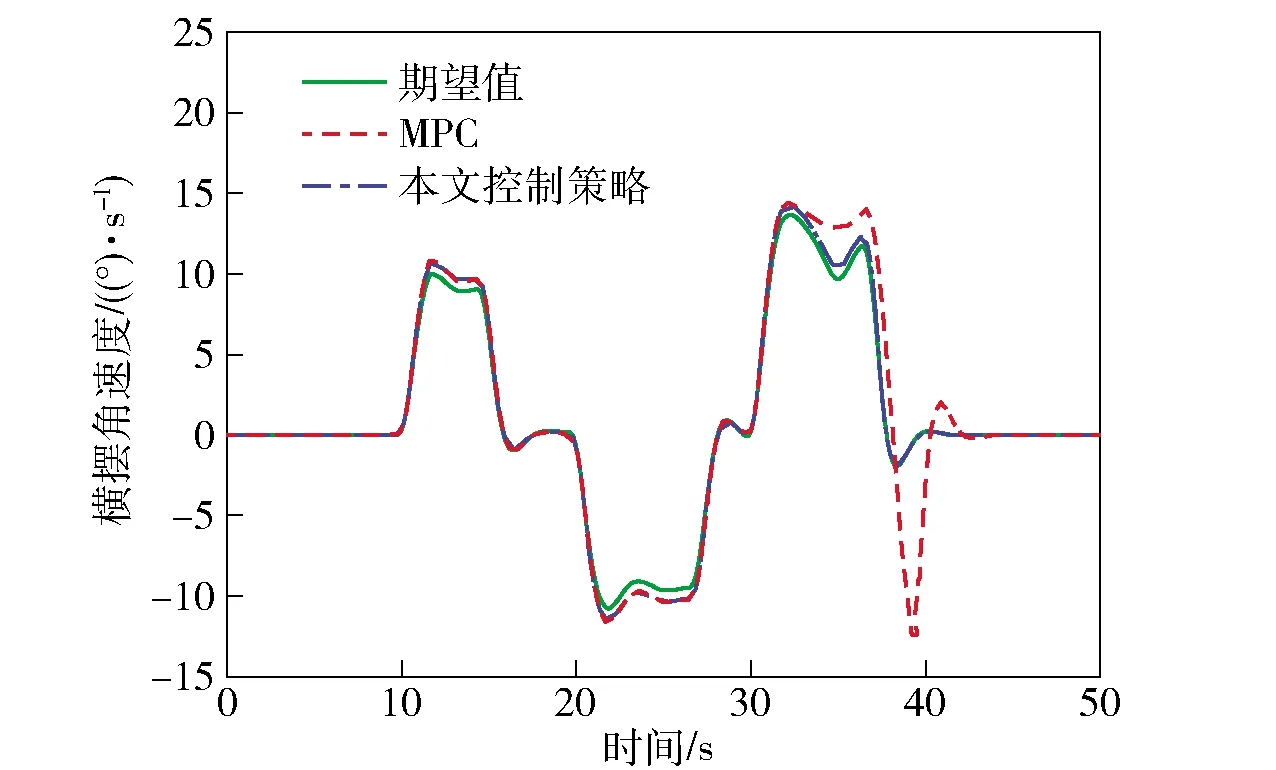
圖15 橫擺角速度Fig.15 Yaw rate

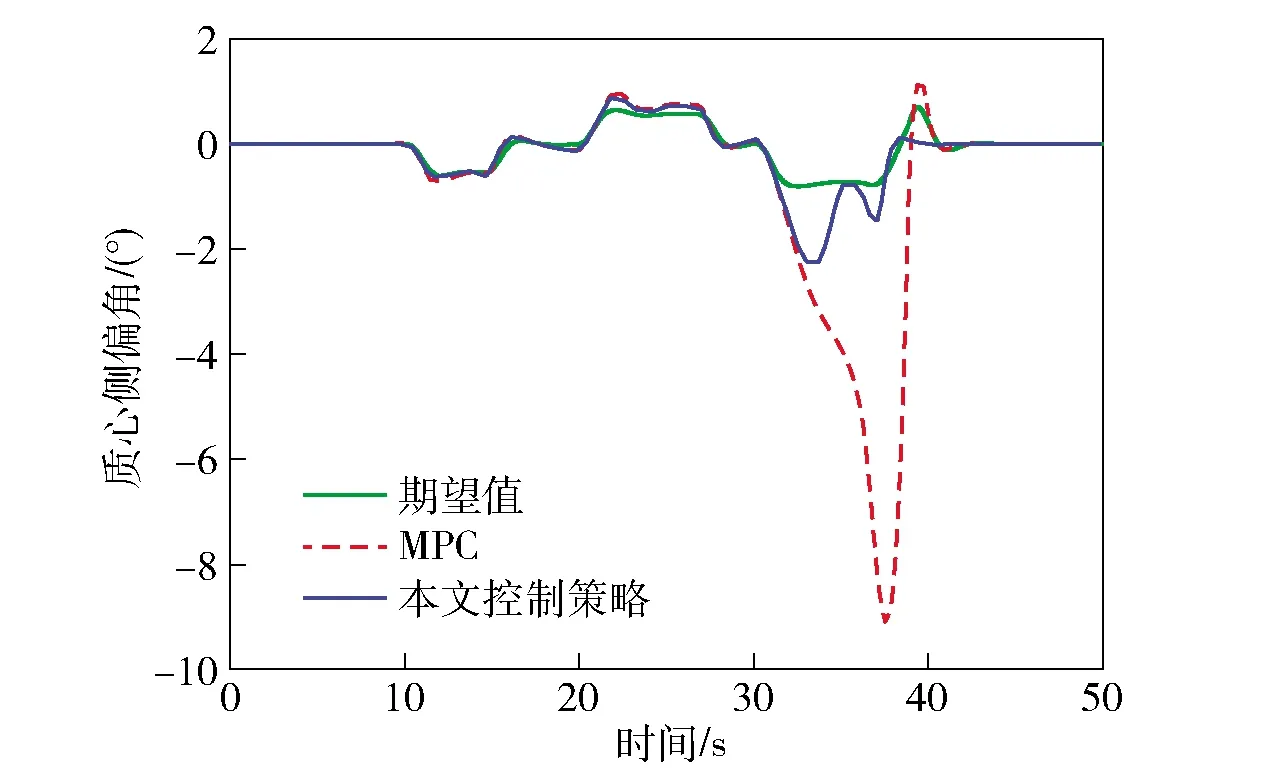
圖16 質心側偏角Fig.16 Sideslip angle

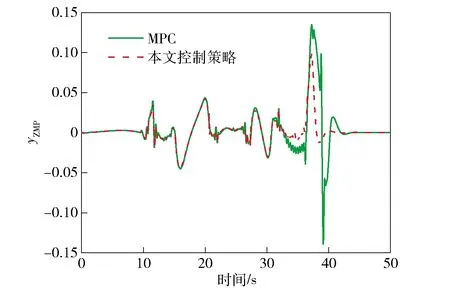
圖17 零力矩點偏離距離Fig.17 Distance from the zero-moment point

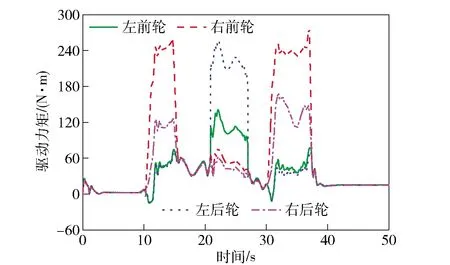
圖18 4輪轉矩優化分配Fig.18 Four-wheel torque optimization distribution

6 結論

本文以極限越野環境下分布式電驅動車輛為研究對象，提出了一種充分考慮道路信息和車輛過彎姿態信息的分層協調操縱穩定性控制策略，并通過Carsim和Simulink聯合仿真平臺驗證策略的有效性。得到以下主要結論：

1)細化并重構了車輛橫擺運動動力學方程，由于車輛橫向失穩狀態下存在不同程度的車身軌跡偏離，提出一種繞車輛質心處和前軸中心處的雙層融合型附加橫擺力矩協調控制方法，解決了傳統控制方式過于保守或是激進，無法在車輛極限失穩危險情況下實現最優車身姿態修正反饋的問題，最大程度地發揮了分布電驅動車輛的避障機動性和路徑保持能力。

2)考慮到越野工況存在時變道路曲率和側向坡度角，在橫向穩定性控制基礎上加入側傾穩定性約束條件，提出一種基于數據驅動多模型測控制的橫擺、側傾運動集成協調控制方法，改善了主動安全控制系統對極限工況的自適應能力，提高了車輛在復雜越野工況下的轉向機動性和橫向穩定性。

3)考慮到極限越野環境下路面附著系數較小以及路面顛簸，車輛高速轉彎極易發生側翻、側滑甩尾等危險，本文基于輪胎滑動率和垂直載荷轉移反饋信息獲得最優的各輪驅動力矩控制量，最大程度地發揮了分布式電驅動越野車的快速通過能力和行駛穩定性能。