基于路面自適應的多輪輪轂電機驅動車輛驅動防滑控制

陳路明， 廖自力， 張征

(1.陸軍裝甲兵學院 兵器與控制系, 北京 100072; 2.國民核生化災害防護國家重點實驗室, 北京 102205)

0 引言

驅動力控制系統是一類較為典型的車輛行駛控制系統，這種系統一般以驅動防滑控制(ASR)為核心，在車輛起步、加速等行駛工況，對車輪滑轉狀態進行調整，改善車輛的動力性能和穩定性[1]。與傳統汽車相比，輪轂電機驅動車輛各個執行器相互獨立，可直接控制電機轉矩輸出，這類車輛在ASR系統設計方面具有一定的優勢[2]。目前，國內外學者為電驅動車輛設計了很多種驅動力控制系統，大多數都采用了基于滑轉率的控制方法[3-4]。文獻[5]和文獻[6]分別將模糊控制和自抗擾控制應用于車輛油門和制動控制器中，進行牽引力控制。為了提高驅動轉矩控制的精度，文獻[7]設計了一種基于滑模控制方法的驅動防滑系統，根據車輛單輪受力模型和滑動模態函數，推導了車輪防滑控制所需的驅動力等效控制量。這些系統大多面向4輪驅動的民用電動車輛，一般只能適應單一的道路環境，缺乏控制器對路面變化的適應性研究。實際上，與4輪驅動車輛相比，多輪輪轂電機驅動車輛的行駛工況通常更為惡劣，需要在低附著路面、變附著路面條件下保持良好的機動能力，有時還要面臨急加速行駛，越野行駛等特殊工況[8]，因此需要根據多輪車輛結構配置和操縱性特點，設計具有路面自適應功能的控制系統。

道路識別的關鍵是路面附著系數估計，路面附著系數影響輪胎與道路之間的作用力，并決定車輛行駛的最佳滑轉率[9]。路面識別方法可以分為兩類：基于試驗的方法和基于模型的方法[10-11]。基于試驗的方法一般使用了光學和聲學傳感器，在良好的測試條件下具有較高精度，然而這些傳感器的可靠性很容易受到駕駛條件和外部環境的影響[12]。基于模型方法通常依賴輪胎模型采用濾波方法估計車輛狀態參數和路面附著系數，由于車輛行駛時影響滑轉率計算精度的因素很多，提高抗干擾性和魯棒性是基于模型方法研究的難點問題[13]。

本文設計了一種具有路面自適應功能的多輪輪轂電機驅動車輛ASR系統。用衰減記憶無跡卡爾曼濾波(FM-UKF)法[14]對路面附著系數進行估算，然后改進滑模控制(SMC)方法，設計模糊滑模控制(FSMC)器根據路面辨識結果進行ASR，使車輛在路面動態變化條件下也能具備較好地動力性和穩定性。最后，在基于dSPACE系統的實時仿真平臺上設計不同工況的車輛行駛仿真實驗。

1 車輛系統建模

1.1 非線性3自由度車輛模型

忽略空氣阻力，將滾動阻力線性化處理，分別建立研究對象雙軌3自由度車輛模型和車輪受力分析模型[15]，分別如圖1和圖2所示。圖1中：v為車輛速度；vx、vy分別為車輛縱向速度、側向速度；β為質心側偏角；γ為橫擺角速度；Fxil、Fxir分別為第i軸左、右兩側車輪縱向力，Fyil、Fyir分別為第i軸左、右兩側車輪側向力，i=1,2,3,4；δil、δir分別為第i軸左、右兩側車輪轉向角；αil、αir分別為第i軸左、右兩側車輪側偏角；Ld為輪距；Li為第i軸與質心處的距離。圖2中：m為車輛質量；g為重力加速度；ω為車輪輪速；Td為驅動力矩；Mf為滾動阻力矩；Fx為車輪縱向力；Fz為車輪垂直載荷。

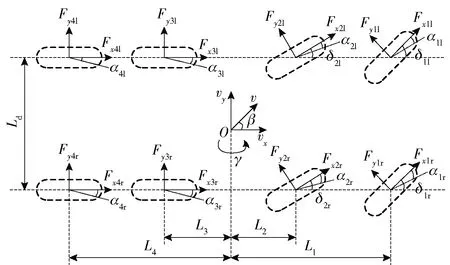
圖1 3自由度車輛模型Fig.1 3-DOF dynamics model of vehicle

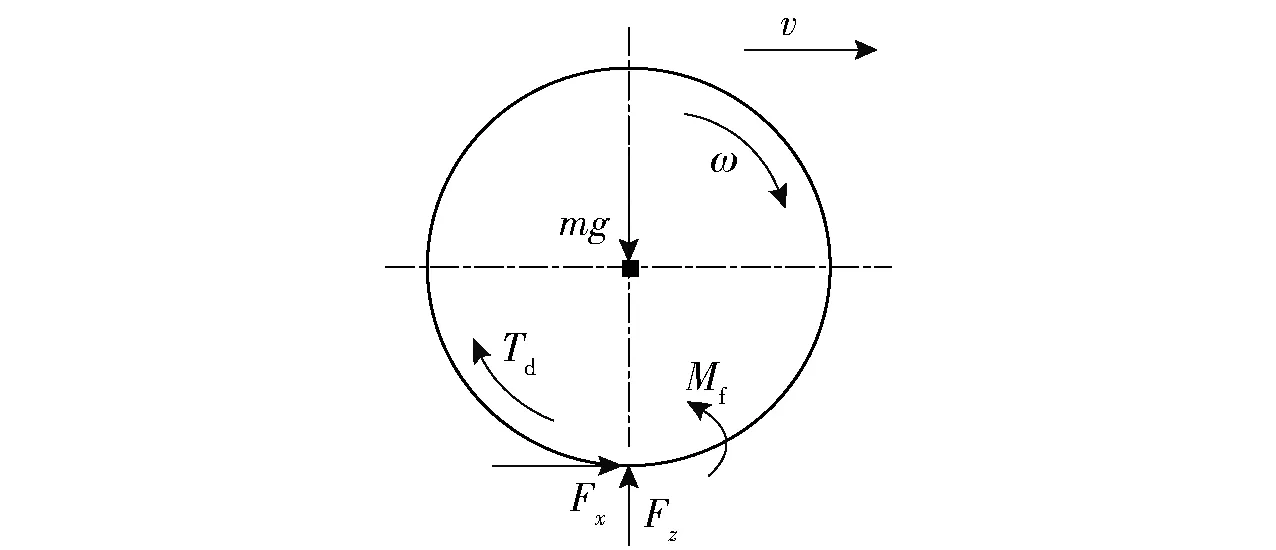
圖2 車輪受力圖Fig.2 Wheel force analysis

根據車輛動力學，平衡方程為

max=-Fy1lsinδ1l+Fx1lcosδ1l-Fy1rsinδ1r+
Fx1rcosδ1r-Fy2lsinδ2l+Fx2lcosδ2l-
Fy2rsinδ2r+Fx2rcosδ2r+Fx3l+Fx3r+Fx4l+Fx4r，

(1)

may=Fy1lcosδ1l+Fx1lsinδ1l+Fy1rcosδ1r+
Fx1rsinδ1r+Fy2lcosδ2l+Fx2lsinδ2l+
Fy2rcosδ2r+Fx2rsinδ2r+Fy3l+Fy3r+Fy4l+Fy4r，

(2)

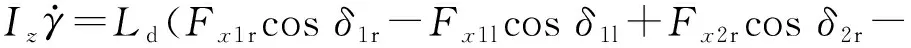
(3)

式中：ax、ay分別為車輛縱向加速度、側向加速度；Iz為橫擺轉動慣量。

1.2 車輪受力模型

車輪力矩表達式為

(4)

Td=icTe，

(5)

Mf=fgFzR，

(6)

式中：I為車輪轉動慣量；R為車輪有效半徑；ic為減速器傳動比；Te為輪轂電機轉矩；fg為滾動阻力系數。

1.3 輪胎模型

Dugoff輪胎模型能夠描述車輛非線性特性，并且計算簡便，選用Dugoff輪胎模型作為ASR的輪胎模型，其表達式為

(7)

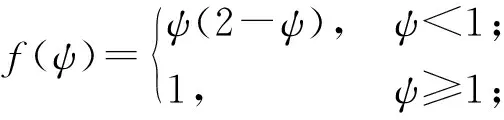
(8)

(9)

(10)

式中：Fy為車輪側向力；μ為路面附著系數；Cx、Cy分別表示縱向剛度、側偏剛度；S為滑轉率；f(ψ)為Dugoff輪胎模型的修正系數；ψ為表征輪胎力非線性特征邊界值；к為速度影響因子，與輪胎結構及材料有關，作用在于修正輪胎滑移速度對輪胎力的影響。

歸一化后，有

(11)

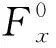
各輪側偏角近似表達式為

(12)

2 路面識別方法設計

2.1 狀態估計模型

構建狀態方程和量測方程：

(13)

式中：Xk+1和Xk分別為第k和第k+1時刻狀態變量；g(·)和h(·)分別為狀態方程中的非線性函數和觀測函數；u為輸入向量；wk、vk均為噪聲；Yk為第k時刻量測變量。

狀態變量為

X=[μ1l,μ1r,μ2l,μ2r,μ3l,μ3r,μ4l,μ4r]T.

(14)

輸入向量為

u=[δ1l,δ1r,δ2l,δ2r]T.

(15)

量測變量為

Y=[ax,ay,γ]T.

(16)

根據車輛動力學，得

(17)

(18)

(19)

2.2 無跡卡爾曼濾波方法設計

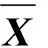
(20)

2n+1個sigma點權值為

(21)

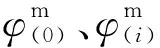
初始條件為

(22)

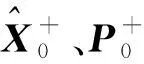
對狀態變量進行無跡變換，得到sigma點預測值，即

(23)

sigma點預測值加權后得到

(24)

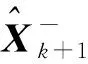
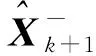
(25)

(26)

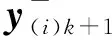
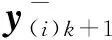
(27)

計算量測量協方差

(28)

式中：Rc為量測噪聲協方差。

X與Y協方差可表示為

(29)

Kalman濾波增益為

Kk+1=P(Y,Y)[P(X,Y)]-1.

(30)

更新得

(31)

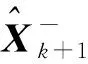
2.3 FM-UKF估計方法設計

傳統無跡卡爾曼濾波(UKF)法是一種無限增長記憶濾波方法，這種方法非常容易受到模型精度的影響，導致濾波誤差激增甚至發散等現象[16]。因此，引入指數衰減記憶因子，設計FM-UKF法修正估計值誤差。

取k-i=N，則第N時刻Kalman濾波增益為KN，在UKF法基礎上進行改進，為盡量減弱UKF法舊時刻量測值在狀態變量估計中的作用，降低N時刻以前的Kk-i值權重，加強新時刻量測值對估計方法的修正作用，突出N時刻的KN值。基于指數加權的方法，引入指數衰減忘記因子epi，其中指數表達式為

(32)

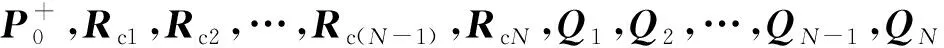
(33)

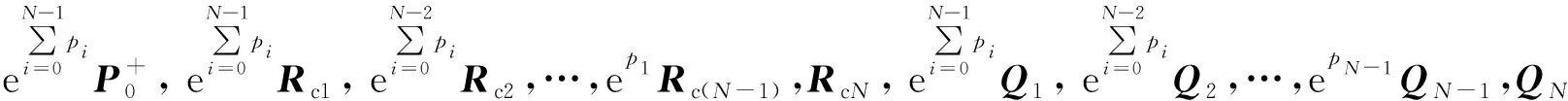
3 基于FSMC的ASR系統設計

輪胎滑轉率與路面附著系數之間存在密切關系，如圖3所示。由圖3可以看出，附著系數一般先隨滑轉率增加而增加，達到峰值后再減小。路面附著系數峰值對應的滑轉率即為最佳滑轉率。

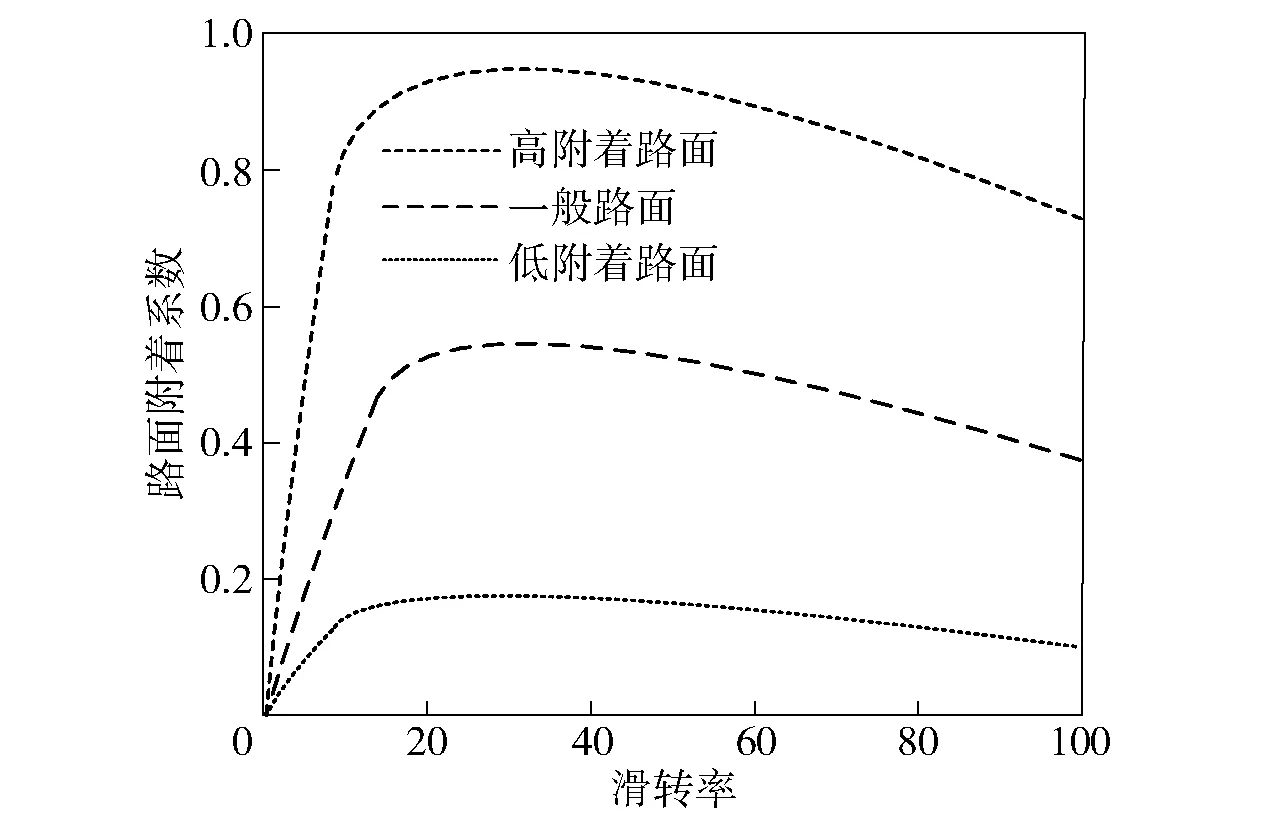
圖3 路面附著系數與滑轉率關系曲線Fig.3 Curve of relationship between road adhesion coefficient and slip ratio

實際行駛時路面總是容易變化，因此根據FM-UKF法的路面辨識結果和輪胎滑轉率與路面附著系數曲線預估當前路面最佳滑轉率，然后設計模糊滑模ASR器，對打滑車輪輪轂電機輸出轉矩進行調節，盡可能減小輪胎滑轉率與最佳滑轉率的差值。

當車輛處于驅動工況時，理論縱向滑轉率S*與實際縱向滑移率S的關系為

(34)

定義滑轉率差值：

e=S*-Sb，

(35)

式中：Sb為最佳滑轉率。

對(35)式求導，得

(36)

SMC的滑模面為

(37)

式中：c為滑模面系數。

根據(35)式～(37)式，得

(38)

式中：ε為趨近速率，且ε>0；Ω為滑模邊界值，且Ω>0.

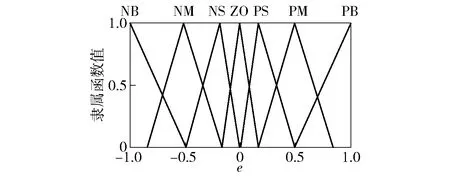
圖4 e的隸屬函數Fig.4 Membership function of input e

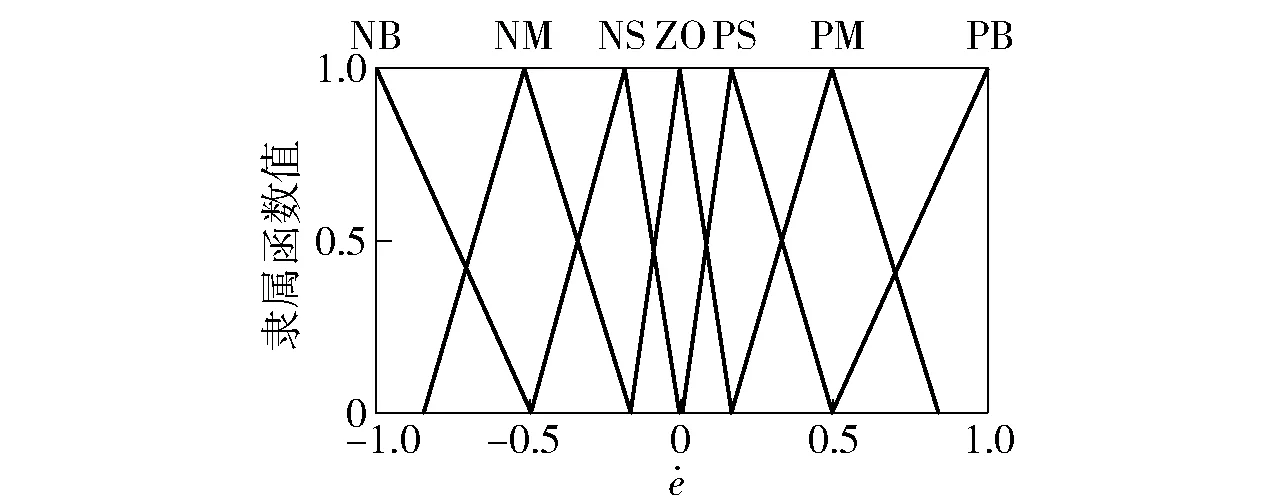
圖5 的隸屬函數Fig.5 Membership function of input

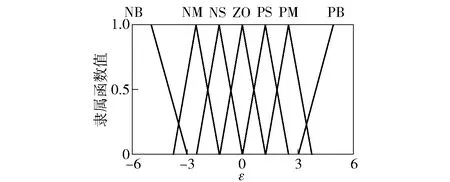
圖6 ε的隸屬函數Fig.6 Membership function of output ε

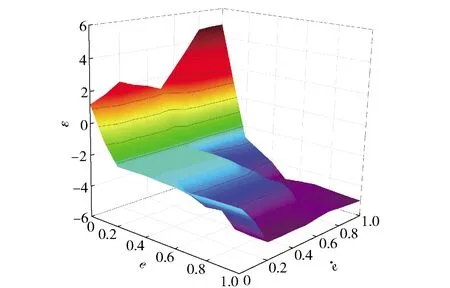
圖7 ε的三維映射圖Fig.7 Three-dimensional map of output ε

根據(10)式、(34)式和(38)式得

(39)

對(4)式求導，得

(40)

(39)式代入(40)式，根據所研究車輛的輪轂電機模型[18]，得到模糊滑模控制輸出的調節力矩，從而實現車輛ASR.

4 仿真結果及分析

在如圖8和圖9所示實時仿真平臺進行實驗，檢驗路面識別和ASR的效果。

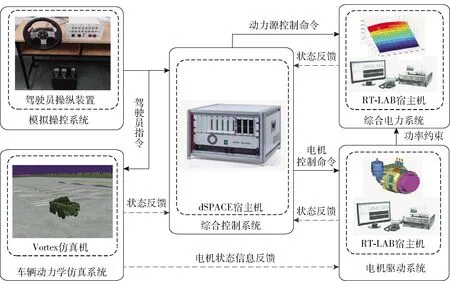
圖8 仿真平臺子系統信息交互Fig.8 Information interaction among subsystems of simulation platform

圖9 實時仿真平臺Fig.9 Overall structure of simulation platform

實驗采用的仿真實驗平臺主要由駕駛員模擬操控系統、基于Vortex(加拿大CM-LABS公司生產的一款多體動力學模擬仿真系統)的動力學仿真系統、基于RT-LAB(加拿大Opal-RT公司生產的一款工業級實時仿真系統)的綜合電力系統、基于RT-LAB的電機驅動系統和基于dSPACE(德國dSPACE公司開發的一套實時仿真系統)的綜合控制系統構成，各系統間采用Flexray總線通信。車輛主要參數如表1所示。

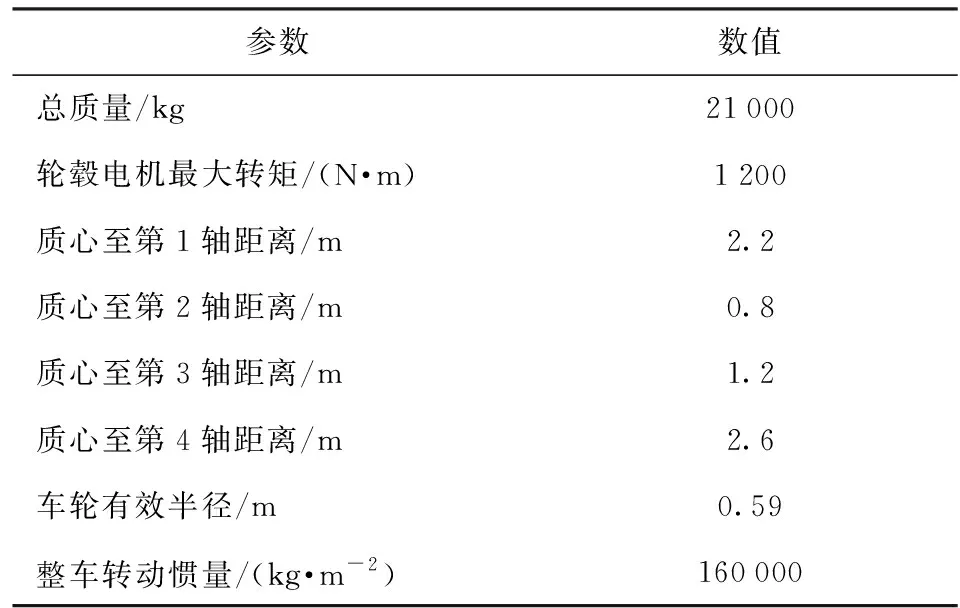
表1 車輛部分參數Tab.1 Parameters of vehicle

4.1 路面附著系數估計實驗

為了驗證不同環境和駕駛條件下的路面附著系數估計效果，設計了一般路面(μ=0.5)雙移線行駛實驗和變附著系數路面連續轉向行駛實驗，仿真結果如表2、圖10～圖13所示。

由表2及圖10～圖13可以看出，不同環境和駕駛條件下，FM-UKF法的估計值與其實際值都基本吻合，估計精度優于UKF法。

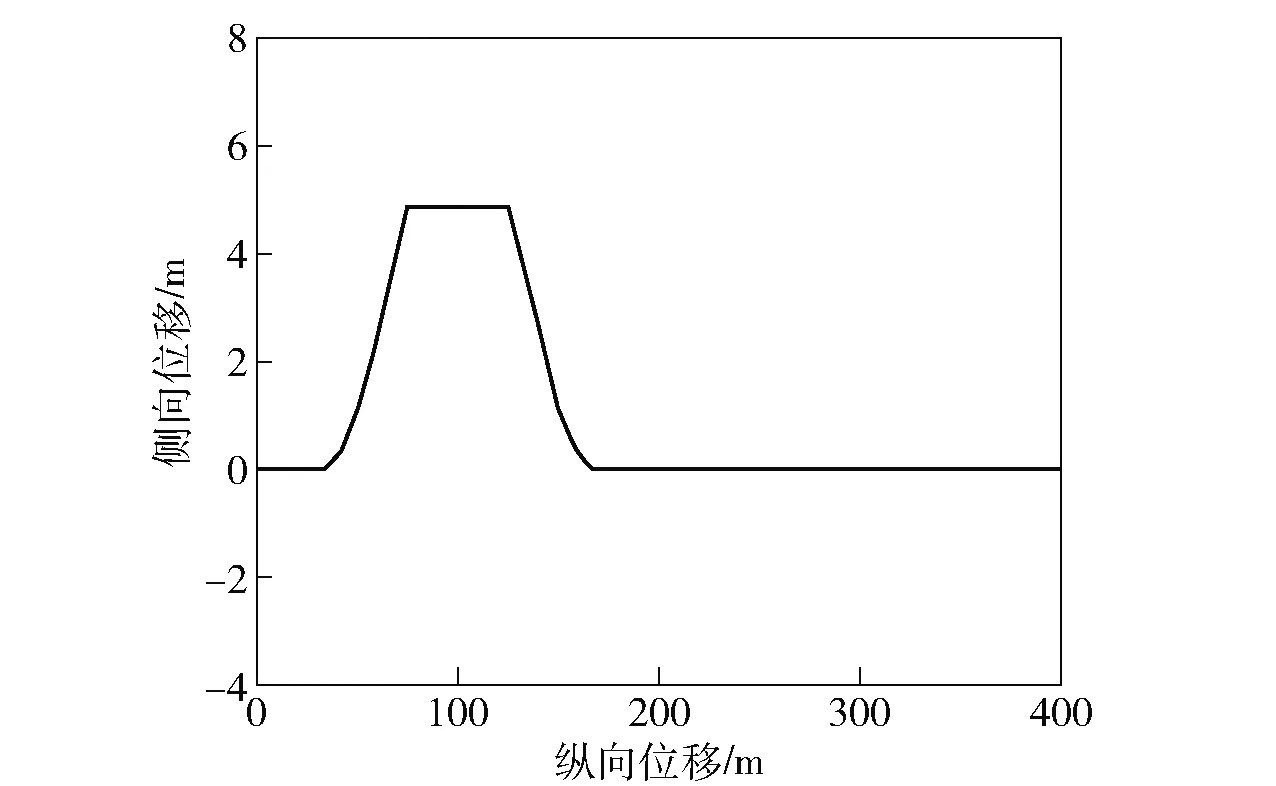
圖10 雙移線行駛的期望路徑Fig.10 Expected path on double lane

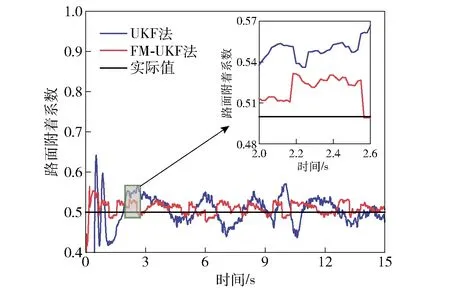
圖11 雙移線行駛路面附著系數估計Fig.11 Road adhesion coefficient estimation for double lane change driving

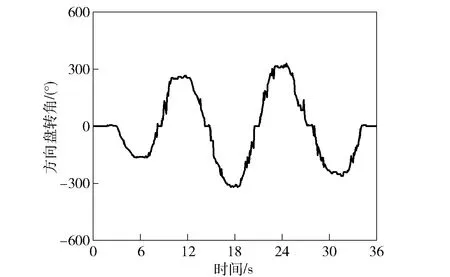
圖12 連續轉向行駛的方向盤轉角Fig.12 Steering wheel angle for continuous steering

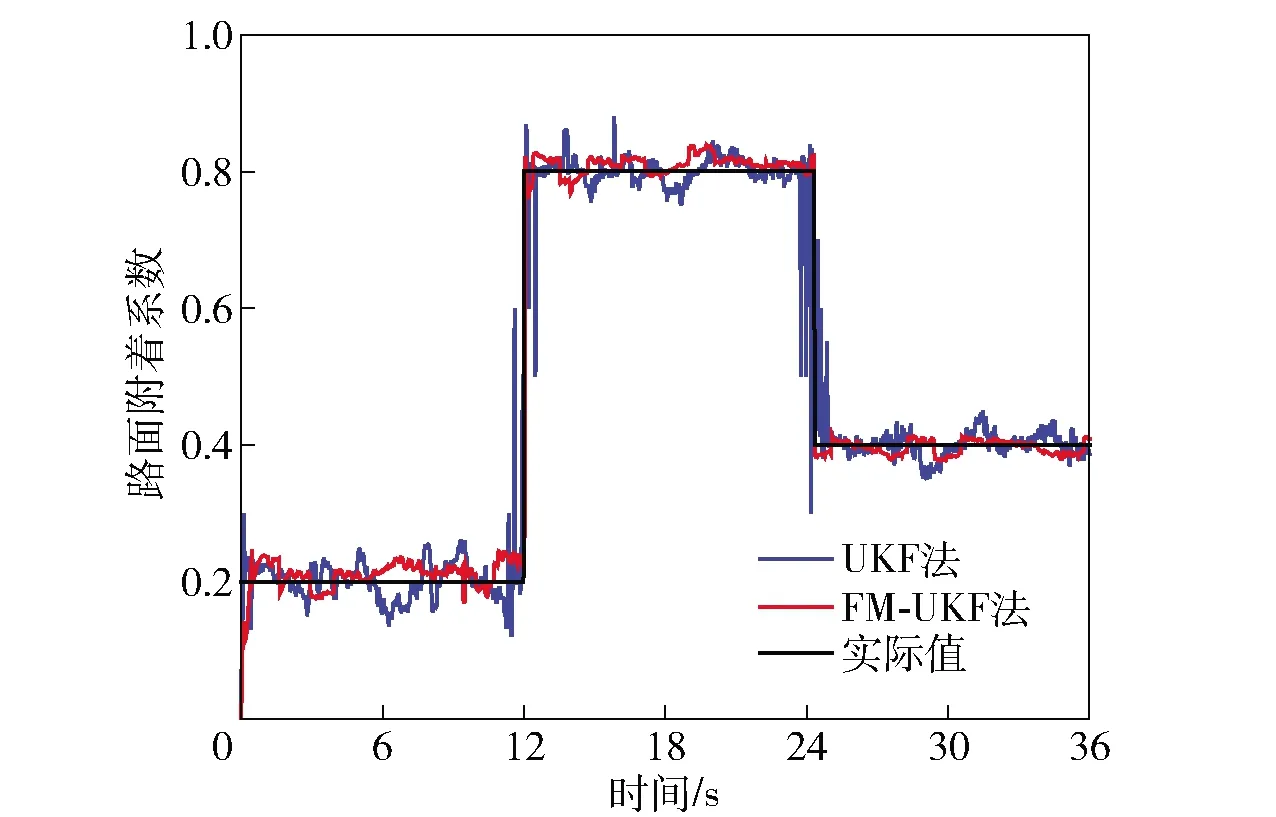
圖13 連續轉向行駛路面附著系數估計Fig.13 Road adhesion coefficient estimation for continuous steering

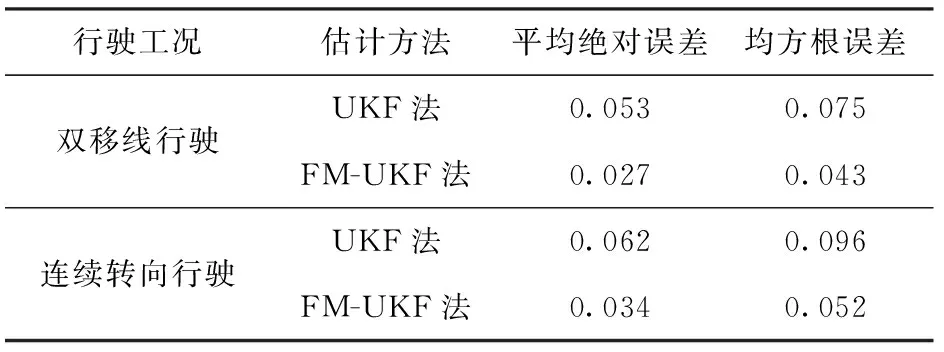
表2 路面附著系數估算誤差統計Tab.2 Estimated error statistics of road adhesion coefficients

4.2 ASR實驗

為了驗證控制策略在不同行駛工況下的驅動力控制效果，設計了表3所示3種典型道路實驗。

4.2.1 低附著系數路面行駛實驗

依照表3中實驗工況1設置仿真條件，選取路面附著系數估算誤差的平均絕對誤差和均方根誤差作為評價指標，不同估計方法的誤差結果如表4所示，部分關鍵過程參數如圖14～圖16所示。

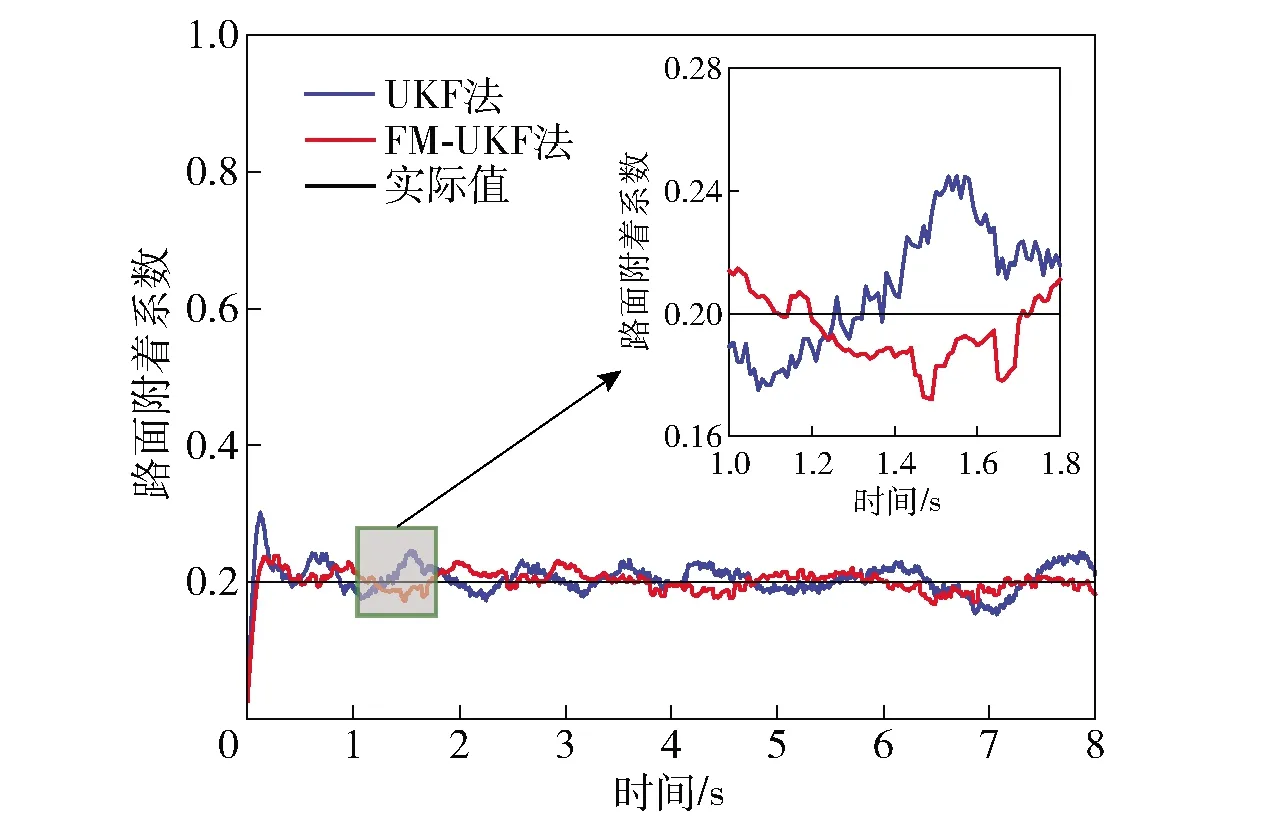
圖14 工況1的路面附著系數估算對比Fig.14 Road adhesion coefficient estimation under Condition 1

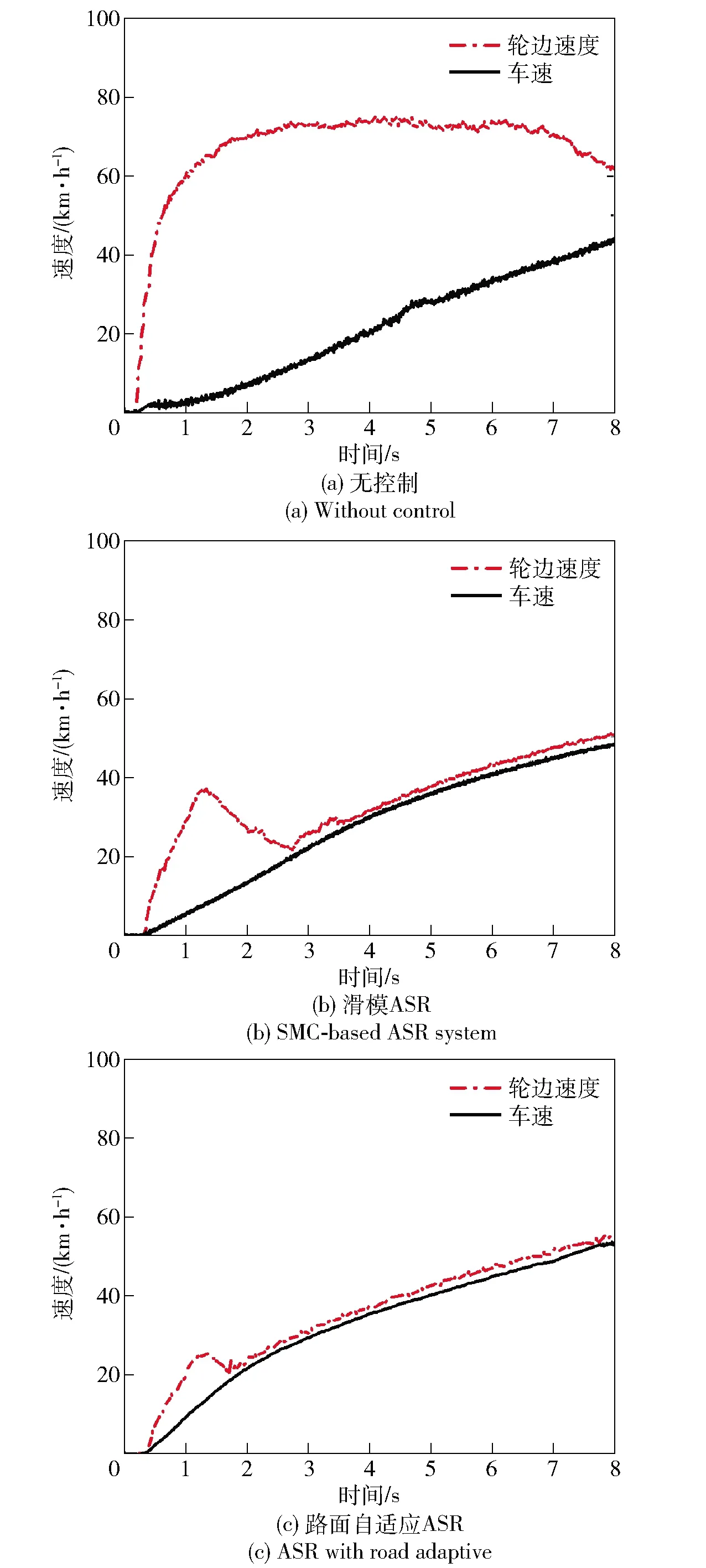
圖15 工況1的車速與輪邊速度Fig.15 Vehicle speed and wheel speed under Condition 1

圖16 工況1的車輪滑轉率Fig.16 Slip ratio under Condition 1

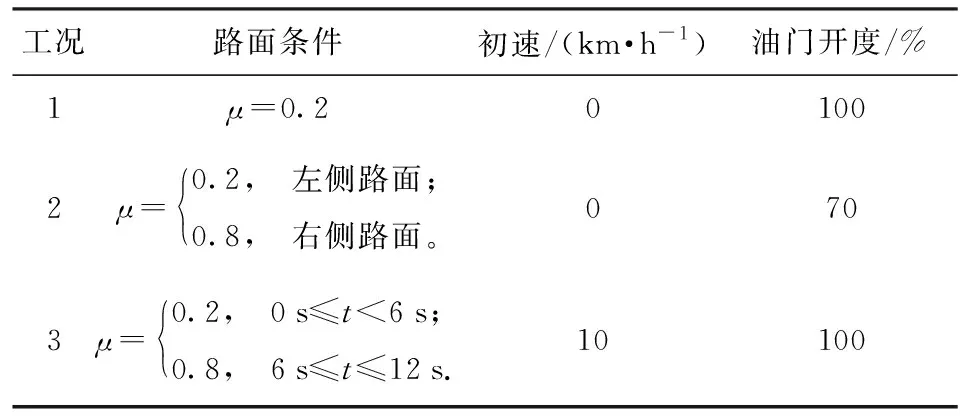
表3 ASR實驗條件設置Tab.3 Simulation conditions of ASR

由表4和圖14可知，UKF法和FM-UKF法都能對單一道路的路面附著系數進行有效估計，但FM-UKF法具有更高的估計精度。由圖15可以看出，當車輛未施加驅動力控制時，輪胎打滑嚴重，輪邊速度迅速增加，整個行駛過程中輪邊速度明顯高于車速。基于SMC的ASR系統有效減小了輪邊速度與車速之間的差異，驅動輪打滑現象得到了一定程度的抑制。而采用路面自適應ASR后，車輪打滑情況得到了更快、更明顯的抑制，加速過程中未出現過度滑轉現象，輪邊速度和車速大致接近。另外與無驅動力控制狀態相比(加速至43 km/h)，施加控制后，車輛在相同時間內加速至52 km/h，動力學性能得到了提高。

表4 低附著系數路面估算誤差統計Tab.4 Estimated error statistics of low-adhesion road

由圖16(a)可知，當車輛不受驅動力控制時，驅動輪實際滑移率與當前道路最佳滑移率相差較大，起步階段平均滑轉率誤差大于85%，嚴重影響車輛動力性能。圖16(b)表明，在驅動輪發生嚴重打滑時，基于SMC的ASR系統對輪胎滑轉率進行了控制，實際滑轉率在最佳滑轉率附近波動，但平均誤差較大，并且出現一定程度的抖振現象。從圖16(c)可以看出，采用路面自適應ASR后，實際滑轉率更加趨近于最佳滑轉率，并且改善了傳統滑模控制的抖振問題，控制效果更加明顯。

4.2.2 對開路面行駛實驗

依照表3中的實驗工況2設置仿真條件，實驗結果如表5及圖17～圖21所示。

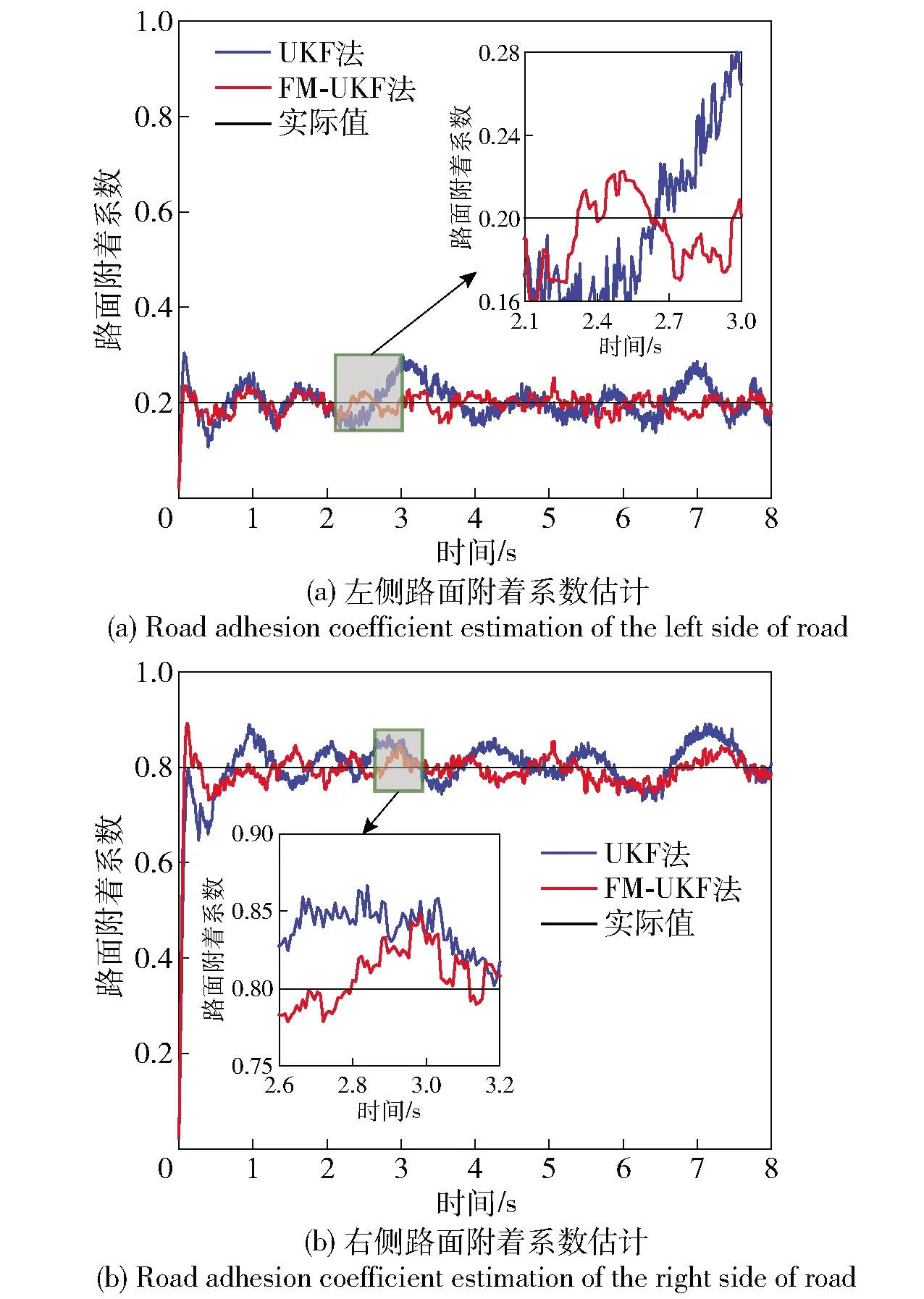
圖17 工況2的路面附著系數估算對比Fig.17 Road adhesion coefficient estimation under Condition 2

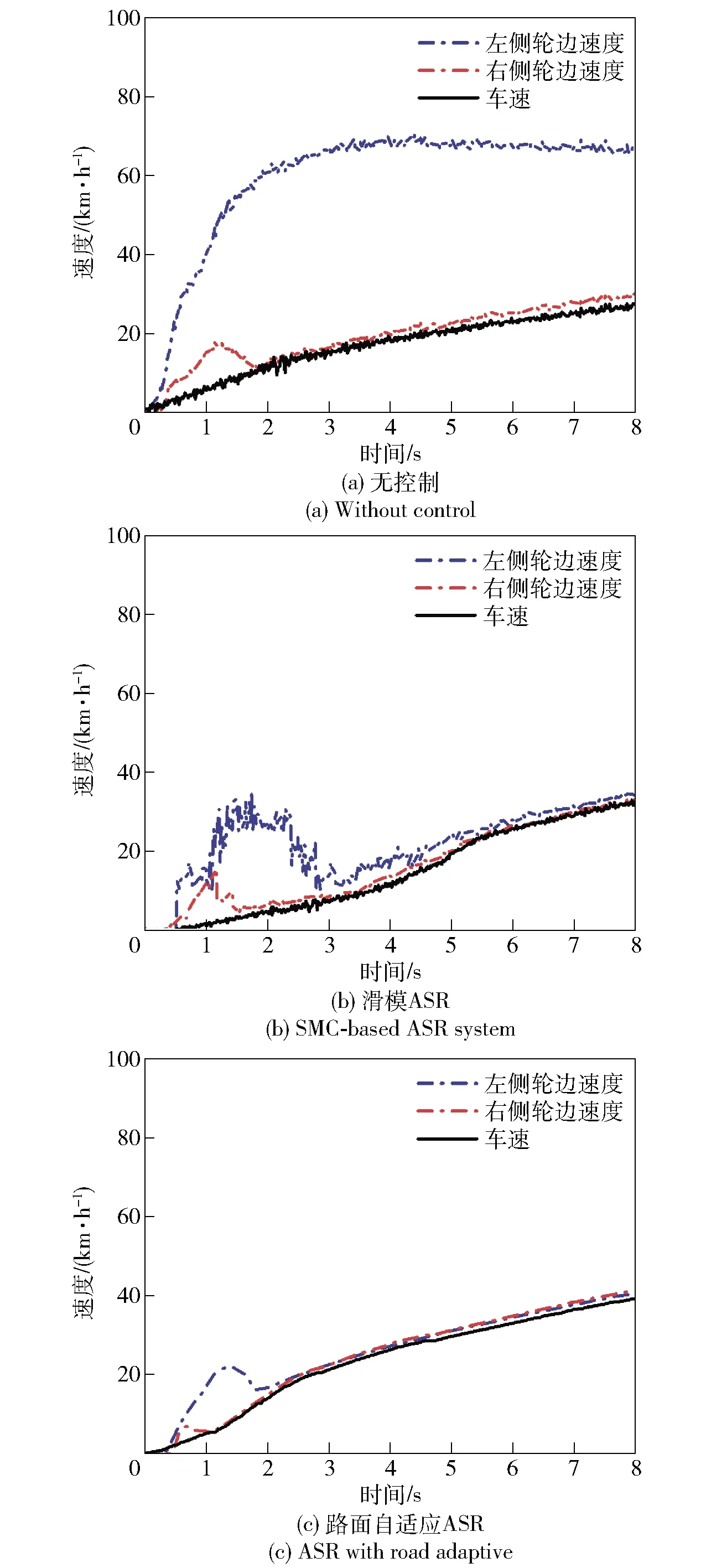
圖18 工況2的車速與輪邊速度Fig.18 Vehicle speed and wheel speed under Condition 2

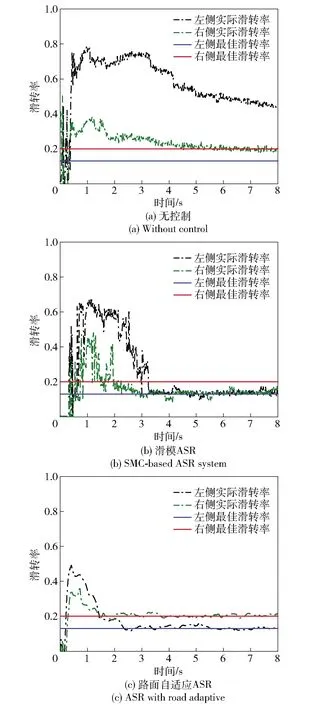
圖19 工況2的車輪滑轉率Fig.19 Slip ratio under Condition 2

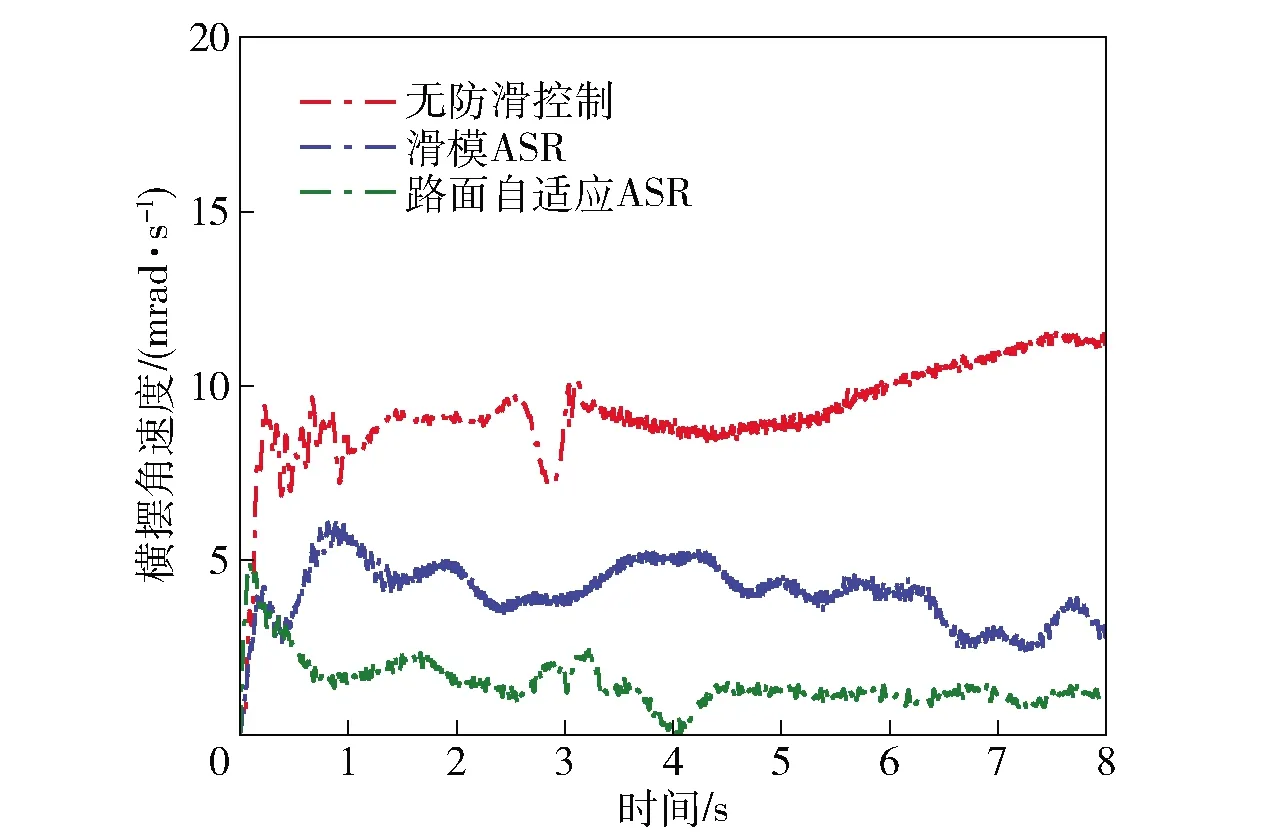
圖20 對開路面車輛橫擺角速度Fig.20 Yaw rate of vehicle on μ-split road

圖21 對開路面車輛運行軌跡Fig.21 Vehicle track on μ-split road

表5和圖17表明，與UKF法相比，FM-UKF法更能準確識別左右兩側路面附著系數的差異，FM-UKF法估計值更接近實際值。由圖18可以看出，當兩側路面附著系數不同時，無驅動力控制的車輛左右側車輪輪邊速度差異很大：左輪在低附著系數路面上運動，打滑現象比較明顯，輪邊速度迅速增加；而右輪在相對良好的路面上行駛，打滑現象相對較輕，輪邊速度較為平穩地增加。采用基于SMC的ASR系統后，驅動輪過度打滑現象得到了控制，車輛兩側輪邊速度的差異變小。路面自適應驅動防滑控制系統則根據路面識別結果分別對兩側車輪的輪邊速度進行了有效調整。

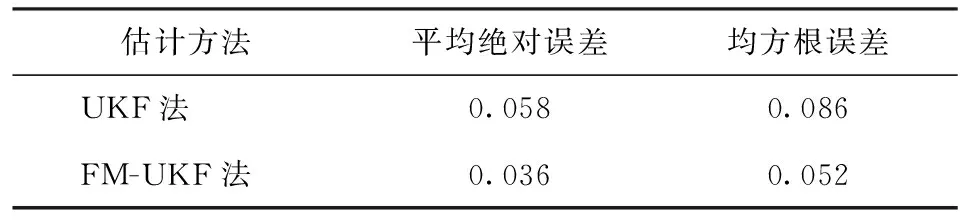
表5 對開路面估算誤差統計Tab.5 Estimated error statistics of μ-split road

由圖19可知，對于未施加驅動力控制的車輛，左右側車輪實際滑移率相差很大：左側路面條件較差，車輪實際滑轉率明顯高于最佳優滑轉率；而右側路面條件較好，雖然車輛起步時打滑較為嚴重，但整體趨勢上右側車輪滑轉率與最佳滑轉率間的誤差較小。采用基于SMC的ASR系統后，兩側車輪打滑現象均得到了一定的抑制，但這種系統不能根據對開路面特點對兩側車輪滑轉率進行不同地調整，并且系統波動較大，控制效果不太穩定。路面自適應ASR系統在車輛行駛過程中準確識別了兩側路面附著系數差異，根據路況合理減小兩側車輪滑轉率與相應最佳滑轉率的偏差，有效提高了車輛驅動能力，另外采用路面自適應ASR系統的車輛動態參數波動較小，控制效果較好。

圖20和圖21表明，在對開路面加速時，無驅動力控制狀態下車輛最大橫擺角速度達到11 mrad/s左右，側向位移持續增大到2.49 m，出現了行駛軌跡偏離現象，嚴重影響了車輛操縱穩定性。基于SMC的ASR系統和路面自適應ASR系統都對車輛進行了行駛控制，基于SMC的ASR系統使車輛最大橫擺角速度減小至7 mrad/s，側向位移約為1.23 m.路面自適應ASR系統使車輛最大橫擺角速低于4 mrad/s，側向位移小于0.5 m.

4.2.3 對接路面行駛實驗

依照表3中的實驗工況3設置仿真條件，實驗結果如表6、圖22及圖23所示。

表6 對接路面估算誤差統計Tab.6 Estimation error statistics of docking road

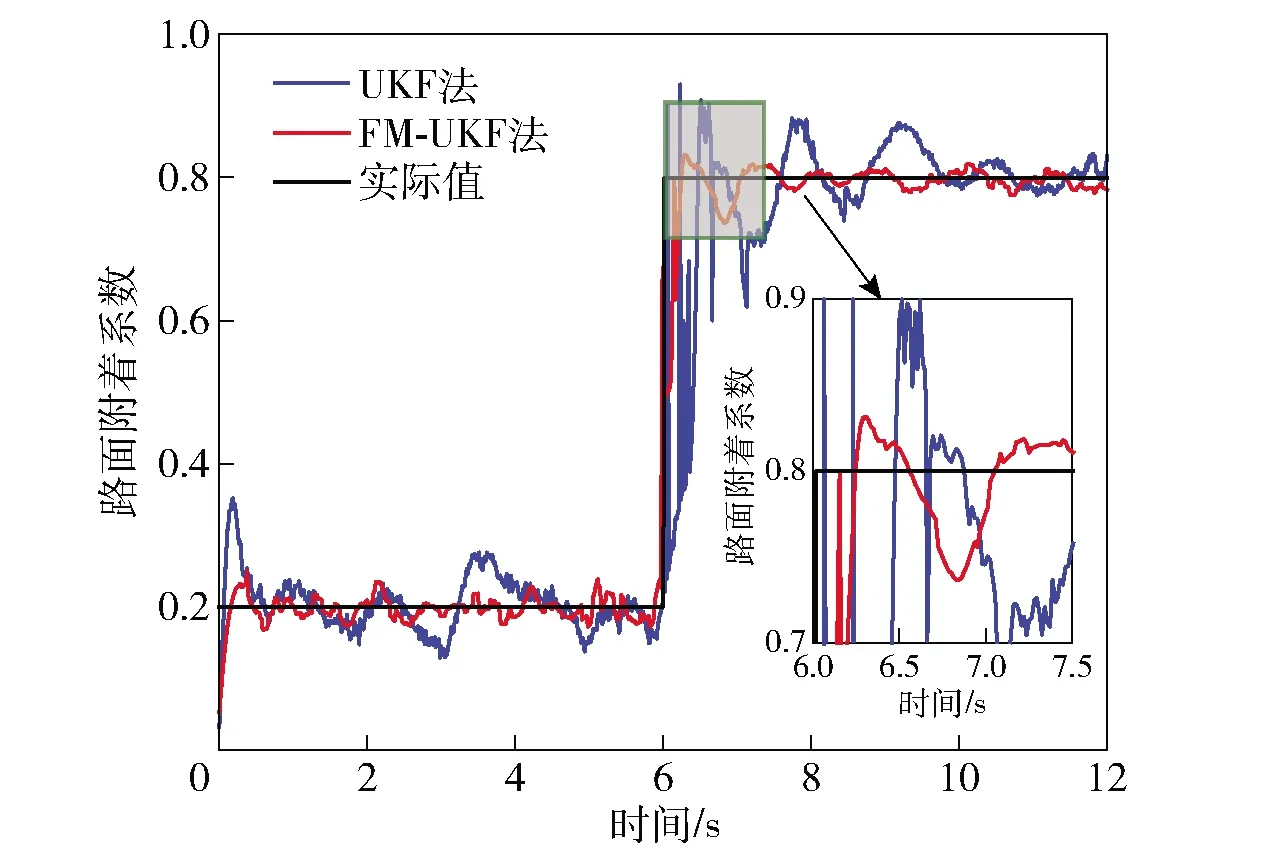
圖22 工況3的路面附著系數估算對比Fig.22 Road adhesion coefficient estimation under Condition 3

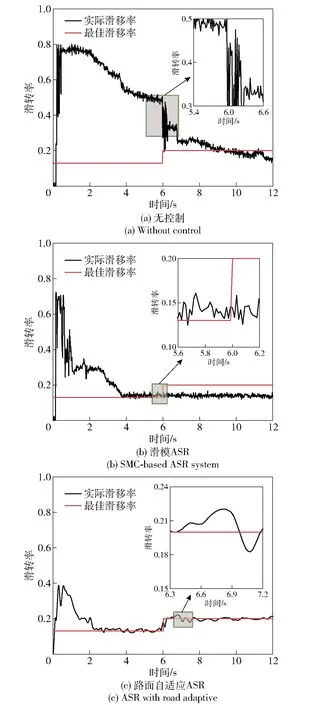
圖23 工況3的車輪滑轉率Fig.23 Slip ratio under Condition 3

表6及圖22結果表明，當行駛路況突然變化時，UKF法的路面附著系數估計值與實際值具有較大差異，而FM-UKF法的估計值依然非常準確地跟蹤實際值，這說明了FM-UKF法在對接路面上具有更好的估計效果。

從圖23(a)可以看出，在對接路面加速行駛時，未施加驅動力控制車輛驅動輪打滑現象非常明顯，實際滑轉率與最佳滑轉率的偏差很大，路面附著系數發生變化時，輪胎滑轉率出現明顯抖動，車輛動力性能和穩定性能較差。圖23(b)表明：滑模驅動防滑系統對改善驅動輪過度打滑現象具有一定的作用，減小了滑移率與最佳滑移率之間的差異，但系統無法識別道路突變，只能設定固定的最佳滑移率進行控制；此外，由于傳統滑模控制的特點，系統抖振現象明顯，影響了控制效果。圖23(c)表明，路面自適應ASR系統能夠快速感知路面附著系數的變化，并根據道路狀況及時調整最佳滑移率進行ASR，系統具有更小的抖動和更好的穩定性。

5 結論

本文針對多輪輪轂電機驅動車輛，進行車輛系統建模，采用FM-UKF法對行駛路面進行了辨識，實現路面附著系數的實時、準確估計。在路面識別的基礎上，實時確定當前道路最佳滑轉率，解決傳統ASR系統采用固定最佳滑轉率進行控制的問題，設計驅動力模糊滑模控制器，調整滑轉率與最佳滑轉率的偏差。基于dSPACE系統，進行了實時仿真實驗。得出以下主要結論：

1) FM-UKF法準確辨識了行駛路面的差異和躍變，響應迅速、魯棒性強。

2) 路面自適應ASR系統實現了路面自適應功能，具有較好地ASR效果：在低附著系數路面上，模糊滑模控制器迅速將實際滑轉率控制在最佳滑轉率間附近；在對開路面，依據左右側最佳滑轉率分別對兩側車輪施加驅動力控制，有效減小了滑轉率誤差；在對接路面，根據路面附著系數變化，對實際滑轉率進行了控制，較好地滿足了電驅動車輛在不同環境下的行駛需求。