一種小推力航天器變軌優化方法
遲進梓 余紅英 張子雄
中北大學,太原 030051
0 引言
目前,化學燃料推進和電推進是航天器的主要推力來源[1]。由于化學燃料推進方式比沖小,能量密度低,在執行任務時,攜帶大量推進劑,增加了衛星發射成本[2]。而電推進屬于小推力推進方式,由于其具有比沖大、控制精度高等特點,提高了探測器有效載荷的比重,具有優秀的研究應用前景[3]。電推進技術[4]是利用電力技術使推進劑膨脹,向后高速噴發,產生航天器所需推力的技術,適用于速度矢量較大以及保持軌道精度等變軌情況。
使衛星等航天器從原軌道轉移至期望軌道上,此過程稱之為軌道機動[5],本文針對小推力類軌道機動的軌道轉移問題進行研究。針對衛星等航天器模型的變軌問題,Kluever[6]提出了一種電推進軌道轉換權衡的算法,主要對化學-電混合推進的GEO軌道轉移方案進行研究,實現了快速開展大推力軌道變換。Fakoor等[7]將解析方法與基于種群的人工蜂群算法相結合,通過人工蜂群算法搜索控制變量的初值和目標函數的終止時間,給出了軌道轉移過程中狀態和控制變量的變化率,所得結果具有相當的收斂性和足夠的精度。Caillau等[8]對從GEO軌道到地月系L1點和月球軌道的航天器轉移軌道進行相關研究,雖然能實現航天器的軌道轉移,但此方法并未對小推力轉移軌道優化問題進行研究。付磊等[9]建立了多沖量變軌模型,得到最優沖量的時刻和大小,解決了遠程導引多沖量變軌問題。黎桪等[10]創造性地使用兩次偽譜法優化小推力軌道,較好克服一次偽譜法在求解燃料最優時產生的震蕩問題。Pontani等[11]聯合使用VTD-NOG和PD-RM控制完成了低推力月球軌道轉移。
本文提出一種新的軌道轉移和規劃算法,將小推力衛星變軌過程轉化為最優控制中兩點邊值問題,然后針對該問題引入混合遺傳算法進行解算,完成小推力航天器軌道轉移,實現了對小推力航天器由低軌向高軌的飛行軌道規劃和優化設計。
1 動力學模型
小推力航天器質量隨燃料消耗而減小,在飛行時主要受到發動機推力與地球重力作用,而春分點軌道根數與春分點坐標系OE-xyz相聯系,坐標系變換見文獻[2]。經過計算,以春分點軌道根數和衛星的燃料質量[r′,xh,yh,n1,n2,λ,m]為狀態量,不考慮攝動,改進春分點根數下的動力學模型為:
(1)
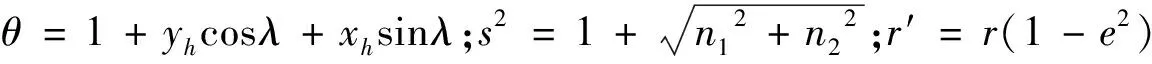
2 軌道轉移優化問題
軌道轉移優化是在已知航天器姿態以及初始狀態情形下,并在航天器滿足以春分點根數變分方程為基礎的航天器運動方程條件下,通過優化算法得到變軌過程中燃料消耗和時長的最優解。
2.1 小推力航天器運動方程
本文用春分點根數變分方程表示航天器的運動方程:
(2)
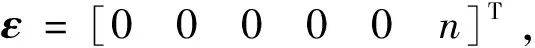
以k=[r,xh,yh,n1,n2,λ]T表示t時刻軌道狀態向量,k可表示為位置和速度的函數:
(3)
則有:
(4)
其中有:
(5)
P與m分別表示推力矢量與衛星的燃料質量,R為從地心到在軌服務對象的位置矢徑。式(4)中的春分點根數相對于位置和速度的偏導數通過春分點根數間的泊松括號與位置速度對于春分點根數的偏導數聯系起來,求得春分點軌跡根數矢量狀態變分表達式:
(6)
由式(6)可知,求出春分點根數關于速度的偏導數,代入式(5)得到最終的軌道根數變分方程。
2.2 最優控制問題描述
小推力變軌機動的軌跡優化,本質上是求燃料消耗最少且用時最短的軌跡。由于研究問題的背景不同,約束條件不同,導致最優控制問題不盡相同,需利用數值方法得解析解。本文選取的優化量是推力方向矢量。而目標函數分為燃料消耗以及時間消耗兩類。但如果變軌過程中持續推力一直為最大值,則兩類目標函數效果是一致的。根據飛行任務,目標衛星最終狀態要符合前期需求中的限定因素。在最短時間的約束條件下,其模型性能指標可表示為:
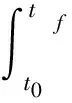
(7)
tf為最終時間,t0為初始時間。根據極大值原理以及式(1)中的燃料質量方程和式(2),哈密頓函數(H函數)為:
(8)
式(8)中,λxT為協態變量矩陣,λλ和λm為協態變量。由最優控制理論可知,若要達到最優控制目標,需使H函數可在某區間內取到極小值。而由式(8),航天器最佳推力方向應與矢量λxTN反向,即:
(9)
P應該滿足約束:
0≤P≤Pmax
(10)
P應該在這一區間內使H函數取到極小值,將H對P求偏導,得:
(11)
為H取極小值,選取合適點火開關函數[12]。協態方程為:
(12)
δ和η分別為推力的方位角和高低角,由δ和η確定推力方向角。協態變量在函數中還需要受到截斷因素的影響:
(13)
式(13)中,拉格朗日乘子用γ進行表示。由于tf自由,因此在最佳軌道時刻,哈密頓方程理應滿足以下表達:
H[k*(tf*),λ*(tf*),P*(tf*),tf*]=
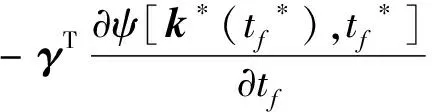
(14)
將式(8)、式(13)第二式代入式(14)可得:
(15)
式(7)~(13)一起組成最短時間約束條件下最佳目標參數函數方程組。本文求解該方程組思路是將狀態變量和協態變量轉化為兩點邊值問題,然后選用混合遺傳算法進行求解。
3 算法流程
遺傳算法具有較強的全局遍歷能力,使時間效率得到有效提高,但其局部查找能力不強,而經典優化算法恰好具有與之相反的特點。因此本文取兩者進行混合使用,使整個算法有良好的時間復雜度。
遺傳算法是一種通過分析系統整體特征,產生具有自我優化參數能力的算法模型。由于當前模型的特殊性,懲罰函數進行如式(16)定義:
(16)
p為整數,通常取1或2。βj是表示約束權重的因子。dj(Z)=0(j=1,2,…,n)表示等式約束。廣義適應度函數在懲罰函數約束下為:
F(Z)=J(Z)-φQ(Z)
(17)
式(17)中,φ為懲罰因子,當φ>0,φ→+∞時,原函數收斂得到最終結果。但因子系數較高或較低會導致結果與真實結果值相去甚遠,甚至破壞種群更迭條件。因此,本文使用具有自我調節能力退火篩選函數約束:T=T0,種群中懲罰因子為:
(18)
式(18)中,μ∈[0,1]表示溫度制冷速率常數;G代表種群繁衍層數,Tf是退火凝結溫度。式(16)中的βj選擇可以通過隨機權重的方法進行獲取:
(19)
式(19)中,lj是非負隨機數。
4 仿真實驗及結果
本章基于電推式小推力衛星軌道規劃的理論基礎,在開源科學工程計算軟件SCILAB6.0.1上的SiROS下開發了仿真模塊。并利用仿真模塊搭建了GTO-GEO軌道轉移仿真模型,對電推式小推力衛星變軌機動方案的優化算法進行驗證。
4.1 仿真模型搭建
本文4個仿真模塊是在SiROS下的宇航函數庫中開發的,分別是模塊1:初始軌道規劃模塊,模塊2:軌道優化模塊,模塊3:軌道動力學模塊,模塊4:變軌制導控制算法模塊。初始軌道規劃模塊封裝及連接如圖2所示。其是基于標稱軌道法設計的,輸出為小推力軌道優化結果,表示多圈小推力標稱軌道上各分段節點的軌道根數初值。
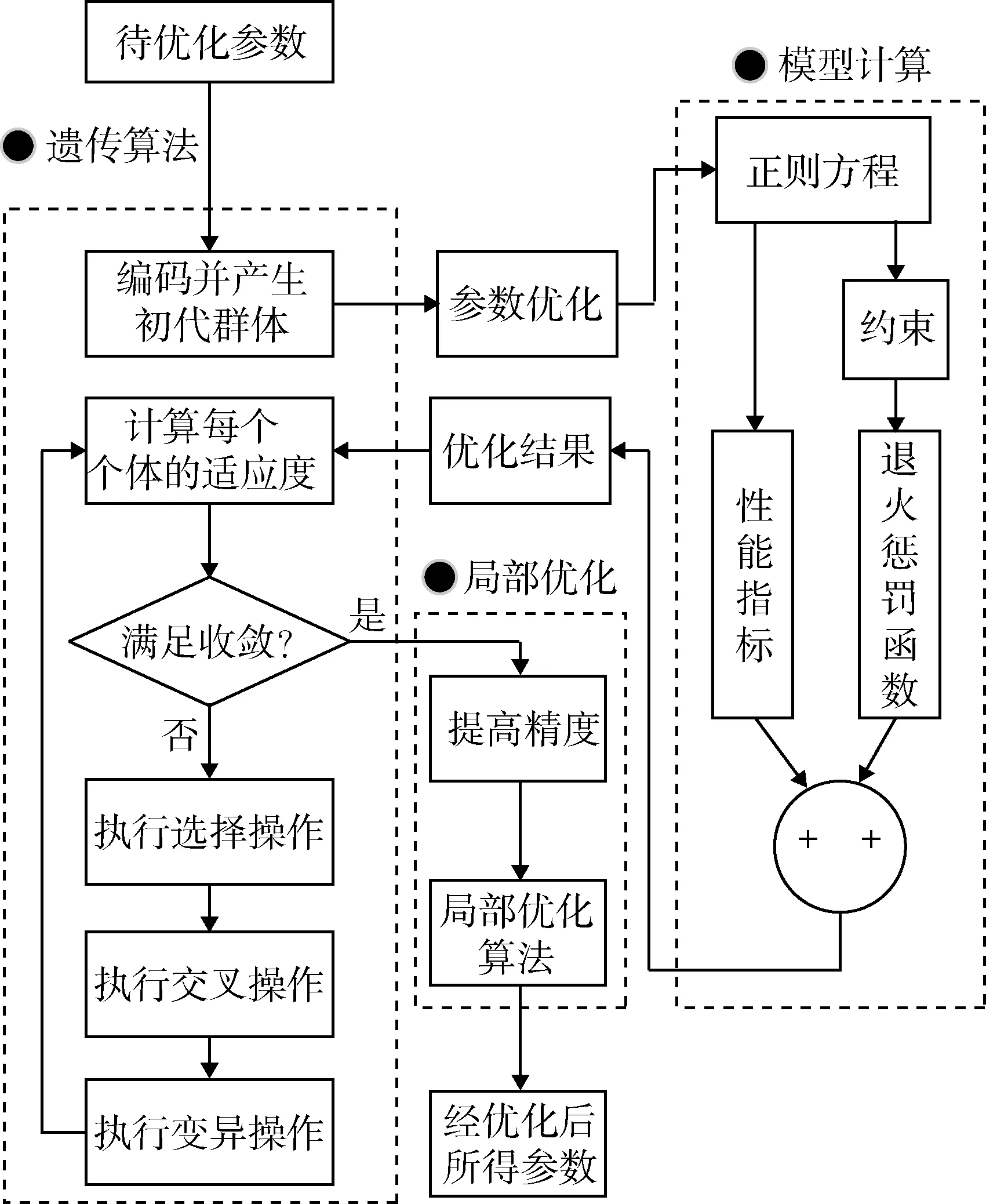
圖1 混合遺傳算法流程圖
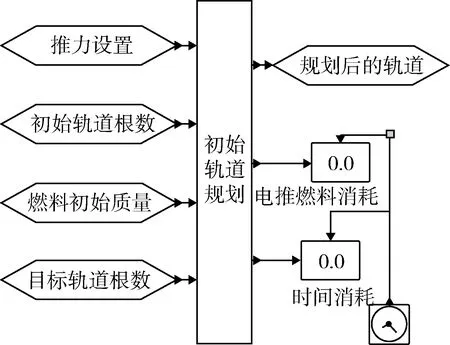
圖2 初始軌道規劃模塊封裝及連線
如圖3所示為軌道優化模塊封裝及連接圖,軌道優化設計模塊是根據本文優化方法開發的,給出基于退火遺傳算法得到的小推力軌道優化結果,其結果表示小推力軌道上各分段節點的軌道根數初值,參數值與初始標稱軌道規劃模塊一致。
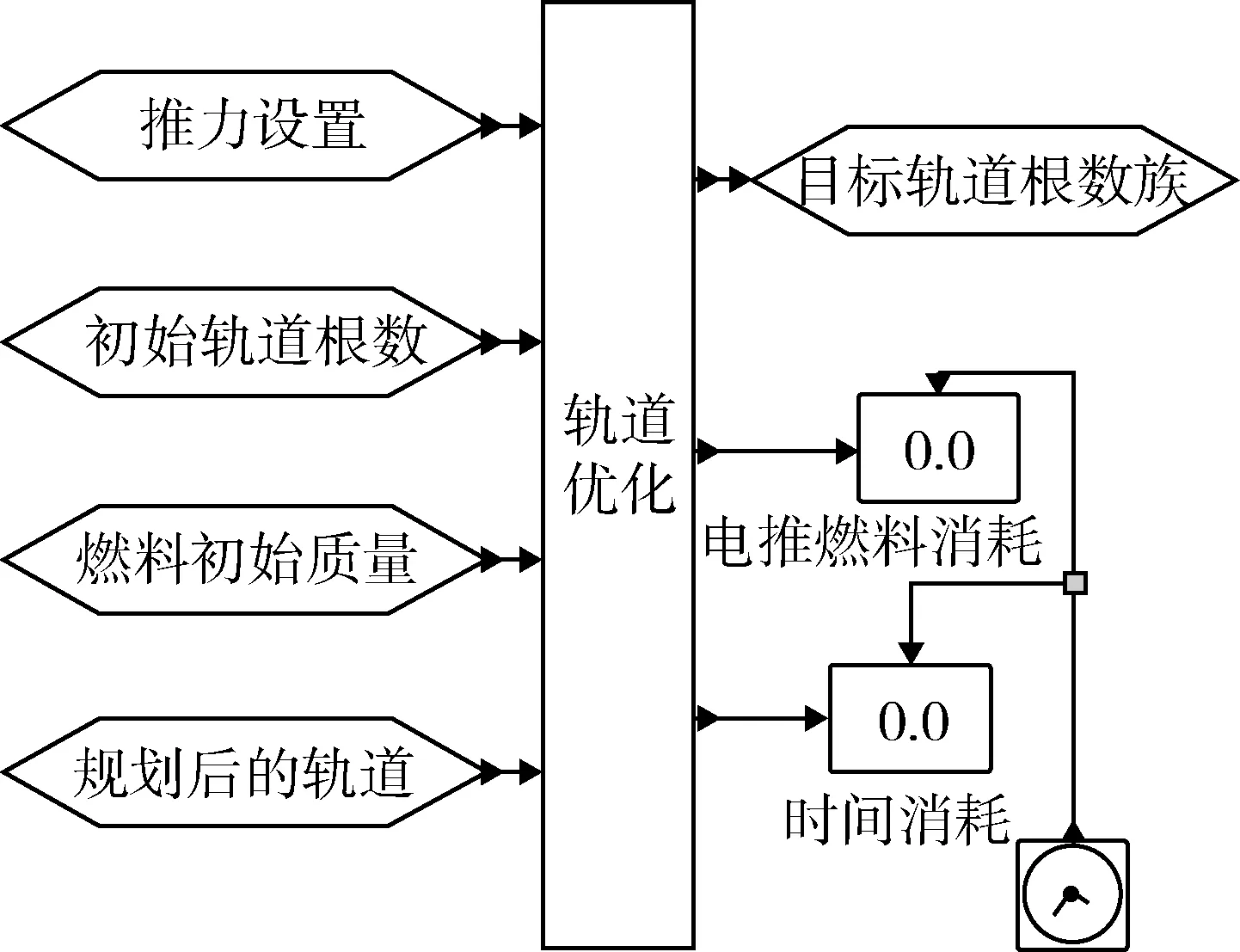
圖3 軌道優化模塊封裝及連線
如圖4所示為軌道動力模塊封裝及連接圖,將該模塊數據輸入模塊4,隨仿真時間的推進不斷計算新的軌道根數、飛行器質量、推力,直至仿真任務完成。該模塊的攝動加速度設置為常量。
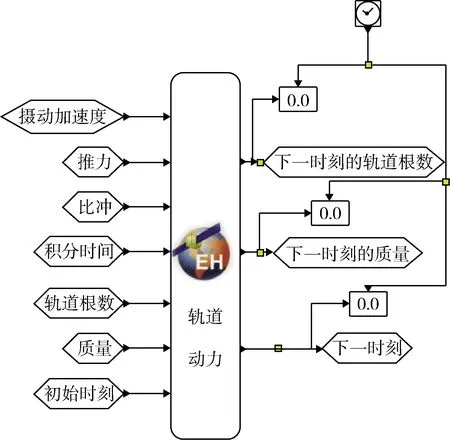
圖4 軌道動力模塊封裝及連線
而變軌制導控制模塊用來對規劃好的軌道進行跟蹤。變軌制導控制模塊封裝及連接如圖5所示。
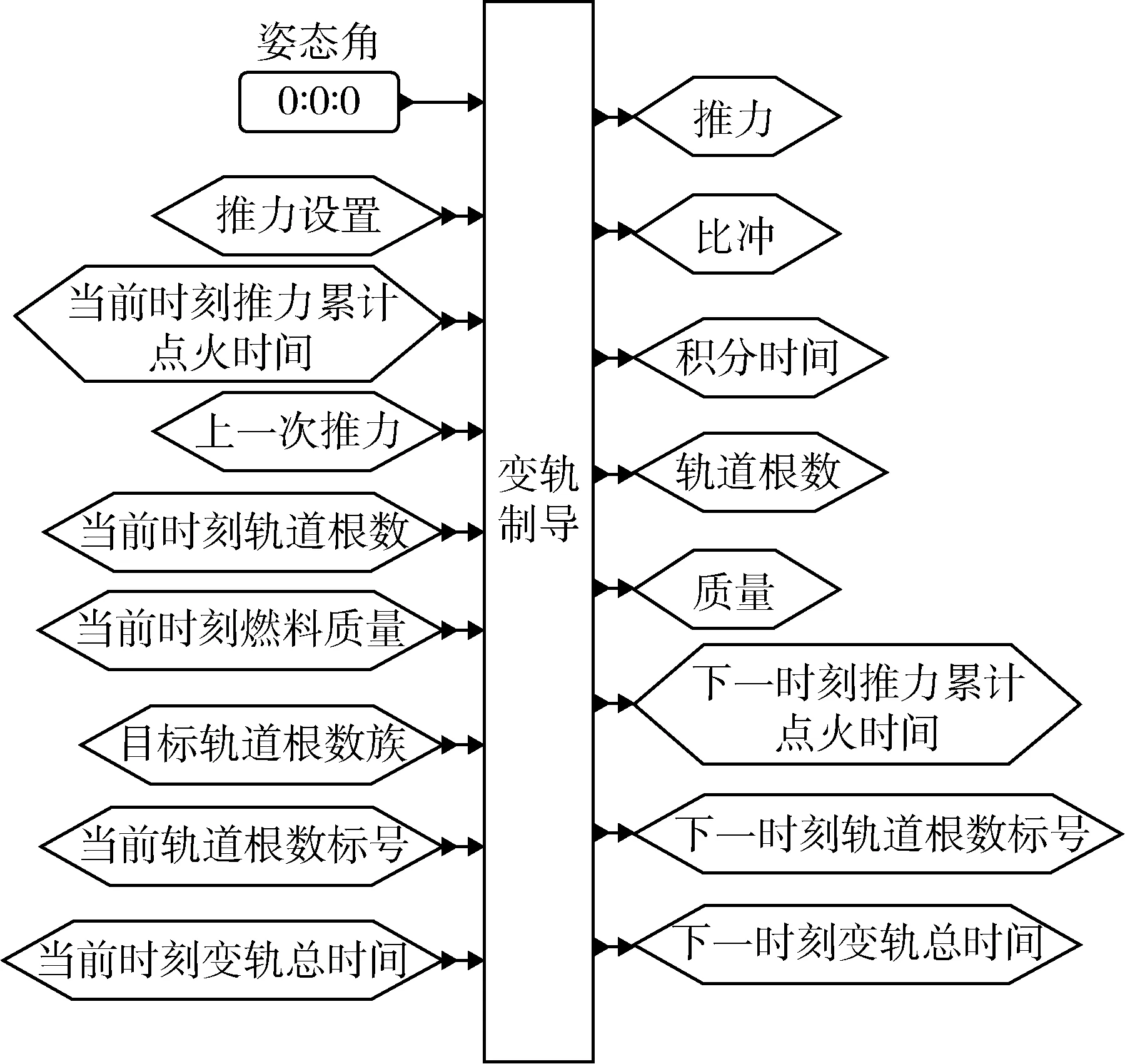
圖5 變軌制導模塊封裝及連線
各模塊需要配置參數如表1,輸出參數如表2。

表1 各模塊參數配置

表2 各模塊輸出參數
4.2 軌道轉移仿真與分析
變軌開始時間為2020年1月1日0時0分,初始質量為1500 kg,電推力比沖為3800,推力方位角上限為6.28 rad,推力上限為1 N。GTO-GEO軌道轉移仿真模型如圖6所示,各參數如表3所示。
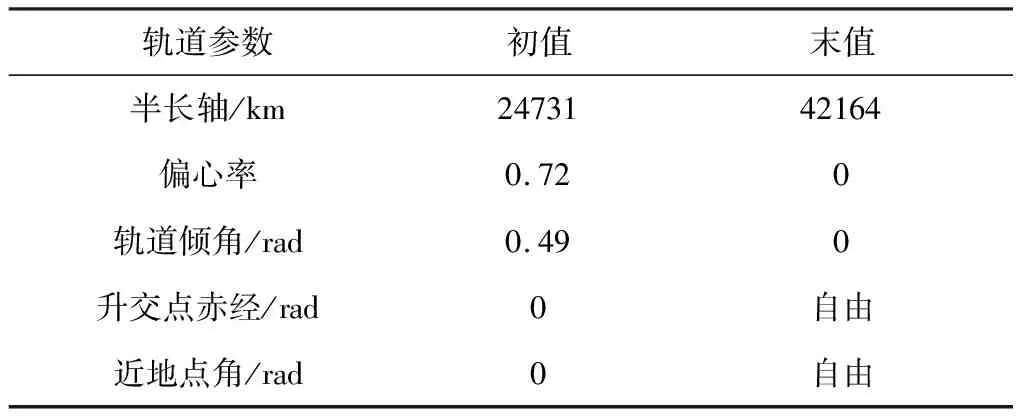
表3 模型各參數初值
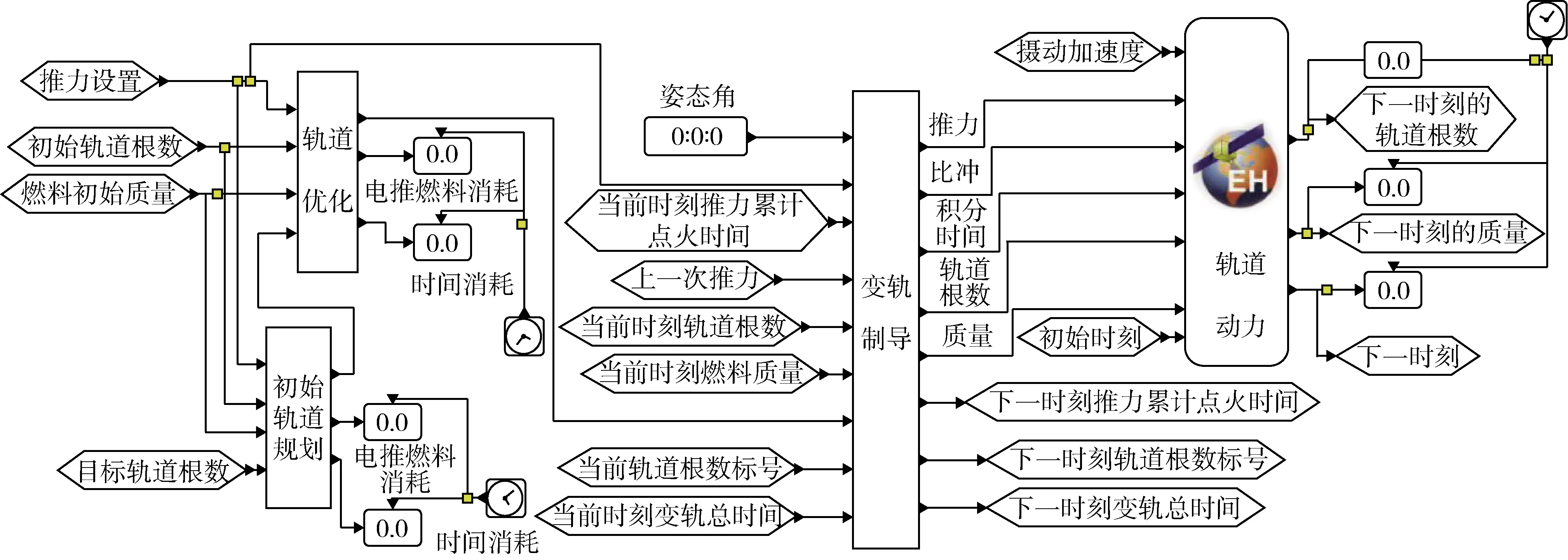
圖6 GTO-GEO軌道轉移仿真模型圖
為驗證該算法的正確性和有效性,將本文所提方法解與最優解進行性能比較。圖7為半長軸隨時間變化圖。圖8為偏心率矢量隨時間變化圖,圖9為傾角隨時間變化圖,圖10為推力隨時間變化圖。虛擬小推力飛行器模型在2020年01月01日00時00分出發,攜帶的初始燃料質量為1500 kg,在2020年02月 13日21時36分到達,所用的時間是44.9天,消耗燃料為171.2 kg。
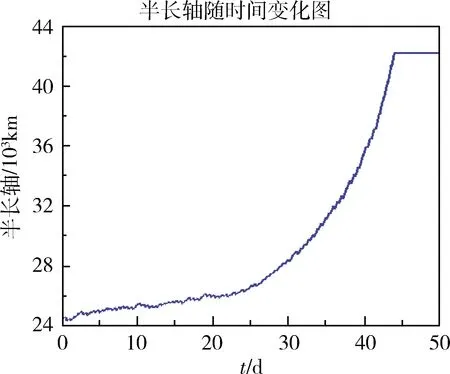
圖7 半長軸隨時間變化圖
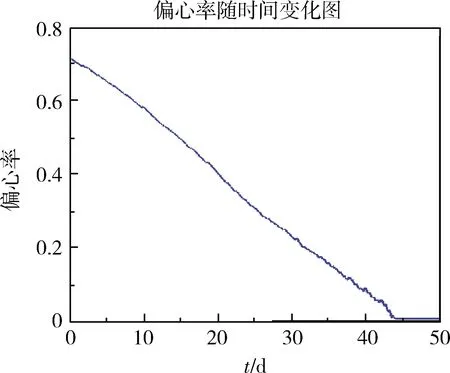
圖8 偏心率矢量隨時間變化圖
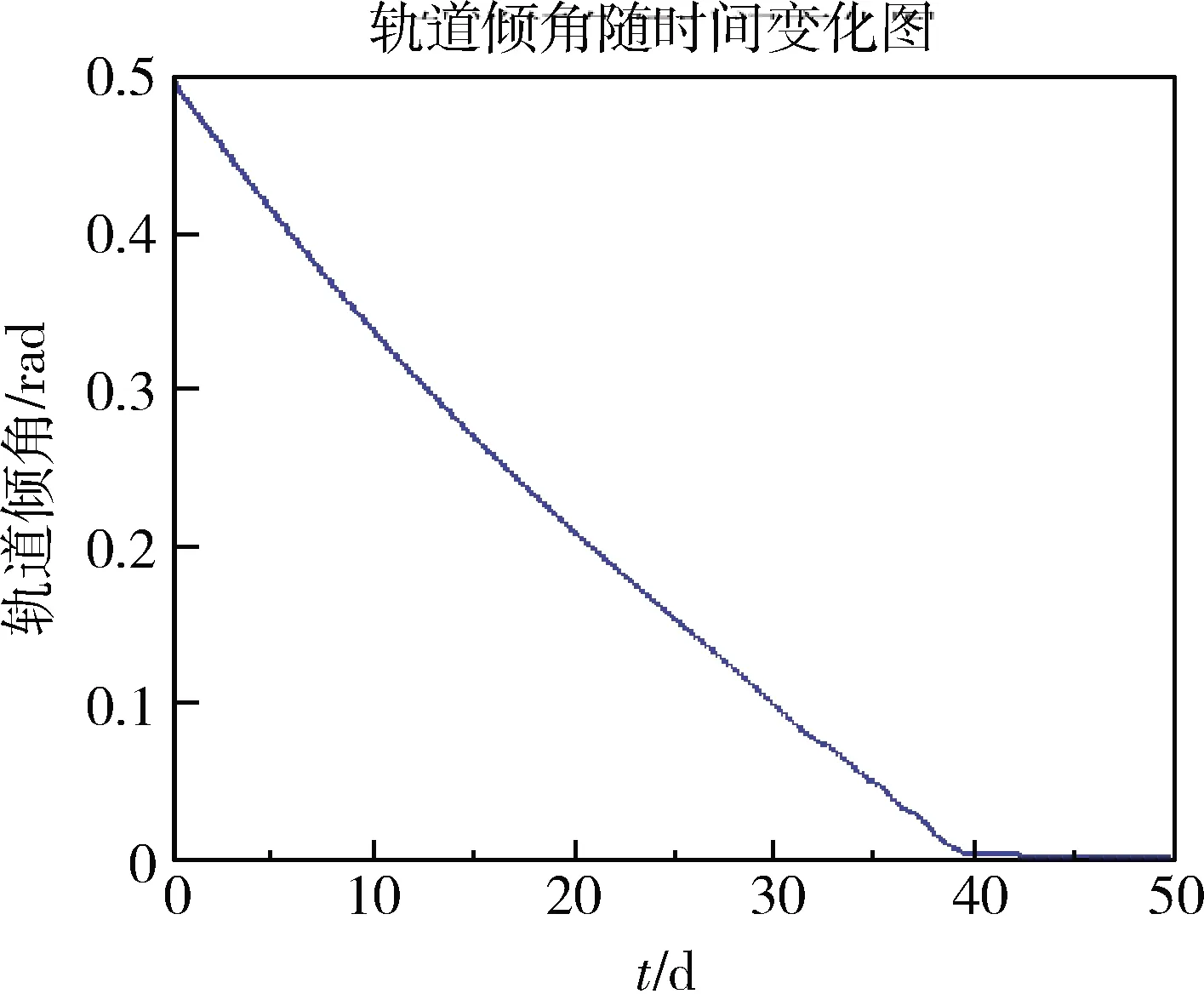
圖9 傾角隨時間變化圖
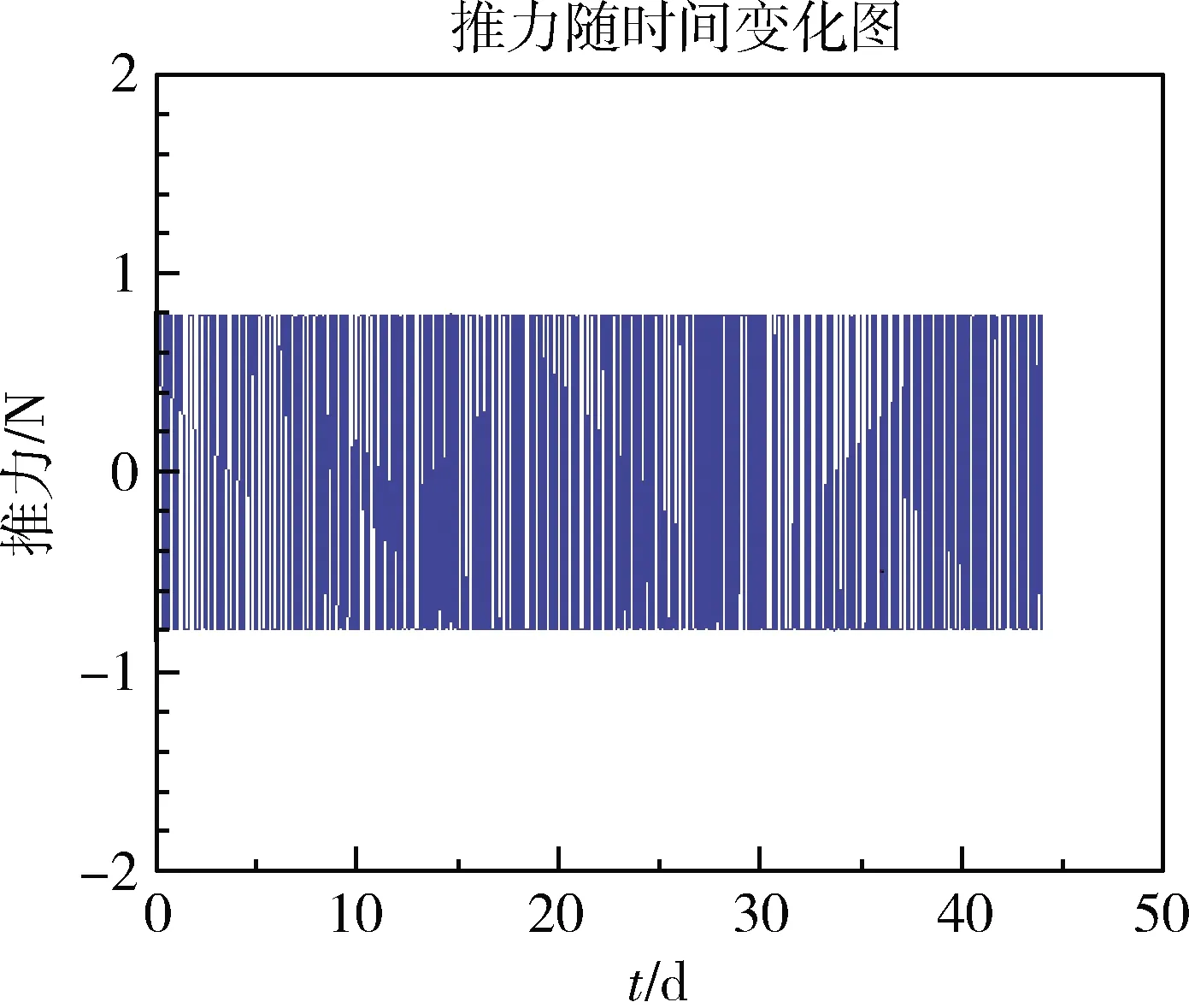
圖10 推力隨時間變化圖
圖11所示為推力示意圖,其中Ux,Uy和Uz分別為徑向、切向和法向小推力加速度,各推力分量變化如圖12~14所示,推力方位角變化如圖15~16所示。
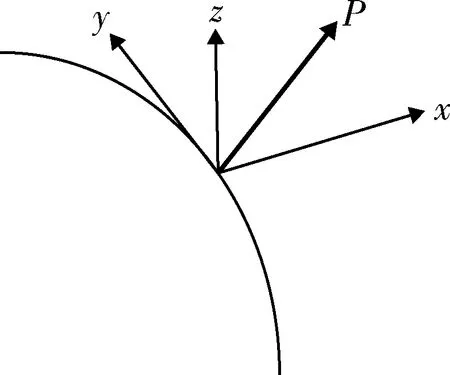
圖11 推力示意圖
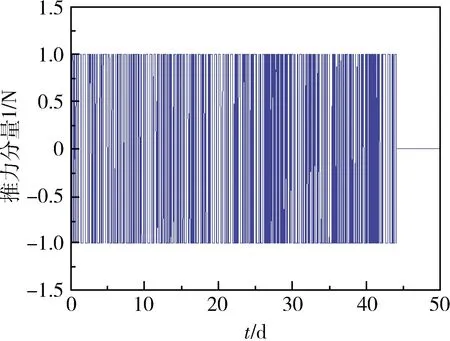
圖12 推力分量1示意圖
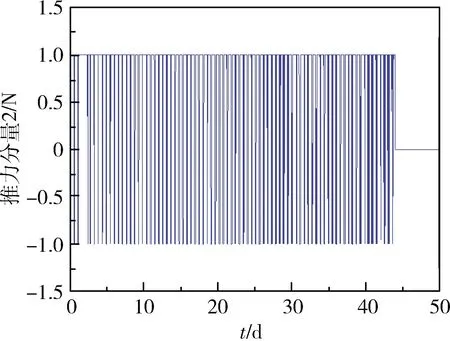
圖13 推力分量2示意圖
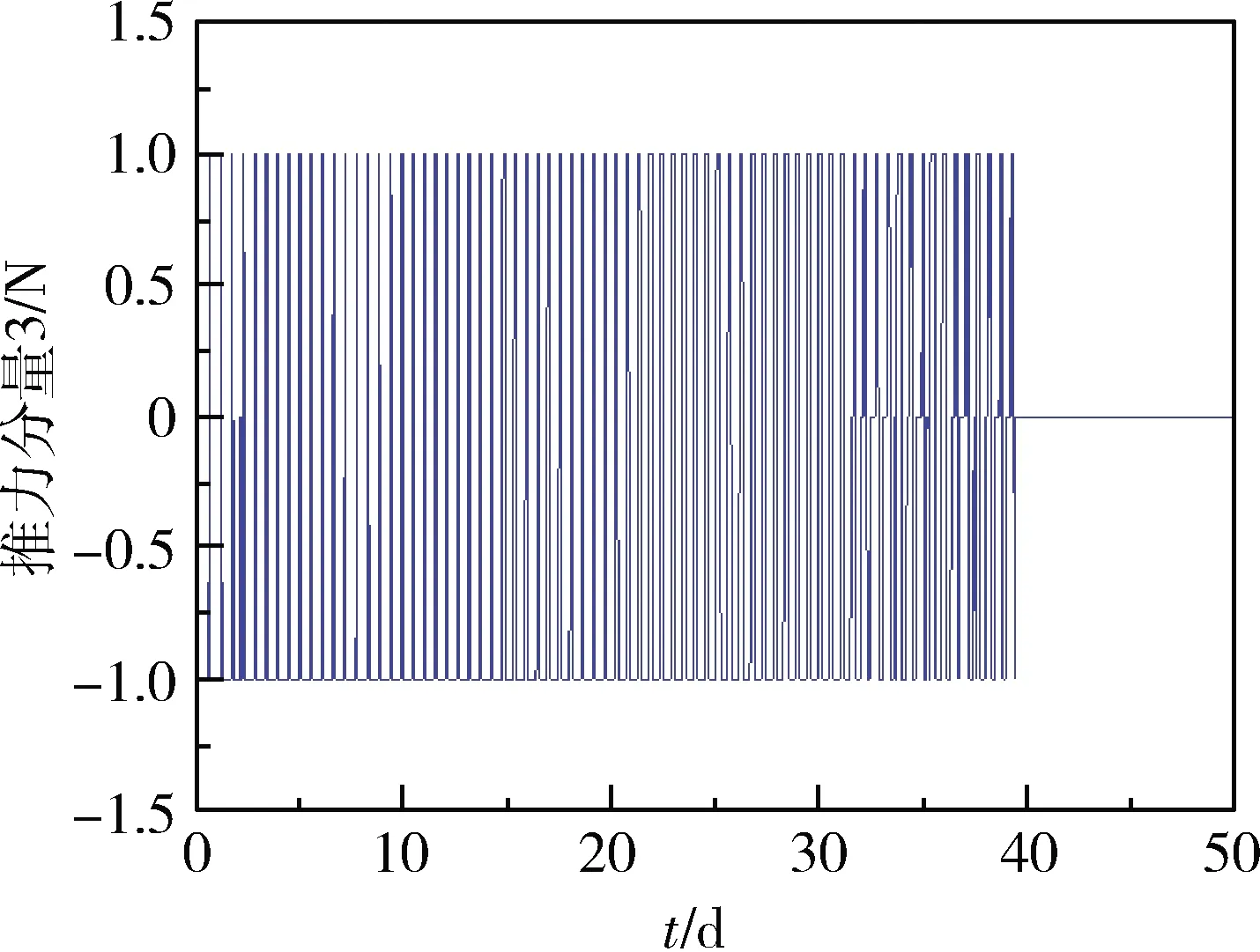
圖14 推力分量3示意圖
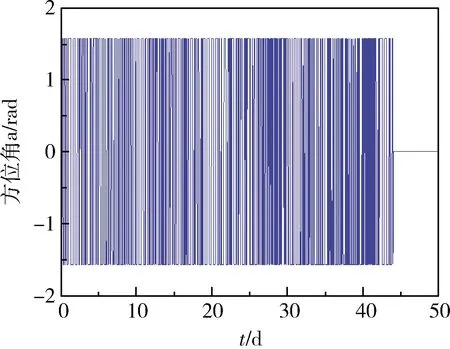
圖15 推力方位角1變化示意圖
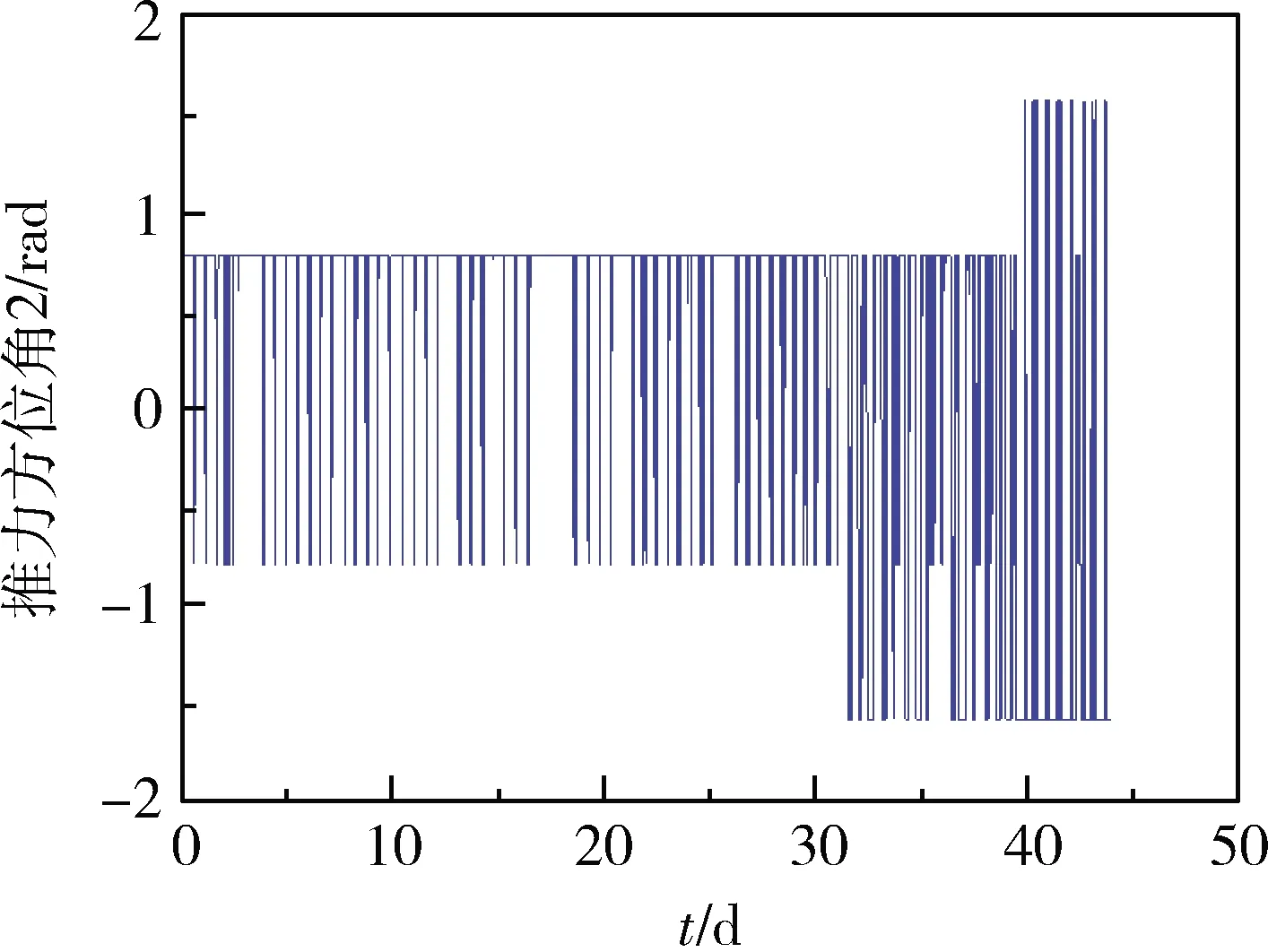
圖16 推力方位角2變化示意圖
在航天器由GTO軌道轉移到目標軌道時,由公式(1)可知,推力器產生的推力使軌道半長軸增大,軌道偏心率降低,軌道傾角減小。由圖7~10可知,在小推力航天器進行軌道變換期間,偏心率矢量與軌道傾角單調下降,而半長軸單調上升,推力的方向和大小都成周期性變化,與理論分析相符。推力方位角1在[-45°,45°]范圍內變化,推力方位角2在[-90°,90°]范圍內變化,直至變軌結束。通過對GTO-GEO軌道轉移的過程進行仿真與分析,可以得到仿真結果如表4所示。
其中,最優解結果是不考慮對軌道產生顯著影響的攝動因素的結果,混合動力是本算法下化學燃料和電推進混合推進方式。由表4可知,本文所提算法消耗了占總質量的11.4%的燃料,在燃料消耗上,僅比最優解多1.2%,而相較于傳統遺傳算法,本文算法節省了3.7%的燃料,相較于混合動力模型,本文算法節省了10.7%的燃料。本文所提算法完成變軌用時44.9天,時間消耗上,僅比最優解多13.9%,而相較于傳統遺傳算法,本文算法節省了30.9%的時間,相較于混合動力模型,本文算法節省了19.8%的時間。由此可見,本文所提算法能順利完成GTO軌道至GEO軌道的轉移任務,各模塊運行正常,能以接近于最優控制解的結論完成變軌,輸出預期的結果值,具有燃料消耗次優的特點,降低了發射成本。
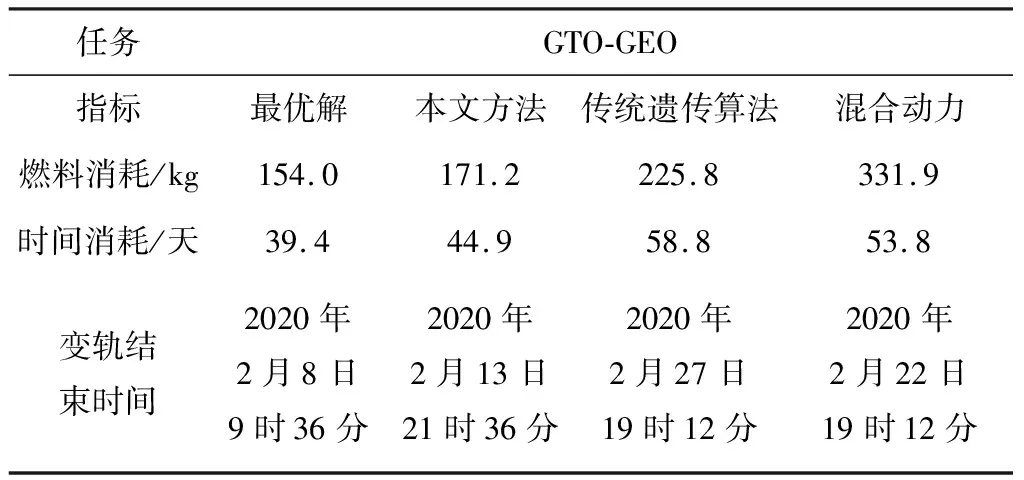
表4 GTO-GEO變軌燃料和時間消耗
5 結論
在連續小推力衛星變軌以及制導控制過程中,本文將電推進式小推力衛星模型的變軌過程轉化為最優控制中兩點邊值問題,然后針對該問題使用混合遺傳算法進行解算。在SCILAB6.0.1上進行實驗,驗證了本文提出的小推力衛星變軌算法優化設計方法。實驗結果表明,變軌實際消耗燃料較最優解僅多1.2%,消耗時間較最優解僅多13.9%,且相較于傳統遺傳算法以及傳統動力模型,燃料和時間消耗都大大減少,完成了小推力航天器由低軌向高軌的飛行軌道規劃及優化。

