考慮時間約束的多飛行器軌跡優化方法研究

楊卓喬 呂春紅

1.北京航天自動控制研究所，北京 100854 2.宇航智能控制技術國家級重點研究室，北京 100854

0 引言

隨著飛行器所要承擔和執行的任務越來越具體，面對的場景越來越復雜，多枚飛行器同時實現同一任務目標的需求越來越受到各方的關注。而從同一發射場對多枚飛行器進行集群發射，不僅有著易于維護和管理的優勢，也可以更好地在惡劣的環境下實現任務目標。

對于集群發射的飛行器，發射時間是一項非常關鍵的因素，為了提升任務效果，通常要求發射持續時間或者到達目標的間隔時間盡量短，同時在設計發射時間的時候又存在著發射時間段約束，發射安全時間間隔約束[1]等眾多約束。為了更好地滿足這些條件，提升集群發射的效果，則需要對飛行器的飛行時間在發射前預先進行規劃。這本質上是一個飛行器軌跡的設計與優化問題。

軌跡優化是指在特定的約束條件下，尋找飛行器從初始點到目標點滿足某種性能指標最優的運動軌跡。在實際工程中一般將軌跡優化問題轉化為參數優化，利用非線性規劃的方法進行解算。文獻[2]采用改進遺傳算法，提出了一種落點散布最小的優化飛行程序方法。文獻[3]通過構建基于徑向基函數的神經網絡來模擬彈道模型，優化了導彈的最大射程。文獻[4]利用改進的Gauss偽譜法，解決了有繞飛區域的再入軌跡優化問題。文獻[5]采用序列二次規劃方法，進行了最大運載能力的彈道優化。文獻[6]采用序列凸優化的方法，提升了飛行器的機動繞飛能力。

目前雖然軌跡優化的方法已經有許多比較成熟的方法，但國內外鮮有以飛行器飛行總時間為目標進行優化的研究。本文以存在發射安全時間間隔的同一發射場進行集群發射的多枚飛行器為背景，采用序列二次規劃法(SQP)，以飛行器飛行總時長為目標來進行飛行器軌跡的設計與優化，得到滿足安全時間間隔和最短到達時間間隔的多飛行器軌跡優化方案。

1 飛行器主動段模型

飛行器的主動段為飛行器的有動力飛行，即發動機連續工作的時間段。飛行器主動段終點參數一旦確定，飛行器的軌跡基本就可以固定，所以飛行器的軌跡優化主要是設計主動段程序角。

1.1 飛行動力學模型

考慮地球為旋轉橢球，采用標準大氣模型，作用于飛行器上的力主要包括發動機推力、重力和氣動力。在發射慣性系內建立飛行器質心運動方程[7]。

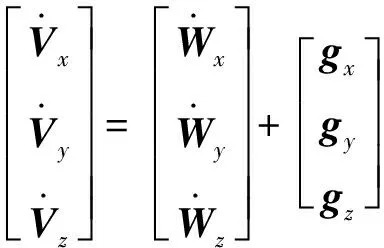
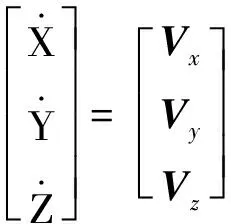
(1)

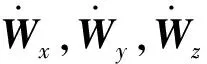
其中視加速度按式(2)計算：

(2)

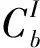
1.2 主動段程序角設計模型

飛行器軌跡設計就是對主動段的標準程序角進行設計，在滿足約束條件的情況下實現設計的目標。一般情況下，在軌跡規劃時可以不考慮飛行器側向的偏航與滾轉程序，即令這兩個角為0，大部分研究都集中在主動段俯仰程序角的設計上。

考慮將飛行程序分為大氣層內飛行段與真空飛行段，大氣層內飛行段又可以分為垂直上升段，亞音速轉彎段和彈道轉彎段[8]。

俯仰程序角的模型可以總結為：

(3)

式中：θ(t)為軌道傾角，而α(t)為程序轉彎攻角，φcx0為t3時刻俯仰程序角的值。其模型可取為：

α(t)=4αmea(t1-t)(ea(t1-1)-1)

(4)

該經驗公式中：αm為該段攻角絕對值的最大值，a為常系數，其值大小影響攻角趨向于0的速度。

由于亞音速轉彎段的結束時間和真空飛行段的開始時間是確定的，可以得出，俯仰角由以下參數決定：

(5)

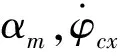
2 主動段軌跡優化模型

本文旨在研究，通過主動段軌跡優化，滿足給定固定射程的同時，使飛行器總的飛行時間與目標時間相差最小。同時滿足飛行軌跡的過程及終端約束條件。根據問題建立飛行器主動段軌跡優化模型。

2.1 性能指標

本文研究的主要優化目標包含射程和飛行時間2個方面，需要同時滿足射程和時間的要求，是一個多目標優化的問題，這2個分目標的函數分別為[9]：

(6)

式中：J1表示飛行器的實際飛行總時間相對目標時間的偏差絕對值最小；J2表示飛行器的實際射程相對目標射程偏差絕對值最小。

引入“權系數”，a1,a2對其進行調整，可以將多目標優化問題轉化成單目標優化問題進行分析，獲得唯一的一個優化性能指標，如式(7)所示。

(7)

2.2 優化參數約束

由于飛行器結構約束和飛行軌跡約束等要求，在優化參數的同時需要對過程參數進行限制，具體如下：

3)為了給飛行器后續有足夠的時間進行軌跡修正，要求真空飛行段時間:0s≤t4-t3≤25s；

4)攻角約束：αmin≤α≤αmax；

2.3 優化變量

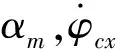
(8)

3 序列二次規劃算法(SQP)求解方法

本文將飛行器的主動段優化設計轉化為參數優化問題，設置主動段程序角特征參數作為優化變量，并通過非線性規劃的理論與方法求解。目前對于這類非線性規劃問題的求解方法已經發展的非常成熟，例如單純形法、共軛梯度法、擬牛頓法以及SQP算法都是有效的工具。SQP算法包含了所求解問題的二階導數信息，所以在擁有全局收斂性的同時，在局部可以實現超1次的收斂性，是目前求解光滑的非線性規劃問題所廣泛使用的算法之一[10-11]。

其基本原理就是在給定的近似點處通過二次近似逐漸得到一個更好的迭代點，這需要通過求解二次規劃子問題得到。在當前迭代點處進行一系列二次規劃子問題的求解，使得迭代點逐漸接近原優化問題的最優點，最后收斂至最優解，令我們所要解決的飛行器軌跡非線性規劃問題為P，其簡要計算步驟如下[12]：

2)求解二次規劃子問題的表達式：

(9)

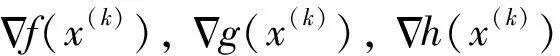
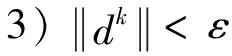
4)一維搜索：轉化為一維最優化問題minP(xk+λdk,r)，求出最優步長λ(k)，令x(k+1)=x(k)+λd(k)

5)更新矩陣H(k)：用BFGS公式更新矩陣H(k)確定新的正定對稱矩陣H(k+1)，令k=k+1返回第2步。

根據上一節建立的飛行器軌跡優化模型，采用SQP算法，對其進行優化設計和仿真，其計算流程如圖1所示。

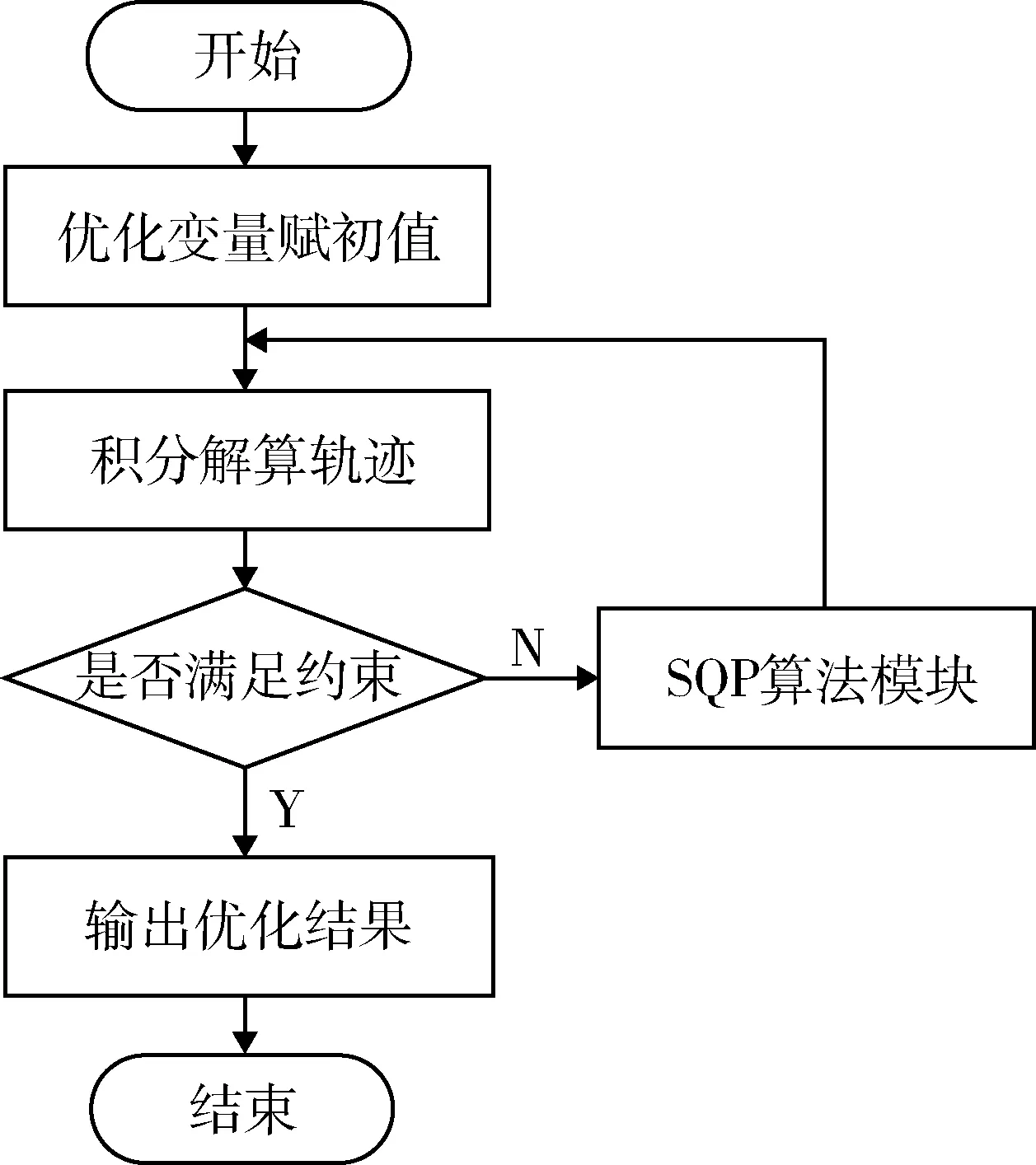
圖1 SQP算法軌跡優化流程圖

4 基于RBF神經網絡的模型計算

在飛行器軌跡的設計和上一章的優化中，需要多次對飛行器動力學模型積分求解，得到飛行器軌跡。采用傳統龍格庫塔等數值積分方法，計算量大，且1條軌跡的計算時間較長，為了提高計算效率，在優化參數前，先擬合軌跡模型。本文采用徑向基函數(Radial Basis Function，RBF)方法對飛行器模型進行擬合。

徑向基函數是用于多變量函數插值的一種傳統方法。與其他類型的人工神經網絡相比，RBF神經網絡具有深厚的生理學基礎，其簡單的網絡結構、快速的學習能力和優良的逼近性能，已在許多領域得到廣泛應用[13]。

RBF神經網絡是一種三層前向神經網絡，輸入層由一些感知單元組成，不對信號做任何處理，傳遞信號到隱層；隱層采用徑向基函數作為激活函數，通常具有較多的神經元個數，完成從輸入空間到隱層空間的非線性變換；輸出層對隱層輸出進行線性組合，從而對輸入信號做出響應。RBF網絡的一大顯著特點是隱節點的基函數采用高斯函數、多二次函數、薄板樣條函數等形式的距離函數。本文所選取的基函數為高斯函數，其形式如式(10)：

(10)

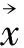
本文將RBF神經網絡的輸入層設置為飛行器軌跡積分模型的輸入，輸出則為射程和時間這2個重要的性能指標，所使用的RBF網絡結構如圖2所示，是具有2個輸入，多個隱層神經元及2個輸出的三層RBF神經網絡結構。

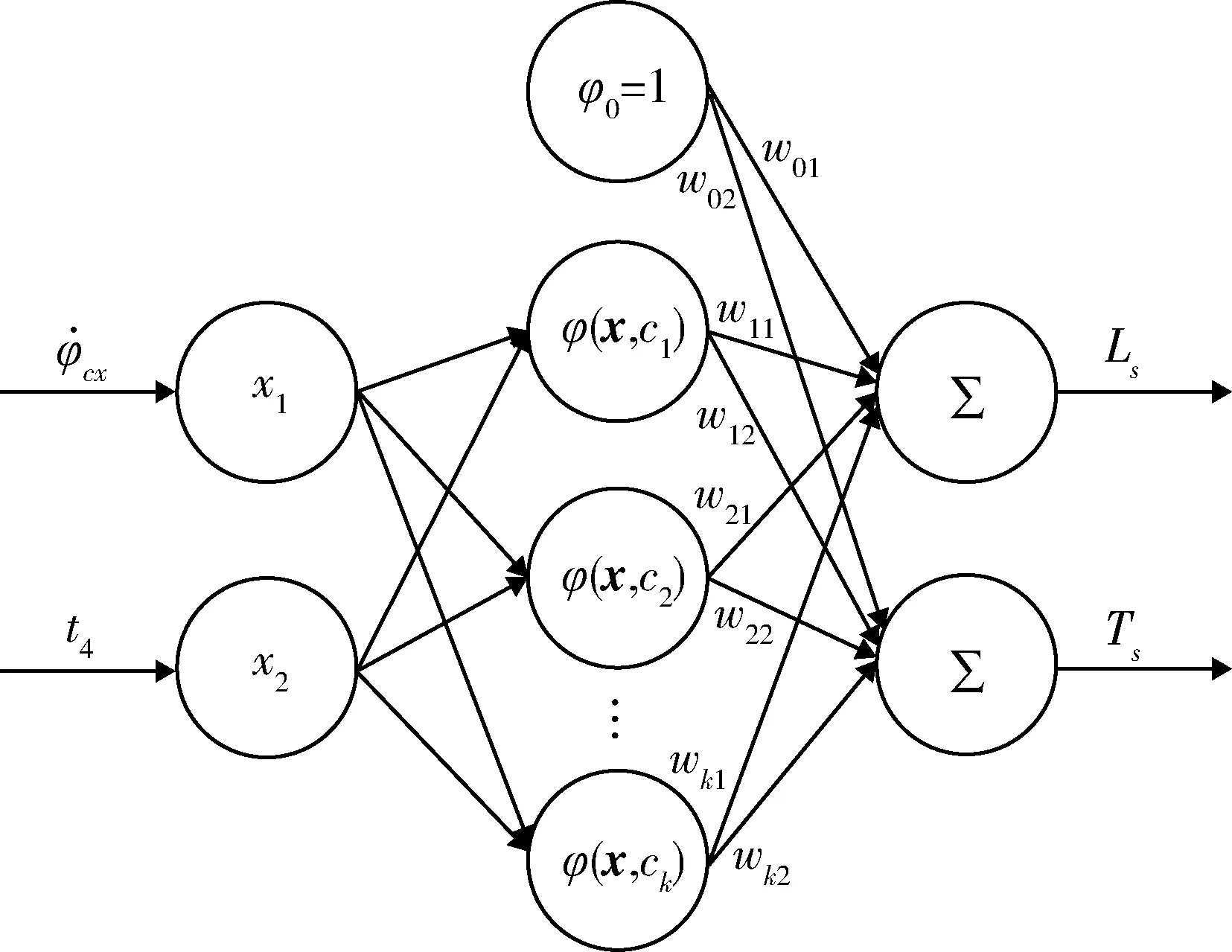
圖2 基于RBF神經網絡的飛行器軌跡參數計算模型

根據圖2構建的基于RBF神經網絡的飛行器軌跡參數計算模型，進行適當的學習訓練，即可代替圖1中的“積分解算軌跡”模塊，提升運算速度。

5 仿真校驗

5.1 飛行器軌跡參數計算模型的擬合與校驗

以某軸對稱式飛行器為例，仿真驗證本文的軌跡優化方法。首先根據式(1)～(2)以及飛行器模型參數，對飛行器軌跡積分模型進行建模。再通過SQP方法，僅以射程為目標，設計出1條性能較好的標準軌跡。依據此條標準軌跡所使用的參數，選擇合適的區間進行RBF網絡的設計。

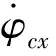
從樣本數據集中提取1900組數據作為訓練樣本，余下100組作為測試樣本，用于檢驗神經網絡計算精度。在對樣本進行標準化處理后，選取合理的初始參數，確定目標誤差，并對網絡進行訓練，最后用測試樣本對徑向基網絡估算出的射程和飛行時間偏差進行檢驗，兩者的檢驗結果如圖3～4所示，射程的平均相對誤差約為1.93*10-5%，時間的平均相對誤差約為1.73*10-5%。所得精度符合要求，即將所得網絡代入到后續的SQP優化流程之中。

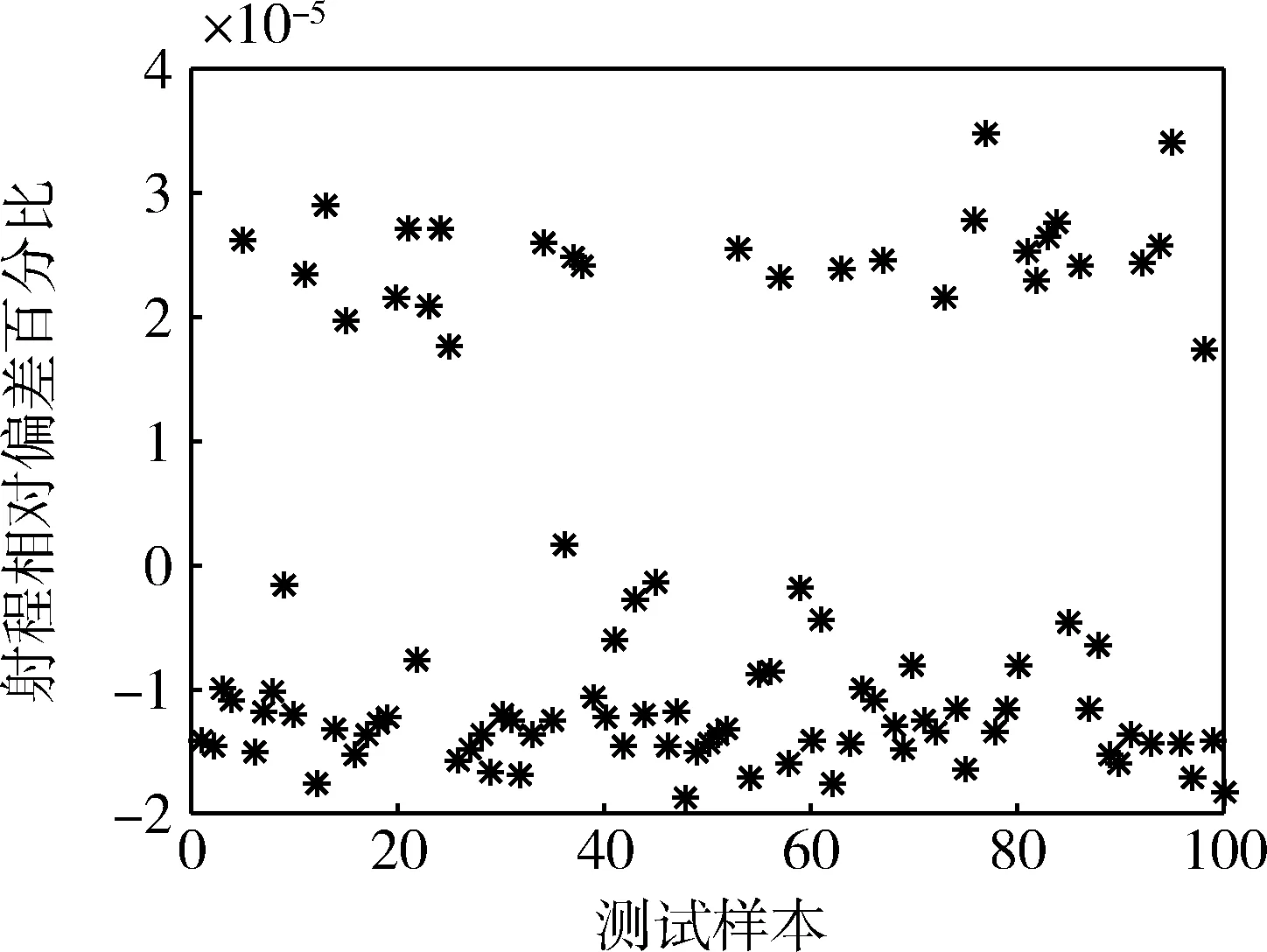
圖3 RBF神經網絡測試樣本射程相對偏差

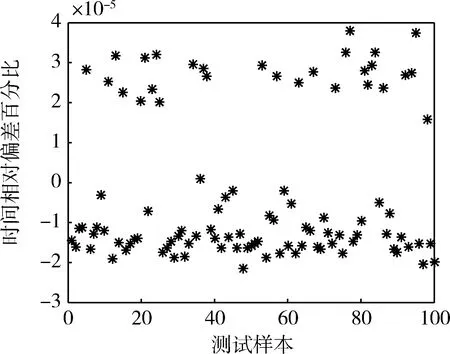
圖4 RBF神經網絡測試樣本飛行時間相對偏差

5.2 多飛行器軌跡優化

在考慮多枚同一發射場集群發射的多枚飛行器完成同一任務時，既要考慮發射時的安全時間間隔的要求，又要使到達時間間隔盡可能最短，這就需要我們對于同一發射點和目標點的飛行器設計多條不同的軌跡，并且令這些軌跡有著不同的飛行時間和相同的射程。

假設發射時的安全時間間隔為5s，那么第n枚發射的飛行器的飛行總時長就需要盡可能的比第1枚的減少5ns。根據5.1節，將僅以射程為目標所設計出的標準軌跡為第1枚飛行器所使用，總共對同一目標發射4枚飛行器。以每枚飛行器的時間和射程為優化目標，以上面得到的標準軌跡中的參數作為優化變量的初值，利用第2章所建立的優化模型，“權系數”a1,a2設置為1、1800，采用SQP方法進行優化，可以得到結果如表1。

表1中的優化結果1～3分別為第2枚至第4枚發射的飛行器所設計的飛行軌跡，表中給出了其飛行總時間和射程相對于標準軌跡的偏差。根據前文所設定的安全時間間隔飛行器將以5s的間隔發射，可以看出每枚飛行器的飛行時間的偏差都與其和第1枚飛行器的發射間隔相近，而射程的偏差不大，符合多飛行器同時到達的任務要求。如果多枚飛行器都采用傳統設計方法設計軌跡的話，每枚飛行器的總用時是相同的，因為每枚發射之間有5s的間隔，假設各飛行器的結構、發動機、質量等參數相同，則在不進行軌跡優化的情況下，4枚飛行器到達目標點的最長時間間隔約為15s。而采用本文方法，針對第2～4枚飛行器軌跡進行優化，使得其與第1枚飛行器盡可能同時到達目標點。采用SQP方法進行優化后，通過仿真結果可以看出，4枚飛行器到達目標點的最大時間差約為0.182s左右，實現了同時到達目標點的需求，可以看出本文研究的方法可大幅提升飛行器的任務效果。

表1 多枚飛行器的優化結果

6 結論

考慮多枚飛行器集群發射的需求，采用了飛行總時間和射程作為優化目標，選取了飛行過程中易于調整、且有著關鍵作用的參數作為優化變量，建立了飛行器俯仰程序角的優化模型。采用RBF神經網絡對飛行器軌跡參數計算模型進行擬合，利用SQP算法對多枚彈道進行了彈道的優化與仿真計算，同時保證了優化計算的效率與精度。

結果表明，該方法在保證了同一發射場部署的多枚飛行器發射的安全性的同時，大幅降低了其到達任務目標點的時間間隔，保證了多枚飛行器在時間和空間上的一致性，對于集群發射的飛行器共同執行同一任務有著較大的意義。