關于管端瞬態流的結構動力分析研究
劉浪
1.核電安全監控技術與裝備國家重點實驗室,廣東 深圳 518172 2.深圳中廣核工程設計有限公司,廣東 深圳 518172
根據ANS58.2-1988[1]和EJ/T335-1998[2],壓水堆核電廠的管道應考慮假想管道破裂。因為管道內的壓力遠大于環境壓力,所以管道內的流體介質從破口處高速噴放至環境中形成巨大的噴射流,一方面噴射流對管道的反推作用力巨大引起管道甩動效應;另一方面噴射流對墻壁、設備等造成噴射沖擊效應;同時管道因破口噴射急劇泄壓,管道內部產生壓力波(稱為瞬態流),該瞬態流作用在管道彎頭位置,會造成管道系統破壞。針對上述3 種動態效應(甩擊、噴射、瞬態流),需要為管道系統提供相關的防護設計,以保證管道發生破裂后,相關系統完整性沒有喪失,仍能執行核安全功能[3]。
開展管道完整性分析的前提是對瞬態流載荷進行詳細計算,然而該計算非常復雜耗時。該載荷是時間和空間的函數,取決于破口位置、破口打開時間、破口流通面積、破口發生前管道內的流體狀態、摩擦損失、管道所在的系統特性、管道的幾何特征及其他因素,水力學模型十分復雜[4?5]。ANS58.2 附錄B 提供了一種關于計算管端瞬態流的簡化方法,管端瞬態流是指管道破口附近第1 個彎頭處的瞬態流,其載荷峰值較其他管道彎頭處的瞬態流大很多,ANS58.2 中簡單地取載荷數值最大值認為是保守的,據此載荷設計的物項有足夠的強度和剛度水平。然而本文從結構動力學分析角度認為簡單地取載荷數值最大值而忽視載荷形狀,該處理方式不一定得到最大的管道系統動態響應,工程應用時需要認真甄別,本文將對這一情況進行詳細分析。
1 管端瞬態流計算
根據ANS58.2 附錄B,管道破裂后產生的管端瞬態流實際經歷3 個階段,如圖1 所示實線。第1 個階段,管道發生破口后1 ms 內瞬態流載荷值從零達到峰值(峰值為PA,其中P是初始壓力,A是管道內截面積);第2 個階段,從峰值經過一段時間波動達到穩定;第3 個階段,穩定持續噴射,噴射時間長度取決于壓力源[6]。

圖1 第1 種簡化且保守的管端瞬態流
同時ANS58.2 提供了一種計算管端瞬態流的簡化且保守做法:將上述第2 階段載荷拉平,如圖1 所示虛線,甚至認為壓力源足夠持續,可以直接從峰值處將上述第2、3 階段載荷拉平處理,如圖2 所示虛線。

圖2 第2 種簡化且保守的管端瞬態流
2 管道結構動力分析
根據前文所述,管道破裂后產生的動態效應有3 種,如圖3 所示,其中甩擊和瞬態流效應的結構動力分析需要用到管端瞬態流載荷。
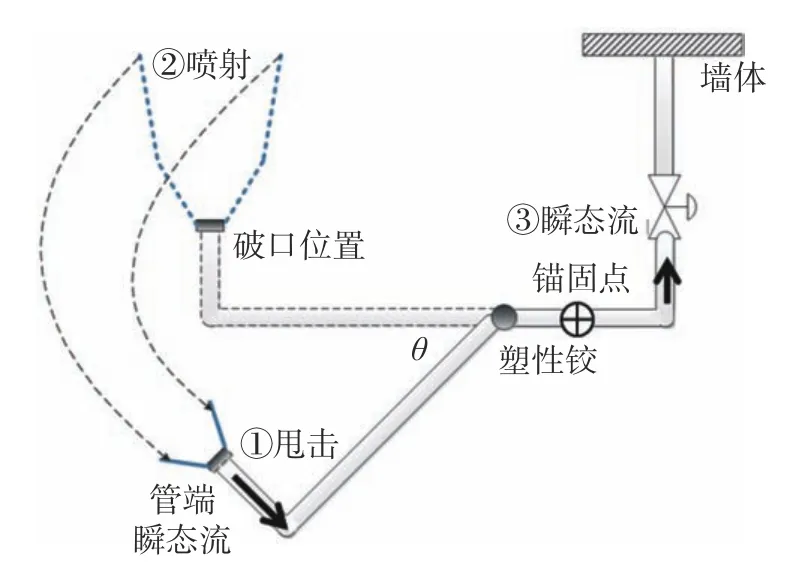
圖3 管道破損動態效應
2.1 甩擊分析
管道在管端瞬態流作用下形成塑性鉸產生甩擊效應[7],在這種情況下管道甩擊動能通過式(1)獲得,其中噴射反推力F按照前述章節取值簡化且保守的管端瞬態流載荷,如圖2 所示,就能夠得到最大的甩擊動能E,即甩擊防護設計就是保守的[8?11]。

式中:E為管道甩擊動能;F為噴射反推力即管端瞬態流載荷;CT為推力系數,取1;P為管道正常運行工況壓力;A為管道內截面面積;L為管端甩擊行程。以上各物理量都采用標準國際單位制。
2.2 管端瞬態流分析
當破口發生在錨固點附近,如圖4 所示管端瞬態流作用未能引起甩擊效應,而是在錨固點右側管道內因破口急劇泄壓產生壓力波載荷即瞬態流,作用在彎頭位置;瞬態流可能對管道系統造成破壞,從而需要開展管道在瞬態流作用下結構動力分析,保證錨固點右側管道的完整性,同樣需要用到管端瞬態流載荷。
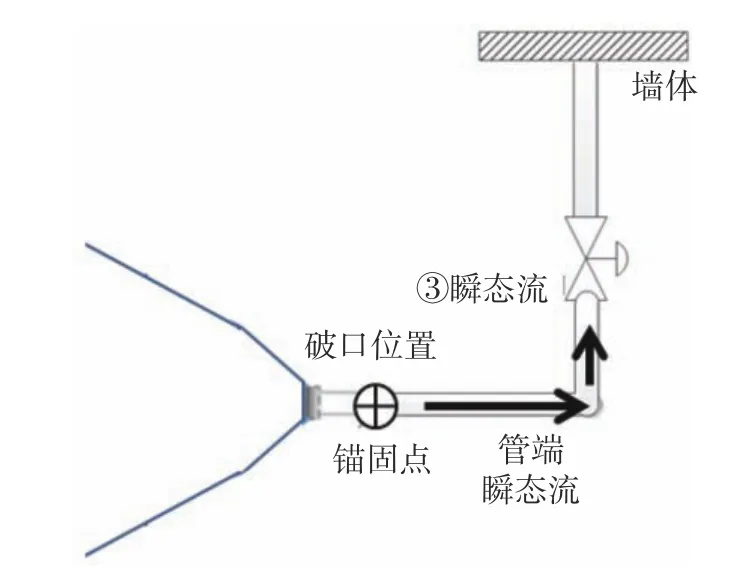
圖4 管道破損動態效應
然而前述第1 章關于管端瞬態流載荷簡化且保守的取值方法對管道在內部瞬態流作用下的結構動力響應不一定是保守的,下文以1 個單自由度無阻尼體系在2 種載荷形式下的強迫振動為例進行分析。
1)突加持續恒定載荷,如圖5 所示。

圖5 突加持續恒定載荷
設體系原處于靜止狀態,在t=0 時,突然加載FP,并一直作用在結構上,這種載荷形式類似于第1 章中簡化且保守的瞬態流載荷,載荷表示為
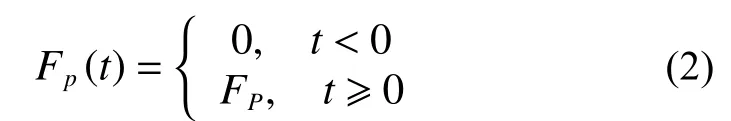
根據結構動力學理論公式經過3 步推導[12]可以得到質點動態響應。
a)列平衡方程:
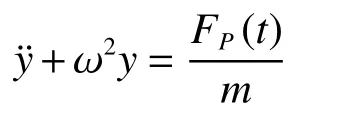
式中:y為質點位移,FP(t)為強迫載荷,m為質點質量,ω為體系圓頻率,t為時間,以上各物理量都采用標準國際單位制。
b)求解微分方程得質點位移公式:

c)將載荷式(2)帶入式(3)得質點位移:

對式(4)求一階得質點速度:

對式(4)求二階導得質點加速度:

式中:y(t)為質點位移,FP為恒定載荷,以上各物理量都采用標準國際單位制。
2)突加半正弦沖擊載荷,如圖6 所示。

圖6 突加半正弦沖擊載荷
設體系原處于靜止狀態,在t=0 時,突然加峰值為FP的半正弦載荷,在時刻t=u以后載荷突然消失,u為正弦載荷半周期長度,這種載荷形式類似于第1 章中未簡化且保守的瞬態流載荷,且認為壓力源是另一種極端狀態,不持續而是迅速喪失,載荷表示為

式中θ為載荷圓頻率,亦可表示為。
在該載荷作用下質點先后經歷受迫振動和自由振動2 個階段,根據結構動力學理論公式推導出質點在2 個階段的動態響應。
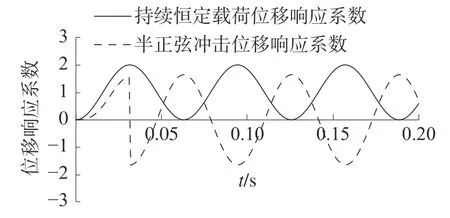
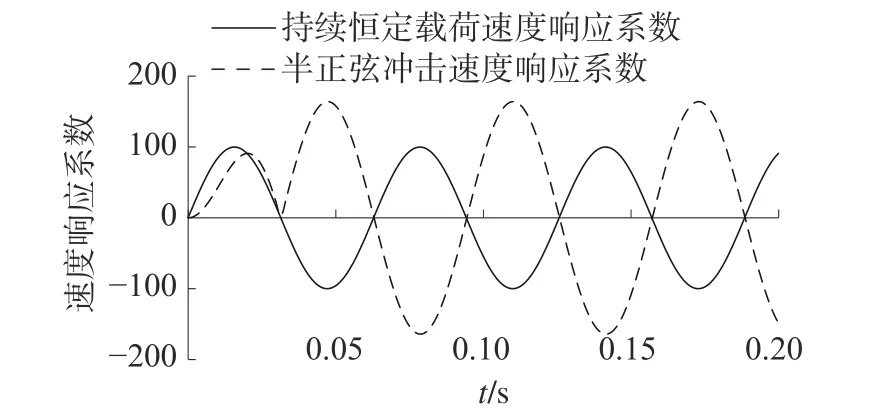
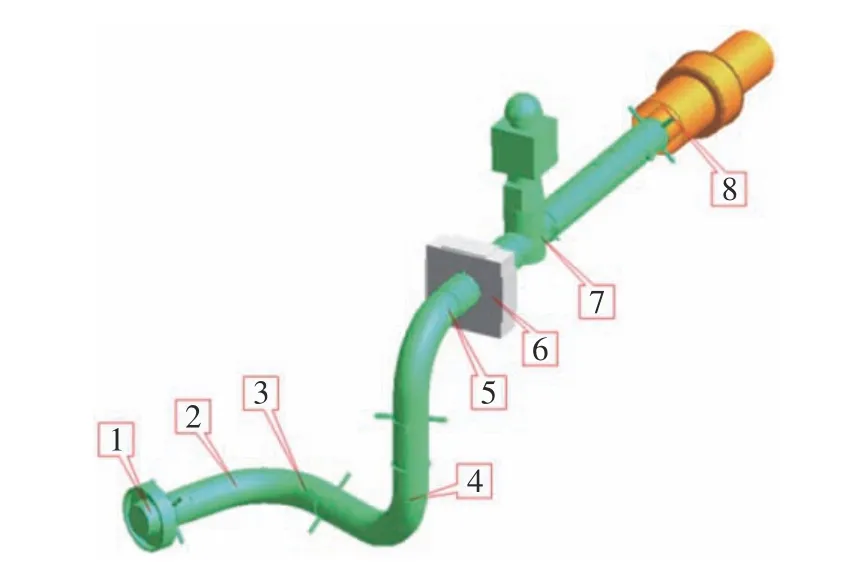
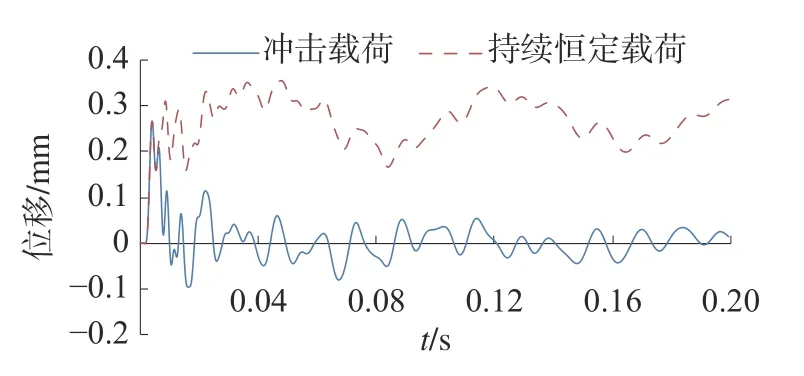
受迫振動階段(0 a)列平衡方程: b)求解微分方程得質點位移: 對式(7)求一階得質點速度: 對式(7)求二階導得質點加速度: 自由振動階段(t>u),根據結構動力學理論公式經過兩步推導[12]可以得到質點動態響應。 a)列平衡方程: b)求解微分方程并代入由式(7)、式(8)獲取的初始位移yt=u和初始速度則可以得出質點位移: 對式(10)求一階得質點速度: 對式(10)求二階導得質點加速度: 3)響應系數比較 已推導出的位移、速度、加速度公式都可以表示為f(θ,ω,t)·yst的形式,本文稱f(θ,ω,t) 為響應系數。通過設定單體系自振頻率ω,取不同的θ/ω比值,比較2 種載荷形式下響應系數的大小關系。 根據式(4)、(7)和(10),ω=100 rad/s,取不同的θ/ω比值,得到2 種載荷形式下位移響應系數關系,如圖7~8 所示。經過分析可知,突加持續恒定載荷的位移響應系數最大為2,突加半正弦沖擊載荷位移響應系數小于2。 圖7 位移響應系數(θ/ω ≈1) 根據式(5)、(8)和(11),ω=100 rad/s,取不同的θ/ω比值,得到2 種載荷形式下速度響應系數關系,如圖9~10 所示。經過分析可知,θ/ω比值接近1 時,突加持續恒定載荷的速度響應系數小于突加半正弦沖擊載荷速度響應系數;θ/ω比值遠離1 時,反之。 圖8 位移響應系數(θ/ω=10) 圖9 速度響應系數(θ/ω≈1) 圖10 速度響應系數(θ/ω=10) 根據式(6)、(9)和(12),ω=100 rad/s,取不同的θ/ω比值,得到2 種載荷形式下加速度響應系數關系,如圖11~12 所示。經過分析可知,θ/ω比值接近1 時,突加持續恒定載荷的加速度響應系數小于突加半正弦沖擊載荷加速度響應系數;θ/ω比值遠離1 時,反之。下文將通過一個實例驗證上述分析結果。 圖11 加速度響應系數(θ/ω ≈1) 圖12 加速度響應系數(θ/ω=10) 本文以圖13 所示的管道結構為研究對象,圖中1 號位置是C 型封頭,8 號位置是貫穿件,6 號位置是導向支架(下文簡稱GL),7 號位置是閥門;用ANSYS 程序[13]建立管道有限元計算模型,直管采用PIPE16 單元[14],彎管采用PIPE18 單元,GL(導向)支架采用COMBIN14 單元,閥門偏心采用MASS21單元;圖13中的1號位置和8號位置6 個自由度全約束,6 號位位置約束水平和豎向平動[15]。 圖13 管道結構示意 假定1 號位置C 型封頭的下游(管內介質從8 號位置流向1 號位置)出現破裂,本文根據分析需要,不考慮其他彎頭處瞬態流載荷,僅對2 號位置管端瞬態流進行分析,分別考慮突加持續恒定載荷和突加沖擊載荷2 種載荷形式,如圖14 所示。 圖14 2 號位置管端瞬態流載荷 該管道單元在突加持續恒定載荷作用下的管道位移比突加沖擊載荷大,如圖15 所示,根據前文理論分析可知,持續恒定載荷形式比脈沖形式的載荷對位移影響更大。 圖15 管道3 號位置水平向位移 該管道單元在突加持續恒定載荷作用下的閥門加速度比突加沖擊載荷小,如圖16 所示,根據前文理論分析可知,當脈沖形式的載荷頻率與自振頻率接近時,比持續恒定載荷形式對加速度影響更大。 圖16 閥門水平向加速度 本文從結構動力學角度,對管端瞬態流簡化且保守的計算方法進行了理論和實例分析,得到如下結論: 1)動態載荷峰值相同的情況下,持續恒力荷載比沖擊荷載對結構位移響應的影響大;且沖擊荷載頻率越接近結構自振頻率,對結構位移響應的影響越大。 2)動態載荷峰值相同情況下,沖擊荷載頻率越接近結構自振頻率,對結構速度和加速度響應的影響越大;且接近一定程度時,沖擊荷載對結構速度和加速度響應的影響會超過持續恒力載荷。 3)管端瞬態流簡化計算方法,即假定壓力源足夠持續,載荷峰值處拉平處理,對管道甩擊分析是保守的,計算得到最大的甩擊力;對結構動力分析的位移計算是保守的,計算得到最大位移。 4)管端瞬態流簡化計算方法,即假定壓力源足夠持續,載荷峰值處拉平處理,對結構動力分析的加速計算是不保守的,當真實的脈沖載荷頻率接近結構自振頻率時,瞬態流簡化拉平載荷計算得到的加速度比脈沖載荷計算得到的加速度小。 5)實際工程中,壓力源很難實現足夠持續,實際更偏向產生脈沖載荷,評價管道系統中部件在管端瞬態流作用下的加速度影響時,管端瞬態流簡化計算方法得到的加速度值不是最大情況,偏不保守。


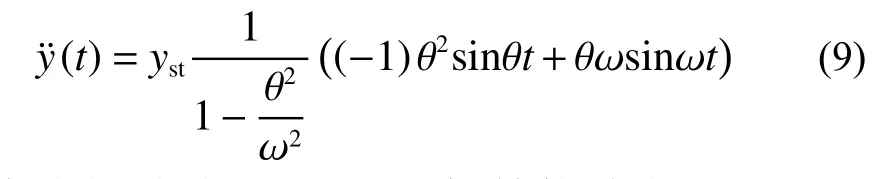
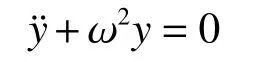
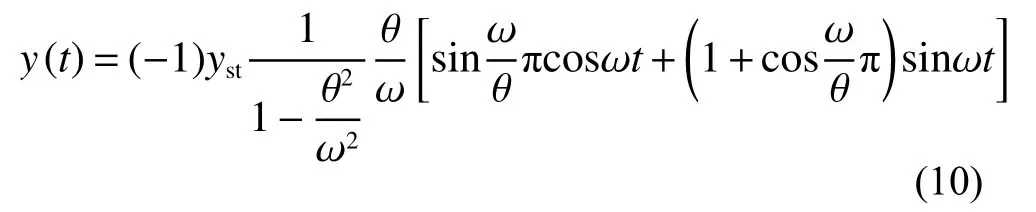






3 實例分析


4 結論

