車載慣導系統抗擾動自對準方法對比研究

趙 彤，李 群，蒲小平, 吳亮華，胡奇林

(1.北京自動化控制設備研究所，北京 100074; 2.空軍裝備部， 北京 100843)

0 引言

陸基機動平臺及裝備用慣導系統進入正常導航前需要具備較高的初始姿態精度，利用經緯度位置信息、重力加速度和地球自轉角速度等信息進行自主對準。車載慣導系統[1]初始自對準一般包括粗對準和精對準2個階段，粗對準根據陀螺和加表測量信息解算出粗略的初始姿態陣[2-3];精對準采用濾波估計方法，根據慣導系統誤差模型，利用零速信息，通過Kalman濾波器對慣性器件誤差和姿態誤差角進行最優估計和校準，從而得到慣導系統更為精確的初始姿態。實際工程應用中，當車輛受到大幅度干擾，如發動機啟動、風擾和人員走動等情況時，車輛將不再處于絕對零速狀態，自對準精度將受到影響。因此，車載慣導自對準的抗干擾能力是決定其環境適應性和導航精度的關鍵，需開展深入研究。

除目前廣泛應用的濾波估計方法外，確定性姿態算法[4-6]也是近年來廣泛研究的初始對準方法。20世紀60年代以來，G.Wahba提出了利用觀測矢量進行星體姿態確定的最小二乘優化問題[7]；Daveport提出了各種Q-method方法[8]，利用四元數優化獲得姿態陣。

本文對目前常用的慣性系解析自對準、Kalman濾波估計自對準和慣性系奇異值分解[9](Singular Value Decomposition，SVD)自對準等三種方法進行了研究和對比分析，根據三種對準方法各自的實現原理，提出了一種有針對性的抗擾動優化方法，并通過了數學仿真分析和車載試驗驗證，最終得出了研究結果。

1 自對準方法

常用的初始對準方法包括解析對準[10-11]與Kal-man濾波對準。

1.1 慣性系解析對準方法

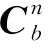
(1)

(2)

(3)

(4)

將式(1)代入式(4)得

(5)

(6)

可表示為

(7)

其中

取2個適當間隔的不同時刻，工程上自對準時間設定為300s(一般取tl=150s，tm=300s)。

再利用雙矢量定姿算法進行矩陣運算，即可求得常值矩陣:

(8)

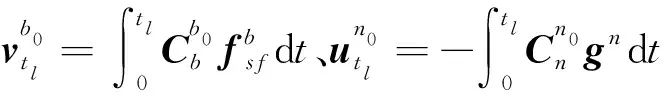
1.2 Kalman濾波自對準方法

目前，Kalman濾波技術應用廣泛，是一種線性最小方差估計算法。在慣導系統初始對準中，通常利用Kalman濾波器對系統的初始姿態角、速度、位置和慣性器件誤差進行建模并估計，通過反饋修正實時對誤差進行補償。通常粗對準獲得的方位角誤差在3°以內，可以實現姿態誤差方程小角度近似,一般采用速度匹配的方式進行對準。

Kalman濾波模型如下

(9)

根據姿態、速度和位置誤差方程，列出Kalman濾波12維狀態變量

X=[δVnδVuδVeφnφuφe

(10)

濾波觀測量為

(11)

1.3 基于SVD的慣性系自對準方法

給定三維空間中有m個不共面的矢量，在2個直角坐標系下的投影分別表示為ri和bi(i=1,2,…,m)，并滿足

bi=Ari+Δbi

(12)

其中，Δbi為量測噪聲。由于存在誤差，所以多矢量定姿的實質是找到姿態矩陣A使測量誤差最小，并滿足最小二乘最優估計，構造損失函數

(13)

其中，wi為權重系數，一般取wi=1。

損失函數進一步展開可得

(14)

第一項為已知量，與A陣無關，為使損失函數J(A)達到最小，等價于第二項最大，重新構造函數

(15)

對式(15)作進一步變化，可得

(16)

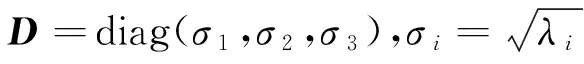
通過矩陣B的奇異值分解，可得最優姿態矩陣A=U·diag(1,1,det(UV)T)VT。

2)根據式(17)和式(18)計算比力觀測矢量rk和bk

(17)

(18)

根據式(19)和式(20)計算每一時刻矩陣Bk

ΔB=bk(rk)T

(19)

Bk=Bk-1+ΔBk

(20)

矩陣Bk運用遞推累加的形式來更新，遞推的初值設置為0，B0=03×3。

2 抗擾動處理

1)對于適用于晃動基座的慣性系解析對準，根據雙矢量定姿的原理[14-15]，取適當間隔的2個不同時刻，利用2個時刻的測量信息求取姿態矩陣。當外界受到大的干擾影響時, 僅取2個時刻的測量信息對準結果必然受到影響。為了降低晃動對精度的影響，本文在原有基礎上進行了改進，將原來對準時選取的2個點改成兩段時間平均后的點(tl=120s～180s，tm=240s～300s)。

對一套精度為0.003(°)/h的激光陀螺捷聯慣導系統進行試驗驗證，將慣導系統安裝在試驗車上，車輛處于受干擾狀態(發動機怠速啟動、人員上下)。每次對準時間5min，一次上電測試20次。改進前后自對準航向角重復性精度對比圖如圖1所示。

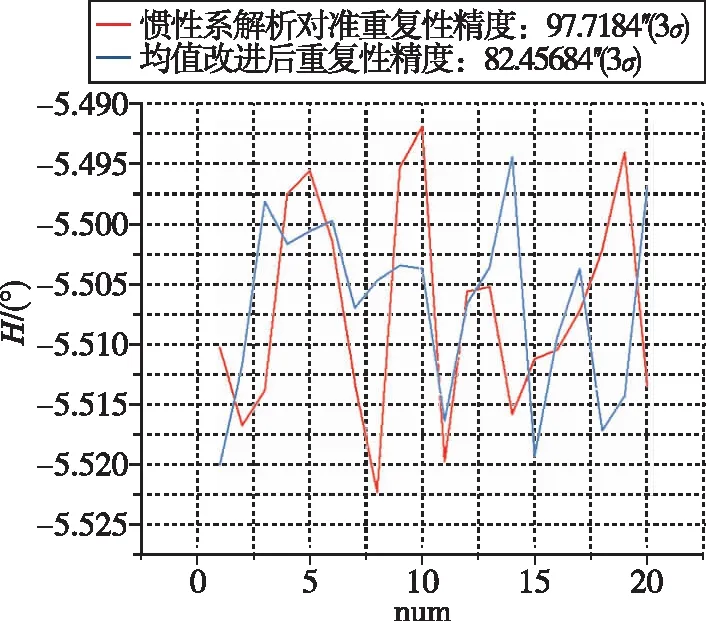
圖1 慣性系解析對準及改進后重復性對比圖Fig.1 Comparison of repeatability accuracy of inertial frame analytical alignment with that of improved heading angle

經過試驗驗證對比可得，均值改進后的對準方法比傳統方法精度提升了15″(3σ)，抗晃動性能得以提升。

2)基于速度匹配的Kalman濾波估計，在車輛晃動的影響下，對準航向角收斂時存在噪聲引起的震蕩。本文在原有算法的基礎上進行改進，采用速度積分匹配的方式，能夠起到平滑作用，對系統的誤差模型進行調整，Kalman濾波15維狀態變量和量測量如下:

X=[δlnδluδleδVnδVuδVeφnφuφe

(21)

(22)

式中

δln、δlu、δle分別為北、天、東速度誤差積分。

這座工廠從2019年夏天起，將成為該品牌首款混合動力轎跑車Polestar 1的全球生產基地。Polestar 1能夠輸出600馬力的最大功率，和1000牛·米的峰值扭矩，它在純電動模式下可以行駛150公里。作為旗艦車型，它的售價預計在15．5萬歐元左右（約合125萬元人民幣，此處為未計算補貼價格，下同）。而將緊隨其后推出的Polestar 2，是一款完全由電力驅動的車型，預計定價從4萬歐元起（約合32萬元人民幣）。銷售思路有所創新，以定制租賃為主，包括按月付款的全包式購車模式。

在與1)相同條件下進行試驗驗證， 速度匹配和速度積分匹配對比圖如圖2所示。

圖2 Kalman速度積分匹配與速度匹配航向角收斂對比圖Fig.2 Comparison of course angle convergence between velocity integral matching with velocity matching

速度積分匹配與速度匹配相比,經試驗驗證，航向角收斂更加平滑,收斂速度更快，精度更高，抗擾動能力更強。

3)選擇比力矢量作觀測量，航向角收斂時也存在震蕩。為了提升SVD算法的性能，本文通過姿態陣更新隔離外界角運動干擾，對比力矢量積分并增加低通濾波器降低線振動的影響，從而提升系統的抗晃動能力。

改進后的算法原理圖如圖3所示。

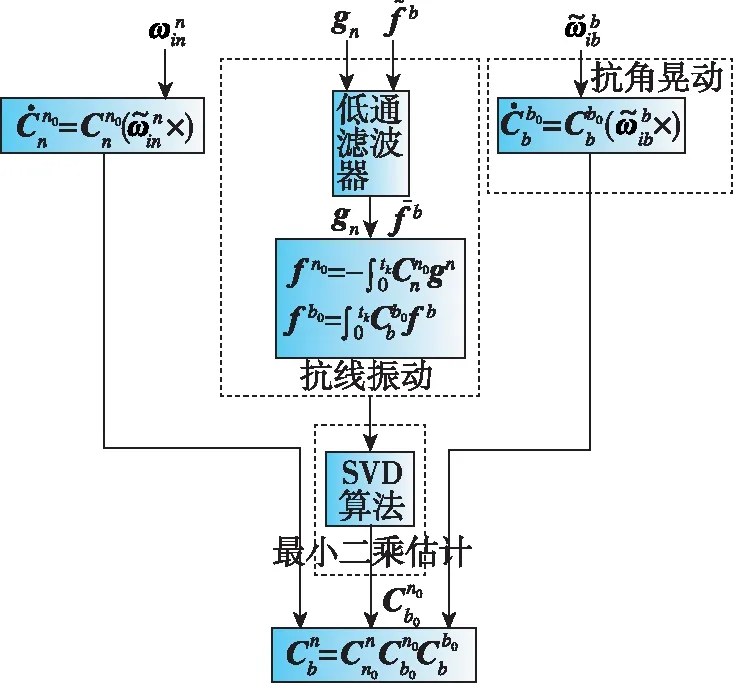
圖3 慣性系SVD算法原理圖Fig.3 Schematic diagram of inertial frame SVD algorithm

改進措施如下：

(1)隔離角晃動干擾

(2)隔離線振動干擾

a)比力積分

(23)

(24)

b)低通濾波器

選擇慣性系速度作為觀測向量，為進一步消除線振動干擾的影響，增加一個數字濾波器以過濾掉噪聲干擾，保留正常信號。gn和fb為低頻信號，遠低于Vn等干擾量的頻率，通過數字濾波器的方式，建立在對晃動干擾頻譜分析的基礎上。選擇二型結構IIR低通濾波器，設計指標為: 采樣頻率200Hz，通帶截止頻率10Hz，阻帶截止頻率20Hz，通帶衰減1dB，阻帶衰減80dB，10階IIR低通濾波器。具體系數由Matlab工具箱輔助獲得。

與方法1)相同條件下進行試驗驗證，對加速度計數據做出頻譜特性分析，如圖5所示，濾波器處理前后航向角收斂對比圖如圖6所示。

圖4 車載怠速條件下加速度計輸出曲線圖Fig.4 Output curve of accelerometer under vehicle idling condition

圖5 車載怠速條件下加速度計幅頻特性圖Fig.5 Spectrum characteristic diagram of accelerometer under vehicle idling condition

圖6 濾波器處理前后航向角收斂對比圖Fig.6 Comparison of course angle convergence between velocity observation vector and force observation vector in inertial frame

經過試驗可得，濾波器處理后的航向角收斂更加平滑。

3 車載試驗驗證

最后對三種抗擾動自對準方法進行車載對比試驗，試驗條件和過程與前文所述一致，每次對準時間5min，一次上電測試20次。利用三種抗擾動自對準方法對相同的實測數據進行仿真分析，試驗車和慣導系統圖片如圖7和圖8所示，試驗結果如下。

圖7 試驗車照片Fig.7 Photo of test vehicle

圖8 捷聯慣導系統照片Fig.8 Photo of the strap-down inertial navigation system

1)對相同實測數據進行仿真分析，三種自對準方法航向角重復性精度對比圖如圖9所示，慣性系解析、Kalman濾波估計和慣性系SVD三種方法的航向角均值分別為-5.5078°、-5.5052°和-5.5074°。

圖9 三種自對準方法重復性精度對比圖Fig.9 Comparison of repeatability accuracy of the three self alignment methods

2)為方便比較，將慣性系SVD解析對準30s時刻的航向角作Kalman濾波自對準方法的初始航向角，慣性系SVD繼續進行解算，給出30～300s時間內Kalman濾波估計自對準和慣性系SVD解析自對準航向角收斂速度對比圖如圖10所示。

圖10 SVD和Kalman航向角3min/4min/5min收斂對比圖Fig.10 Comparison of SVD and Kalman heading angle convergence for 3/4/5min

車載晃動基座條件下，對慣性系解析自對準、Kalman濾波估計自對準和慣性系SVD自對準三種結果進行對比分析。由圖9可知，后兩者重復性精度要優于前者；由圖10可知，慣性系SVD與Kalman濾波估計相比對準精度相當，收斂速度相當。

從慣性系解析自對準、Kalman濾波估計自對準和慣性系SVD自對準三者的計算過程和試驗結果對比可得：

1)傳統慣性系解析自對準的計算過程簡單，計算量小，但抗擾動能力相對弱，對準精度相對低，對于對準精度要求不是很高或者純靜態情況下可以采用；

2)Kalman濾波估計自對準方法目前應用最廣泛，計算量大于慣性系解析對準，對準精度高，抗擾動能力強，但需要姿態初值和濾波參數；

3)慣性系SVD自對準的計算量和對準精度與Kalman濾波估計自對準相當，抗擾動能力強，無需姿態初值且不需要建立模型和設置參數，可以實現短時間對準。

4 結論

本文對慣性系解析、Kalman濾波估計和慣性系SVD三種車載抗擾動自對準方法進行對比研究，結果表明，三種方法各有優點，慣性系解析自對準方法計算簡單，適用于低精度要求或純靜態條件；慣性系SVD自對準方法既可以利用陀螺輸出進行姿態陣計算隔離外界角晃動，同時又具備濾波作用，可以達到與Kalman濾波方法相當的對準精度，具有快速收斂性、無需先驗信息即可獲得最優解、工程適用性高等優點。