基于虛擬圓球模型的格網SINS/GNSS極區組合導航方法

葛浩冉，徐 祥，黃 玲，趙鶴鳴

(蘇州大學電子信息學院，蘇州 215006)

0 引言

近年來，北極的戰略價值不斷提高，受到國際社會的普遍關注。可以預見，越來越多的極地考察任務將實施，極區精確導航將成為支撐極地考察的核心技術之一。慣性導航系統可以全自主地完成導航工作，是極區導航的主要設備。現代導航均以經線作為航向參考基準，使用經緯度來表示位置，而北極附近經線迅速收斂于極點，造成建立相對經線的航向參考基準越來越困難，使得傳統的慣性導航系統在極區無法定向。

目前，極區慣性導航的主流解決方案有橫向坐標系[1]和格網坐標系[2]導航算法。地球作為導航解算的參照體，其模型的選擇是慣性導航系統的重要參數，常采用傳統圓球模型和旋轉橢球模型對地球作近似描述。在文獻[3]中提出了圓球模型下的慣性導航力學編排，計算簡單但不可避免地產生原理性誤差。在文獻[4]中提出了橢球模型下的慣性導航力學編排，可以避免圓球模型帶來的原理性誤差，但是引入曲率半徑的計算，使得導航解算過程復雜化。在文獻[5]中提出了虛擬圓球的概念，利用虛擬圓球模型簡化導航力學編排，其精度與橢球模型一致。分析慣性導航系統的誤差特性是抑制導航誤差、提高導航精度的重要步驟，在文獻[6-7]中為了簡化誤差方程推導，均將地球視作圓球模型，以及在文獻[8-9]中阻尼技術和文獻[10-11]中組合導航系統設計均采用地球圓球模型。對導航系統進行性能評估與驗證，實地測試是不可或缺的部分。由于極區實測獲取數據難度大，因此獲取極區軌跡數據的主要思想是將中低緯度實驗數據通過數學方法轉換到高緯度地區，目前已有文獻中的主要方法包括緯度增量法[12]、坐標系旋轉法[13]和姿態速度不變法[14-15]。通過對比分析，姿態速度不變法可以在轉換過程中減少軌跡壓縮，同時滿足極區的地理特性。

針對上述提出的采用圓球模型誤差特性進行組合導航系統設計的問題，本文在文獻[5]提出的虛擬圓球模型的基礎上推導誤差方程，設計格網系組合導航系統，實現了捷聯慣導地球模型與濾波模型的統一。本文添加了跑車實驗，使用文獻[14]中的格網姿態速度不變的(Grid Attitude and Velocity Invariant Method，G-AVIM)虛擬極區方法，將低緯度實驗數據通過算法轉換到極地區域。實驗數據結果表明：基于虛擬圓球模型下的格網系捷聯慣性導航系統(Strapdown Inertial Navigation System，SINS)/全球衛星導航系統(Global Navigation Satellite Systems，GNSS)組合導航系統可以完成極區導航工作。

1 導航力學編排

采用格網系進行極區慣性導航，推導基于虛擬圓球模型下的導航力學編排。記地球坐標系為e系，載體坐標系為b系，地理坐標系為g系，格網坐標系為G系。

1.1 格網坐標系

設載體的位置為P，格網坐標系的定義如圖1所示，以O為球心，地球坐標系記為(xe,ye,ze)，以P點處平行于本初子午面的平面作為格網平面，格網平面與當地切平面的交線定義為格網北向，格網天向與地理天向重合，格網東向在切平面內與格網北向和天向構成右手直角坐標系。格網北向與地理北向之間的夾角σ稱為格網方位角。地理坐標系各軸向量記為(E,N,U)，格網坐標系各軸向量記為(GE,GN,GU)。λ和L分別表示P點處的經度和緯度。

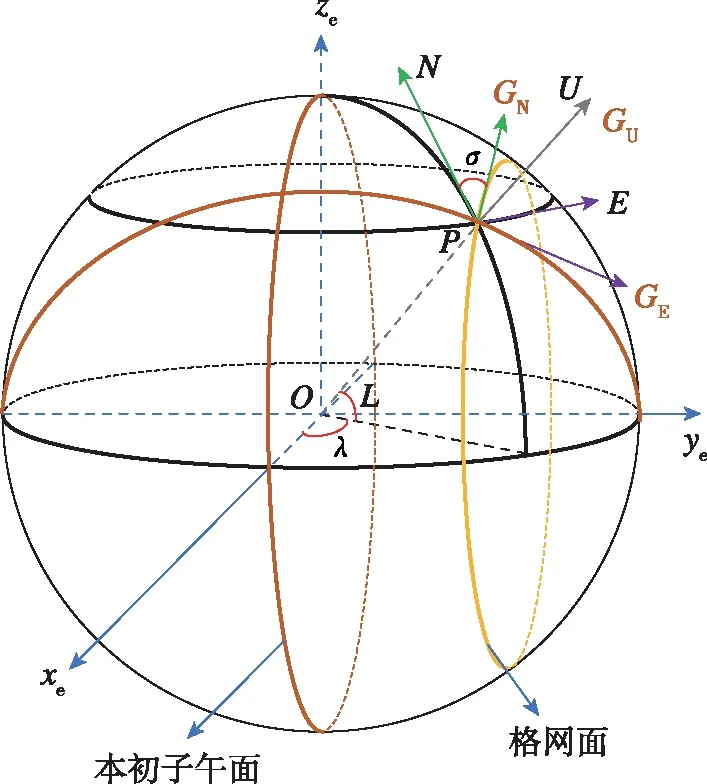
圖1 格網坐標系Fig.1 Grid coordinate system

格網坐標系與地理坐標系之間的轉換關系為

(1)

對于北半球，格網方位角σ的正弦和余弦可以描述為

(2)

(3)

1.2 慣導力學編排

虛擬圓球模型是以載體所在的卯酉圈半徑作為圓球半徑人為構造的圓球。在圖2中，Re和Rp分別為地球橢球模型的長軸半徑和短軸半徑；P點的地心緯度和地理緯度分別為Le和L；以O點為圓心，OP為半徑所畫虛線為虛擬圓球。

圖2 虛擬圓球原理圖Fig.2 Virtual sphere schematic diagram

設虛擬圓球的半徑為Rt，具體的計算過程和符號說明可參見文獻[5]

(4)

基于虛擬圓球模型的格網系導航力學編排的姿態方向余弦矩陣、速度和位置微分方程[16]可表述為

(5)

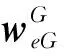
(6)

其中，格網系下的補償速度為

K為參考橢球變換為虛擬圓球的尺度系數矩陣，k為尺度變換系數，具體符號說明可參見文獻[5]

2 導航誤差方程

現有文獻中，由于橢球模型下的格網系編排復雜，為簡化誤差推導方程，均近似采用圓球模型。本文將推導基于虛擬圓球模型的格網系誤差方程。

地球坐標系和直角坐標系之間的轉化關系為

(7)

式中，Rth=Rt+h，h為載體高度；e為橢球第一偏心率。

對式(7)求微分得

δRe=MPR·δP

(8)

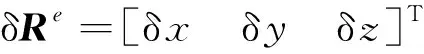
(9)

(10)

式(10)中，Ω為地球自轉角速度。

(11)

由式(8)和式(11)可以得到

(12)

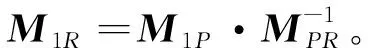
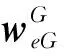
(13)

其中

(14)

(15)

式中

由式(8)和式(13)可以得到

(16)

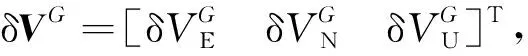
(17)

3 格網系組合導航算法

現有文獻在設計組合導航的濾波模型時，為簡化計算將地球視作圓球。本文為提高組合導航精度，將捷聯慣導機械化的地球模型與濾波模型進行統一，均采用虛擬圓球模型。設計了基于虛擬圓球模型的格網系SINS/GNSS組合導航系統。

3.1 系統狀態方程

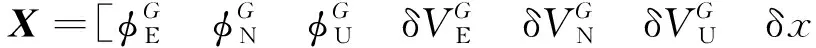
由誤差方程可得系統狀態方程為

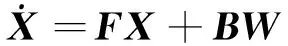
(18)

式中，F為狀態轉移矩陣；B為系統噪聲分布矩陣；W為系統噪聲向量。

F=

(19)

(20)

(21)

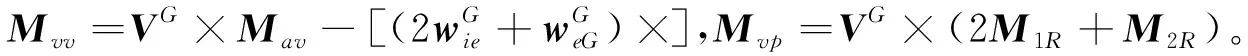
3.2 系統量測方程

在高緯度地區GNSS可輸出ECEF坐標系表示的位置，格網系輸出位置也采用ECEF坐標系，因此，組合導航系統選擇格網SINS位置與GNSS位置的測量差作為組合導航系統的觀測值，建立量測方程為

(22)

則量測方程的矩陣形式為

Z=HX+V

(23)

式中，H為量測矩陣，V為量測噪聲。

(24)

其中，I3表示三階單位矩陣。

4 實驗與分析

為驗證基于虛擬圓球模型下格網系SINS/GNSS極區組合導航算法的正確性和可行性，傳統的純數學仿真不能反映環境影響和完全模擬載體運動，本文使用文獻[14]中的虛擬極區方法，將低緯度跑車實驗數據通過G-AVIM算法生成極地地區數據。

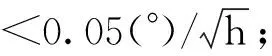
圖3 實驗車與設備Fig.3 Experiment vehicle and equipment

現場實驗在蘇州市完成，起始位置為[31.312164°N 120.648157°E 4.5m]，時長2.5h，最大速度約為25m/s。建立極區軌跡，將起始點設置為北極點90°N，轉換后的極區經緯度軌跡如圖4所示。可以看出，該軌跡在極點附近產生并穿過極點，經度符合實際中極區經度特點。仿真結果如圖5～圖7所示。

圖4 極區軌跡與經緯度圖Fig.4 Latitude and longitude map of polar track

圖5 格網系姿態誤差Fig.5 Attitude error of grid system

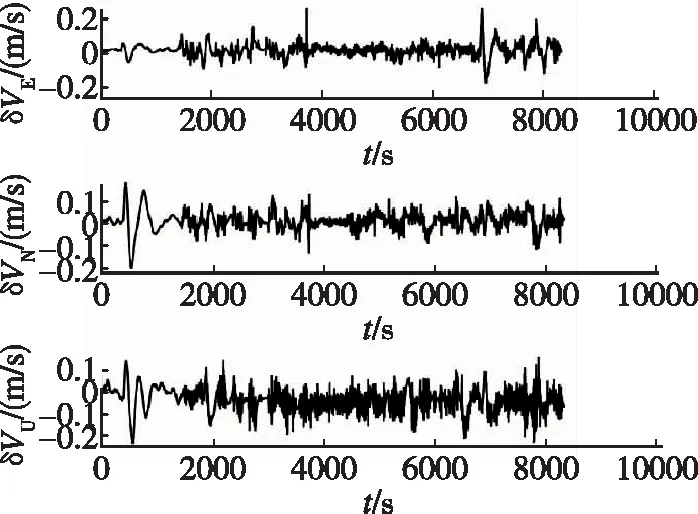
圖6 格網系速度誤差Fig.6 Velocity error of grid system

圖7 格網系位置誤差Fig.7 Position error of grid system

圖5～圖7所示為基于虛擬圓球模型的組合導航系統誤差圖，由圖5姿態誤差可以看出，水平姿態誤差角十分平穩，誤差基本在0.2′左右小范圍波動，最大誤差不超過0.3′，由于慣性器件零偏導致航向誤差角在前2000s最大誤差達到1°，后面隨著載體做轉彎等機動，使得慣性零偏得到補償，航行姿態角趨于穩定，誤差不超過0.2′；圖6速度誤差收斂后穩定在0.1m/s，最大誤差不超過0.2m/s；圖7為ECEF坐標系下的位置誤差，水平方向位置誤差不超過5m，垂直方向誤差不超過10m。從實驗結果分析可知，首先，基于虛擬圓球模型的格網系慣性導航算法可以完成極區的導航任務，在穿過極點與極點附近時都不會發生跳變現象，克服了傳統中低緯度慣導的缺陷，驗證了本文方法的可行性；其次，組合導航系統的定位誤差不超過5m，可以滿足極區航行的精度要求。

5 總結

本文針對格網系組合導航系統模型不統一的問題，提出了一種基于虛擬圓球模型下的格網系組合導航系統，算法分析與實驗結果表明：

1)虛擬圓球模型下的格網系力學編排通過對速度的補償，彌補了圓球模型下存在的原理性誤差，簡化了橢球模型的計算復雜度，因此可以簡化系統誤差方程的推導。

2) 將捷聯慣導地球模型與濾波模型進行統一，均采用虛擬圓球模型，不再是橢球模型的慣導更新算法與圓球模型的濾波算法，使得狀態轉移矩陣更準確，同時統一的模型還可以簡化系統設計。

3)本文不再使用純數學仿真，而是進行跑車實驗，利用虛擬極區的方法將軌跡數據轉換到極區，驗證了實驗的有效性和可行性，更具有說服力。