低風速涌浪條件下浪致應力的研究

潘偉，鄒仲水，宋金寶*，黃健

( 1. 浙江大學 物理海洋研究所，浙江 舟山 316021；2. 中國氣象局廣州熱帶海洋氣象研究所，廣東 廣州 510640)

1 引言

海洋和大氣是一個緊密的耦合系統，發生在海氣界面的動量通量交換對海洋、大氣模式的精準預報至關重要，是深刻理解多尺度海氣相互作用的關鍵因素之一。

Monin-Obukhov 相似理論(MOST)[1]是大氣邊界層的重要理論，研究者們通常基于MOST將不同觀測高度、穩定度的拖曳系數(CD)轉換為10 m高度處中性條件下的拖曳系數(CDN)以分析邊界層動力學特征。隨著觀測數據的不斷增多，研究發現同風速下不同觀測之間的CDN結果存在顯著差異，這種差異在低風速下尤其明顯。以往的研究認為這是由于風浪的狀態(如波齡、波陡等)造成的[2–5]。然而，最新研究表明風浪狀態只能部分解釋觀測所得CDN的離散特性，涌浪和邊界層的相互作用是導致CDN離散的另一個可能原因，具體表現在以下幾個方面。

（1）涌浪影響動量通量傳輸過程。海浪與大氣邊界層之間通過浪致雷諾應力進行動量傳輸。風浪引起的浪致雷諾應力與局地風平衡，而涌浪的傳播速度比局地風速大，在涌浪誘導下，產生新的浪致雷諾應力[6]。涌浪與風浪的浪致雷諾應力疊加在一起，使得同等風速下動量總通量不再是簡單的關于風浪波齡、波陡的函數[7]。在涌浪存在的情況下，如果只考慮風浪對動量通量的貢獻而忽略涌浪的影響，會給拖曳系數造成很大不確定性。

（2）涌浪影響MOST的適用性。Zou等[8]研究顯示，MOST只能刻畫邊界層由剪切和浮力產生的湍流，而在涌浪存在的情況下，邊界層湍流除了受剪切和浮力影響，還受涌浪激發的擾動影響。在此情況下繼續采用MOST會引入誤差[9–10]。

（3）涌浪造成風應力偏離主風方向。Geernaert[11]根據Navier-Stokes方程發現邊界層內風應力方向與主風向基本一致，它們之間的夾角小于5°。但涌浪的傳播方向可能和風向偏差較大，其誘導的浪致雷諾應力與湍流應力滿足矢量合成法則，這將導致總風應力偏離主風方向。所以，如果把主風向上的風應力作為動量通量會帶來較大誤差[12–14]。

（4）涌浪通過調制風浪間接影響邊界層。涌浪通過影響海面粗糙度從而間接影響動量通量，動量通量又反過來影響風浪的成長，形成海浪與風的耦合過程。例如Geernaert[11]和Grachev等[12]的研究顯示，涌浪可能導致風浪向高頻偏移[15]或者平衡域能量降低[16–17]，使得海浪與邊界層相互作用變得更為復雜。

為了研究涌浪對邊界層的影響，目前采用的方法主要是譜方法。例如許多研究顯示大氣邊界層中的湍流譜存在一個與涌浪同頻率的譜峰[13–14,18–19]。除此之外，在涌浪條件下，H?gstr?m 等[18]、Young[20]和 Kahma等[21]的研究發現協譜可以記錄涌浪的浪致雷諾應力。據此，人們給出了大量的涌浪向大氣傳輸動量通量的證據。除此外，還有研究顯示涌浪的浪致雷諾應力不僅可以為負(海洋向大氣傳輸能量)，也可以為正(從大氣吸收能量)[14]。而且，H?gstr?m 等[22]研究發現上述兩種情況在風速為4.5 m/s時發生反轉。

浪致雷諾應力的正負可以產生不同的效果，如Babanin等[9]研究顯示當浪致雷諾應力為正時，海浪邊界層內的風速比MOST結果要小；反之，浪致雷諾應力為負時，海浪邊界層內的風速比MOST結果要大[23]。因此準確判斷浪致雷諾應力的變號條件對海氣耦合模式尤為重要。考慮到涌浪與大氣邊界層的相互作用是一個復雜的過程，而風速并不是浪致雷諾應力變號的唯一條件，本文利用茂名海上綜合觀測平臺實測數據初步探討浪致雷諾應力變號的條件。除此之外，浪致雷諾應力的大小對海氣相互作用的研究也具有重要意義，本文擬從觀測數據中提取浪致雷諾應力并檢驗當前浪致雷諾應力計算模型的準確性。

2 研究方法

在貼近海洋表面的大氣邊界層中，總應力可以分為3部分

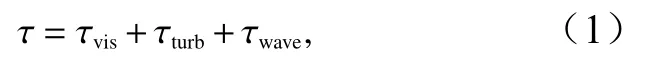
式中，τvis是分子黏性應力，由相鄰流層間的摩擦產生，用于阻滯流層間的相對運動。在分子黏性子層以外，分子黏性應力遠遠比湍流應力小，因此在這里可以忽略不計。τturb是由平均風速剪切或者浮力產生的湍流應力，通常為正值，代表著大氣向海洋輸入能量；τwave是波浪引起的浪致雷諾應力，當海浪從風中吸取動量通量時為正值，當大氣從海浪中汲取能量時為負值。

根據Grachev等[12]，將海氣間的應力寫為譜的形式

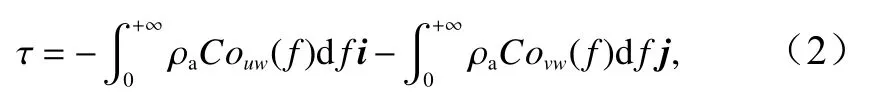
式中，ρa是空氣密度；Co是協譜；f是頻率；u，v和w代表去除平均風速的三維雷諾脈動；i和j分別代表x（順風向）和y（側風向）軸的單位矢量。實際上，協譜可能為正也可能為負。Couw為負表示大氣向海洋傳輸能量；Couw為正表示海洋向大氣傳輸能量；Covw為正（負）表示風應力偏向風的右（左）側。觀測[24]顯示，貼近海洋表面的湍流中除了剪切和浮力生成的湍流外，還有海浪誘導的脈動。因此式（1）和式（2）進一步寫為

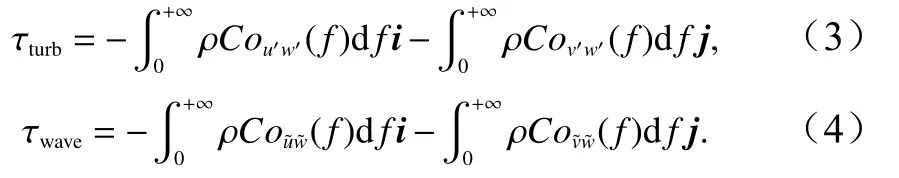
在上述公式中，我們忽略了湍流與海浪擾動交叉項，這是因為我們的觀測顯示該項比湍流應力和浪致雷諾應力小約10個量級，其影響可以忽略不計。

式（2）至式（4）表達的物理意義是海氣界面湍流應力和浪致雷諾應力在頻率上的分布。因為海浪頻率 (約 0.05～10 Hz)與湍流頻率 (10?4～10 Hz)相比為窄譜，而海浪誘導的脈動與海浪頻率一致，據此可以根據積分公式（2）和式（3）、式（4）研究海浪對湍流應力的影響[14,22,25]。

根據式（2），我們定義Ogive曲線為協譜從當前頻率f到最高頻率fmax的積分，表達式如下

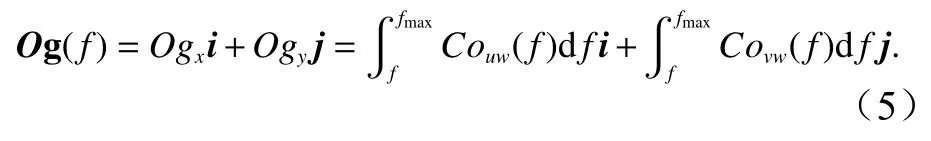
從上面可見，當協譜(Couw和Covw)體現出涌浪對邊界層的影響時，Ogive曲線因包含涌浪效應能夠更直觀的展現出這種影響。

對于浪致雷諾應力，可以通過對海浪譜進行積分來獲得總體的浪致應力[26]

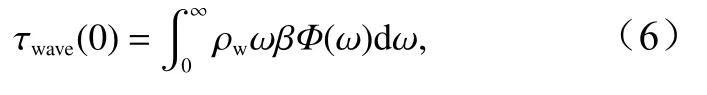
式中，ρw是水的密度；β是波浪的增長/衰減率；Φ(ω)是海浪譜；ω是海浪譜的角頻率。研究顯示浪致應力隨高度呈指數衰減[27]。因此，在不同高度的浪致應力為

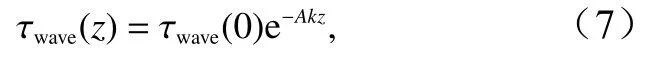
式中，k是波數；A是衰減系數。一些學者通過實測數據和數值模擬對衰減系數進行了研究[18,28–30]，H?gstr?m等[18]認為衰減系數范圍為1.0～2.1；而Hanley和Belcher[28]則認為衰減系數應取10。在本文中，參考Semedo 等[30]取A=2，代入式（7）得到

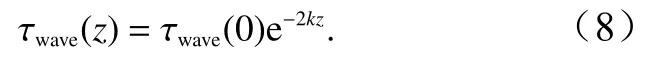
根據Belcher和Hunt[31]的推導結果，波浪的增長/衰減率β可以表示為

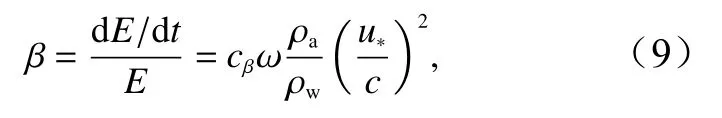
式中，E為海浪能量；cβ為波浪的增長/衰減率系數；u*為摩擦速度；c為波浪相速度。許多研究[31–33]一致認為cβ的取值在16～48范圍內，而具體取值在很大程度上取決于實際模型。在本文中我們根據涌浪條件 (c/u*> 20)，設置cβ=?35，此時式（8）變為

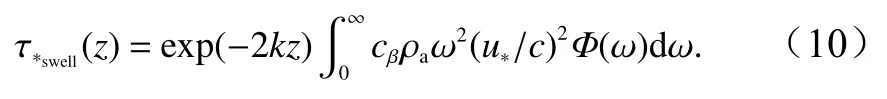
在涌浪的影響下，協譜會在與海浪同頻率區間產生明顯的峰值，據此可以通過對特定頻率區間積分提取出浪致雷諾應力，

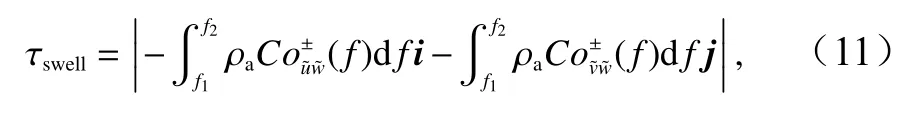
式中，f1和f2分別代表受涌浪影響的區間的上界和下界，且在該區間內，只取受涌浪影響的部分作為浪致雷諾應力，即當由涌浪引起的譜峰向上時，Co±取Co> 0的部分；當由涌浪引起的譜峰向下時，Co±取Co< 0的部分。

3 實測數據

本文使用的數據來自廣東茂名博賀海洋氣象觀測站，該平臺位于南海海域，經緯度為21°26.5′N，111°23.5′E，距離海岸線 6.5 km，平均水深約為 16 m，平臺的結構如圖1[14]所示。在鐵塔觀測中，我們在距平均海平面8 m、20 m、28 m和36 m處各安裝了一套渦相關觀測系統，包括超聲風速儀、CO2/H2O分析儀、紅外輻射儀和溫濕探頭等，用于測量3個方向的風速、超聲虛溫和水汽等脈動。除此之外，我們在海底布放了一套海浪觀測設備（AWAC；Nortek，Rud，Norway）用于觀測海浪和海流信息。

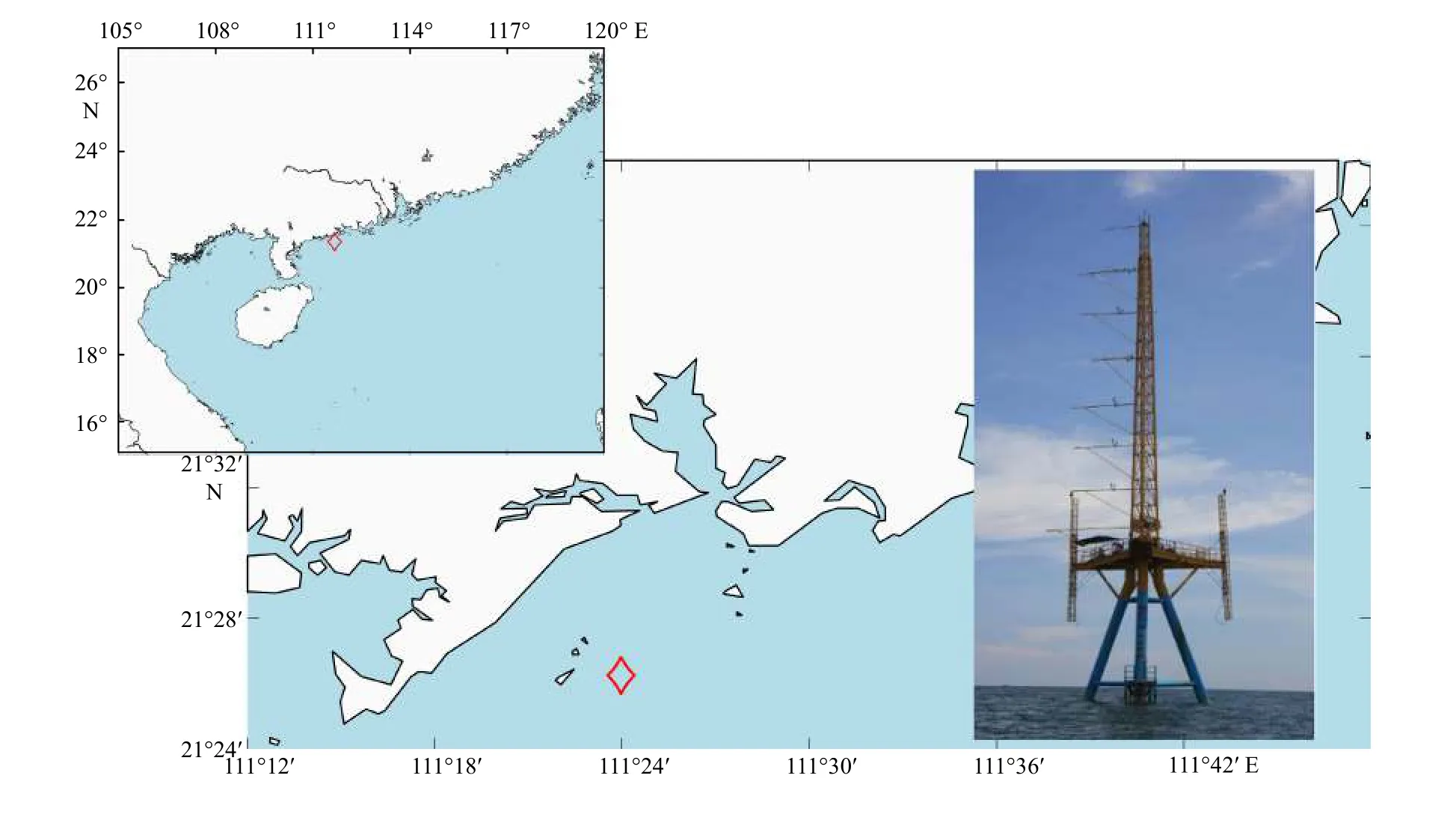
圖1 實測數據的平臺位置和結構[14]Fig. 1 Platform location and structure of measured data[14]

本文所使用的風速數據來自8 m高度的超聲風速儀，采樣頻率為20 Hz，朝向為正東。波浪數據來自海底的AWAC，該設備每3 h進行一次觀測，采樣頻率為1 Hz。湍流和波浪數據的時間均從2012年2月15日至5月8日。為確保數據的有效性，在分析數據之前我們對數據進行了預處理，包括去除野點、傾斜校正和去除趨勢[34]。

經過上述質量控制后，我們總共得到2 758個數據點，每個數據點以半小時為一個單元進行平均處理。圖2a給出了觀測期間風速、波齡隨著時間的變化，其中U8是8 m高度的平均風速，cp/U8代表波齡。由于摩擦速度u*會受到涌浪的影響，此處波齡采用cp/U8而非cp/u*。觀測期間大多數情況下風速小于10 m/s，處于低風速條件下。從波齡可以看出，觀測期間涌浪(cp/U8>1.2)占優，這為我們研究涌浪對大氣邊界層的影響提供了條件。圖2b給出了風向和浪向(本文中的風向定義為來向)隨時間的變化。風向從60°朝180°轉向，即由東北向逐漸轉為南向；浪向從120°朝180°轉向，即由東南向逐漸轉為南向。整體上，風向與浪向之間的差值約為30°。

圖2 距平均海平面8 m高度的風速和波齡cp/U8(a)，風向和浪向（b）Fig. 2 Wind speed at 8 m height above mean sea level and wave age (a),wind direction and wave direction (b)

4 結果分析

4.1 涌浪對邊界層的直觀影響

對觀測數據進行譜分析后，我們發現湍流譜在風浪和涌浪條件下的表現明顯不同。圖3a和圖3b分別給出了風浪條件下(3月8日9時)和涌浪條件下(4月9日10時)的湍流譜。從圖3b中可以看出涌浪存在時，湍流譜Suu、Svv和Sww在約0.1 Hz處都具有明顯的譜峰，這與前人的研究一致[18,35–36]。圖3b還顯示水平(u和v)和垂向(w)的譜峰大小不一致，其中Sww的峰值更加明顯。根據Miles[37]剪切不穩定理論：海浪可以激發3個方向的脈動但是不同方向的脈動隨高度的衰減系數不同，其中的衰減系數大而的衰減系數小。因此Sww的峰值比Suu和Svv更加明顯。值得一提的是，在該平臺上，Chen等[36]在海平面以上17 m處觀測到同樣的現象，表明涌浪誘導的脈動可以延伸到更高的高度。

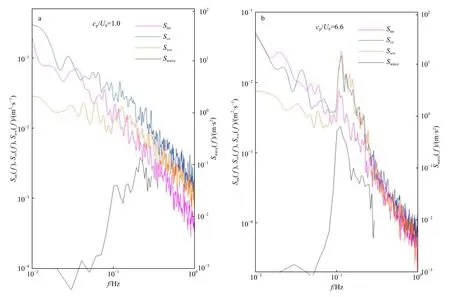
圖3 3個方向的湍流譜和海浪譜Fig. 3 Power spectra in three directions and directional wave spectrum

協譜給出了湍流通量在各個頻率上的分布。為了對比涌浪和風浪條件下動量通量的差異，圖4給出了順風向的協譜Couw和側風向的協譜Covw，其中圖4a和圖4c的時間與圖3a相同，圖4b和圖4d的時間與圖3b相同。圖4表明，在高頻部分(f>0.6 Hz)，協譜基本為0。此部分對應的湍流為慣性區間，該區間內湍流滿足局地各向同性，因此對動量通量的貢獻基本為0。在低頻部分(f<0.6 Hz)，協譜偏離零值。圖4a顯示風浪情況下的順風向的協譜Couw整體上為負值，表明湍流通量從大氣向海洋傳輸。與風浪情況不同，圖4b顯示涌浪情況下的協譜在0.1 Hz附近出現明顯的正值(紅色區域)，與圖3b的譜峰區對應，表示涌浪向大氣傳輸動量通量。圖4c顯示風浪情況下的側風向協譜Covw的正值與負值總體上均勻的分布在零值兩側；圖4d則顯示受涌浪影響，側風向協譜Covw出現了偏離零值的異常(紅色區域)。

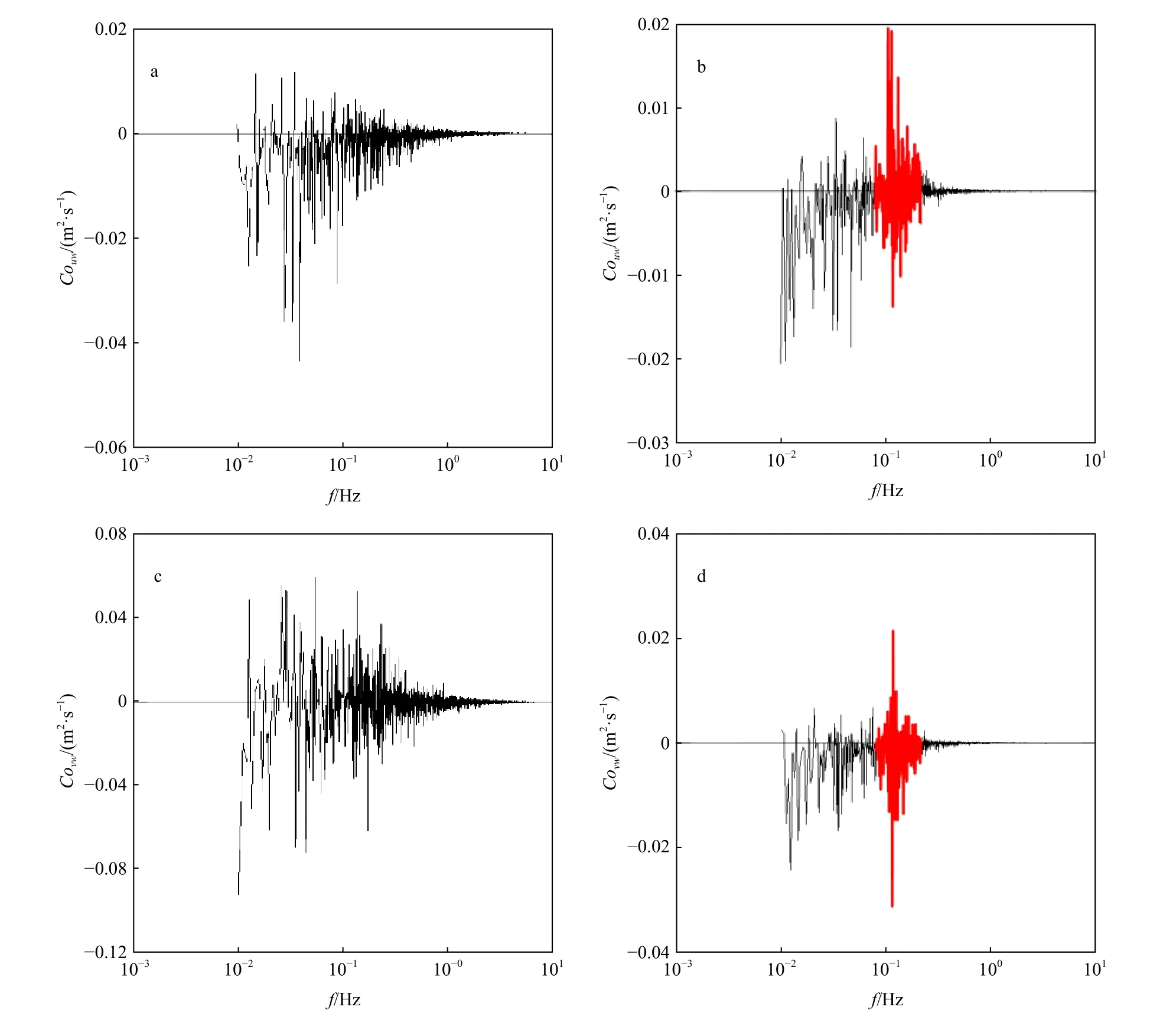
圖4 順風向（Couw）和側風向（Covw）的協譜Fig. 4 Along-wind (Couw) and cross-wind (Covw) cospectra

為了更好地分析涌浪對總應力的影響，圖5a和圖5b分別給出了風浪情況和涌浪情況下與圖4協譜相對應的Ogive曲線Ogx(綠色)和Ogy(藍色)。在風浪情況下，順風向的協譜Couw通常整體為負值，伴隨著一些隨機的正值。由式(4)可知，Ogx隨著頻率的減小整體上呈現遞減的趨勢，這與圖5a顯示的情況一致。由于風應力的偏向不同，側風向的協譜Covw正值和負值都是可能存在的，但其值比Couw小很多。因此Ogy的整體趨勢朝正或者朝負由實際的風向和浪向決定，其值比Ogx小很多。而涌浪情況下，如圖5b所示，Ogive曲線的整體趨勢與風浪情況一致，但在約0.1 Hz處產生突變，Ogx曲線突然增加，Ogy曲線急劇下降，分別對應協譜中譜峰向上(圖4b)和向下(圖4d)。這些特征與Zou等[14]的結果相似。但在實際情況中，Ogive曲線是突然增加還是急劇下降取決于浪向與風向的相對位置。浪向與風向小于90°時，順風向的協譜Couw譜峰向上，Ogx突然增加；浪向與風向大于90°時，順風向的協譜Couw譜峰向下，Ogx急劇下降。浪向在風向的右側時，側風向的協譜Covw譜峰向上，Ogy突然增加；浪向在風向的左側時，側風向的協譜Covw譜峰向下，Ogy急劇下降。

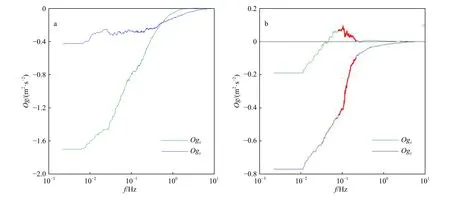
圖5 Ogive曲線Fig. 5 Ogive curve

4.2 浪致雷諾應力反轉符號時波齡的概率分布

圖4b顯示在涌浪情況下，涌浪會在譜峰處激發向上的動量通量，這意味著風從海浪中獲取能量，浪致雷諾應力為負。Zou等[14]的研究顯示，這種情況發生在風和涌浪的角度差小于90°時，圖4b和圖4d中風和涌浪的角度相差為77.4°，與Zou等[14]的結果相符。除此之外，Zou等[14]的研究還顯示，當風和涌浪的角度差大于90°時，涌浪反而從大氣中吸收能量，我們的研究結果中這種情況同樣存在。H?gstr?m等[22]的研究顯示上述兩種情況在風速為4.5 m/s時發生反轉。然而，考慮到海浪和邊界層的相互作用是一個復雜的過程，我們篩選了涌浪條件下浪致雷諾應力符號反轉(包括由正變負和由負變正兩個過程)時的數據，初步分析符號反轉時波齡的統計分布特征。

圖6a和圖6b分別展示了當順風向浪致雷諾應力和側風向浪致雷諾應力反轉符號時波齡的分布，其中橫坐標代表波齡的大小，縱坐標代表數據集中相對應波齡的統計個數。從中可以看出，圖6a和圖6b的統計結果基本服從正態分布，均值(臨界值)分別為80和60左右。因此分析可得，當cp/u*≈ 80時，在順風方向上浪致雷諾應力符號反轉的概率較大；當cp/u*≈ 60時，在側風方向上浪致雷諾應力符號反轉的概率較大。

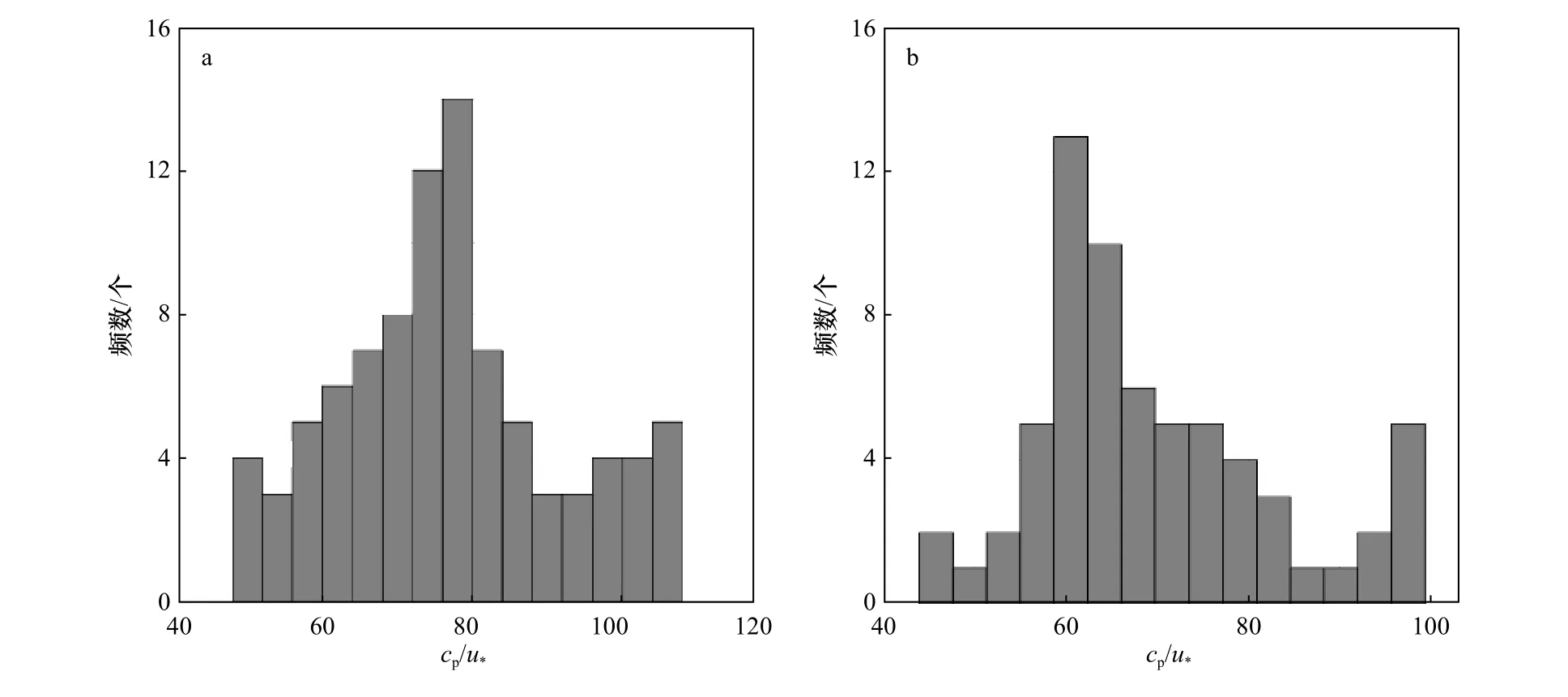
圖6 順風向（a）和側風向（b）浪致雷諾應力反轉符號時波齡的統計分布Fig. 6 Statistical distribution of wave age when wave-induced Reynolds stress reverses sign of along-wind (a) and cross-wind (b)

4.3 浪致雷諾應力

本節對比協譜法 (式（11）)與傳統方法 (式（10）)估算的浪致雷諾應力的差異，圖7中τswell為協譜法得到的浪致雷諾應力，τ*swell為傳統方法得到的浪致雷諾應力。計算結果顯示，τswell的大小基本在 10?4～10?2之間，τ*swell的大小基本在 10?7～10?4之間，整體上τswell比τ*swell大2～3個量級，這意味著式（10）可能顯著低估了浪致雷諾應力，浪致雷諾應力的傳統計算方法還有待改進。

為了更直觀地比較兩者之間的差異，我們將τ*swell放大500倍后再與τswell進行比較。如圖7所示，橫坐標為τswell的對數坐標，縱坐標為500τ*swell的對數坐標，藍點均勻分布在黑色直線的兩側，且通過計算得到此坐標系下τswell與τ*swell的相關系數為0.84，表明兩者相關性較強，這也從一定程度上說明基于協譜的估算方法是可靠的。

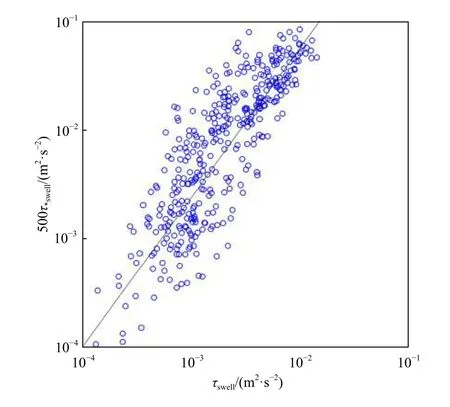
圖7 協譜法和傳統方法估算的浪致雷諾應力比較Fig. 7 Comparison of wave-induced Reynolds stress estimated by cospectrum method and traditional method

5 結論

本文基于中國南海茂名鐵塔上的實測數據，通過湍流譜研究了低風速涌浪條件下的海氣邊界層的湍流運動。分析結果表明，與風浪相比，在涌浪條件下3個方向的湍流譜Suu、Svv、Sww和波浪譜Swave在約0.1 Hz處都具有明顯的譜峰。除此之外，本文還給出了順風向的協譜Couw和側風向的協譜Covw的變化曲線。對比風浪，涌浪情況下Couw和Covw具有向上或向下的突出譜峰，對應于Ogive曲線突然上升或下降的階段。所有結果都表明，在某一頻率區間上，涌浪對大氣邊界層湍流有顯著影響。

浪致雷諾應力的正負與大小對海氣相互作用的研究具有重要意義。因此，本文統計了浪致雷諾應力符號反轉時的數據，研究了浪致雷諾應力的正負反轉時波齡的臨界值。結果表明，當cp/u*≈ 80時，在順風方向上浪致雷諾應力符號反轉的概率較大；當cp/u*≈ 60時，在側風方向上浪致雷諾應力符號反轉的概率較大。同時，我們還基于協譜法提取了浪致雷諾應力τswell，與傳統方法計算的浪致雷諾應力τ*swell做比較。結果表明，τswell與τ*swell的相關性較強，這從一定程度上說明基于協譜的估算方法是可靠的。但τswell的數值比τ*swell大2～3個量級，這意味著由傳統方法計算出的涌浪能量可能被大大低估了，傳統的浪致雷諾應力計算方法還有待改進。