因生而異 因地制宜
——大單元視角下“湊十法”教學的實踐探索

文|金 瀅 龔斌斌

一、“移植”之困：“十”之欲出，“湊”而不得

在一次單元整合教學的省級研討活動中，筆者偶遇別開生面的“湊十法”，心生向往，于是“移植”進自家課堂。奈何過程和結果卻與活動中的課堂大相徑庭，不如人意。

1.結果式表征抑制算理的生長。

關于“9+4”，學生選取小棒、畫圖和算式表征的典型進行交流、對比，但學生對“湊十”并沒有特別鮮明的需求和傾向。

2.模仿式遷移違背整合的初衷。

通過“9+4”的學習，引導學生用“湊十法”遷移計算“8+4”和“7+4”，學生情況如下：

二、刨根尋因：“學”之所需，法亦有別

1.他們的起點≠我們的起點。

隨著社會的發展，家長對于教育的期望和要求越來越高，但城鄉結合地區的家長大多還停留在知識技能培養的層面，把機械記憶結果作為計算學習的重點，很少會引導學生思考“為什么”。因此，我們的學生在算理的學習起點上相對要低一些。

2.位值的理解≠運算的理解。

對于一年級學生而言，對位值的“十”和運算產生的“十”還沒有很好地進行關聯，因此，對于為什么要“湊十”是迷茫的。

3.畫圖的經驗≠符號的經驗。

學生對于計算算理的表達能力有所欠缺，對于如何利用圖和式來表達自己的思考過程缺乏一定的經驗基礎，尤其是把圖和式進行主動地轉化更是難上加難。

三、“嫁接”修枝：縱覽全局，整合有度

單元教學整合絕非只是簡單地整合單元學習內容，整合的策略更不能簡單地加以“移植”，必須在精確掌握學生的學習起點基礎上，通過拓展、重構等策略，加工單元知識點，以促進學生理解算理，提高運算能力。

（一）鋪墊：特殊的“十”運籌帷幄

1.“格點”為媒，聯結數與運算。

10 以內數的認識，始終遵循的一條主線就是從“實物——橫向計數器——點子圖——抽象出數”，人教版在學習10 的加減法時，安排了這樣的方式展開，充分體現了點子圖在溝通算式和分合式之間的重要作用。其實，這是“湊十”的萌芽時刻，借這個起點，筆者又進一步設計了以下的“湊十”練習：

利用格子圖進行湊十，對應呈現加減法算式。通過系統學習，讓學生腦中有圖式，構建起10 的數模型，為“湊十法”計算做好準備。

2.意義渲染，感悟重要價值。

構建起10 的數模型后，還應該讓學生了解“十”的特殊性，比如借助教材的《你知道嗎》和繪本《古人是怎樣計數的》引領學生走進十進制的產生。在此基礎上，讓學生走進生活，去尋找生活中特殊的“10”，從數學回歸生活的過程中，學生發現原來“10”真的很特殊、很重要。

3.圖式轉換，愛上“10 加幾”。

“10 加幾”是學習了20 以內數的認識，掌握了20以內數的組成的基礎上進行學習的，它是將一個數“十幾”轉化為一個算式“10 加幾”的符號化變形，小棒直觀圖架設起兩者之間轉換的橋梁。但我們的教學并不能止于此處，更重要的是，讓學生經歷在例題學習的基礎上創造出10 加幾的算式，同時通過有序思考、對比觀察，發現“10 加幾等于十幾”這一重要規律，感受到計算的便捷，讓學生愛上“10 加幾”。

（二）構序：運算的“十”多邊共識

?

1.切換慢鏡頭，“倒逼”算理絲絲入扣。

運算方法可以通過簡單的模仿進行學習，而運算能力的形成則必須依賴對算理的理解。筆者試著將原設計里利用“9 加幾”的計算教學來理解“湊十法”的過程改為“串聯”的呈現方式，層層深入，逐層對比。讓學生在整個方法優化和溝通的過程中，感受到“湊十”思維對進位加法計算的必要性。

（1）動態演繹，定格“跳躍式”思維。

美國學者富森將表內加法進行劃分，不進位的是“單一單位概念結構”，進位的是“多單位概念結構”。對于后者，通過前測可以發現，學生有兩種水平：轉換為單一單位概念結構，也就是接著數；另一種就是轉化成相對獨立的兩個單位，也就是直接“湊十”。因此，先借助半抽象的小棒來實現水平一到水平二過渡。

師：你知道9 加4 等于幾嗎？

師：看來大家都已經知道9 加4 的結果了，那么這個結果是怎么得來的呢？老師為大家準備了一些小棒，請大家借助小棒，擺一擺9 加4 得到13 的計算過程。

對比小結：第三種方法是先得到了10，再與3 合并得到13，我們一眼就看出來了。再通過關鍵問題“為什么只移動1 根”思考湊十的另一個核心要素。

（2）格點再現，喚醒“湊十”經驗。

利用點子圖解釋讓學生在頭腦中主動喚起先前建立的10 的模型結構。

師：剛剛大家用小棒擺出了9 加4 等于13 的計算過程，如果用小圓圈來畫一畫，畫出9 加4 等于13的計算過程，你們能做到嗎？

對比小結：第三種方法，我們不但能看出是9 加4，還圈出了10，讓我們一眼就看出13。

（3）符號表征，實現算理內化。

在直觀積累的基礎上，用算式進行表征，就是符號化表征的進階學習，符號化的過程本就是抽象的過程，抽象水平越高，可遷移的可能性就越大。

師：老師如果要你們用寫算式的方法，寫出9 加4 等于13 的計算過程，你們還能做到嗎？

對比小結：第三種方法我們不但看到了9 加1 得到10 的過程，我們還能清楚地看出1 是從4 里面分出來的，而且還剩下3，這樣10 和3 相加就馬上得到13 了。

最后通過讓學生同桌交流，對9+4 的三次表征方法異中求同，引導學生發現，無論是小棒、點子圖還是算式，都經歷了從4 里面拿出1，和9 組成10，10 再與3 合并得到13，“湊十法”一詞的出現水到渠成。

2.推進快鏡頭，遷移算理步步為營。

（1）似曾相識再湊十。

第二環節選擇一個與9 接近的8 先進行遷移，就是要培養學生具備有意識“湊十”到自主遷移的能力，讓學生在微妙的變化中，感受到同中有異、異中有同，跳出“把9 湊十”、“用1 湊十”的思維框架。

師：同學們，9+8 你們已經會算了，老師現在要將這個算式變一變，你還會嗎？請你在《學習單》上記錄你的計算過程與想法。

師：都是8+9=17，過程有什么不一樣？

通過交流發現，8+2=10，從第二個加數中拿出幾去湊十，要看另一個加數是多少。

（2）不同角度找本質。

同一道題既可以把前一個加數湊成十，也可以把后一個加數湊成十，通過對比可以加深算理，同時再次體會8 和9 湊十過程是不同的，為后面學習小數加大數時的靈活選擇方法做準備。

師：這兩種方法又有什么相同和不同的地方？

對比小結：我們不僅可以將第一個加數湊成10，還可以將第二個加數湊成10。不管怎么樣，我們在計算這類加法時，都是先想“湊十”再計算的。

（3）觸類旁通想轉化。

6、5、4、3、2 加幾的計算雖然也可以轉化為10 加幾，但加數與10 相差越來越大，“湊十”的過程也越來越復雜。因而，需要在枚舉的基礎上，讓學生自主地聯想到將小數加大數轉化為大數加小數。

師：那么如果在計算中出現了7、6、5、4、3、2，也可以通過先湊“十”來計算嗎？

要求：請你自己編兩道結果是20 以內，計算過程中需要用到“湊十”想法的算式，并把你的計算過程清楚地記錄下來。

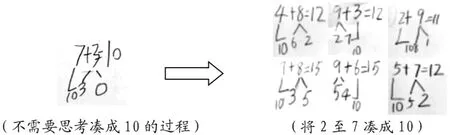
師：在計算的時候有什么相同的地方？

小結：當我們想好了要把其中一個加數湊成10，就只要想另一個加數需要分出幾、還剩下幾，這樣就可以很快得到計算的過程和結果了。

師：為什么都是湊成十，而沒有湊成其他數？（10加幾最方便——湊十的意義完美流露）

師：這兩位同學計算同一道算式，你更喜歡選擇哪種方法？

小結：當我們遇到小數加大數時，可以聯想大數加小數得到結果。

（三）融通：高階的“十”細致深刻

數學學習的結構化有助于提高學生的學習能力，在教學時將相應的算式歸類比較，有助于學生發現計算中的規律，將隱藏其中的算理進一步挖掘，在推理過程中進一步感悟湊十背后的秘密，提升計算的速度。

1.縱向勾連，歸納和演繹中整合運算。

師：結果是20 以內需要思考“湊十”的算式還有很多，老師將其中的一些整理在一張表格中。你能發現9 加幾的算式有什么規律嗎？得數有什么特點？得數和第二個加數有怎樣的聯系？

通過交流學生逐漸發現其中的規律：得數都是十幾，得數個位上的數比第二個加數少1。

師：十幾中的10 從哪兒來的？為什么每個得數的個位比第二個加數小1？

引導學生結合算理來分析，通過這樣的有序列舉、觀察比較、分析歸納，學生概括出“湊十減一”的簡化思考過程的方法，將分解的思維動作整合為算法模塊，提高計算的速度和正確率。

2.橫向勾連，類比和演繹中整合運算。

利用9 加幾的規律，讓學生進一步有序填寫空格中的算式，并繼續觀察剩余的幾列算式中蘊藏的規律。有序的學習素材能較好地提高學生的觀察能力和分析能力，促進學生有效地展開探索活動。這里，既可以依次進行分析，也可以通過9 加幾推理分析，并通過核心問題“為什么8 加幾是湊十減二，7 加幾是湊十減三”促使學生在類比推理的驗證過程中回歸“湊十法”的算理本質，提升運算能力，發展推理能力。