類(lèi)比一次函數(shù) 生長(zhǎng)二次函數(shù)
文/曹曉榮
我們知道,形如y=kx+b(k≠0,k、b為常數(shù))的函數(shù)叫作一次函數(shù),它右邊是一次式,稱(chēng)為一次函數(shù)是“名副其實(shí)”的。由此我們聯(lián)想到將右邊換為二次式,得到另一個(gè)“名副其實(shí)”的函數(shù)新成員——二次函數(shù),即形如y=ax2+bx+c(a≠0,a、b、c是常數(shù))的函數(shù)叫作二次函數(shù)。掌握函數(shù)表達(dá)式與代數(shù)式之間的這種聯(lián)系,有助于我們理解二次函數(shù)的概念。
與學(xué)習(xí)一次函數(shù)的路徑一樣,我們學(xué)習(xí)二次函數(shù)的路徑便是這樣的。
一、引入概念
從熟悉的、簡(jiǎn)單的實(shí)際問(wèn)題出發(fā),通過(guò)問(wèn)題中的數(shù)量關(guān)系引入二次函數(shù)的概念,感受二次函數(shù)與生活實(shí)際的密切聯(lián)系,既揭示生活與數(shù)學(xué)的聯(lián)系,又體現(xiàn)教材前后呼應(yīng)的整體性。
學(xué)習(xí)一次函數(shù)概念的時(shí)候我們?cè)?jiàn)過(guò)“水滴激起的波紋”這幅圖片。二次函數(shù)概念的引入也用了這幅圖片,只不過(guò)我們關(guān)注的焦點(diǎn)由“不斷向外擴(kuò)展的圓的周長(zhǎng)是該圓半徑的函數(shù)”,轉(zhuǎn)為“圓的面積是該圓半徑的函數(shù)”,即C=2πr和S=2πr2。我們通過(guò)研究?jī)蓚€(gè)函數(shù)表達(dá)式的差異引出二次函數(shù)的概念,然后再通過(guò)問(wèn)題來(lái)進(jìn)一步理解二次函數(shù)的概念。
問(wèn)題1 下列一定是二次函數(shù)的是()。
A.y=2x2B.y=2x-1
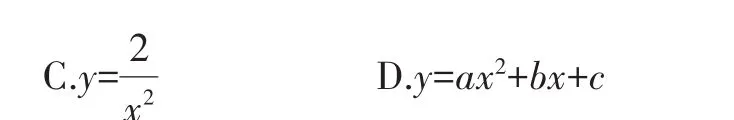
問(wèn)題2 已知二次函數(shù)y=x2-5x+3,則二次項(xiàng)是______,一次項(xiàng)系數(shù)是______,常數(shù)項(xiàng)是______。
問(wèn)題3 已知函數(shù)y=(m2-m)x2+(m-1)x+m+2。當(dāng)m滿(mǎn)足______時(shí),這個(gè)函數(shù)是一次函數(shù);當(dāng)m滿(mǎn)足______時(shí),這個(gè)函數(shù)是二次函數(shù)。
通過(guò)問(wèn)題進(jìn)一步認(rèn)識(shí)二次函數(shù)表達(dá)式的特征:
(1)函數(shù)表達(dá)式是二次整式;
(2)二次項(xiàng)系數(shù)不能為0;
(3)自變量的最高次數(shù)為2次。
二、研究圖像與性質(zhì)
研究一次函數(shù)是從列表、描點(diǎn)、連線(xiàn)開(kāi)始,觀察、發(fā)現(xiàn)圖像和性質(zhì),那么研究二次函數(shù)的圖像和性質(zhì)我們分三步走:從1開(kāi)始→從1 到一切→一切從a開(kāi)始。由特殊到一般,運(yùn)用數(shù)形結(jié)合的思想探索二次函數(shù)的圖像和基本性質(zhì)。
從1開(kāi)始——y=x2
通過(guò)描點(diǎn)法用平滑的曲線(xiàn)(類(lèi)比反比例函數(shù)圖像畫(huà)法)畫(huà)出y=x2的圖像。
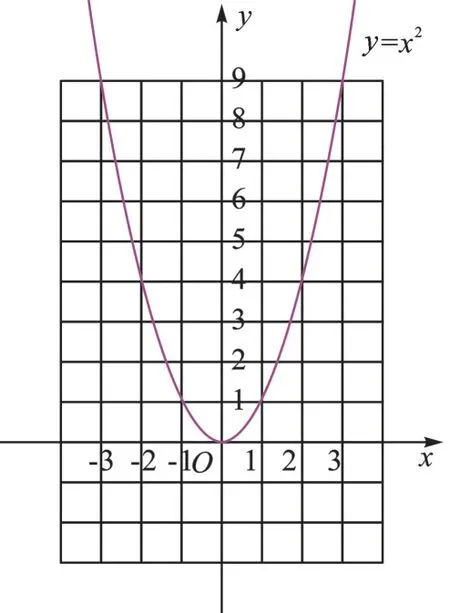
觀察圖像,初步得出圖像的特征:
形狀:U型;
對(duì)稱(chēng)性:關(guān)于y軸對(duì)稱(chēng);
圖像趨勢(shì):先下降后上升;
最值:最低點(diǎn)為(0,0),當(dāng)x=0 時(shí),y的最小值為0。
由此了解拋物線(xiàn)及拋物線(xiàn)的頂點(diǎn)、對(duì)稱(chēng)軸等。
從1到一切——y=ax2(a≠0)


一切從a開(kāi)始——y=ax2+bx+c(a≠0)

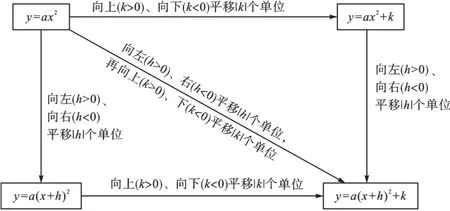
二次函數(shù)圖像平移小口訣:上下平移在末梢,左右平移在括號(hào);上加下減,左加右減。
三、類(lèi)比學(xué)習(xí)
從函數(shù)的視角出發(fā),審視一元二次方程與二次函數(shù)的關(guān)系,借助圖像的直觀性,探索使函數(shù)值y為0 時(shí)自變量x的值,進(jìn)而得到用二次函數(shù)的圖像求一元二次方程近似解的方法,領(lǐng)悟無(wú)限逼近的重要思想方法。
二次函數(shù)y=ax2+bx+c(a≠0)的圖像與x軸的交點(diǎn)的橫坐標(biāo)是一元二次方程ax2+bx+c=0(a≠0)的實(shí)數(shù)根,函數(shù)圖像與x軸的交點(diǎn)情況可由對(duì)應(yīng)方程的根的判別式b2-4ac與0 的關(guān)系來(lái)判斷。用二次函數(shù)y=ax2+bx+c(a≠0)的圖像估計(jì)一元二次方程ax2+bx+c=0(a≠0)的根時(shí),一元二次方程的根就是二次函數(shù)圖像與x軸的交點(diǎn)的橫坐標(biāo)的值。
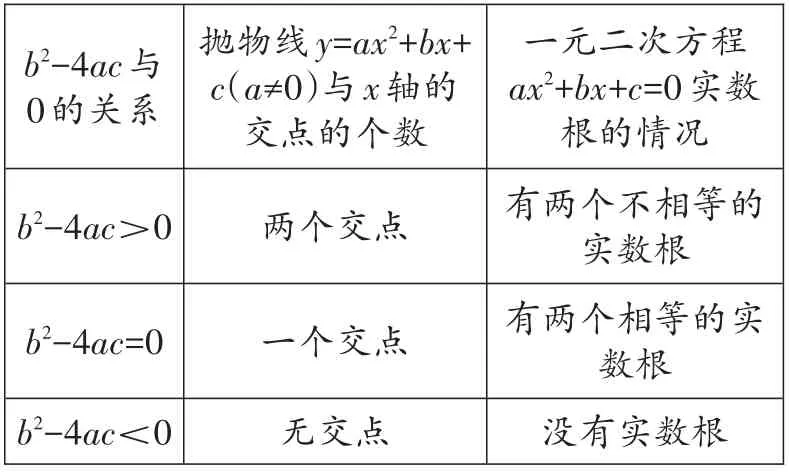
b2-4ac與0的關(guān)系b2-4ac>0拋物線(xiàn)y=ax2+bx+c(a≠0)與x軸的_____________交點(diǎn)的個(gè)數(shù)兩個(gè)交點(diǎn)b2-4ac=0 b2-4ac<0______一個(gè)交點(diǎn)無(wú)交點(diǎn)________一元二次方程ax2+bx+c=0實(shí)數(shù)根的情況____有兩個(gè)不相等的實(shí)數(shù)根_____有兩個(gè)相等的實(shí)數(shù)根______沒(méi)有實(shí)數(shù)根___
拋物線(xiàn)y=ax2+bx+c(a≠0)與直線(xiàn)y=kx+m相交于點(diǎn)M(x1,y1),N(x2,y2)(x1<x2),當(dāng)a>0 時(shí),不等式ax2+bx+c>kx+m的解集是x<x1或x>x2,不等式ax2+bx+c<kx+m的解集是x1<x<x2;當(dāng)a<0 時(shí),不等式ax2+bx+c>kx+m的解集是x1<x<x2,不等式ax2+bx+c<kx+m的解集是x<x1或x>x2。
進(jìn)一步思考,由二次函數(shù)y=ax2+bx+c(a≠0)的函數(shù)值y>0(或y<0),即可得到一元二次不等式ax2+bx+c>0(或ax2+bx+c<0),此時(shí)確定不等式的解集就轉(zhuǎn)化為求拋物線(xiàn)位于x軸上方(或下方)時(shí)對(duì)應(yīng)點(diǎn)的橫坐標(biāo)的取值范圍。如拋物線(xiàn)y=x2+4x-5 位于x軸上方時(shí)對(duì)應(yīng)點(diǎn)的橫坐標(biāo)的取值范圍是x<-5 或x>1,則不等式x2+4x-5>0的解集是x<-5或x>1。
問(wèn)題 若二次函數(shù)y=x2-4x+n的圖像與x軸只有一個(gè)公共點(diǎn),則n________。
【解析】與x軸只有一個(gè)公共點(diǎn),則b2-4ac=0,可得n=4。
變式1 若二次函數(shù)y=x2-4x+n的圖像與坐標(biāo)軸只有一個(gè)公共點(diǎn),則n________。
【解析】由題意知圖像與x軸沒(méi)有公共點(diǎn),則b2-4ac<0,可得n>4。
變式2 若二次函數(shù)y=x2-4x+n的圖像與坐標(biāo)軸有兩個(gè)公共點(diǎn),則n________。
【解析】由題意知圖像與x軸只有一個(gè)公共點(diǎn),則b2-4ac=0,可得n=4;當(dāng)n=0 時(shí),圖像過(guò)原點(diǎn),則其與坐標(biāo)軸有兩個(gè)交點(diǎn),所以n為0或4。
變式3 若函數(shù)y=nx2-4x+1 的圖像與坐標(biāo)軸有兩個(gè)公共點(diǎn),則n________。
【解析】當(dāng)n≠0時(shí),圖像與x軸只有一個(gè)公共點(diǎn),則b2-4ac=0,可得n=4;當(dāng)n=0 時(shí),一次函數(shù)y=-4x+1與坐標(biāo)軸有兩個(gè)公共點(diǎn),所以n=0或4。
變式4 若二次函數(shù)y=x2-4x+n的圖像與坐標(biāo)軸有三個(gè)公共點(diǎn),則n________。
【解析】圖像開(kāi)口向上且與坐標(biāo)軸有三個(gè)交點(diǎn),則圖像一定與x軸有兩個(gè)交點(diǎn)且不過(guò)坐標(biāo)原點(diǎn),由Δ>0且n≠0可得n<4且n≠0。
變式5 若函數(shù)y=nx2-4x+1 的圖像與坐標(biāo)軸有三個(gè)公共點(diǎn),則n________。
【解析】當(dāng)n=0 時(shí),一次函數(shù)y=-4x+1 與坐標(biāo)軸只有兩個(gè)公共點(diǎn),不符題意,所以當(dāng)n≠0 時(shí),圖像一定要與x軸有兩個(gè)交點(diǎn),由Δ>0且n≠0可得n<4且n≠0。
我們通過(guò)類(lèi)比學(xué)習(xí),可以了解知識(shí)的發(fā)生、發(fā)展過(guò)程,找到學(xué)習(xí)函數(shù)的通法,不僅能在學(xué)習(xí)二次函數(shù)的過(guò)程中理順?biāo)悸罚魑P(guān)系,深化理解,還能為以后的函數(shù)學(xué)習(xí)奠定基礎(chǔ)。

