動手做數學
——單元整合下的計算教學實踐

◎錢一波 （太倉市港城小學，江蘇 蘇州 215400）

學生學習知識不是靠模仿來學習，也不是通過做大量的練習或者死記硬背來學習．教師是學生的引導者，要主動給學生設計教學活動，營造一個能夠操作的環境，讓學生在實際動手操作中感知數學知識的趣味性，有一個很好的情感體驗，掌握相關知識，并且能夠解決生活中的實際問題．教師要為學生創造出這樣一個適合的環境，使其經歷必要的過程，這對于提高學生的邏輯能力有很大的幫助．學具作為獲得知識的橋梁，在教學過程中是不可或缺的一部分，學生主動操作與思考，在實際動手操作過程中體驗數學的有趣．

一、學生學習情況現狀分析

在小學階段，學生從認讀寫數開始，再到之后的運算，這個過程都離不開形象具體的實物．在現代化的課堂教學中，教師會通過現代教育技術手段進行課堂教學，這樣更加直觀形象．但是這樣也會存在一些局限性．如只是讓學生觀看教學視頻，而忽視了學生自己動手操作，這樣會降低教學質量，學生成了觀眾，不再是課堂的主體，不利于學生更好地獲得知識．我們都知道數學學習最基礎的就是數的運算，我們也可以從小學數學教科書內容結構表中看到數的運算貫穿于12 冊教材，包括口算、筆算、混合運算、運用運算律進行簡便計算等，其中豎式計算屬于程序性知識，教師若灌輸式地教學，容易陷入教學誤區，缺少計算算理的支持和學生自身的操作體驗，難以使教學與學生已有的知識水平相聯系．年級越低的學生在教學中越應該多多動手操作，所以，在每一次教學活動中，教師都要給學生更多的動手操作的機會，學生自己操作學具，從中獲得知識，掌握基本技巧．

二、基于教材開展單元整合

以“加法筆算”為例，對比不同版本的教材，人教版在一年級下冊安排了“100 以內的加減法”，分為口算和筆算兩部分，先是教學兩位數加減一位數和整十數的口算；蘇教版教材亦是如此．但人教版教材后面緊跟著兩位數加兩位數、兩位數減兩位數，以及連加、連減、加減混合，而蘇教版教材為了合理分解教學目標，分散教學難點，在一年級下冊第四單元安排了100 以內的不進位加法和不退位減法，第六單元安排了100 以內的進位加法和退位減法，在二年級上冊第一單元又安排了100 以內的連加、連減和加減混合，利用分豎式或連豎式進行加、減兩步計算，在二年級下冊第六單元安排了三位數的加法計算，這是在兩位數加法筆算的基礎上安排的，小學階段整數加法的教學要在本單元全部完成．從兩位數加法到三位數加法，原來的計算經驗可以在新的計算范圍內繼續應用．這樣安排看起來無可厚非，但學生在算法的理解方面沒有得到更多的體驗，教師馬上教學生學習豎式計算對學生來講會感覺很難．面對這樣一個問題，筆者有一個大膽的想法，就是對教材進行重組．整合的方式如表1所示．分三課時教學，第一課時運用學具進行計算，讓學生初步獲得經驗；第二課時圖示與豎式相結合，這樣就變得通俗易懂；第三課時其實就是拓展創造，靈活運用．

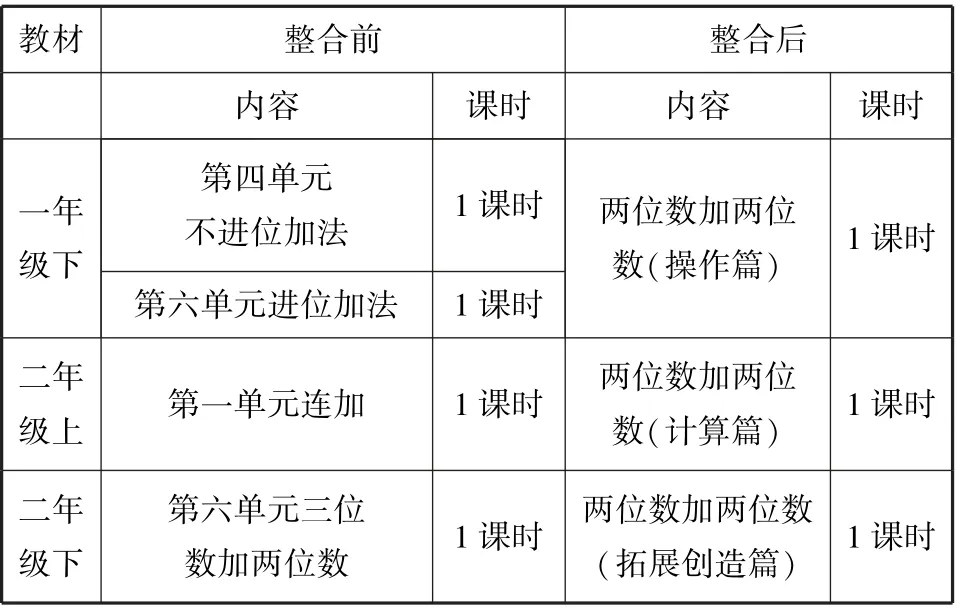
表1 “兩位數加兩位數的筆算”單元整合教學結構調整表

（一）單元整合的依據

整合是指通過協調和整合將分布的元素結合起來，這主要體現在教材的重組上．為了更好地讓學生將所學的知識整合起來，我們可以對教學的內容順序進行調整，把內容合并或增加部分內容，或改變教師的教學方式等．

1．學生學習經驗的需要

筆者通過對個別孩子的訪談發現，學生對于為什么這樣列豎式不是很清楚，對豎式計算規定背后的道理也不知道．單元整合教學可以完善學生的現有經驗，讓學生更加深刻地理解規定背后的道理．

2．打通教材編排的需要

學生對豎式計算中的算理不是很容易理解，算理教學是計算教學的重點以及難點，但不管兩位數加兩位數還是兩、三位數加法，算理都是互通的，所以單元整合教學可以有效利用這一點，使學生舉一反三，有利于學生學習經驗的遷移．

3．實現自我生長的需要

在豎式的規定上，教師的教學過程非常生硬，學生在學習的過程中也很死板．產生這樣的問題就在于它是被割裂出來的一個獨立的空間，缺少學生的操作與體驗，與學生的現有水平很難有聯系．在單元整合教學活動中，教師可以抓住這一點，讓學生操作學具，在活動中交流討論，對比得出結論．

（二）單元整合后的教學目標

在充分理解了教學內容、了解過學生學情之后，筆者將兩位數加兩位數的筆算教學內容進行了單元整合，確定了每課時的教學目標（如表2）．

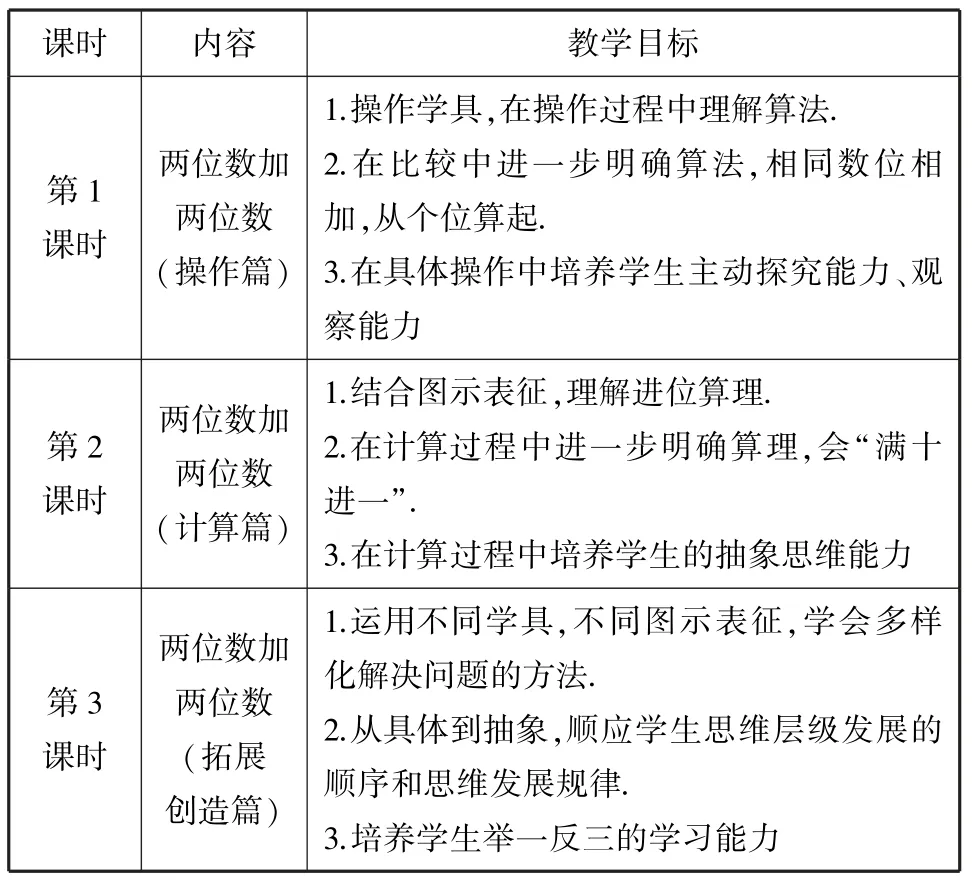
表2 “兩位數加兩位數的筆算”單元教學目標

（三）單元整合的教學實踐

1．方塊計算，建立表象

（1）用方塊計算45＋23（不進位）

由于有些學生在學前的基礎相對較好，這些學生對于不進位計算已經具有了一定的水平，有自己的思維方式．這部分學生可以更容易地激發起另一部分學生的主動探究欲望．教師通過提問的方式，讓學生動手操作進行驗證通過討論以及教師評價，學生得出兩種方法（如圖1所示）：

圖1

方法一：將4 根和2 根放一起，一共6 根；5 塊和3 塊合起來，一共8 塊，所以是68．

方法二：先把5 塊和3 塊合起來，是8 塊，再把4 根和2根合起來，是6 根，也是68．

教師提醒學生比較兩種方法的相同點和不同點，得出結論：不管哪種方法，都是相同數位相加，十位和十位相加，個位和個位相加，而且最后結果也相同，但過程有所不同．方法一先算條狀總數再算塊狀總數，而方法二先算塊狀總數再算條狀總數，由于是不進位加法，所以不管哪種方法都比較方便計算，這一比較為后面怎樣計算更簡便埋下伏筆．

（2）方塊計算45＋28（進位）

有了第一次的操作活動經驗，學生興趣更高，操作起來速度更快．此時會出現兩種方法：

方法一：如圖2所示，①把4 根和2 根合起來，是6 根；

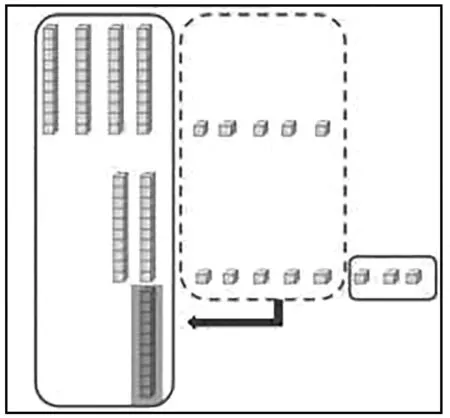
圖2

②把5 塊和8 塊合起來，滿10 塊拼成1 根，還多3 塊；

③6 根和拼成的1 根一共是7 根；

④7 根和3 塊合起來，一共是73．

方法二：如圖3所示，①把5 塊和8 塊合起來，滿10 塊可以拼成1 根，還多3 塊；

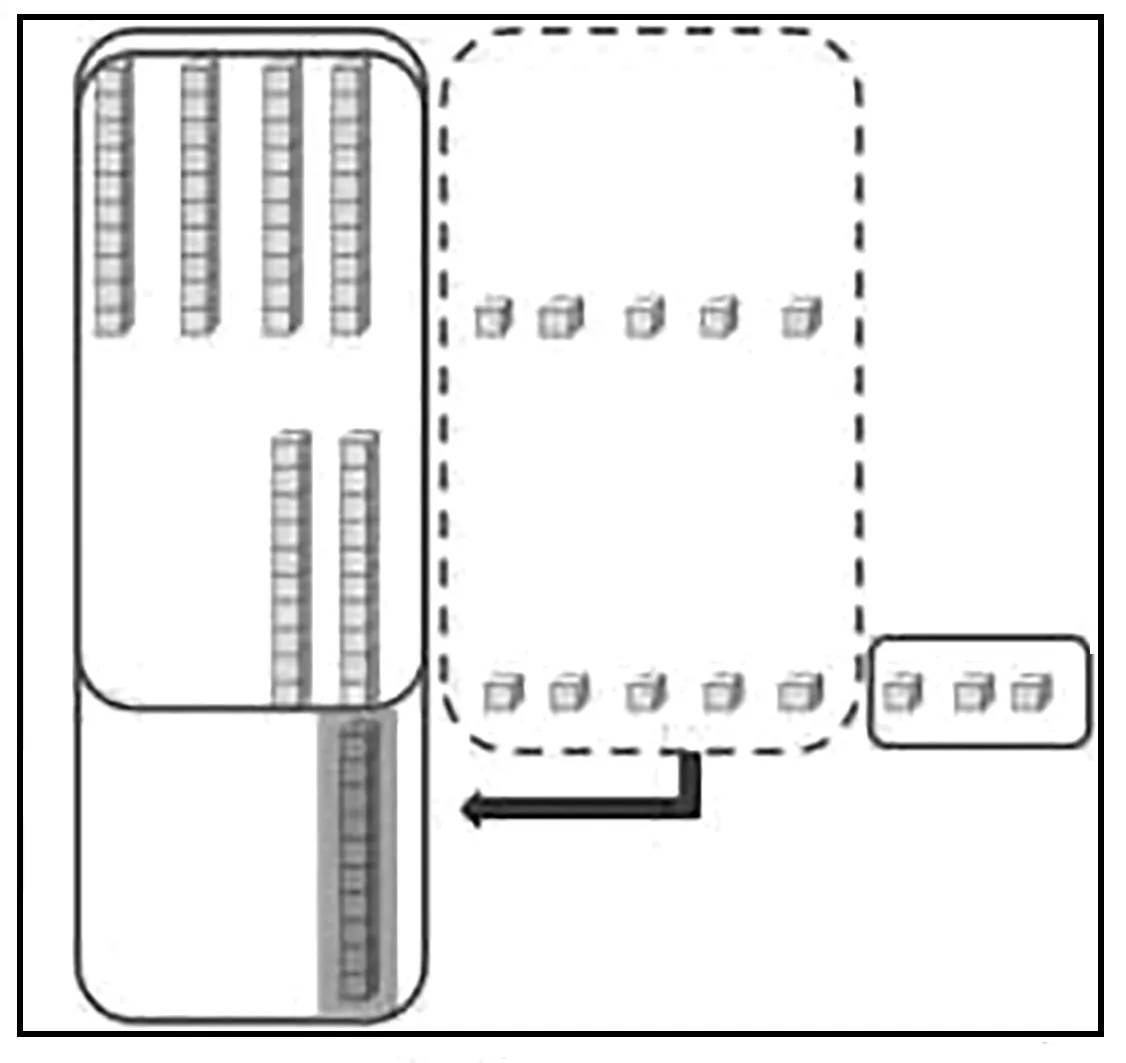
圖3

②4 根和2 根和新拼成的1 根合起來，一共7 根；

③7 根和3 塊合起來，一共是73．

教師追問：“回想一下兩種計算方法，哪種更方便些？”此時學生就會發現先算十位用了4 步，先算個位只用了3步，自然而然發現先算個位更方便，算法就自然引出．

（3）例題3：34＋16＝？

此前計算了不進位和進位的算式，所以這道例題就是整十數的計算，教師提問：“你能用更簡便的計算方法擺一擺、算一算嗎？”學生在計算時，就會將相同數位相加，先算個位，再算十位，最后得出得數（如圖4所示）．

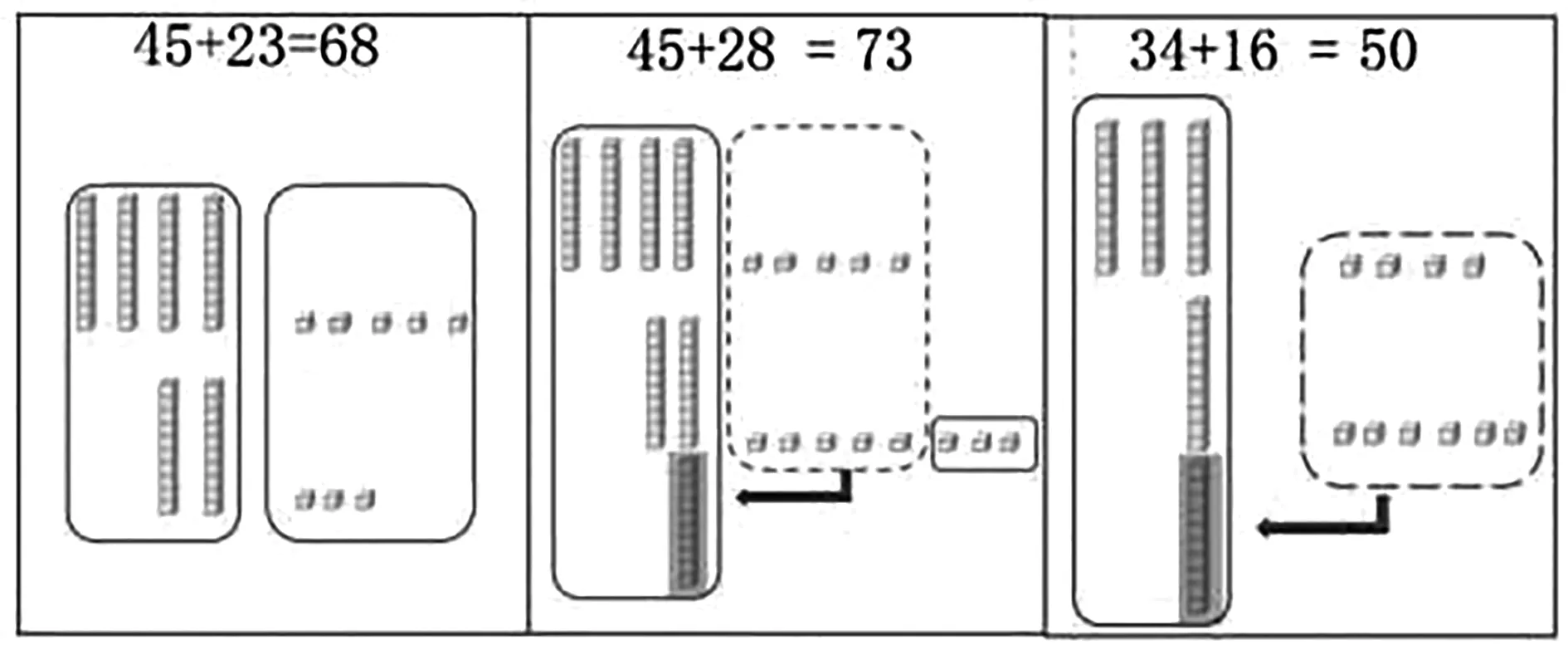
圖4

這一環節的教學意圖在于引領學生初步感知計算的順序．通過比較，學生發現相同數位相加，先算個位更方便．在擺方塊的過程中很自然地呈現了算法．

2．結合圖示，理解算理

此時學生通過自己的親手操作，有了一定的經驗，教師可以減少學具，在具體形象思維和抽象邏輯思維之間慢慢過渡．所以接下來我們運用圖示進行計算．

如圖5所示，1 根代表10，34 里面有3 個10，所以畫3根，1 個正方形代表1，4 里面有4 個1，所以畫4 塊．接著畫16，16 是1 個10 和6 個1 組成的．

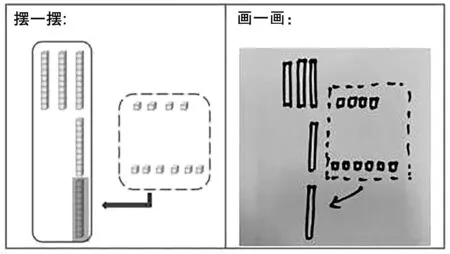
圖5

在理解算理時，教師通過圖示來引導學生理解橫式、豎式與方塊圖，讓學生從中體會它們之間的演變過程，探究“兩位數加兩位數”的算理．例如34＋16 這道題，如圖6所示．個位上4＋6 是零散著相加，變成1 根，即10 個1 就是1 個10，十位上3＋1 就是3 根加1 根，10 個方塊又拼成了1 根，即表示進位一，合起來一共5 根，即50．教師通過教學圖片，進一步讓學生理解“滿十進一”．在學生自主探索交流的教學環節中，教師要再一次結合方塊圖進行一一對應，使學生理解其中的原理．

圖6

特別要注意的是，在教學“整數筆算加法”的過程中，教師要指導學生理解其中的原理與算法，其過程不宜過快．在教學計算的過程中，算理是非常重要的環節，是算法的理論基礎所在的關鍵，在計算過程中，僅僅依靠學具是很難實現的．在教學活動中，圖示與豎式的雙重結合，就很好地解決了這個問題．

3．創造拓展，舉一反三

第3 課時是在前兩節課的基礎上進行的拓展遷移．眾所周知，在數學教學中，我們不僅要讓學生學會學習，而且要鼓勵他們去創新，不斷發現問題，提出問題，培養學生的學習能力，讓學生創造性地學習．

這一課時，教師可以讓學生運用不同學具、不同圖示進行拓展創造，如圖7所示，可以把方塊換成其他學具，如小棒．我們沿用口算的教學方法，生動形象地表示出什么是進位．通過撥算珠來計數，學生可以更加直觀地知道“滿十進一”．

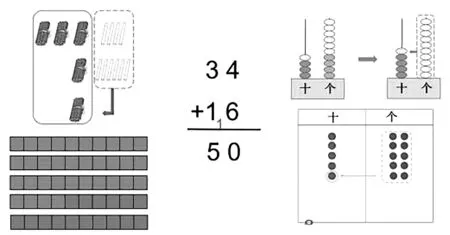
圖7

操作過程與學生的思維聯系起來，創新意識就在動手操作中不斷萌發．教師可以鼓勵學生進行同桌或小組合作，引導學生在合作學習的過程中通過觀察、猜想、歸納、類比、聯想等思想方法，主動地發現問題和提出問題．教師像這樣采用多種方式教學，不僅可以使教學課堂多樣化，還可以很好地進行教學過渡，有利于教學結構化，并且順應了學生的發展規律．教師可以讓學生運用所學知識計算連加，舉一反三．這樣利用了3 課時進行加法筆算的單元教學，教師還可以利用3 課時進行減法筆算的單元教學實踐，學生有了加法筆算的經驗之后，可以直接將其遷移到減法筆算的學習中．

總之，教師是環境的創設者，自由開放的課堂空間使學生保持愉快的學習心境，適當引導學生操作學具是必不可少的環節．學生在親身實踐中體驗數學，體驗多種教學方式，把課堂轉化成學生的主場．這樣學生有了學習的欲望，掌握的知識也會比較牢固，印象更加深刻，從而使課堂上的教學效果加倍．