對一類圓錐曲線定值問題的探究

江蘇省南通市海門證大中學 (226100) 周雅俊

平面解析幾何在《普通高中數學課程標準(2017年版2020年修訂)》中放入幾何與代數主題中，核心思想是以代數的方法解決幾何問題，重點提升學生的直觀想象、數學運算、數學建模、邏輯推理和數學抽象的數學核心素養.教師在教學時要引導學生多角度地研究問題、多層次地探究問題，達到做一道會一類，促進學生的數學核心素養的提升.筆者在與學生一起解題時，和學生一起發現了一類圓錐曲線的定值問題的一些性質，整理成文.本文僅以焦點在x軸上的圓錐曲線加以說明，僅作拋磚引玉，期待得到大家的指點.

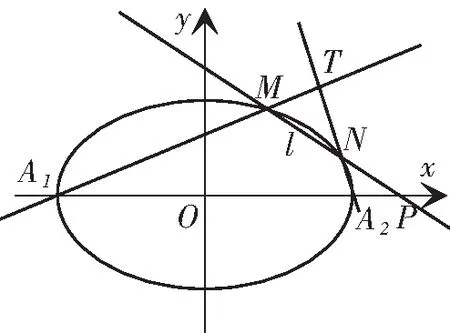
圖1

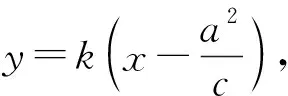
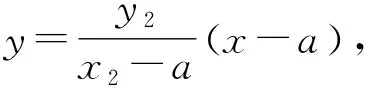
性質1中是過右準線與x軸的交點作一條直線，得出交點T的橫坐標為定值.類似的可以過橢圓的右焦點作一條直線，于是得到如下性質.

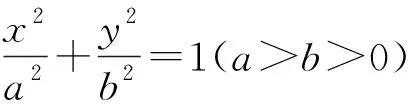
同為有心二次曲線,雙曲線也具有相似的性質，進一步探究發現了以下的性質.

圖2

性質2、3、4的證明類似于性質1，這里就不贅述了，有興趣的讀者可以自己嘗試去證明.這樣的話可以歸納出有心圓錐曲線的兩個共同的性質，這里僅以焦點在x軸上有心圓錐曲線作說明.

共同性質1 在一個有心圓錐曲線中，左右頂點分別是A1、A2，右準線與x軸的交點是P，過點P的直線l與這個圓錐曲線交于M、N兩點，過右焦點作x軸的垂線m,設直線A1M、A2N相交于點T，則點T在定直線m上.

共同性質2 在一個有心圓錐曲線中，左、右頂點分別是A1、A2，過右焦點F的直線l與這個圓錐曲線交于M、N兩點，設直線A1M、A2N相交于點T，則點T在右準線上.

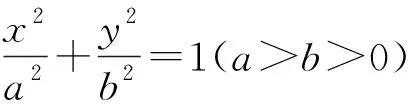
從廣義上來說，圓也是圓錐曲線，當平面只與圓錐面一側相交，且不過圓錐頂點，并與圓錐的對稱軸垂直，結果為圓 ，這樣也可以得到一個推廣.

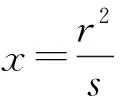
與有心二次曲線有所不同，拋物線與對稱軸只有一個交點，由射影幾何的知識知道：一個平面內兩條直線平行，那么這兩條直線就交于這兩條直線共有的無窮遠點.這樣的話可以大膽地猜想拋物線與對稱軸的另一個交點在拋物線對稱軸上的無窮遠處，經過小心地求證，于是就有了以下的性質.

圖3

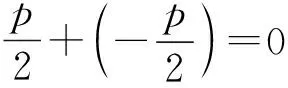
推廣4 在拋物線y2=2px(p>0)中，過x軸上一點S(s,0)，作直線l與拋物線交于M、N兩點，過點N作x軸的平行線m，直線OM與直線m相交于點T，則點T在定直線x=-s上.

在性質1中，當M、N兩點無限接近至重合時，這時M、N、T三點重合，直線l也就變成了橢圓的切線.性質3、5也可以進行類似的演繹，得到相似的結論.這樣可以得到圓錐曲線的一個公共性質,這里僅以焦點在x軸上的加以說明:在一個圓錐曲線中，焦點是F，其對應的準線與x軸的交點是P，過點F作x軸的垂線l，與這個圓錐曲線交于M、N兩點，則直線PM、PN與這個圓錐曲線相切.類似上面的三個推廣，這個性質也可以加推廣.

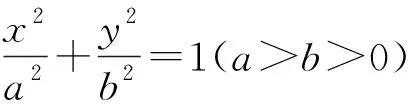
推廣7 在拋物線y2=2px(p>0)中，x軸上有兩點S(s,0)，T(t,0)(t>0)，s+t=0，過點T作x軸的垂線l，與拋物線交于M、N兩點，則直線SM、SN拋物線相切.

一道好的試題研究價值不應僅僅停留在解法上，還應該對試題本身做深入的探究，挖掘深層次的數學內涵，通過變式教學、引導學生探究、揭示數學本質[1].試題要發揮其最大功效，要進行拓展研究，挖掘試題的原理.馬波教授在《中學數學解題研究》中說到：開展解題研究，選擇適當的問題，從解題的某一個側面加以總結、概括、提升.教師在試題講解時應該注意創設合適的教學情境，啟發學生思考，大膽地假設、小心地求證，引導學生把握數學的本質.